Douce A.P. Thermodynamics of the Earth and Planets

Подождите немного. Документ загружается.

328 Phase equilibrium and phase diagrams

point of the pure substance, T

, as a function of the addition of “impurities” that lower the

activity of the substance in the melt phase, a

, in equilibrium with pure solid (a

constant

and equal to 1). Equation (6.49) is, however, completely general and applicable to any first-

order phase transition, even if some additional considerations are needed when applying it

to phase transitions involving a gas phase (next section).

We are also interested in how the activity ratio varies with pressure at constant

temperature. In this case it is straightforward to see that:

∂ ln K

∂P

=−



P,T

. (6.52)

If the pressure of the phase transition for pure A is P

, so that ln K

= 0, we get:

ln K

=−





P,T

dP. (6.53)

If the phases on both sides of the phase transition are condensed phases then it may be

acceptable as a first approximation to treat the volume change as a constant, in which case

we have:





=exp





(

−P

)



, (6.54)

where 

is the volume change associated with the phase transition of pure A at P

Separating ideal and excess contributions to activity and defining:

(

)

=exp





(

−P

)



(6.55)

we get:





=α

(

)





. (6.56)

The integrals in (6.48) and (6.53) can be refined by considering the temperature and

pressure dependencies of the enthalpy and volume changes of the phase transition. It is also

possible to write the freezing point depressions equation (6.49) as a function of the entropy

of the phase transition, something that we will do and justify in Chapter 10.

6.5.2 Phase transitions involving a gas at low pressure

If the phase transition involves a gas then it is necessary to define the standard state in such a

way that the energy contribution that arises from expansion of the gas is properly accounted

for. Here we will restrict the discussion to gases at pressures of order 1 bar or less, such that

the ideal gas approximation is acceptable. The phase transitions in question are boiling and

sublimation, that we will call in general vaporization, and their inverse, condensation, also

called deposition in the case that a gas condenses to a solid.

Recall that according to our labeling convention phase 2 is the high entropy and high

volume phase, so that it is the gas. Phase 1 can be either a liquid or a solid. We will choose

329 6.5 Chemical equilibrium

the standard states as pure gaseous A (phase 2) and pure A in phase 1 at 1 bar and the

temperature of the phase transition for the pure substance at 1 bar. With this definition

of standard states the activity of A in the gas is numerically equal to the partial pressure

of component A in the gas, p

(see equation (5.86)). The equilibrium constant in equation

(6.48) is therefore the ratio p

, and given our choice of standard states lnK

vanishes,

as before. We now write (6.49) as follows:





=−



(6.57)

For moderate temperature excursions relative to T

(the temperature of the phase transition

for pure A at 1 bar) 

can be considered to be constant. Equation (6.57) can then be

re-written as follows:

log





=a +

(6.58)

with a and b constants, and the natural logarithm conventionally replaced by decimal log-

arithm. This is the version of equation (6.49) that is widely used for phase transitions

involving a gas at low pressure. The partial pressure of gas species A, p

, in equilibrium

with a condensed phase in which the activity of species A is a

is called the vapor pressure

of A. We will return to this in Chapter 9, but it is important to understand what it means.

First, the definition of vapor is a gas in equilibrium with a condensed phase, solid or liq-

uid, of the same composition. If a condensed phase containing species A exists inside a

system whose volume is greater than that of the condensed phase, there is “empty space”

if you wish, then thermodynamic equilibrium requires that the chemical potential of A in

the “empty space” must be the same as the chemical potential of A in the condensed phase.

This means that there must be a vapor of A molecules in the “empty space”. The vapor

pressure of A is the partial pressure of A that makes the chemical potential of A in the vapor

(see equation (5.86)) equal to that of A in the condensed phase. If no other substances are

present then this partial pressure equals the total pressure on the system (equation (5.78)),

but at a given temperature the vapor pressure of A is fixed, regardless of the total pressure –

this is what equation (6.58) stands for. The relation is equally valid whether the condensed

phase is a liquid or a solid, although the vapor pressures of a solid and a liquid of the same

composition and at the same temperature are different, and so are the a and b parameters

in equation (6.58). Substances are said to be more volatile the higher their vapor pressure

is at a given temperature. The boiling point of a liquid is the temperature at which its vapor

pressure equals the total pressure, so that at least locally (at the liquid–gas interface) the gas

is made up exclusively of molecules with the same composition as the liquid. This concept

also works for solid–gas equilibrium, even if we don’t generally think of a boiling point for

solids.

The usefulness of equation (6.58) is that values of the parameters a and b are tabulated for

liquid–vapor and solid–vapor equilibria for many substances (see, for example, Lodders &

Fegley, 1998, Table 1.20), which makes calculation of vaporization equilibria very straight-

forward (see below). I emphasize, however, that (6.49) and (6.58) are the same equation. A

refinement of (6.58) that accounts for changes in 

with temperature is also widely used

and is known as the Antoine equation (Antoine equation parameters for many substances

can be found in the NIST Chemistry WebBook).

330 Phase equilibrium and phase diagrams

Suppose that we wish to use (6.58) to track changes in the equilibrium compositions

of gas and condensed phase with temperature, at a constant pressure P. We recall from

equation (5.78) that the mol fraction of species A in the gas phase is given by X

= p

/P.

Separating ideal and excess contributions to activity in the condensed phase we can rewrite

(6.58) as follows:





(

)

·γ

, (6.59)

where the exponential function in this case is:

(

)

=10





. (6.60)

Equation (6.58) can also be recast so as to track changes in phase composition with

pressure, at constant temperature. If we fix the temperature at some value of interest then

the right-hand side of (6.58), and hence α(T), is a constant. In particular, α(T) is equal to

the partial pressure of A in a gas in equilibrium with a condensed phase composed of pure

A at the temperature of interest. Let us call these values of partial pressure and activity

A,0

and a

A,0

= 1, respectively. From (6.58) it follows that for any other combination of

equilibrium values it must be:

A,0

. (6.61)

Let the total pressure on the system be P. Dividing (6.61)byP and separating the activity

coefficient in the condensed phase we get:





A,0

·γ

, (6.62)

which is the equivalent of 6.56 for vaporization reactions.

6.6 Discontinuous phase transitions in phases of

variable composition

We need to consider two distinct behaviors. In one instance there is complete miscibility

between two components, which we shall label A and B, in two phases, labeled 1 and 2,

separated by a discontinuous phase transition. By complete miscibility we mean that all

phase compositions between pure A and pure B are stable. Ideal solutions always exhibit

this behavior, as do non-ideal solutions above their critical point (Chapter 7).At the opposite

end of the spectrum is the case in which there is complete miscibility between A and B in

one of the phases, whereas on the other side of the phase transition A and B are present in

perfectly immiscible phases of constant composition, which we shall label a (= pure A)

andb(= pure B). Intermediate behaviors, in which limited miscibility exists on one or both

sides of a discontinuous phase transition, are common but will not be discussed here.

331 6.6 Discontinuous phase transitions

6.6.1 Complete miscibility in both phases

We discuss first the case in which the phase transition occurs between two phases in both

of which the two components, A and B, are fully miscible. We will abide by the following

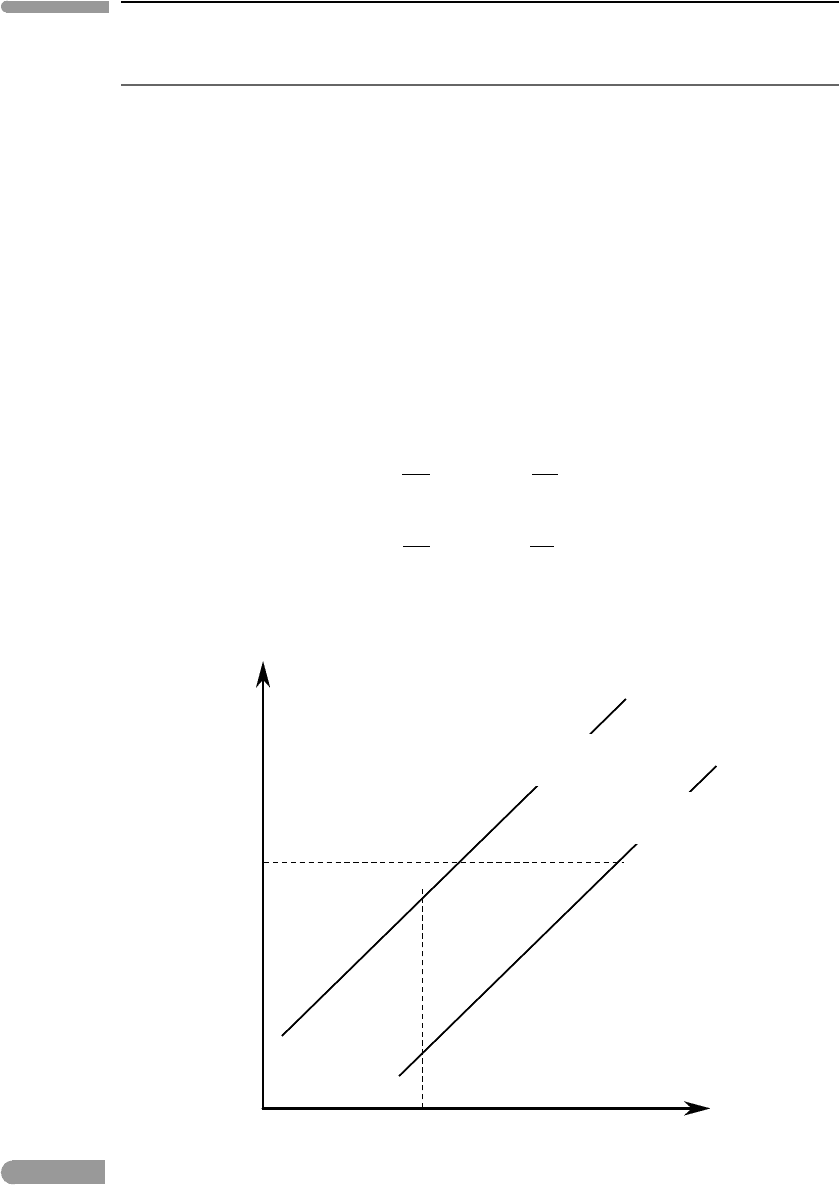
conventions regarding phases and components (see Fig. 6.17). First, phase 2 has higher

entropy and volume than phase 1. Thus, phase 2 occurs on the high temperature and low

pressure side of the phase transition. Second, the transitions for the pure phases occur at

different temperatures and pressures, such that, at constant pressure T

and at constant

temperature P

. You can think of component B as being more refractory and less

volatile than A, but these definitions are not entirely clear if applied, for example, to a

solid–solid phase transition, or to the effect of pressure on a melting reaction.

Let us look first at the behavior of the phase transition at constant pressure. For a given

temperature we have two versions of equations (6.50)or(6.59), depending on whether only

condensed phases or a gas phase is present:





=α

(

)









=β

(

)





(6.63)

Phase 2

Phase 1

Phase transition

for pure A

Phase transition

for pure B

Fig. 6.17

Labeling convention for phases and components in binary phase diagrams with phases of variable composition – see

text.

332 Phase equilibrium and phase diagrams

or, if a gas is present:





(

)

·γ





(

)

·γ

(6.64)

where I have used β(T ) to represent the exponential function (6.51)or(6.60) for phase B.

In addition, because the system is binary, we have the conditions:

=1. (6.65)

The activity coefficients are functions of composition and, perhaps, temperature. Thus, at

constant temperature we have a system of four equations that we can solve for the four

mol fractions, i.e. for the compositions of the two phases at equilibrium along the phase

transition.The general solution can be quite messy because of the compositional dependency

of activity coefficients, and must generally be obtained numerically. However, if the phases

can be considered to be ideal mixtures, or if the departures from ideality are comparable

in the two phases so that the ratio of activity coefficients in (6.63) is of order 1, then the

general solutions are very simple. For phase transitions among condensed phases:

(

)

−1

(

)

−α

(

)

=α

(

)

(

)

−1

(

)

−α

(

)

(6.66)

and for vaporization transitions:

(

)

−P

(

)

−α

(

)

(

)

(

)

−P

(

)

−α

(

)

. (6.67)

The distribution of component B follows trivially from (6.65).

Note some important properties of these equations. First, for T>T

both α(T)

(or α(T )/p) and β(T) (or β(T )/p) are greater than 1. If the activity coefficients are unity then

this is impossible by (6.63)or(6.64). The condition T

>T leads to another impossible

result. Thus, the only feasible solutions are in the interval T

≥T ≥T

. This means that the

phase transition for any composition intermediate between A and B occurs at a temperature

that is intermediate between the temperatures at which the two end-members undergo the

phase transition. Second, from the condition T

≥ T ≥ T

it follows that X

> X

and

> X

. The low-temperature phase, 1, is enriched in the more refractory component, B,

relative to the high temperature phase, and conversely for the less refractory component,

A. Note that these conclusions are not necessarily valid if excess mixing properties are not

negligible.

The solution for the behavior of the phase transition with pressure at constant temperature

is analogous. Assuming that activity coefficients can be neglected we obtain, for condensed

333 6.6 Discontinuous phase transitions

phases:

(

)

−1

(

)

−α

(

)

=α

(

)

(

)

−1

(

)

−α

(

)

(6.68)

and for vaporization:

B,0

−P

B,0

−p

A,0

B,0

−P

B,0

−p

A,0

. (6.69)

In this case we find that, if activity coefficients can be neglected, then the physical solutions

are in the interval P

≤P ≤ P

, and from this condition we find that it must be X

> X

and X

> X

. The low-pressure phase, 2, is enriched in the more volatile component,

relative to the high-pressure phase, and conversely for the less volatile component, B (see

also Fig. 6.17).

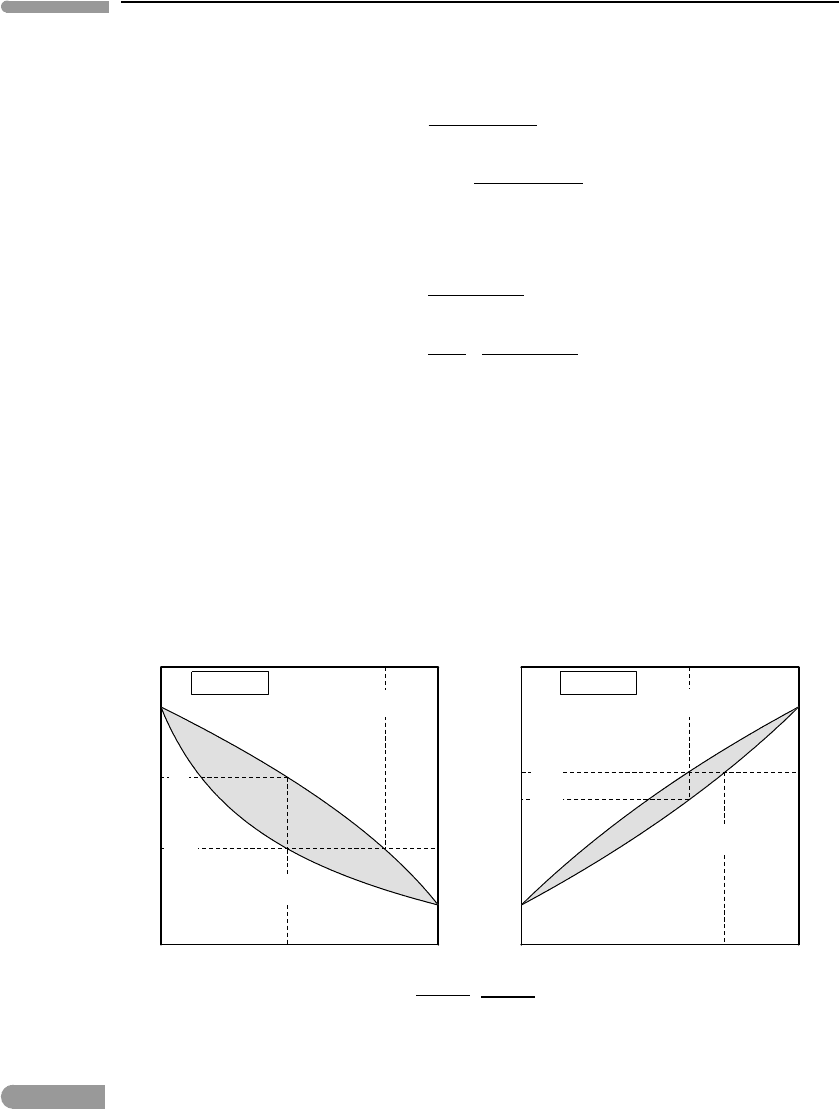
Figure 6.18 shows the topology of the phase diagrams calculated with these equations.

Each diagram consists of two curves that map the equilibrium compositions of phase 1 and

phase 2, expressed as a function of the mol fraction of component A. For example, at T

, phase 1 of composition X

is in equilibrium with phase 2 of composition X

X (A)

X(A)

Phase 1

Phase 2

Phase 1

solid

liquid

Phase 2

solid

liquid

gas

(i) (ii)

P = constant

T = constant

1 1

Fig. 6.18

T–X and P–X diagrams for phase transitions between two binary phases, in both of which there is complete

miscibility between components A and B. Phase 2 has higher entropy and molar volume than phase 1 (possible

combinations of phases are listed at the bottom of the ﬁgure). The two phases exist at equilibrium inside the shaded

regions. The compositions of the coexisting phases are given by the intersections of the T or P coordinate with the

respective bounding curves.

334 Phase equilibrium and phase diagrams

Phase 1 is stable at lower T and higher P than phase 2. A one-phase assemblage in a

binary system has three degrees of freedom, which in this case we choose as P, T and a

chemical potential that is represented by a compositional variable, X(A). Pressure is fixed in

diagram (i) and temperature is fixed in diagram (ii), so each of the one-phase assemblages

is stable over a two-dimensional region (T–X or P–X, respectively) in the phase diagrams.

Each of these regions terminates at a curve (calculated with the corresponding equation

for X

or X

) that represents the location of the phase transition. Inside the shaded area

bound by the two curves the two phases are stable, so that there are two degrees of freedom.

In diagram (i) these are pressure, which is fixed, and either temperature or composition,

whereas in diagram (ii) they are temperature (fixed) and either pressure or composition. At

a given temperature in (i), say T

, and the pressure chosen to construct the diagram, the

compositions of the coexisting phases, X

and X

, and hence all the chemical potentials,

are determined by the solutions to the systems of equations that we derived above, with no

possibility of arbitrarily choosing the value of any other variable. For any combination of

bulk composition and temperature in diagram (i), or bulk composition and pressure in (ii),

that plots inside the shaded regions there are two phases at equilibrium, whose compositions

are given by the intersections of the two bounding curves with the temperature or pressure

coordinate. The two phases can exist at equilibrium at T

,orP

, only if the bulk composition

of the system lies between X

and X

. If the system is richer in B relative to this interval

then only phase 1 is stable at these conditions, and conversely only phase 2 is stable in a

system whose bulk composition is richer in A than X

The phase transition in the binary system occurs over a divariant region, rather than along

a univariant curve as in the case of a one-component system. For example, as temperature

rises or pressure falls, phase 1 of composition X

will begin to undergo the transition to

phase 2 at T

,orP

, respectively, at which conditions phase 2 of composition X

will form.

In a closed system the two phases may remain at equilibrium, while changing composition,

until T

,orP

, are reached, at which point phase 2 will have attained composition X

Further increase of temperature or decrease of pressure will cause phase 1 to disappear.

More interesting behaviors become possible in open systems. For instance, if phase 2 is lost

from the system then the bulk composition shifts in the direction of component B, and the

phase transition will extend beyond T

,orP

, conceivably all the way to the values for the

univariant equilibrium in the pure B system, T

or P

The type of phase diagram shown in Fig. 6.18(i), and the different behaviors that are

possible depending on whether the system is closed or open, are of course familiar to geolo-

gists from elementary igneous petrology. They are commonly exemplified by the olivine or

plagioclase melting loops. If the phase diagram corresponds to a melting reaction, then the

curve that maps the upper thermal stability of the solid phase is called the solidus, whereas

the lower thermal stability of the melt is mapped by the liquidus. Note that the solidus and

the liquidus coincide for the two degenerate end-member systems. I wish to present these

results in a different light from that commonly associated with igneous petrology, empha-

sizing their generality and in particular the following three points. First, melting is only

one of the possible types of discontinuous phase transitions involving phases of variable

composition. The thermodynamic relations and topology of the resulting phase diagrams

are the same for other discontinuous phase transitions. Second, temperature has no special

status as an intensive variable. Phase compositions at the transition can also be tracked as

a function of pressure, if it is more convenient. Third, the topology of the phase diagram is

determined by the solutions to sets of equations such as (6.63) and (6.65), (6.64) and (6.65),

and so on. All that these equations require is that the curve that maps the composition of

335 6.6 Discontinuous phase transitions

the high-entropy, or high-volume, phase be located at higher temperature, or lower pres-

sure, than the curve that maps the composition of the low-entropy or low-volume phase.

The equations per se do not determine neither the separation between the curves nor their

curvature. These quantities depend on the relative values of temperature, pressure, enthalpy

change and volume change of the phase transitions for the pure end-member phases, as

we shall see in the following examples. Also important are the excess mixing properties of

the two phases, which we have ignored in this discussion. It is generally far from trivial to

account for these in calculations and we shall not attempt it here. Many phase diagrams are,

however, constructed empirically, so that they conflate all of these effects from experimental

measurements.

Worked Example 6.8 Crystallization of planetary mantles and cores

At temperatures close to their melting points, olivine forms a complete solid solution

between the Fe and Mg end-members, fayalite and forsterite, and so do Fe and Ni met-

als. Solid–liquid equilibria in these two systems constitute very simplified models for the

crystallization of the mantles and cores of the terrestrial planets. These simple models cap-

ture some of the important physicochemical aspects of those processes, however.Assuming

that excess mixing properties can be ignored all that we need in order to construct phase

diagrams for melting of olivine or Fe–Ni alloys using equations (6.66) are the melting points

and enthalpies of fusion of each of the end-members – see equation (6.49). The required

values are: T

=2163 K, T

=1490 K, 

=71.1 kJ mol

−1

, 

=92.2 kJ mol

−1

and T

=1809 K, T

=1726 K, 

=14.2 kJ mol

−1

, 

=18.2 kJ mol

−1

. With

these data we calculate α(T) and β(T) with equation (6.51), and the compositions of the

coexisting phases, for a series of temperatures, T

≥T ≥T

(a spreadsheet program such

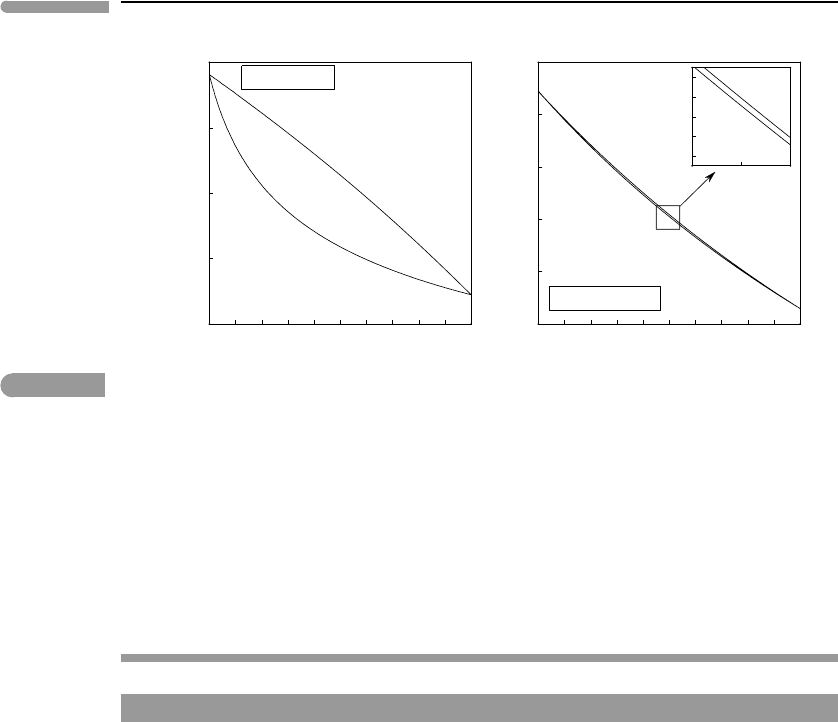
as QuattroPro will do this effortlessly). The resulting phase diagrams (at 1 bar pressure)

are shown in Fig. 6.19. If you compare the olivine phase diagram in the figure with the one

shown in igneous petrology textbooks you will notice that they differ. This is so because

the diagram shown in textbooks is constructed from experimental results, and thus includes

the effects of non-ideal mixing in olivine and melt. That diagram is the correct one, but the

simplified version shown in Fig. 6.19 will do for our purposes.

There is a striking difference between the olivine and metal phase diagrams. First, the

solidus and liquidus curves have curvatures of opposite signs in the olivine phase diagram,

whereas both have positive curvature in the metal phase diagram. Second, and more impor-

tantly, the curves for olivine are widely separated, whereas they almost coincide with one

another in the metal diagram (see inset). Melting, or crystallization, strongly fractionates

olivine compositions, but that is not the case for Fe–Ni metal alloys. The different behaviors

are rooted in the different enthalpies (and entropies) of fusion of the two systems, which

are about five times greater in the silicates compared to the metals (see also Chapter 10).

Equation (6.49) shows that, for a given temperature, the ratio between the activity of a com-

ponent in phase 1 relative to its activity in phase 2 varies exponentially with the enthalpy

of transition.

We can think of two ways in which these contrasting behaviors may have affected the

evolution of terrestrial planets. First, mantle crystallization from a magma ocean of olivine

composition produces olivine crystals considerably richer in Mg than the liquid. If the

densities of the solid and liquid phases differ significantly then the two phases would

become separated and crystallization would take place in an open system. The residual

liquids would become progressively enriched in Fe, resulting in a planetary mantle with

336 Phase equilibrium and phase diagrams

0 0.2 0.4 0.6 0.8 1

1400

1600

1800

2000

2200

X(Fa)

T (K)

0 0.2 0.4 0.6 0.8 1

1720

1740

1760

1780

1800

1820

X (Ni)

T (K)

olivine

melt

solid metal

0.45 0.5 0.55

1755

1760

1765

liquid metal

liquid

metal

solid

metal

Olivine at 1 bar

Fe-Ni alloy at 1 bar

olivine

melt

Fig. 6.19 Schematic melting relations for olivine solid solution and Fe–Ni alloy, calculated with the simplifying assumption that

the solid and liquid phases are ideal solutions. The enthalpy of fusion of the silicates is ∼5 times greater than that of

the metal, causing the wider separation between the solidus and liquidus curves. A section of the metal phase

diagram is magniﬁed, showing the extent of solid–liquid fractionation.

primary compositional stratification. Such stratification is less likely to develop in metallic

cores, given that the Fe–Ni alloy that crystallizes from a molten metal mixture has virtually

the same composition as the liquid. Second, in a crystallizing silicate mantle there is a wide

temperature interval over which solid and liquid coexist, which may lead to a sizable depth

interval over which the melt fraction varies between 1 and 0. In contrast, solidification of

a metal core can be expected to take place along a sharp front.

Worked Example 6.9 Hydrocarbons in Titan’s atmosphere–hydrosphere cycle

Titan’s atmosphere is composed predominantly of nitrogen, but it has been known for a long

time that non-trivial amounts of hydrocarbons are also present. The Cassini–Huyghens mis-

sion has revealed remarkably Earth-like landforms, including dendritic drainage networks,

lakes and dry lake beds. It is thought that Titan’s rocky surface consists chiefly of water ice,

and that surface liquids are hydrocarbons. Hydrocarbons in Titan play a role comparable to

that of water in the terrestrial atmosphere. The dominant hydrocarbon species present in the

atmosphere is methane, accompanied by lesser amounts of ethane. The two hydrocarbons

are fully miscible in both the liquid and gas phases. Condensation of atmospheric gases and

evaporation of liquid hydrocarbons from lakes should lead to methane–ethane fractionation

in Titan’s climate cycle.

Titan’s surface atmospheric pressure is about 1.5 bar, with a hydrocarbon mol fraction of

∼0.05, so that the partial pressure of hydrocarbons in Titan’s atmosphere is ∼75 mbar. Using

equation (6.58) and a and b parameters from Lodders and Fegley (1998) and NISTChemistry

WebBook we find that the temperature at which the end-members attain a saturation vapor

pressure of 75 mbar are 88 K for methane and 147 K for ethane. Given that the average

surface temperature is ∼95 K, there must exist a range of bulk compositions over which

liquid and vapor coexist.

We can use equations (6.67) to calculate the compositions of the coexisting phases at

P = 75 mbar. This calculation assumes that the sum of the partial pressures of the two

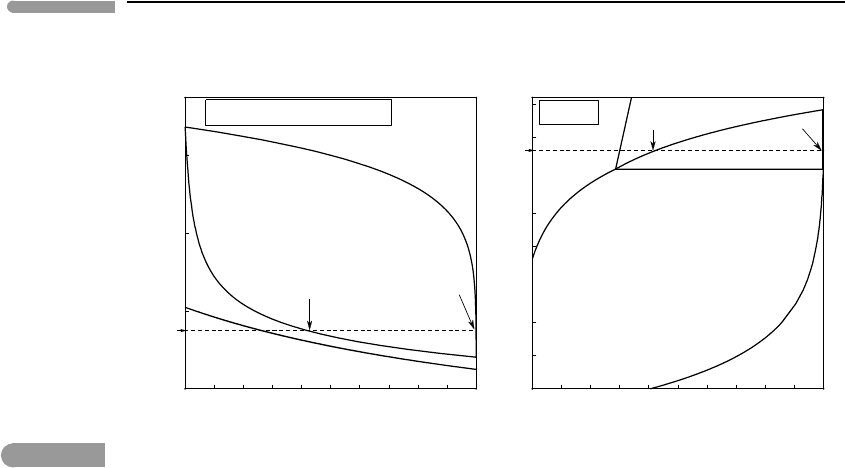
337 6.6 Discontinuous phase transitions

0 0.2 0.4 0.6 0.8 1

100

120

140

XCH

/(XCH

+XC

)

T(K)

liquid

vapor

hydrocarbons

=0.05P

atm

= 75 mbar

lake

air

Hydrocarbons in Titan’s atmosphere and hydrosphere

solid

0 0.2 0.4 0.6 0.8 1

100

200

XCH

/(XCH

+XC

)

hydrocarbons

(mbar )

liquid + vapor

95 K

vapor

liquid

T = 95K

liquid + vapor

solid

75 mbar

solid + vapor

lake

air

Fig. 6.20 Methane–ethane liquid–vapor equilibrium at the conditions of Titan’s surface (95 K and 1.5 bar), assuming a

constant hydrocarbon partial pressure of 75 mbar. Lakes are likely to be strongly enriched in ethane relative to

methane, compared to atmosphere. The solid–vapor section of the P–X diagram is only schematic, as the saturation

vapor pressure of ethane over solid ethane is not well known (see text). Note logarithmic scale on pressure axis.

hydrocarbons does not change with temperature, which is a somewhat artificial constraint

that we will address later. As in the previous example, we calculate α(T) and β(T) for

temperatures in the range 88–147 K, but in this case with equation (6.60). The resulting

phase diagram is shown in the left panel of Fig. 6.20. Because hydrocarbons are not the

only components present in the gas phase, the horizontal coordinate in the phase diagram

is not the absolute mol fraction of methane, but rather the ratio of mols of methane to mols

of methane + ethane, which are the two species that contribute to the partial pressure of

hydrocarbons in our model.

At the conditions of Titan’s surface methane–ethane mixtures with a molar proportion of

methane greater than ∼0.4 exist as liquids at equilibrium with atmospheric hydrocarbons.

One can therefore expect evaporation from hydrocarbon lakes and hydrocarbon rain. There

is, however, strong fractionation between the two phases. Hydrocarbon vapor is almost pure

methane, but the lakes are about 60% ethane. Note that although it is possible to predict

the composition of Titan’s lakes from hydrocarbon partial pressure in the atmosphere and

temperature, it is not possible to derive a bulk methane–ethane ratio from these data alone.

The bulk composition can lie anywhere between about 60% ethane and almost pure methane,

and would be reflected in the relative masses of liquid and gaseous hydrocarbons.

Some other issues need to be addressed. First, is there a chance that hydrocarbons will

solidify on Titan’surface? The melting points of pure methane and ethane are 85 and 101 K,

and the enthalpies of fusion are 0.94 and 0.58 kJ mol

−1

, respectively. Assuming that they

mix ideally in the solid state (this is probably incorrect, but it is OK for this discussion,

and is explored further in the end-of-chapter exercises), we calculate a binary melting

loop as in Worked Example 6.8. The melting loop is also shown in the left panel of Fig.

6.20. Given the very low enthalpies of fusion the solidus and liquidus curves are virtually

indistinguishable from one another. For the compositional interval of possible liquid–vapor

equilibria the freezing curve is below Titan’s average surface temperature. Mixtures with

more than about 70% ethane would freeze, however.