Douce A.P. Thermodynamics of the Earth and Planets
Подождите немного. Документ загружается.

388 Equations of state for solids
T
P
(0,T
0
) (0,T)
(P
0
,T
0
)
cold isothermal compression
isobaric expansion
isobaric expansion
(P,T)
P
th
isochoric heating
hot isothermal compression
T
V
V(0,T
0
)
V(0,T )
V(P
0
,T
0
)
V(P,T )
hot isothermal compression
isochoric heating
cold
isothermal compression
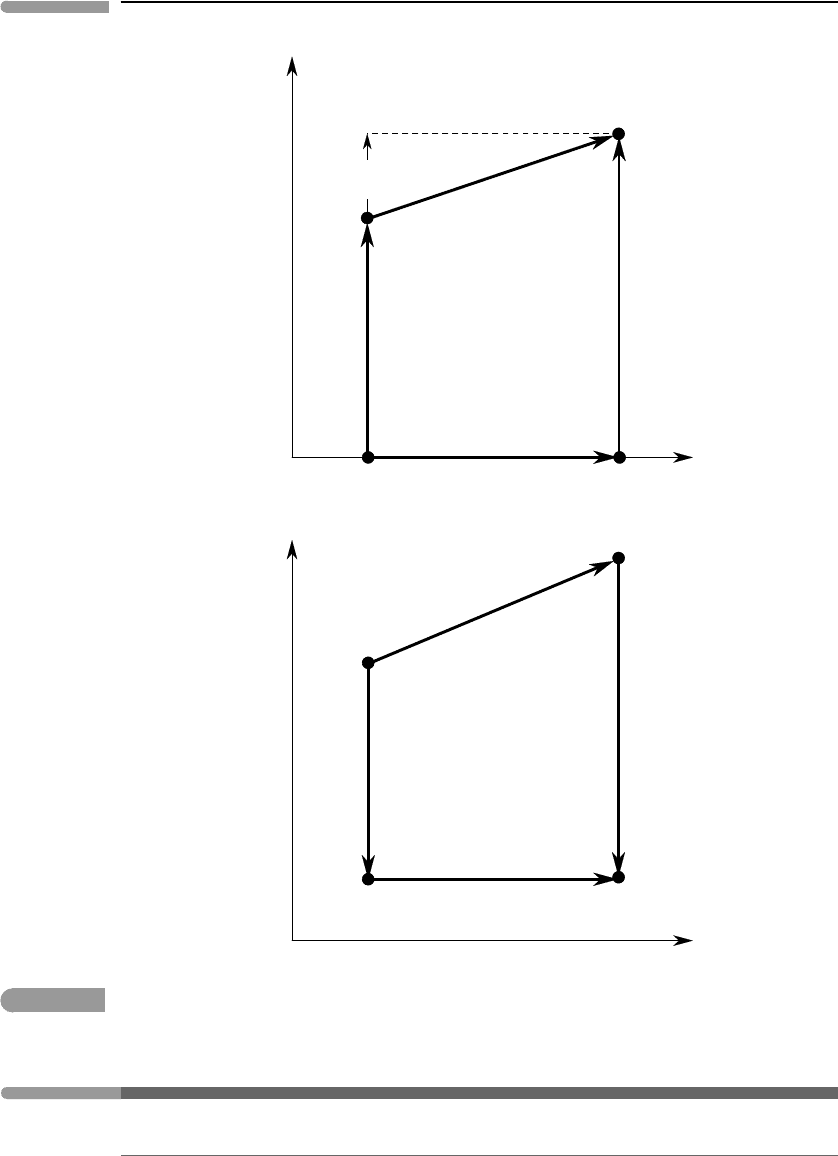
Fig. 8.1
Two ways of calculating V =V(P,T) or P = P(V,T). An isothermal equation of state is needed in both cases.
8.2 Macroscopic equations of state
8.2.1 The Murnaghan isothermal EOS
This equation of state follows directly from thermodynamic identities, even if it was origi-
nally derived by Murnaghan (1937) from finite strain considerations. We begin by recalling

389 8.2 Macroscopic equations of state
the definition of the isothermal bulk modulus, equation (1.21):
K
T
=−V
∂P
∂V
T
. (8.3)
Integrating (8.3) at constant T we get:
ln
V
P ,T
V
0,T
=−
P
0
dP
K
T
(8.4)
where we use 0 as the lower integration limit because we integrate from “zero pressure”.
The integral on the right-hand side of (8.4) would be very easy to solve if the isothermal
bulk modulus were constant, which would require that all third derivatives of the Gibbs
free energy vanish. This is in general not the case, however. Rather, the isothermal bulk
modulus is a function of both temperature and pressure. Because equation (8.4) is integrated
at constant temperature, however, K
T
can be treated as a function of pressure only, at a
constant temperature T. The simplest possible assumption now is to make K
T
a linear
function of P so that, using K
T
for the first pressure derivative of K
T
, we write:
K
T
=
∂K
T
∂P
T
=constant. (8.5)
This approximation, which is equivalent to assuming that the third pressure derivative of
the Gibbs free energy does not vanish but the fourth and higher derivatives do, leads to
what is known as the Murnaghan equation of state.IfweuseK
0,T
to symbolize the bulk
modulus at zero pressure and temperature T, then integration of (8.5) yields:
K
T
=K
0,T
+K
T
P . (8.6)
Substituting in (8.4):
ln
V
P ,T
V
0,T
=−
P
0
dP
K
0,T
+K
T
P
. (8.7)
Making the substitution u=K
0,T
+K
T
P, this integrates easily to:
ln
V
P ,T
V
0,T
=−
1
K
T
ln
K
0,T
+K
T
P
K
0,T
(8.8)
or:
V
P ,T
=V
0,T
1 +
K
T
P
K
0,T
−
1
K
T
, (8.9)
which is the volume-explicit form of Murnaghan’s equation of state. The temperature of
interest, T, can be any value that is convenient. If T = T
0
then we substitute V
0
for V
0,T
in (8.9) – this is a notation issue, but it is important to keep it straight for consistency with
what follows. The Murnaghan EOS works well up to pressures of the order of 200 kbar.
More accurate representations of volume are needed at higher pressure.
To apply the Murnaghan EOS (equation (8.9)) or Birch–Murnahgan EOS (see below) at
any arbitrary temperature we need to account for thermal expansion at zero pressure, so as
to calculate V
0,T
, and we need the values of the bulk modulus and its pressure derivative.
Before we proceed with other isothermal EOS we discuss how each of these steps is handled
for solid materials.

390 Equations of state for solids
8.2.2 Thermal expansion at zero pressure
Recalling the definition of the coefficient of thermal expansion, equation (1.66):
α =
1
V
∂V
∂T
P
(8.10)
we see that volume at zero pressure and the temperature of interest is given by:
V
0,T
=V
0
exp
T
T
0
α dT
, (8.11)
where V
0
is the volume at zero pressure and the reference temperature T
0
(generally, 298 K).
Evaluating 8.11 requires a function α = α(T ).
The behavior of the coefficient of thermal expansion with temperature parallels that of
heat capacity. In Section 1.14.3 we saw that heat capacity increases strongly with T at low
temperature, and that the T dependency becomes weaker as the Debye temperature of the
material θ
D
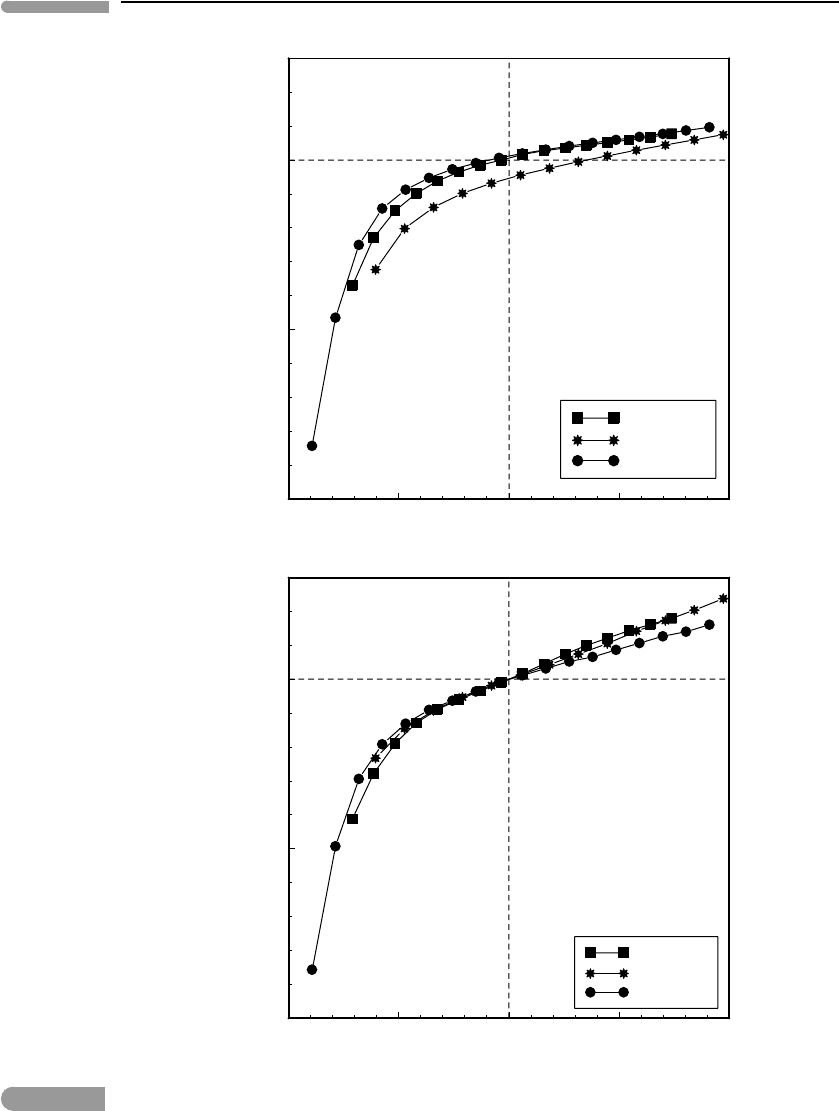
is approached. Figure 8.2a shows this relationship, plotted as non-dimensional
heat capacity vs. non-dimensional temperature for three minerals, periclase, corundum
and forsterite, for which the values of θ
D
are approximately 940 K, 1040 K and 760 K,
respectively (data from Anderson et al., 1992). In the graph I have normalized temperature
to θ
D
and heat capacity to the Dulong and Petit values (Section 1.1.4.3) for each of the
three minerals. This procedure makes the regularity of the behavior hinted at in Fig. 1.15
strikingly clear. What is perhaps even more remarkable is that thermal expansion behaves in
essentially the same way. This is shown in Fig. 8.2b, in which I normalized the coefficients
of thermal expansion for the same three minerals to the values measured at or close to the
Debye temperature, symbolized by α
θ
D
. The reason for the similar behavior arises from
the fact that heat capacity and thermal expansion are both macroscopic manifestations of
changes in atomic vibration modes. The importance of the trends shown in Fig. 8.2 for our
present purposes is that they suggest that we can represent thermal expansion coefficients
with polynomial functions similar to the ones used to express heat capacity as a function
of temperature. There appears to be less common ground regarding the actual function that
should be used to represent thermal expansion than there is for heat capacity, though. For
instance, Berman (1988) and Chatterjee et al. (1998) propose two-parameter polynomials,
Saxena et al. (1993) a polynomial with four parameters, and Holland and Powell (1998)a
single-parameter equation.
8.2.3 Bulk modulus at zero pressure
The second parameter required for the “hot isothermal compression” approach is the bulk
modulus at zero pressure and the temperature of interest: K
0,T
. Measurements show that
the bulk modulus of minerals decreases linearly with increasing temperature (i.e., minerals
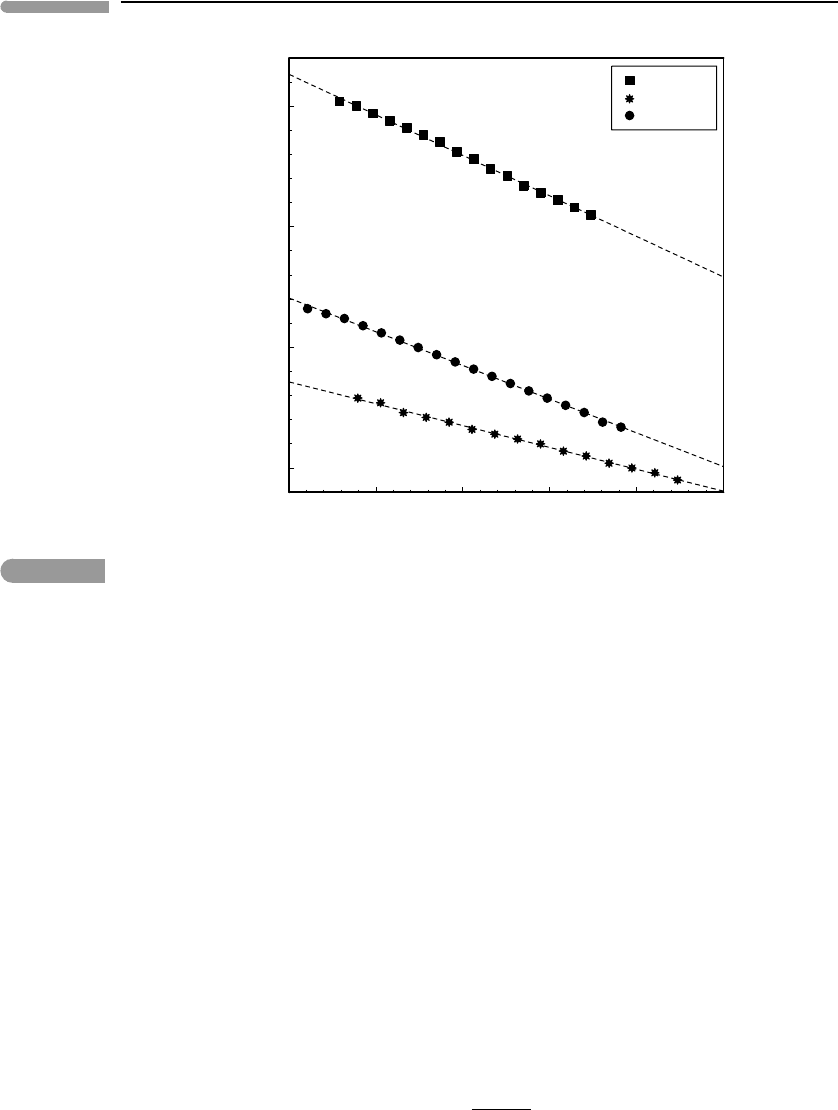
become weaker with increasing temperature). This is exemplified in Fig. 8.3, which is drawn
for the same minerals shown in Fig. 8.2 (data from Anderson et al., 1992). The behavior of
bulk modulus with temperature is quite regular and, in contrast to heat capacity and thermal
expansion, does not appear to be significantly affected by whether the mineral is above
or below its Debye temperature. One could infer from Fig. 8.3 that our problem is easily
solved, as one would just need to obtain data such as those in this figure for all minerals,
and values of K
0,T
would be readily available for any temperature. Alas, this is not the
391 8.2 Macroscopic equations of state
0 0.5 1 1.5
2
0
0.5
1
C
P
/C
P
,
Dulong and Petit
Al
2
O
3
Forsterite
MgO
0 0.5 1
T/θ
D
T/θ
D
1.5
2
0
0.5
α/α
θ
D
1
Al
2
O
3
Forsterite
MgO
(a)
(b)
Fig. 8.2
Non-dimensional heat capacities (top) and thermal expansion coefficients (bottom) for Al
2
O
3
,Mg
2
SiO
4
and MgO
(data from Anderson et al., 1992), plotted against non-dimensional temperature. Heat capacities are normalized to
the Dulong and Petit values (Section 1.14.3). Thermal expansion coefficients are normalized to the values measured
at, or close to, the Debye temperature, θ
D
.
392 Equations of state for solids
0 0.5 1 1.5
T/θ
D
K
0, T
(GPa)
22.
5
100
150
200
250
Al
2
O
3
Forsterite
MgO
Fig. 8.3
Variation of zero-pressure isothermal bulk modulus with non-dimensional temperature. Data from Anderson et al.
(1992).
case, because constructing curves such as those in this figure requires measurements of
the bulk modulus at high temperature and atmospheric pressure, and this is experimentally
rather difficult. What can be measured more easily is thermal expansion at high temperature
and atmospheric pressure (these are the data shown in Fig. 8.2b) and compressibility (the
inverse of bulk modulus) as a function of pressure at room temperature. We therefore need a
thermodynamic relation that allows us to calculate bulk modulus at high temperature starting
from the measurements that are easier to make. This is a topic of immense importance in
the study of planetary interiors, as it is relevant not only to phase equilibrium but also to the
determination of the elastic constants that need to be known in order to interpret seismic
data. We can only cover the most basic aspects in this book. Two excellent references for
in-depth study are the books by D. L. Anderson (1989) and O. L. Anderson (1995).
We begin from the observation that, if both volume and bulk modulus vary regularly with
temperature at zero pressure (as suggested by Figs. 8.2b and 8.3), then the same must be
true of the relationship between the two variables at constant pressure. Figure 8.4 shows
that graphs of ln(K
0,T
) vs. ln(V ) at zero pressure for the same three minerals as before are
straight lines, and, moreover, that they all have approximately the same slope, ≈−5. This
observation suggests that the parameter δ
T
, defined as follows, may be significant:
δ
T
≡−
∂ ln K
T
∂ ln V
P
, (8.12)
where δ
T
is called the isothermal Anderson–Grüneisen parameter, and provides the
crucial link that makes the calculation of K
0,T
possible. From the chain rule of

393 8.2 Macroscopic equations of state
0 0.5 1 1.5
6.8
7
7.2
7.4
7.6
7.8
ln V (Jbar
–1
)
ln K
0,T
(kbar)
Al
2
O
3
Forsterite
MgO
Fig. 8.4
Variation of zero-pressure isothermal bulk modulus with volume. Temperature varies as in Fig. 8.3 (note different
units for K
0,T
). Data from Anderson et al. (1992).
differentiation we get:
∂ ln K
T
∂ ln V
P
=
∂ ln K
T
∂K
T
∂K
T
∂V
P
∂V
∂ ln V
=
1
K
T
∂K
T
∂V
P
V (8.13)
or:
δ
T
=−
V
K
T
∂K
T
∂V
P
. (8.14)
Also from the chain rule, and using the definition of the coefficient of thermal expansion,
(8.10):
∂K
T
∂V
P
=
∂K
T
∂T
P
∂T
∂V
P
=
1
αV
∂K
T
∂T
P
. (8.15)
From (8.14) and (8.15) it follows that:
∂K
T
∂T
P
=−αK
T
δ
T
. (8.16)
Now, (∂K
T
/∂T)
P
is the slope of the lines in Fig. 8.3. If we can assume that the behavior
of these three crystalline solids is true of all minerals, then (∂K
T
/∂T)
P
is a charac-
teristic constant for each mineral. We can approximate this constant by substituting in
equation (8.16) values of α and K
T
measured at a single temperature, and some charac-
teristic value of δ
T
. In particular, we can use the values at the reference state, α
0
and K
0
.
Integrating equation (8.16) and taking the reference state at 298 K we get the following

394 Equations of state for solids
equation for K
0,T
:
K
0,T
=K
0
[
1 −δ
T
α
0
(
T −298
)
]
. (8.17)
If δ
T
can be assumed to be a constant then this equation is general, as it follows from ther-
modynamic identities and not from any specific material properties. The room-temperature
values α
0
and K
0
are known for most minerals, but there is the difficulty of the parameter
δ
T
. Treating it as a constant is a convenient assumption but is not strictly true. In fact, the
Anderson-Grüneisen parameter does vary with temperature, although not strongly, and it
is also somewhat different for different minerals. For most minerals at terrestrial mantle
temperatures δ
T
varies within a factor of 2, in the range 4–8.
8.2.4 Pressure derivative of the bulk modulus
The pressure derivative of the bulk modulus, K
, is a dimensionless number that is generally
within the range 3.5–7 and close to, but smaller than, δ
T
. If a measured value of K
exists for
the mineral of interest then it can be used in an EOS. It will become important to understand
where the relationship between K
and δ
T
comes from, however. We begin by forming the
product αK
T
. Using the definitions of α and K
T
, and identity (1.3.19)inBox1.3, we find
that:
αK
T
=−
∂V
∂T
P
∂P
∂V
T
=
∂P
∂T
V
. (8.18)
Thus, the product of the two material properties α and K
T
gives the change in pressure with
temperature, at constant volume. This is the thermal pressure that we discussed in Section
8.1 (see Fig. 8.1) and to which we will return later. For now we note that it is an empirical
observation that for solids at high temperature, which roughly means above their Debye
temperature, αK
T
is a very weak function of P and T (see, for example, Anderson et al.,
1992). This is of interest for our present discussion. Taking the pressure derivative of αK
T
at constant temperature we get:
∂
(
αK
T
)
∂P
T
=K
T
∂α
∂P
T
+α
∂K
T
∂P
T
. (8.19)
It is straightforward to prove that (Exercise 8.2):
∂α
∂P
T
=
1
K
T
2
∂K
T
∂T
P
. (8.20)
Substituting in (8.19) and using (8.5) and (8.16), we get:
∂
(
αK
T
)
∂P
T
=
1
K
T
∂K
T
∂T
P
+αK
=α
K
−δ
T
. (8.21)
If αK
T
can be considered to be constant at high temperature then its pressure derivative
vanishes. In the absence of measured values for one or the other of the parameters, it is
therefore often assumed that:
K
≈δ
T
(8.22)
This remains an approximation, generally valid at high temperature, but it is no substitute
for measured values. When the latter do exist it is found that δ
T
≥K
.

395 8.2 Macroscopic equations of state
Worked Example 8.1 Some mineral reactions in the Earth’s upper mantle
Let us look at the effect of ignoring the compressibility and thermal expansion of solid
phases on the calculated location of some important phase boundaries in the Earth’s upper
mantle. As in other examples focusing on crustal and upper mantle conditions, and also
because their data set is large, allowing for the formulation of many different examples,
I will use standard state thermodynamic properties from Holland and Powell (1998). We
must therefore use their treatment for compressibility and thermal expansion, which is
based on the isothermal Murnaghan EOS. The Maple implementation of the procedures
discussed here is given in Software Box 8.1.
Software Box 8.1 Calculation of Gibbs free energy of solid phases at high pressure with
Murnaghan equation of state
Software Box 7.2 describes the procedures Peq and Teq in worksheet
th_template_4.mw. These procedures include a call to the procedure vdp, that
is also included in th_template_4.mw.
Procedure vdp calculates the total contribution of pressure to the Gibbs free
energy of reaction by calling function vdp_hp, which is included in the package
th_shomate.mw. The function vdp_hp calculates the integral of the Murnaghan
equation of state for a phase (equation (8.24)), using Holland and Powell’s data and for-
malism to calculate thermal expansion at 1 bar and the value of the bulk modulus at the
temperature of interest. An examination of the lines of code in vdp_hp and comparison
with the discussion in Section 8.2 and Worked Example 8.1 is self-explanatory.
Procedure vdp calls vdp_hp for each phase in the reaction, multiplies the Gibbs
free energy term by the stoichiometric coefficient, and adds up the contributions of all
of the phases in the reaction. In Peq and Teq this Gibbs free energy is then added to the
Gibbs free energy of reaction at 1 bar, calculated with DGT_sh, and any contribution
from order–disorder, calculated with Gord, and the condition
r
G = 0 is then solved
for iteratively, as discussed in Software Box 7.2.
Peq and Teq include all of the calculations necessary to calculate the equilibrium
of a solid assemblage in which all phases are in their standard states, with Holland and
Powell’s data base. This includes the heat capacity integral, thermal expansion contribu-
tion, Murnaghan EOS pressure integral and Landau potential contribution. Calculation
of equilibrium among solid solutions is handled by adding energetic contributions from
non-unit activities, as discussed in Software Boxes 5.4 and 5.5 and the Maple worksheets
referenced there (exercise left for the reader). Calculation of a full phase boundary, e.g.
as in Fig. 8.5, is accomplished by including either Peq or Teq in a do loop that iterates
over a pressure or temperature range of interest, e.g. as in worksheet sp_grt_MAS.mw.
The pressure integral of non-condensed phases is handled differently, and will be
discussed in Chapter 9.
Substituting (8.9)in(8.1) and integrating at constant T along a “hot isothermal
compression” path from zero pressure (≈ 1 bar) to the pressure of interest we get:
P
0
V(P,T)dP =V
0,T
P
0
1 +
K
P
K
0,T
−
1
K
dP. (8.23)

396 Equations of state for solids
Making the substitution u = 1 +K
P/K
0,T
, we arrive quite easily at:
P
0
V(P, T)dP =
V
0,T
K
0,T
K
−1
1 +
K
P
K
0,T
K
−1
K
−1
. (8.24)
There are three parameters in this equation: V
0,T
and K
0,T
are functions of temperature only
and K
is a constant (by construction of the Murnaghan EOS, see equation (8.5)).
Holland and Powell use a single-parameter equation for thermal expansion, and make
the case that trying to fit more complex equations to the high-temperature volume data
available for many minerals would amount to “overfitting” – i.e. the more complex empirical
equations would not recover any significant information that is not already recovered by
the one-parameter equation that they propose. Their equation for α is:
α =a
0
1 −10T
−1/2
, (8.25)
where a
0
is an empirical parameter characteristic for each mineral. This equation causes α
to approach the limiting value a
0
at very high temperature, which is the behavior suggested
by Fig. 8.2b. Substituting in (8.11) and integrating we get:
V
0,T
V
0
=exp
a
0
(
T −298
)
−20
√
T −
√
298
. (8.26)
For conditions up to those of the terrestrial mantle transition zone the argument of the
exponential function in (8.26) is always a small number, as a
0
is characteristically of order
10
−5
K
−1
, and temperatures are at most of order 2–3 × 10
3
K. We can then use the approxi-
mation e
x
≈1 +x, for x small (expand e
x
as a McLaurin series if you don’t remember where
this comes from), and we get the following expression for the volume at the temperature of
interest and zero pressure:
V
0,T
=V
0
1 +a
0
(
T −298
)
−20
√
T −
√
298
. (8.27)
Bulk modulus at zero pressure and T is given by (8.17). Holland and Powell list values
of K
0
in their data base, and set the product δ
T
α
0
in equation 8.17 constant and equal to
1.5×10
−4
. This appears to provide a reasonable approximation for crustal and upper mantle
conditions. In any case, because their thermodynamic data base is regressed assuming that
this is the (constant) value of the product δ
T
α
0
, calculations using Holland and Powell’s
data must be carried out with this constant value in equation (8.17) in order to be consistent.
Finally, Holland and Powell point out that the amount of data available for most minerals
only warrants the use of a single value of K
for all minerals, and choose K
=4 as the value
that yields the best fit to all available data. As we shall see below this is also the value of K
that can be expected on theoretical grounds if one assumes that this parameter is constant.
Software Box 8.1 shows that numerical implementation of the pressure integral (8.24)is
very straightforward.
Figure 8.5 (top) shows the spinel–garnet phase boundary (again!), as defined by equilib-
rium among spinel, aluminous enstatite, forsterite and pyrope (see Worked Example 5.6),
calculated both under the assumption that volumes are constant (dashed curve, which is
the same curve as in Fig. 5.9) and using equation (8.24) to account for compressibility and

397 8.2 Macroscopic equations of state
800 1000 1200 1400 160
0
15
20
25
30
etiretsrof
+
eporyp
lenips
+
2
suonimula
etitatsne
Garnet lherzolite
Spinel lherzolite
ROM tabaida
Man elt
so dil us
800 1000 1200 1400 1600
0
0.1
0.2
T(
o
C)
X
lA
X
Al
in enstatite
500 600 700 800
10
20
30
40
Temperature (°C)
Temperature (°C)
Pressure (kbar)
Pressure (kbar)
hp oletipog
+
3
htrona eti
+
2
ztrauq
etivocsum
+
3 edispoid
+
2
etinayk
etiseoc
ztrauq
dnomaid
etihparg
etibla
etiedaj +
ztrauq
Fig. 8.5 Effect of ignoring compressibility and thermal expansion on the calculated locations of the spinel–garnet phase
transition (top) and of some diagnostic ultrahigh-pressure metamorphic reactions (bottom). Note that the error is
not systematic. Thermodynamic data from Holland and Powell, 1998. High-pressure volumes calculated with
Murnaghan EOS.
