Douce A.P. Thermodynamics of the Earth and Planets
Подождите немного. Документ загружается.


398 Equations of state for solids
thermal expansion (solid curve). You may rightly wonder whether the preceding several
pages of formulas and thermodynamic derivations are worth the effort. The difference
between the two calculated phase boundaries is of the order of 100 bars at most, and all
but vanishes at characteristic mantle temperatures (∼1400
◦
C). The difference in calculated
orthopyroxene compositions may barely be outside analytical error. The problem is that this
result is not general. It is a lucky coincidence, arising from the fact that compressibilities
and thermal expansions on both sides of the reaction essentially cancel each other out. This
is not the case if either a particularly “weak” (= small bulk modulus) or “strong” mineral
occurs on one side of the phase boundary, or if thermal expansions vary significantly among
the participating minerals. It is an even greater problem in mineral reactions that evolve a
fluid phase, and in partial melting reactions, as we shall see in the following chapters. The
error incurred by ignoring volume changes of solid phases increases with pressure and is
always unacceptable at pressures higher than a few tens of kilobars.
Figure 8.5 (bottom) shows calculated phase boundaries for some model mineral reac-
tions relevant to the study of utrahigh-pressure metamorphism (UHPM) of crustal rocks
subducted to mantle depths (typically at continental collision zones). In every case the
solid line is calculated accounting for the compressibility and thermal expansion of miner-
als, and is consistent with experimental brackets, whereas calculation of the dashed lines
assumes constant volume. Coesite and diamond are perhaps the two chief diagnostic min-
erals of UHPM. Ignoring volume changes in the reactions graphite diamond and quartz
coesite introduces errors of the order of 3–4 kbar, or about 10% of the actual equilibrium
pressure, and equivalent to a depth uncertainty of ∼10–12 km. These large discrepancies
arise from significant differences in both bulk moduli (diamond =5800 kbar vs. graphite =
390 kbar, coesite = 1000 kbar vs. quartz = 750 kbar) and coefficients of thermal expansion
(a
0
values are: diamond = 1.65 ×10
−5
K
−1
vs. graphite = 4.84 ×10
−5
K
−1
and coesite =
1.8 ×10
−5
K
−1
vs. quartz = 0.65 ×10
−5
K
−1
). Note that the high pressure phase in both
cases is the less compressible one, as one would expect from a closer packed crystalline
structure. Thermal expansion, in contrast, is greater for graphite relative to diamond, but
smaller for coesite relative to quartz.
The two other reactions shown in the figure are the breakdown of albite to jadeite plus
quartz, which we discussed in Worked Example 7.2, and a water-conserving reaction that
models the formation of the assemblage phengite + clinopyroxene in rocks of tonalitic
composition. Reactions such as the latter one, including ones in which amphiboles take
part, may be responsible for inhibiting dehydration-melting (see Worked Example 6.3)of
metamorphosed crust during continental subduction (Patino Douce, 2005). In both of these
cases the effect of ignoring volume changes in solid phases is less severe, but note that the
magnitude of the error is not systematic.
8.2.5 The Birch–Murnaghan isothermal EOS
Derivation of the Birch–Murnaghan EOS begins from a description of finite strain (see,
for example, Birch, 1952). Strain can be measured relative to either the deformed or
undeformed states, leading to different equations. We will describe strain relative to the
deformed state, which is known as the Eulerian convention. Measurement of strain rel-
ative to the undeformed state, known as the Lagrangian convention, leads to a more
cumbersome EOS.
399 8.2 Macroscopic equations of state
Let the distance between two points in a strained material be S, given by S
2
=
X
2
i
,
where X
i
(i =1, 2, 3) is the distance along each of three orthogonal directions. The distance
between the same points in the unstrained state is S
0
, where S
2
0
=
(X
i
−dX
i
)
2
. The
increments dX
i
are the elongations along the three orthogonal directions. We are interested
in changes in volume only, which is a condition that is called isotropic strain. We can thus
make dX
i
= kX
i
, with the same proportionality constant, k < 0 (we are interested in
compression), for all three directions. The change in distance between the points is then
given by:
S
2
−S
2
0
=
X
2
i
−
(
X
i
−dX
i
)
2
=
2k −k
2
X
2
i
=2ε
X
2
i
. (8.28)
The coefficient ε, known as the Eulerian strain, is a second-order tensor with nine com-
ponents ε
ij
, i = 1,2,3, j = 1,2,3. If strain is isotropic then all shear components vanish
(ε
ij
=0 for i =j ) and all principal components are equal (ε
11
=ε
22
=ε
33
). In this special
case the Eulerian strain tensor collapses to the scalar ε (a zeroth-order tensor), which can
be shown to be ε =
1
2
(2k −k
2
), as in (8.28) (Exercise 8.3).
If we now call the strained volume V =
X
i
and let the unstrained volume be the
reference volume V
0
=
(X
i
−dX
i
), we find that (proof left for the reader):
V
0
V
=
(
1 −k
)
3
. (8.29)
We define the parameter f =−ε and with some manipulations find:
f =−ε =−
1
2
2k −k
2
=
1
2
V
0
V
2/3
−1
. (8.30)
Note that for compression it is always f>0. The idea of the Birch–Murhanghan equation
of state is to express the elastic free energy of the material as a power series in the positive
quantity f , and then obtain the isothermal pressure, P
0
, as a derivative of the elastic free
energy. Because we seek to define pressure as a derivative of free energy relative to volume
at constant temperature the relevant thermodynamic potential is the Helmholtz free energy,
F =F(V,T), rather than the Gibbs free energy (see Section 4.8.6, equations 4.124 – 4.126).
We write:
F
e
=a
1
f +a
2
f
2
+a
3
f
3
+··· (8.31)
where the subscript e specifies that this is only the elastic contribution to Helmholtz free
energy. The power series is commonly truncated at the cubic term, which generates what
is known as the third-order Birch–Murnaghan EOS, although the fourth-order term is
sometimes included too (and the algebra, which is already ungainly at third order, becomes
even more so). From equation (4.126) for a constant composition system we have, using
the chain rule:
P
0
=−
∂F
e
∂V
T
=−
∂F
e
∂f
∂f
∂V
. (8.32)
Because:
∂F
e
∂f
=a
1
+2a
2
f +3a
3
f
2
(8.33)

400 Equations of state for solids
and P
0
must vanish in the uncompressed state (f =0), we see that it must be a
1
=0. From
(8.30) we find the other partial derivative in (8.32)tobe:
∂f
∂V
=−
1
3V
0
(
2f +1
)
5/2
(8.34)
so:
P
0
=
f
3V
0
(
2a
2
+3a
3
f
)(
2f +1
)
5/2
. (8.35)
There are two unknown parameters in this equation, a
2
and a
3
, which can be evaluated if we
find two linearly independent equations that relate these two parameters to experimentally
observable quantities. For example, we can fix the values of two of the derivatives of P
0
at some reference pressure, such as zero pressure (because (8.35) vanishes at zero pressure
we cannot use this equation). Applying the chain rule to the definition of isothermal bulk
modulus we get:
K
T
=−V
∂P
0
∂V
T
=−V
∂P
0
∂f
∂f
∂V
. (8.36)
We already have ∂f/∂V (equation (8.34)). Calculation of ∂P
0
/∂f involves some rather unin-
teresting algebra. You can do it yourself, or have Maple do it for you, and verify the
result:
K
T
=
(
2f +1
)
5/2
9V
0
2a
2
+
(
14a
2
+6a
3
)
f +27a
3
f
2
. (8.37)
Evaluating (8.37)atf =0 (i.e. zero pressure) we find:
K
0,T
=
2a
2
9V
0,T
. (8.38)
We can also take the pressure derivative of K
T
,K
T
:
K
T
=
∂K
T
∂P
=
∂K
T
∂f
∂f
∂P
(8.39)
and, after some additional uninteresting algebra and evaluation at zero pressure, arrive at:
K
0,T
=
a
3
a
2
+4. (8.40)
From (8.38) and (8.40) we can get the values of a
2
and a
3
in terms of three parameters
that are experimentally accessible: V
0,T
, K
0,T
, and K
0,T
. Substituting these values and
the definition of f (equation 8.30) in the pressure equation (8.35) we finally arrive at the
(Eulerian) Birch–Murnaghan equation of state to third order:
P
0
=
3
2
K
0,T
V
0,T
V
7/3
−
V
0,T
V
5/3
1 +
3
4
V
0,T
V
2/3
−1
K
0,T
−4
.
(8.41)
The subscript T in the three parameters, V, K and K
in (8.41) makes it clear that this is an
isothermal equation of state that can be used at any temperature, provided that the values of

401 8.2 Macroscopic equations of state
the three parameters are known at that temperature. If the equation is applied to calculation
of isothermal compression at the reference temperature (cold isothermal compression in
Fig. 8.1) then the parameters are labeled V
0
, K
0
and K
0
, but it is always necessary to
specify whether the reference temperature is 298 K or 0 K.
The second-order Birch–Murnaghan EOS is obtained by setting a
3
= 0 (see
equation (8.31)). This makes K
0
constant and equal to 4 (equation (8.40)) which is the
value used in the Holland and Powell data set, and is comparable to the value measured for
many minerals. The resulting second-order EOS is:
P
0
=
3
2
K
0,T
V
0,T
V
7/3
−
V
0,T
V
5/3
. (8.42)
Note that, in contrast to the Murnaghan EOS, both forms of the Birch–Murnaghan EOS are
pressure-explicit and have no analytic solutions for V.
Worked Example 8.2 The ringwoodite–perovskite phase transition in planetary mantles
If, as a first approximation, we neglect the relatively minor components Al and Ca, then the
chemical composition of the mantles of the terrestrial planets approaches (Mg,Fe)
2
SiO
4
,
with X
Mg
∼0.9 for the Earth’s mantle and ∼0.8 for the mantles of Mars and the Moon
(Mg number for the mantles of Venus, Mercury and other rocky bodies are far less well
constrained). At near-surface conditions these components occur as the mineral olivine –
in fact, the stability field of olivine is what defines the Earth’s upper mantle. Olivine
undergoes phase transformations with increasing pressure, which are observed as discon-
tinuities in seismic velocities. In the Earth the first such discontinuity occurs at a depth of
∼410 km, where olivine transforms to the isochemical phase wadsleyite which has a
spinel-like structure. At a depth of ∼520 km wadsleyite in turn transforms to ringwoodite,
also (Mg,Fe)
2
SiO
4
but with a true spinel structure. Density increases from olivine to
wadsleyite to ringwodite, but in all three phases silicon occurs in tetrahedral coordination.
At a depth of approximately 660 km in the Earth’s mantle a major phase transformation
takes place, in which ringwoodite breaks down to a phase with perovskite structure
and composition (Mg,Fe)SiO
3
, and an oxide phase of composition (Mg,Fe)O, which is
called either magnesiowüstite or, more appropriately in view of its relative Mg and Fe
contents, ferropericlase. This transformation, in which a silicate perovskite phase with Si
in octahedral coordination becomes stable, marks the top of the Earth’s lower mantle. The
depth interval 410–660 km, over which the olivine–wadsleyite–ringwoodite–perovksite
phase transitions take place, is known as the mantle transition zone. Other reactions
involving Al- and Ca-bearing phases such as pyroxenes, majoritic garnets and calcium
perovskite also take place in the mantle transition zone. Completing the picture, there is a
“final” silicate phase transition that occurs close to the Earth’s core–mantle boundary and
corresponds to the D
seismic discontinuity. It has recently been found experimentally that
this phase transition gives rise to a dense silicate phase that is isochemical with perovskite,
and is at the time of this writing called the “post-perovskite phase”.
In this example we will calculate the ringwoodite–perovskite phase boundary, and see
what we can learn from it about deep planetary interiors. There are some significant
complications, not the least of which is the paucity of well-constrained standard state ther-
modynamic properties. It is known from experimental results that ringwoodite–perovskite

402 Equations of state for solids
phase relations are shifted significantly in P and T between the Mg and Fe end-member
systems. In fact, at P–T conditions such as those of the terrestrial mantle transition zone
Fe-perovskite is not stable, and Fe-ringwoodite breaks down to the assemblage wüstite +
stishovite. We will thus consider the four phases: perovksite (pv = MSiO
3
), ringwoodite
(rw = M
2
SiO
4
), ferro-periclase (pc = MO) and stishovite (st = SiO
2
), where M stands for
Mg or Fe, and calculate the following four univariant reactions in each of the two-component
end-member systems.
rw pv +pc (st)
pv pc +st (rw)
rw 2pc +st (pv)
2pv rw +st (pc)
We need a full set of standard state thermodynamic properties, and here is the first prob-
lem. As of this writing there appears to be no updated and internally consistent data base for
high pressure phases comparable to, for example, those of Holland and Powell or Berman
for crustal and upper mantle phases. Part of the problem is that these ultra-high-pressure
phases are difficult to synthesize in enough quantity to allow accurate calorimetric mea-
surements, and the error bars in pressure and temperature of phase equilibrium experiments,
that can also be used to derive values of thermodynamic functions, can be considerable. I
have chosen to harvest thermodynamic data from three sources: Matsuzaka et al. (2000),
Frost et al. (2001) and Mattern et al. (2005), as a reasonable compromise between quality
and “recentness” of data, on the one hand, and mutual consistency in the treatment of heat
capacities, thermal expansion coefficients and bulk moduli on the other. As we shall see, the
results of the calculations are generally supportive of this choice. Both C
P
and α for these
high-pressure phases are expressed by different polynomials from those used by HP98, so
that new Maple procedures are needed in order to implement the heat capacity and volume
integrals (this is of course trivial, see Software Box 8.2). The corresponding equations are:
C
P
=a
1
+a
2
T +a
3
T
−2
+a
4
T
2
+a
5
T
−3
+a
6
T
−1/2
+a
7
T
−1
(8.43)
and:
α =α
0
+α
1
T +α
2
T
−2
. (8.44)
There appears to be some consensus that, at pressures such as those of the mantle transition
zone and higher (we will calculate what those pressures are later), the third-order Birch–
Murnaghan EOS reproduces mineral volumes reasonably well. In contrast to the Murnaghan
EOS, however, the Birch–Murnaghan EOS cannot be written in volume-explicit form, so
that VdP must be integrated by parts:
P
0
VdP = PV
P ,T
−
V
P ,T
V
0,T
PdV, (8.45)
where V
0,T
is the zero pressure volume and V
P ,T
is the volume at the pressure of interest,
both of them taken at the temperature of interest. If one wishes to calculate thermodynamic
functions at a given pressure, for example to locate a phase boundary, it is necessary first to
solve (numerically) for V
P ,T
, and then integrate (8.45), substituting the desired pressure-
explicit EOS. Both of these steps are handled with ease by Maple (Software Box 8.2).

403 8.2 Macroscopic equations of state
1000 1500 2000
150
200
250
300
Temperature (°C)
Pressure (kbar)
Mg-rw
Mg-pv
+ Mg-pc
Mg-rw +
st
Mg-pv
Mg-rw
Mg-pc
+
st
Mg-pc
+st
Mg-pv
Fe-rw
Fe-pc
+
st
Fe-pc +
st
Fe-pv
Fe-rw
Fe-pv
+
Fe-pc
Fe-rw
+ st
Fe-pv
[Fe]
[Mg]
(rw)
(pv)
(pc)
(st)
pc pv st
pc rw pv st
pc rw st
pc st
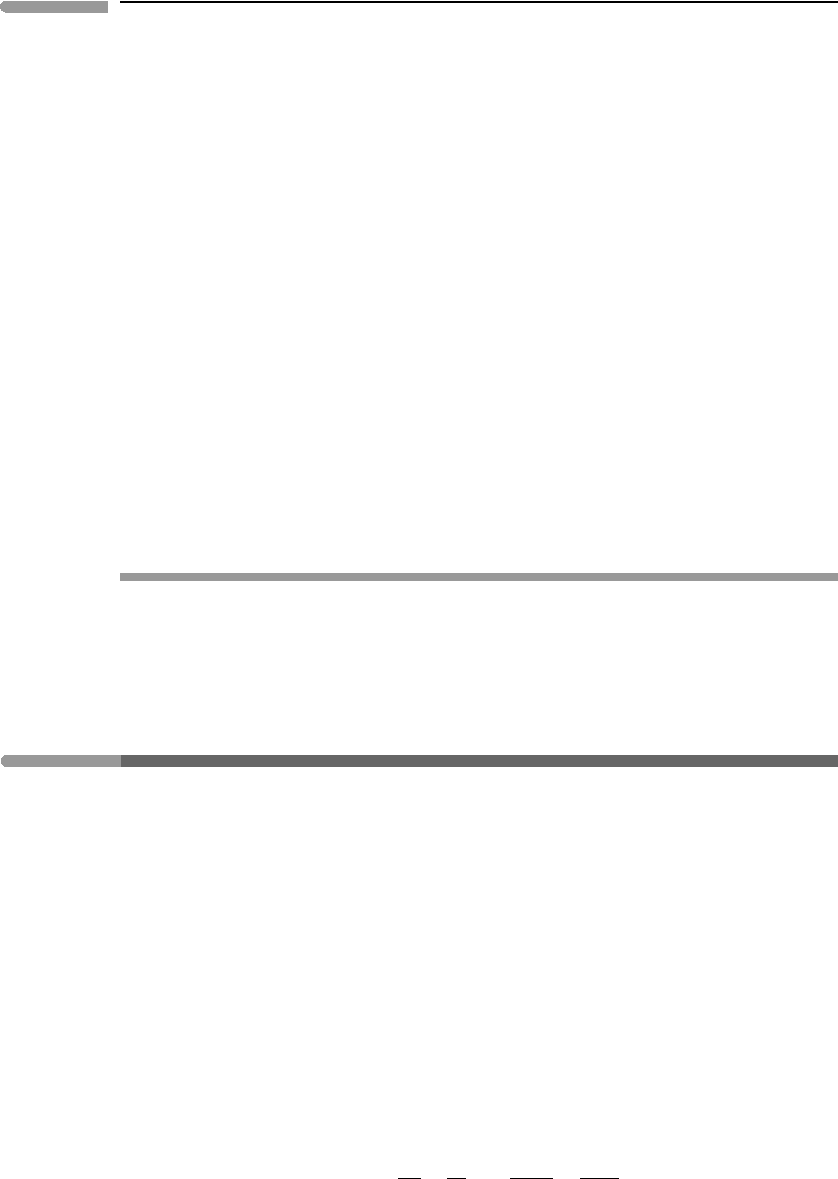
Fig. 8.6 Calculated reactions among ringwoodite (rw), silicate perovskite (pv), ferropericlase (pc) and stishovite (st), for the
Mg and Fe end-member systems. The dashed line shows a possible path of the pseudo-invariant point for ternary
systems of intermediate composition (it is not a phase boundary!), but note that the actual path does not have to
be a straight line. Inset shows schematic phase relations, to emphasize Schreinemakers’ legality. Thermodynamic
data from Matsuzaka et al. (2000), Frost et al. (2001) and Mattern et al. (2005). High-pressure volumes calculated
with third-order Birch–Murnaghan EOS.
Software Box 8.2 Maple worksheets for thermodynamic calculations with solid phases at
very high pressures.
Holland and Powell estimate that their data base is reliable to pressures of order 100
kbar. Different data, and different equations, must be used to handle thermodynamic
calculations at higher pressures. I include many commonly used calculations in two
packages, so that they can be called from any other Maple worksheet.
The package th_hiP.mw parallels th_shomate.mw but substitutes heat capac-
ity equation (8.43) for the Holland and Powell (Shomate-style) equation used in
th_shomate.mw. Package th_hiP.mw contains procedures that calculate Cp,
Cp,
Cp/T, H , S and G. There is also a procedure that calculates zero-pressure volume, V(T),
by integration of equation 8.11 using equation (8.44) to express α(T ), and a procedure
that calculates zero pressure bulk modulus K(T ) using equation (8.46). Except for bulk

404 Equations of state for solids
modulus, parameters are passed in a one-dimensional array in which elements 1 through
7 are heat capacity coefficients (equation (8.43)), element 8 is standard state enthalpy,
element 9 is standard state entropy, element 10 is standard state Gibbs free energy
(can be set to zero if desired), element 11 is volume and elements 12 through 14 are the
coefficients of the thermal expansion equation (8.44). Bulk modulus at zero temperature
and dK/dT (equation (8.46)) are passed as individual variables.
The package S_EOS.mw contains procedures that calculate pressure and the value of
VdP (integrated by parts, see equation (8.45)) for the pressure-explicit version of the
Murnaghan EOS (solve equation (8.9) for P ), the third-order Birch–Murnaghan EOS
(equation (8.41)), the second-order Birch–Murnaghan EOS (equation (8.42)), and the
Born–Mie EOS (equation (8.56)). The rather messy
PdV definite integrals are handled
implicitly by Maple, resulting in very compact procedures.
Worksheet delgcalc_hi_p.mw contains examples of the use of some of the
procedures in these packages, applied to the calculation of phase boundaries among
pure end-member high pressure phases. This worksheet was used to construct Fig.
8.6. Procedures load and deltareax work as in previous examples (see Software
Box 1.1), but load is slightly modified to accommodate the different format of the high
pressure data set. Procedure vdp calculates
VdP for each phase in the reaction, and
adds up the total pressure contribution to the Gibbs free energy of reaction. Procedure
dGPT calculates the total Gibbs free energy of reaction at P and T. Solution of the
equilibrium condition is implemented in delg0 which uses an iterative procedure, as
the integral in the vdp procedure does not allow use of Maple’s fsolve facility. delg0
solves for pressure (in kbar) at given T (in centigrade) and requires an initial pressure
guess. A value of 500 kbar appears to be a good choice for the initial pressure guess.
Procedure delg0 finds equilibrium conditions among pure end-member phases, but
can be easily modified if desired to find equilibrium among solid solutions, by adding
an RTln K term.
Calculation of a phase boundary among pure end-member phases is accomplished
by the do loop in Pbound, which works in the same way as in many similar prior
procedures. Input parameters are the reaction name, the range of temperatures over
which to solve, the temperature increment between consecutive solutions, the initial
pressure guess, and the name of the output file.
The statement block at the end of the worksheet defines the stoichiometries of all of
the reactions included in the phase diagram in Fig. 8.6. Remember that this statement
block must be executed before the phase boundary calculation is attempted, or an error
message will result.
The third-order Birch–Murnaghan EOS contains three parameters. V
0,T
is calculated
from (8.11), using (8.44). In the data sources used for this example K is assumed to be a
linear function of temperature, so that:
K
0,T
=K
0
+
dK
dT
(
T −T
0
)
. (8.46)
Finally, K
is also treated as a constant, but with different and characteristic values for
each phase (compare Holland and Powell’s treatment for lower pressure phases, in which all
phases are assigned the same value of K
). Values of K
0
,K
and ∂K/∂T, as well as of all
405 8.3 Isothermal equations of state
the other thermodynamic parameters, for all of the phases used in this exercise are given
in Matsuzaka et al. (2000), Frost et al. (2001) and Mattern et al. (2005). The numerical
implementation is discussed in Software Box 8.2, and the results are shown in Fig. 8.6.
The calculated reactions are consistent with Schreinemakers’s rule, as shown in the inset
diagram. The invariant points for each of the two end-member systems are labeled [Fe]
and [Mg]. The Fe-absent system, [Fe], is more closely applicable to the mantles of the
terrestrial planets. As we shall see later, the temperature in the Earth’s mantle at the 660 km
discontinuity may be ∼1600
◦
C, which in the Mg end-member system corresponds to a
pressure of ∼245 kbar. As we shall also see, this corresponds to a depth of ∼700 km, which
is close to, but not exactly, the expected value. The calculated phase diagram shows that
adding Fe to the system shifts the equilibrium to lower pressures, with the invariant point
following a path such as the one suggested by the dashed line (the actual path does not
have to be a straight line – the line is for illustrative purposes only). In another numerical
example towards the end of this chapter we will incorporate the effect of varying X
Mg
and
see whether a better agreement with the depth of the observed seismic discontinuity can be
obtained.
An interesting feature of the phase diagram in Fig. 8.6 is that the ringwoodite–perovskite
phase transition has a negative Clapeyron slope (as this is true of both end-member systems
it is almost certainly true in general). This means that if the transition is crossed isothermally,
or nearly so, in the direction of increasing pressure (V < 0) then the reaction is endothermic
(H = TS>0) and, conversely, it is exothermic during decompression.
8.3 Isothermal equations of state from interatomic potentials:
the Born–Mie EOS
Consider equation (8.2) (with P
el
= 0) and let us define the pressure components more
rigorously. We shall require that all of the energy of vibration of atoms about their equi-
librium positions be expressed macroscopically as thermal pressure, P
th
. We will derive
expressions for P
th
in Section 8.4. For now we focus on the fact that from this requirement it
follows that P
th
vanishes at 0 K. The pressure associated with isothermal compression at 0
K arises only from the energy of position of the atoms or, more accurately, from changes in
the energy of position that arise from changes in interatomic distances (i.e. P =−∂E/∂V if
T =0, see equation (4.12)). Now, in order for a crystalline structure to be stable (i.e. neither
collapse nor fly apart) there must be both attractive and repulsive forces between atoms.
The equilibrium interatomic distance is where the two forces balance each other out. We
can then express the energy of position of the atoms, also called the lattice energy, E
L
,as
the sum of an attractive (negative) potential and a repulsive potential (recall the definition
of potential from Section 1.3.1):
E
L
=−
a
r
m
+
b
r
n
=−
a
V
m/3
+
b
V
n/3
, (8.47)
406 Equations of state for solids
where a, b, m and n are positive constants, r is the equilibrium interatomic distance, and V
is the equilibrium volume (which goes as the cube of r). At absolute zero we can write:
P
0
=−
∂E
L
∂V
. (8.48)
Note very carefully that, because the natural variables of internal energy are volume and
entropy, the isothermal derivative (8.48) is true only at 0 K (see equation (4.12)). Isothermal
EOS derived from interatomic potentials are therefore only strictly correct at zero tempera-
ture, and in this case we must take V
0
at T
0
=0 K, even if the difference in volume between
0 K and 298 K is small and is often ignored.
Applying (8.48)to(8.47) we get:
P
0
=−
am
3
V
−
m+3
3
+
bn
3
V
−
n+3
3
. (8.49)
We now seek the values of two of the constants, a and b, in terms of m and n. Why will
become clear soon – for now we note that we need two linearly independent equations in a
and b. From (8.49) at zero pressure we easily find:
a
b
=
n
m
V
(
m−n
3
)
0
. (8.50)
We can also calculate the bulk modulus from (8.49):
K
T
=−V
∂P
∂V
T
=−
am
(
m +3
)
9
V
−
m+3
3
+
bn
(
n +3
)
9
V
−
n+3
3
. (8.51)
Evaluating 8.51 at zero pressure (V =V
0
) and using (8.50) we find:
a =
9K
0
m
(
n −m
)
V
m+3
3
0
, b =
9K
0
n
(
n −m
)
V
n+3
3
0
, (8.52)
where K
0
is the isothermal bulk modulus at 0 K and zero pressure. Substituting in (8.49)
we finally arrive at:
P
0
=
3K
0
m −n
V
0
V
m+3
3
−
V
0
V
n+3
3
. (8.53)
This equation is known as the Mie equation of state. It is not complete, as the values of the
exponents m and n in (8.47) are still undetermined (see also Exercise 8.4). The simplest
way of addressing this is to assume that the attractive potential is due only to electrostatic
forces, which vary as the inverse square of distance, so that m =1 (compare equation (1.8)
for the gravitational potential). We then need an additional equation to get the value of n,
which can be estimated from the pressure derivative of K at zero pressure, K
0
. Applying
the definition of bulk modulus to (8.53) we find:
K =
K
0
m −n
(
m +3
)
V
0
V
m+3
3
−
(
n +3
)
V
0
V
n+3
3
. (8.54)

407 8.4 Thermal pressure
Note that in (8.54) K
0
is the bulk modulus at zero pressure and zero temperature, whereas
K is the bulk modulus at some other pressure (given by the value of V), but still at zero
temperature. Differentiating (8.54) relative to P (more uninteresting algebra) and evaluating
at zero pressure we get the pressure derivative of the bulk modulus at zero pressure and
zero temperature:
K
0
=
1
3
(
n +m +6
)
. (8.55)
Substituting m = 1 and n from (8.55)in(8.53) we arrive at the following equation, known
as the Born–Mie EOS:
P
0
=
3K
0
3K
0
−8
V
0
V
3K
0
−4
3
−
V
0
V
4
3
. (8.56)
8.4 Thermal pressure
We can argue on the basis of physical intuition that thermal pressure must vary directly
with the vibrational energy of atoms about their equilibrium positions, and inversely with
volume, i.e.:
P
th
=γ
E
vib
V
. (8.57)
This equation states that thermal pressure is proportional to the vibrational energy density.
The proportionality factor γ is known as the Grüneisen ratio and appears in a number
of geophysical applications. Equation (8.57) is the starting point for statistical mechani-
cal approaches to calculating thermal pressure. These entail finding expressions for E
vib
as sums of individual vibrational modes and allow, in principle, ab initio calculations of
thermal pressure, i.e. calculations that rely on minimal empirical knowledge of specific
material properties. Such calculations are beyond the scope of this book, and I mention them
only for completeness. We will calculate thermal pressure following a thermodynamic (i.e.
macroscopic) approach.
From (8.2), and neglecting electron pressure, we have:
∂P
∂T
V
=
∂P
0
∂T
V
+
∂P
th
∂T
V
. (8.58)
Because in (8.2) we defined P
0
at constant temperature, the first term in the right-hand side
of (8.58) vanishes. Using identity (8.18) we infer:
∂P
th
∂T
V
=αK
T
. (8.59)
Thermal pressure can therefore be calculated by integrating the product of the (macroscopic)
material properties αK
T
. We shall return to this integral in a moment. First, we note that
