Douce A.P. Thermodynamics of the Earth and Planets

Подождите немного. Документ загружается.

418 Equations of state for solids

225

0.6

0.7 0.8

0.9

230

235

240

245

X (Mg)

Pressure (kbar)

ringwoodite

perovskite + periclase

pv+pc

T = 1600°C

~7km

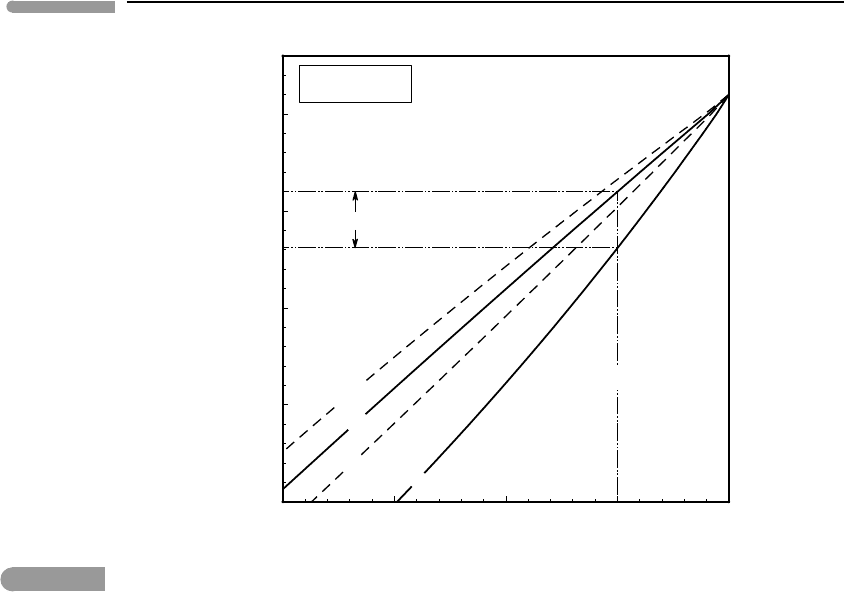
Fig. 8.12 P–X

loop (compare Fig. 6.18) for the ringwoodite to silicate perovskite +ferropericlase phase transition at

1600

◦

C.Silicateperovskitebecomesmetastablerelativetoferropericlase+stishoviteforP–Xcombinationscloseto

thelowerboundsofthediagram(seeIto&Takahashi,1989;Matsuzakaetal.,2000;Frostetal.,2001).Forbulk

=0.9, and assuming that temperature is constant (which is approximately correct for a convective mantle), the

divariant phase transition is “spread out” between 238 and 241 kbar, corresponding to a depth interval of ∼7 km.

different X

on one side of the reaction. In Fig. 8.12 I show the composition of ringwood-

ite with a solid curve, and the compositions of the two phases that coexist on the other

side of the reaction, perovskite and periclase, with broken lines. The bulk composition of

the assemblage perovskite + periclase must lie between these two curves, and is shown

schematically with a solid curve. The two solid curves, labeled rw and pv + pc, are the

boundaries of the divariant phase transition at the 670 km discontinuity. For a mantle with

=0.9, breakdown of ringwoodite at 1600

◦

C begins at ∼238 kbar and is completed at

∼241 kbar. Thus, the divariant assemblage ringwoodite + perovskite + periclase coexists

at equilibrium over a pressure interval of ∼3 kbar, which corresponds to a depth interval of

∼7 km (see, Fig. 8.8). This result compares favorably with estimates based on the sharpness

of the seismic discontinuity.

Let us now repeat the exercise for the Martian mantle. In this case we use the zero-

temperature Born–Mie pressures shown in Fig. 8.10 and temperatures calculated with (8.70)

assuming T

=2000 K at z

=700 km (see Section 3.9). Using zero-temperature pressures

is justified by our finding that thermal pressure in the Martian mantle is likely to be small.

The resulting P –T curve is labeled Martian adiabat in Fig. 8.11, and terminates at the

pressure of the Martian core–mantle boundary (CMB), shown with a star in the figure.

Calculated conditions at the Martian CMB are ∼200 kbar and ∼2180 K, for which the

solution set of equations (8.73)isX

=0.6, X

=0.64 and X

=0.53. Given that the

Martian mantle is more magnesian than this (Mg number about 80), and that the perovskite

419 8.4 Exercises for Chapter 8

phase transition at any pressure less than that of the CMB would require an even more

Fe-rich composition than that calculated for the CMB (see Fig. 8.11), we can infer that

perovskite does not exist in the Martian mantle. Moreover, if the temperatures estimated

in Section 3.9 are approximately correct, then the Martian adiabat also stays on the high

temperature side of the invariant point, and breakdown of ringwoodite to ferropericlase +

stishovite is also inhibited. We can thus conclude that the silicate phase at the base of the

Martian mantle is likely to be ringwoodite.

Exercises for Chapter 8

8.1 The ringwoodite–perovskite transition, that defines the bottom of the mantle transition

zone, has a negative Clapeyron slope (Fig. 8.6). In contrast, the olivine–wadsleyite

transition, that defines the top of the transition zone, has a positive Clapeyron slope.

Discuss how each of these transitions may affect the mantle adiabat.

8.2 Prove identity 8.20:



∂α

∂P





∂K

∂T



. (8.20)

8.3 Prove that if all shear strain components vanish (ε

= 0 for i = j ) and all diagonal

elements of the strain tensor are equal (ε

=ε

) then strain is isotropic, meaning

that elongation is proportional to the distance between points only, and independent of

orientation. Also, prove that in this special case Eulerian strain is related to the pro-

portionality constant between elongation and distances by ε =

(2k −k

), see Section

8.2.5.

8.4 Note that the Mie EOS (equation (8.53)) is formally identical to the second-order

Birch–Murnaghan EOS (equation (8.42)). To make it identical would require that m =

4 >n= 2. Is this physically reasonable? Explain why. (Hint: find the extrema of the

function.) How does the Born–Mie EOS get around this problem?

8.5 Reproduce Figs. 8.8 and 8.9, using the Maple worksheets described in Software Box 8.3.

Plot density vs. pressure in the simplified three-layer mantle described in these figures.

Comment on your results.

8.6 On the basis of the discussion in Section 3.9, construct a possible adiabat for Venus.

Assuming that the Venusian mantle has the same composition as the terrestrial mantle,

estimate the depth of the ringwoodite–perovskite transition in Venus. As a very rough

approximation estimate the depth of the olivine-ringwoodite (metastable) transition by

scaling your result to Fig. 8.9. Calculate curves of zero-temperature pressure vs. depth

and thermal pressure vs. depth for Venus, and comment on your results.

8.7 The phase diagram in Fig. 8.12 shows that the high-pressure assemblage perovskite +

ferropericlase is richer in Fe than the low-pressure phase ringwoodite. Yet the mantle

transition zone is an isochemical boundary. Explain the apparent contradiction.

Thermodynamics of planetary volatiles

From a physical point of view a fluid is a material that lacks shear strength, i.e. that deforms,

or “flows”, when subject to shear stress. The strain rate for a given shear stress is of course

highly variable, and defines the viscosity of the fluid. From a chemical thermodynamic point

of view it is convenient to distinguish between different types of fluids. There are fluids with

relatively low densities and low viscosities, which tend to be highly mobile in planetary

environments. These are often referred to as “volatiles”, and are typically composed of

species in the system C–O–H–N–S–F–Cl, with inert gases (particularly He) also important

in gas giants. There are also fluids with generally higher densities than volatiles, which

also have much higher viscosities, typically by several orders of magnitude. If such fluids

exist at equilibrium with solids of broadly similar bulk composition we call them melts

(Chapter 10). Melts in terrestrial planets are chiefly silicates, although natural carbonate

melts also exist, as do metallic melts in planetary cores. Melts in icy satellites, in contrast,

are likely to be composed chiefly of species in the system C–O–H–N. A third type of

fluids are liquids at conditions that are far removed from equilibrium with solids of similar

bulk composition, but that may contain species in solution that crystallize their own solids.

Aqueous solutions (Chapter 11) are an example.

The boundaries between these different types of fluids are not always clearly defined.

In this chapter we will discuss the thermodynamics of fluids that can be described as

volatiles. These can be gases, i.e. non-condensed phases that expand indefinitely, liq-

uids, which are condensed and strongly incompressible fluids, or supercritical fluids,

whose physical properties vary continuously between those of gases and liquids (see also

Section 1.15).

9.1 Fugacity and standard state fugacity

In Chapter 5 we saw that the chemical potential of a gas species, i, in a mixture of ideal

gases at total pressure P is given by:

P ,T

=µ

0,i

(o)

+RT ln



(o)



=µ

0,i

(o)

+RT ln



(o)



, (9.1)

where p

is the partial pressure of species i in the mixture, and P

(o)

is the pressure of some

arbitrarily chosen standard state, in which species i is pure. In Chapter 5 (e.g. equation (5.86))

we chose P

(o)

=1 bar, and this is indeed the usual practice for gases. We shall return to this

convention soon, but for clarity in the following derivations it is best to leave the value of

(o)

temporarily unspecified.

420

421 9.1 Fugacity and standard state fugacity

We can write the chemical potential of a gas species in a mixture of real gases as a

combination of ideal and excess, or residual, contributions:

P ,T

=µ

P ,T ,id

+µ

P ,T ,res

=µ

0,i

(o)

+RT ln



(o)



+µ

P ,T ,res

. (9.2)

We now define a dimensionless parameter φ

, called the fugacity coefficient of species i in

the mixture, by the expression:

RT ln φ

≡µ

P ,T ,res

(9.3)

and re-write (9.2) as follows:

P ,T

=µ

0,i

(o)

+RT ln



(o)



. (9.4)

We can collect the terms in the numerator of the logarithmic function and define a new

thermodynamic function, called fugacity, by means of the following two equations:

≡X

P (9.5)

lim

P →0

=1. (9.6)

Note the following properties of fugacity: (i) equation (9.5) defines fugacity as a phys-

ical quantity with units of pressure, (ii) equation (9.3) makes the fugacity of an ideal

gas (µ

res

=0) identical to its partial pressure, or its total pressure if X

= 1, and

(iii) equation (9.6) states that at vanishingly small total pressure the fugacity of any gas is

equal to its partial pressure. As long as T !0 (e.g. T ≥298 K), a pressure of 1 bar is under

most circumstances low enough for (9.6) to be valid. Unless otherwise stated, then, we shall

assume that (9.6) is always valid at 1 bar and call this condition the ideal gas limit. We also

note that, although not explicitly stated in (9.3) and (9.5), fugacity and fugacity coefficient

are functions of temperature and pressure.

Let us consider now the special case of a pure gas. In this case X

= 1 and we re-write

(9.5) as follows:

=φ

P , (9.7)

where f

and φ

are called the standard state fugacity and standard state fugacity

coefficient, respectively. Considering (9.4) for a pure substance and substituting (9.7)

we find:

P ,T

=µ

(o)

+RT ln



(o)



. (9.8)

In equation (9.8) I dropped the superscript i to emphasize that we are now dealing with a

pure substance. The two chemical potentials in this equation can be taken as two possible

standard states, at P and P

(o)

. Using the relationship V =(∂G/∂P )

we can also relate the

two standard states as follows:

P ,T

=µ

(o)



(o)

VdP, (9.9)

422 Thermodynamics of planetary volatiles

which results in:

RT ln



(o)





(o)

VdP. (9.10)

We now introduce the usual convention for gases, i.e. P

(o)

=1 bar, and (9.10) becomes:

RT ln f



VdP, (9.11)

which is the definition of standard state fugacity. We will use this equation to calculate f

(Section 9.5). Note that, as I will do from now on, I have omitted the denominator in the

argument of the logarithmic function in (9.11). It must be tacitly understood that we are

dividing by 1 bar, however, so that fugacity retains its pressure dimension.

With the convention P

(o)

=1 bar equation (9.8) becomes:

P ,T

=µ

1,T

+RT ln f

, (9.12)

which shows that standard state fugacity is a function that converts the standard state of a

real gas at 1 bar to the standard state at any arbitrary pressure P, and at the same temperature.

Physically we can think of the standard state fugacity of a real gas as its thermodynamic

effective pressure, i.e the pressure that an ideal gas with the same chemical composition

would have to be under in order to generate the observed chemical potential of the real

gas (compare (9.12) with (9.1), setting X

= 1). Equation (9.12) provides a simple way of

calculating the standard state chemical potential of a pure gas species at any pressure and

temperature. We first take the gas from the reference temperature (298 K) to T, at a constant

pressure of 1 bar, by evaluating the heat capacity integrals for enthalpy and entropy (Box

5.1). This yields µ

1,T

: the standard state chemical potential at 1 bar and T. We then add the

standard state fugacity term, in order to obtain the standard state chemical potential at P and

T. The standard state fugacity is calculated by integrating (9.11), substituting an appropriate

equation of state. The choice of equation of state, and the integration procedure, will be

discussed later in this chapter.

If we now consider a gas species in a mixture of real gases then substituting (9.5)in(9.4)

we get:

P ,T

=µ

0,i

1,T

+RT ln f

(9.13)

where in this case the fugacity of species i in the mixture, f

, plays the role of a thermo-

dynamic effective partial pressure. A more useful interpretation of equation (9.13) is that it

defines fugacity as a measure of the difference between the chemical potential of a species

in its 1 bar standard state and the chemical potential of the species in the system of inter-

est, regardless of whether or not the species is actually present in a fluid phase, or even

of whether or not a fluid phase is present. Note that even though we defined fugacity by

considering the behavior of chemical species in a gas phase, equation (9.13) as interpreted

in the previous sentence is an equally valid definition of fugacity, that makes no a priori

statement regarding the existence of a fluid phase. In fact, we can also start from (9.13) and

work our way backwards to equation (9.1), which is how fugacity was initially defined by

G. N. Lewis, about a century ago.

The importance of interpreting fugacity as a difference between chemical potentials is

that it makes it possible to attach physical meaning to results such as the one that we obtained

423 9.1 Fugacity and standard state fugacity

in Worked Example 5.5. There we calculated a partial pressure of oxygen of order 10

−40

bar. It is hard to make sense of this number from a molecular point of view, but in terms

of fugacity it is easily understood as a representation of the chemical potential of oxygen,

relative to that of pure oxygen at the same temperature and 1 bar. Comparing (9.12) with

(9.13) it also follows that the activity of species i in a fluid, a

is given by:

. (9.14)

Although (9.14) is rigorously correct we shall not use this relationship, as it is redundant.

Because of the condition imposed by equation (9.6) fugacity is defined in absolute terms,

relative to the behavior of the ideal gas at vanishingly small pressure, and it is a number

that by itself carries all the information that we need.

Worked Example 9.1 Mineral-fluid reactions: hydration of peridotites

Mantle peridotites emplaced in the Earth’s continental crust, or incorporated into the ocean

floor, typically undergo retrograde metamorphism. The anhydrous high-temperature ultra-

mafic assemblage is replaced partially or completely by hydrous minerals, transforming the

rock into a serpentinite. A simple Mg end-member model reaction for this process is the

formation of chrysotile from forsterite plus enstatite, according to:

2Mg

SiO

+Mg

+4H

→

←

2Mg

(

)

. (9.15)

In the presence of a volatile phase that contains no species other than H

O this is a univariant

reaction. If we choose the value of one intensive variable, for example, temperature, then all

other intensive variables are fixed by the assemblage. This includes the chemical potential

of H

O or, equivalently, the fugacity of H

O, which in this case must be the standard

state fugacity, f

O), at the equilibrium temperature and pressure. Volatiles in planetary

interiors are seldom composed of pure H

O, however, and may contain C, S, N, F and Cl in

addition to H and O. The variance of an equilibrium such as (9.15) in nature is thus greater

than 1. Regardless of what the actual variance of the system is, however, as long as the

three solid phases in (9.15) coexist at equilibrium the chemical potential of H

O is fixed

by this equilibrium. This means that fixing T and P fixes the fugacity of H

O, f (H

O).

We state this by saying that the assemblage enstatite + forsterite + chrysotile buffers the

fugacity, or chemical potential, of H

O.We note from our preceding discussion that it must

be f (H

O)≤f

O), with the equality holding only for the special case of univariant

equilibrium, in which no other components are present in the fluid phase.

In order to calculate the fugacity of H

O buffered by (9.15) we write the equilibrium

condition for this reaction as follows:



0,(9.15)

1,T



V

solids

dP −4RT ln f

(

)

=0. (9.16)

Note that in (9.16) the standard state Gibbs free energy change is calculated at 1 bar and

the temperature of interest. The contribution of pressure to Gibbs free energy change is

then split into two components that are calculated separately, one for the solid phases

and the other for the gas species. This is necessary because the equations of state for

424 Thermodynamics of planetary volatiles

solids and gases are different, as we will see later in this Chapter. We discussed how to

calculate the standard state Gibbs free energy change in Chapter 5 (e.g. Box 5.1), and how

to calculate the pressure integral for solids in Chapter 8. Hence, calculation of f (H

from (9.16) is easily implemented in Maple by calling on previously written procedures

(Exercise 9.1).

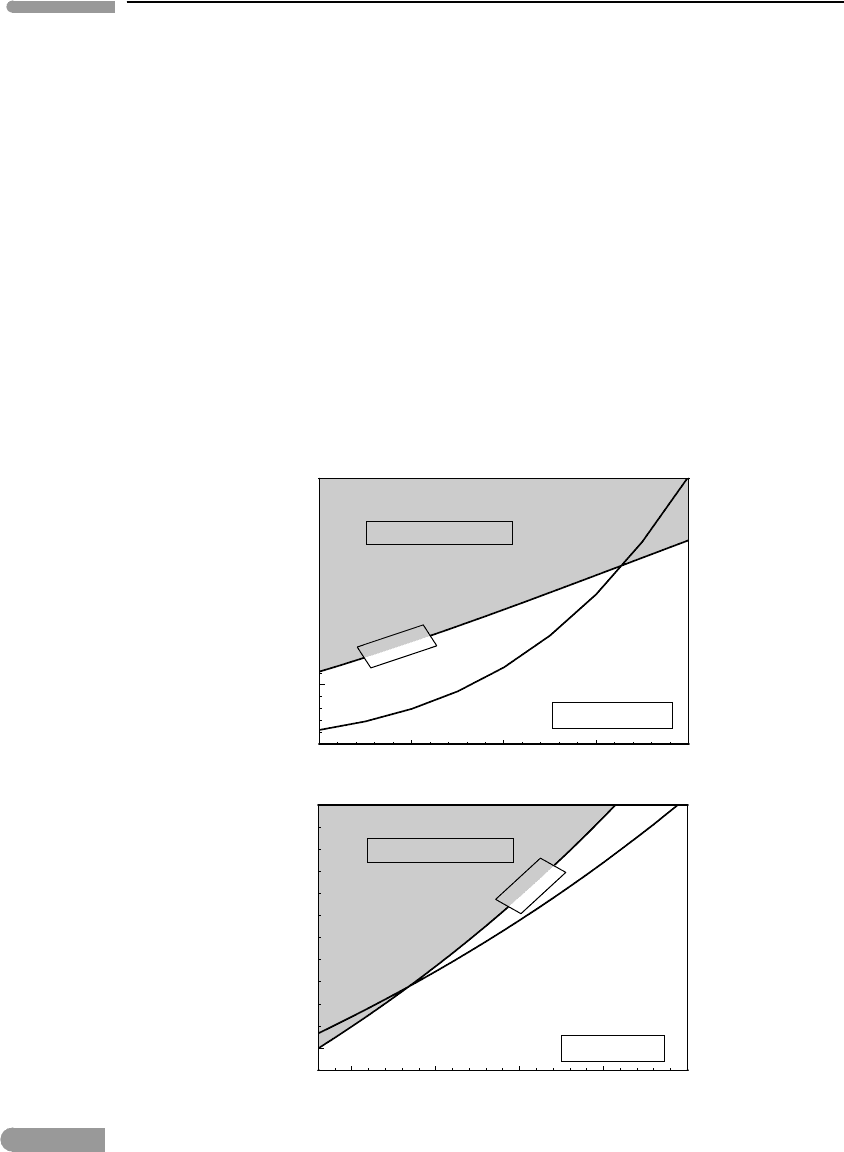
Fugacities of H

O calculated from (9.16) are shown in Fig. 9.1, as a function of temper-

ature at constant P = 6 kbar (top), and as a function of pressure at constant T = 500

◦

(bottom). By fixing one of these two intensive variables the curves in Fig. (9.1) become

pseudo-univariant phase boundaries (Section 6.3.1 ). Also shown in the figure are curves

showing the standard state fugacity of H

O, obtained by integrating (9.11) and substitut-

ing an explicit equation of state; this will be discussed later in this chapter. The standard

state fugacity curves separate a “feasible” region from a “prohibited” region, which is

shaded in the figure. The standard state fugacity of a fluid species, which is its fugacity

in a pure fluid, is the maximum value that fugacity can take at a given P and T. Fugacity

can be less than f

, but not greater. Equivalently, one can state that the chemical potential

at equilibrium cannot be greater than the chemical potential of the pure species, for if it

350 400 450 500 550

1000

2000

3000

4000

Temperature °C

f (H

O) bar

f (H

O) bar

4000 4500 5000 5500 600

1400

1600

1800

2000

2200

2400

Pressure bar

rhc

)

P = 6000 bar

T= 500°C

Prohibited region

Fig. 9.1 Calculated H

O fugacity along the forsterite–enstatite–chrysotile–vapor equilibrium, and standard state H

fugacity, at a constant pressure of 6 kbar (top) and constant temperature of 500

◦

C (bottom). A fugacity greater than

the standard state fugacity at the same P and T is not an equilibrium condition.

425 9.1 Fugacity and standard state fugacity

was then the pure phase would form, lowering the Gibbs free energy to that of the pure

species.

The curves for f (H

O) along equilibrium (9.15) intersect the f

O) curves. At the

intersection f (H

O)=f

O), so these points represent equilibrium in the presence of

a fluid composed of pure H

O. The intersections in Fig. 9.1 correspond to points on the

univariant equilibrium phase boundary for reaction (9.15). The segments of the f (H

curves that enter the “prohibited regions” represent impossible conditions. The H

O fugac-

ity curves must therefore terminate at the f

O) curves, but are shown in the figure

extending beyond the intersection for the sake of this discussion. The figures can also be

interpreted as saying that chrysotile is not stable at temperatures greater than, or pres-

sures less than, those at the intersection, and that these intersections are the ultimate

limits of chrysotile stability (because it must be f (H

O)≤f

O)). On the opposite

side of the intersections the four-phase assemblage enstatite + forsterite + chrysotile

+ fluid is stable, and the fugacity of H

O lies on the pseudounivariant phase bound-

ary. Because this fugacity is lower than the standard state fugacity, however, a pure H

fluid cannot be present at equilibrium. If a fluid is present then the distance between the

two curves is a measure of the H

O content of the fluid in equilibrium with the three

solid phases.

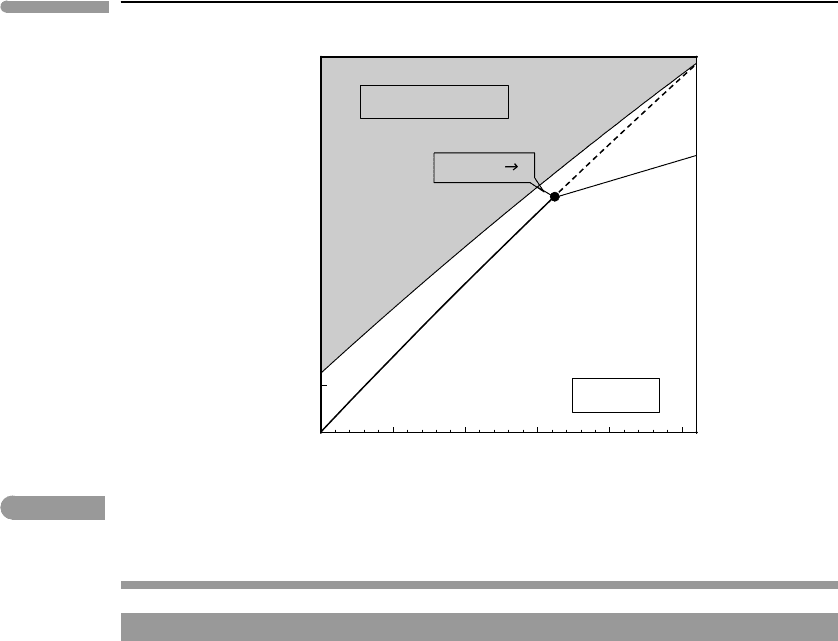
Worked Example 9.2 Evaporites revisited

Let us take another look at the thernardite–mirabilite equilibrium that we discussed in

Chapter 6. In Fig. 6.13 we showed the phase relations as a function of the coordinates µ

and T. Equation (9.13) allows us to represent the chemical potential as a fugacity, but in order

to calculate actual fugacity values it is necessary to know standard state thermodynamic

properties (see equation (9.16)). These are known for the two crystalline phases but not for

the liquid. We can therefore calculate the position of the liquid-absent equilibrium only.

Using equation (9.16) and standard state properties from Robie and Hemingway (1995)we

calculate the univariant equilibrium curve at 1 bar shown in Fig. 9.2, which is the same as

Fig. 6.13. Calculated H

O fugacities are of order 10

−2

–10

−1

bar at T ∼20–40

◦

C. Because

I used standard state properties for H

O gas, these are the fugacities of H

O gas. At these

P –T conditions (ideal gas limit) fugacity is equivalent to the partial pressure of H

O. The

calculated fugacity can therefore be compared to the vapor pressure of H

O, i.e. to the partial

pressure of H

O vapor in equilibrium with its liquid (see Section 6.5.2 ). Saturation vapor

pressure is shown in the figure by the thin curve bounding the shaded “prohibited region”.

Equilibrium fugacities (or partial pressures) inside this region are impossible because liquid

O condenses and buffers the chemical potential of H

O, and f (H

O), at the saturation

vapor pressure. The thenardite–mirabilite phase boundary intersects the vapor saturation

curve at a temperature of ∼42

◦

C, meaning that the (pseudo)invariant point in Fig. 6.13 must

be located at a temperature lower than this. In Fig. 9.2 I show it at T ∼ 32

◦

C, which is its

approximate location as determined by phase equilibrium experiments (Rodríguez-Navarro

et al., 2000; Marliacy et al., 2000). The metastable extension of the liquid-absent reaction

is shown projecting to its intersection with the vapor saturation curve. The other two phase

boundaries are shown schematically. The precise conditions for the formation of thenardite

vs. mirabilite can be obtained from the diagram, with partial pressure converted to relative

humidity if desired.

426 Thermodynamics of planetary volatiles

15 20 25 30 35 40

–1.8

–1.6

–1.4

–1.2

Temperature °C

log

f(H

O) bar

mirabilite

thenardite + H

+ H

mi + H

O L

Prohibited region

P=1bar

Fig. 9.2 Calculated H

O fugacity along the thenardite–mirabilite equilibrium at 1 bar. The locations of the thenardite–liquid

and mirabilite–liquid equilibria are only approximate. Condensation of liquid H

O occurs along the boundary of the

“prohibited region”, which maps the saturation vapor pressure of H

Worked Example 9.3 Oxygen fugacity along iron oxidation reactions

The multiple oxidation states of iron: Fe

,Fe

, and its very large cosmic abun-

dance give this element the capability of serving as an oxygen buffer in many planetary

environments. Increasingly oxidized states of Fe can be related by the following three reac-

tions, conventionally called QFI (quartz–fayalite–iron), QFM (quartz–fayalite–magnetite)

and HM (hematite–magnetite), respectively:

2Fe +SiO

→

←

SiO

(9.17)

3Fe

SiO

→

←

2Fe

+3SiO

(9.18)

4Fe

→

←

6Fe

. (9.19)

Using equation (9.16) it is a simple exercise to calculate f(O

) −T curves for the three

reactions, which are shown for a constant pressure of 1 bar in the top panel of Fig. 9.3

(note that, with the exception of fayalite, all solid phases in these reactions undergo lambda

phase transitions, whose free energy contributions must be included in equation (9.16), as

we discussed in Section 7.6). The thermodynamic meaning of the f(O

) −T curves is the

same as that of the chrysotile dehydration curves in Fig. 9.1: as long as a given solid phase

assemblage is present oxygen fugacity is buffered at the values along the corresponding

curve.There are a couple of important differenceswith the serpentinization example,though.

First, because oxygen fugacity values are many orders of magnitude smaller than 1, it is not

necessary to worry about the standard state fugacity of oxygen, as the curves stay well within

the “feasible” region. This is another way of saying that oxygen has a strong affinity for

most other elements, so that one is unlikely to come across oxygen in a state approaching its

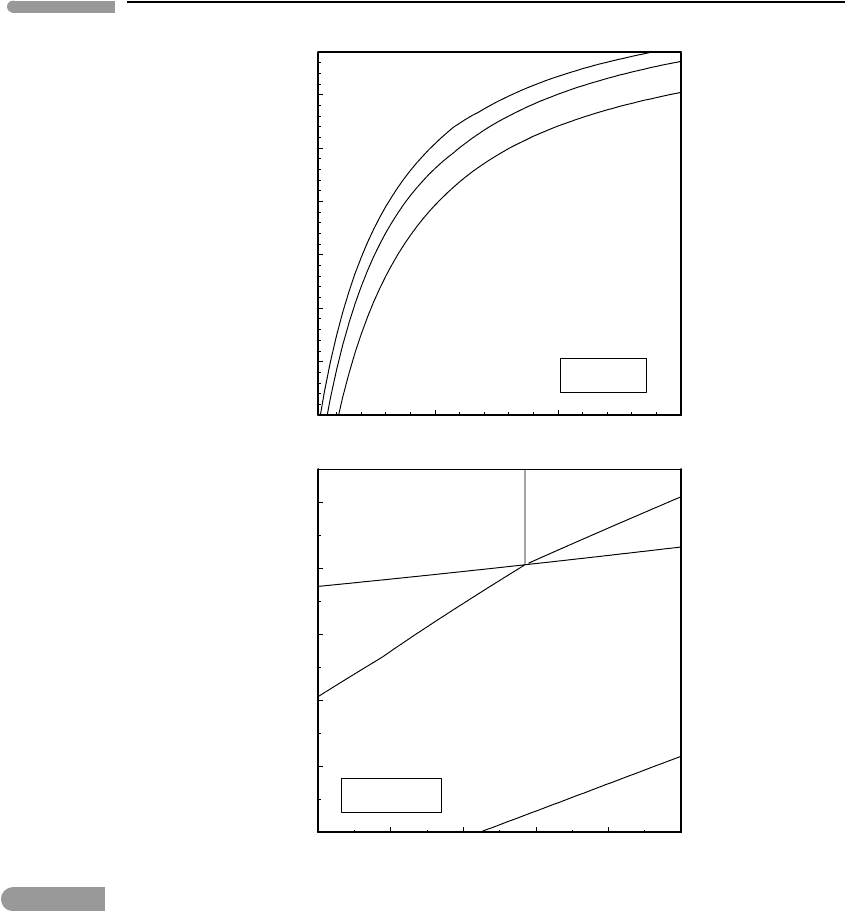
427 9.1 Fugacity and standard state fugacity

500 1000 150

–70

–60

–50

–40

–30

–20

–10

Temperature °C

020406080100

–14

–12

–10

–8

–6

–4

Pressure kbar

tq z

ztq

P=1 bar

T = 1000°C

+ ztq

ztq

tmq+ zt

mhf+a

log

f (O

) bar

log

f (O

) bar

Fig. 9.3 Top: oxygen fugacity as a function of temperature along three successive Fe oxidation reactions, at P =1 bar.

Bottom: oxygen fugacities along Fe oxidation reactions as a function of pressure, at T = 1000

◦

standard state. Oxygen fugacity in the terrestrial atmosphere, ∼0.2 bar, is not at equilibrium

with the Earth’s surface, but makes it possible for me to write this and for you to read it. I

discuss this topic in Chapter 14. Second, in the case of the chrysotile dehydration reaction it

is possible, but not necessary, to give the H

O fugacity values an interpretation in terms of

mol fraction of H

O in a fluid (more on this later in this chapter). For oxygen fugacities such

as those in Fig. 9.3 this interpretation becomes problematic, as we already noted. Oxygen

fugacity along buffering reactions such as those in Fig. 9.3 must be seen as a measure of the

chemical potential of O

, independently of whether or not a fluid phase exists at equilibrium

with the solid phases. This same interpretation is of course also valid for H

O fugacities

in Fig. 9.1 and 9.2, but in those cases we can also make meaningful inferences about fluid

composition, assuming that a fluid phase exists.