Douce A.P. Thermodynamics of the Earth and Planets

Подождите немного. Документ загружается.

508 Melting in planetary bodies

0 20 40 60 80 100

0.1

0.2

0.3

0.4

Pressure (kbar)

020406080

100

Pressure (kbar)

Melt fraction

1300

1400

1500

1600

1700

1800

1900

Temperature (°C)

Melting in the Martian mantle

= 1800°C

Thin lithosphere

=1500°C

Thick lithosphere

=1800°C

= 1500°C

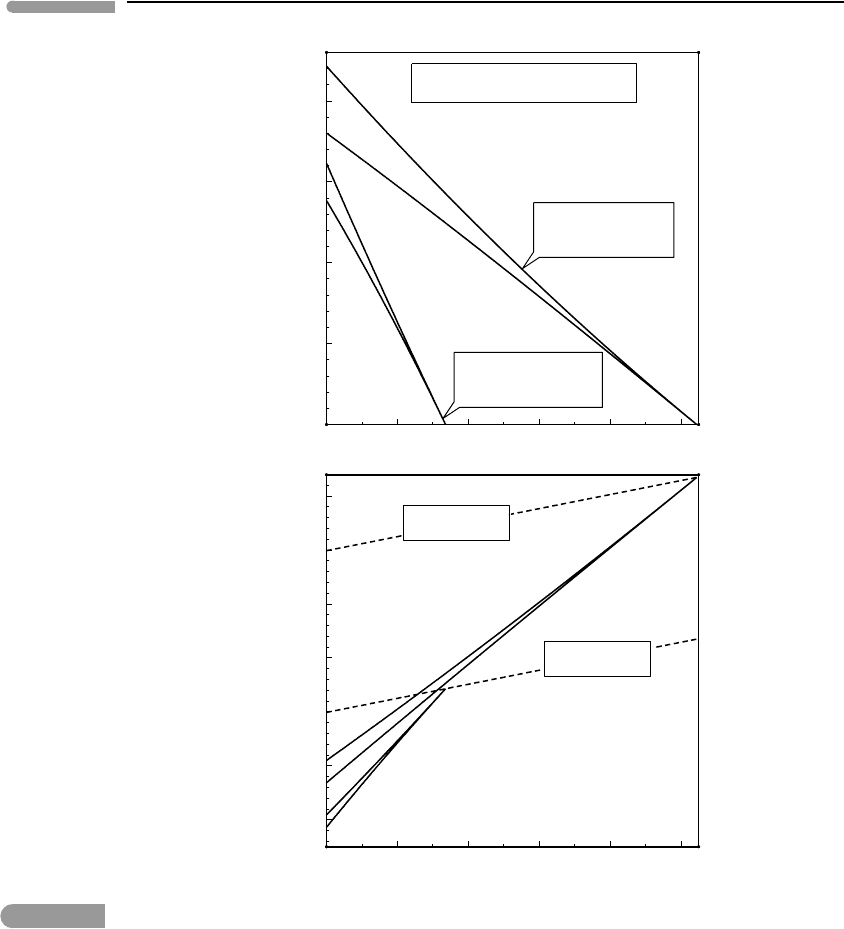
Fig. 10.13 Melt generation in the Martian mantle, assuming either a 700 km lithospheric lid capping an adiabatic mantle with

=1500

◦

C, or a 250 km thick lithospheric lid over an adiabatic mantle with T

=1800

◦

C. Envelopes spanning

batch melting to fractional melting are shown in both cases. Melting in the thin lithosphere model begins within the

asthenosphere and is probably inconsistent with the lack of planet-wide volcanism. Melting in the thick lithosphere

model would begin well within the lithosphere, and would only be made possible by the existence of large and

long-lived mantle plumes. This may be the reason why only two large and isolated young volcanic provinces, Tharsis

and Elysium, exist on Mars.

As a first approximation, then, we will assume that these quantities stay constant along each

decompression path, but choose different Clapeyron slopes, of 80 and 130 bar K

−1

for the

melting paths beginning at 34 and 105 kbar, respectively.

The calculated decompression melting paths are shown in Fig. 10.13, as a function of

pressure in the Martian interior (not P, compare Figs. 10.11 and 10.12). Envelopes are

509 10.6 Decompression melting

shown for each adiabat, spanning the range between batch and fractional melting. The

pressure at the bottom of a 700 km thick Martian lithosphere is approximately 86 kbar. If

the potential temperature of the underlying convective mantle is 1500

◦

C melting would

begin at a pressure of ∼34 kbar, or more than halfway across the lithosphere. In other

words, the asthenosphere must be able to penetrate some 400 km of lithosphere before

it starts melting. One could expect that volcanic activity in this model would be sparse,

and limited to places where large and very long-lived hot spots are capable of transferring

enough heat to “thermally drill” through the lithosphere. If a decompression melting regime

can be established melt fractions of up to about 30% would be achieved, and the magmas

could have eruption temperatures of at least 1300

◦

C (higher if magmas are segregated

at depth). A hotter Martian mantle, with a potential temperature of 1800

◦

C, would start

melting at about 105 kbar. The pressure at the bottom of the 250 km lithosphere capping

that mantle would be about 30 kbar. Melting in this case would be widespread, and melt

fractions of 40% or higher would not be uncommon.

Although the results shown in Fig. 10.13 are only rough approximations, the qualitative

distinction between the magmatic activity that is to be expected from the two Martian mantle

models is probably robust. The thick lithosphere model is consistent with the existence of

few, large and long-lived magmatic provinces, which is what is observed in Mars. The thin

lithosphere would generate a much more volcanically active planet than is observed.

I wish to emphasize that the equations and numerical examples presented in this section

are extremely simplified pictures of decompression melting in nature. They are only

intended to convey the thermodynamic underpinnings of the process, and in that sense

I believe that their simplicity is hard to argue with. The fundamental physics are contained

in the equations, even if they cannot provide any petrological detail. Thorough mathemat-

ical and numerical treatments of decompression melting in real muticomponent systems

have been presented, among others, by McKenzie (1984), McKenzie and Bickle (1988,

and most recommended), Iwamori et al. (1995), Asimow and Stolper (1999) and Asimow

(2002). The reader is urged to consult these works for what is missing above.

10.6.5 Departures from the constant-entropy assumption

During fractional decompression melting heat loss from the magma source region lessens

melt production relative to batch melting. There are other reasons why the results of the

previous sections, which assume either global or local isentropic conditions, may have to

be revised. For example, we may ask, what must be the size of the region undergoing

decompression melting so that diffusive heat loss can be safely ignored, i.e. so that the

system is truly adiabatic? If diffusive heat loss is not negligible then melt production will

be lower than that predicted by the equations derived above. We may also wonder whether

the melting region is isentropic, even if it is adiabatic. If energy dissipation takes place

inside an adiabatic system then dS > 0, and in this case melt production will be higher than

what those equations predict. We can generate order of magnitude estimates for some of

these effects.

For the sake of expository synthesis I will call the ascending region of the mantle that

undergoes decompression melting a “diapir”, without necessarily implying that I know what

a diapir is, nor that there is consensus that diapirs as envisioned by Ramberg (1967) exist. We

can estimate the effect of diffusive heat exchange between the diapir and its environment by

510 Melting in planetary bodies

means of the Péclet number (Section 3.6.2), and we can do this in two ways. First, consider

vertical heat flow, i.e. in the same direction that the diapir is moving. Figure 10.7 shows

that the characteristic depth at which melting begins under mid-ocean ridges is of order 50

km. Using this value for M in equation (3.46), assuming u =5cmyr

−1

≈1.6 ×10

−9

−1

and κ = 10

−6

−1

we get Pe≈ 80. Thus, mantle upwelling is 80 times more efficient

than diffusion in transporting heat in the direction in which progressive melting takes place,

which says that we are justified in considering the system adiabatic in this direction. But

what about horizontal heat diffusion? Equation 3.48 relates the lengthscale of advective

heat transfer (M) to the lengthscale of diffusive heat transfer in a direction perpendicular

to advection (λ). This can be applied to a situation in which hot asthenosphere penetrates,

and is surrounded by, colder lithosphere (Fig. 10.7). Substituting the definition of Péclet

number (equation (3.46)) in (3.48) we obtain:

λ ∼2



Mκ



1/2

. (10.42)

As before, M is the depth at which decompression melting begins (∼50 km), as this is the

distance over which the thermal perturbation caused by melting will develop. With the same

values of u and κ as before we find λ ≈ 50 M

1/2

, for λ and M in meters. We can expect

heat diffusion to affect an approximately 10 km wide rind of a 50 km tall diapir. Thus, if

the diapir is at least a few tens of km wide, then its outer part may cool down significantly,

but there will always be a core region in which the assumption of adiabatic behavior is

warranted. If adiabatic upwelling continues for an extended period of time, moreover, then

the environment will heat up, decreasing the horizontal thermal gradient and hence the rate

of heat loss. It is significant that λ goes as the square root of M. For example, if melting

occurred at the base of the thick Martian lithosphere (∼700 km) a diapir would have to be

some 3–4 times wider than under Earth’s oceans in order to be able to generate eruptable

magmas. The size of the Tharsis and Elyseum volcano-tectonic bulges (1000–5000 km)

suggests that Martian mantle plumes were (are?) larger than Earth’s.

Sources of energy dissipation inside an adiabatically rising diapir include: inelastic rock

deformation, dissipation of gravitational potential energy by separation of melt and solid

of different densities, viscous flow of melt, radioactive heating and chemical diffusion. We

will examine only the first two processes (see Asimow, 2002, for a complete mathematical

treatment of all of them). We seek equations for the rate of entropy production with pressure,

(∂S/∂P )

. Because this entropy is generated inside the system, and the system is still

assumed to be adiabatic, there is no entropy exchange with the environment, and we can

modify equation (10.25) as follows:

dT +





∂S

∂P



−αV



dP +

Sdϕ = 0. (10.43)

We derived equation (1.83) to quantify frictional heating in a fault or shear zone, but it can

also be applied to estimate energy dissipation by inelastic deformation inside a diapir. Let

us re-write (1.83) as follows:

τV

, (10.44)

where τ is the magnitude of the shear stress that causes deformation in the diapir, z is the

width over which inelastic strain is distributed, V is the molar volume of the material and

511 10.6 Decompression melting

its molar heat capacity (equation (1.83) is written in terms of density and specific heat,

but in the present discussion I find it simpler to use molar quantities). Because dx is a

displacement in the direction in which the shear stress is applied, and shear stress in an

ascending diapir is chiefly vertical, we can interpret the ratio dT /dx as the vertical thermal

gradient engendered by viscous dissipation. We seek to convert this into a rate of entropy

production with pressure, so, using the chain rule:



∂S

∂P



. (10.45)

Writing the condition of hydrostatic equilibrium (equation (3.34)) in terms of molar

properties and using (1.3.18) we get :

, (10.46)

where m is the molecular weight of the material. Recalling that (∂S/∂T )

= C

/T ,

equation (10.45) becomes:



∂S

∂P



τV

zTgm

. (10.47)

For olivine we have V ≈4.5×10

−5

mol

−1

and m ≈0.14 kg mol

−1

. Characteristic values

for the other parameters for Earth’s upper mantle are τ ≈ 10

bar = 10

Pa, T ≈ 1600 K

and g = 9.8ms

−2

. These values yield (∂S/∂P )

≈ 900/z JK

−1

kbar

−1

mol

−1

, with

z in meters. If strain is distributed evenly over the width of the diapir, then for a 50 km

wide diapir (∂S/∂P )

≈0.02 J K

−1

kbar

−1

mol

−1

. By comparison, the product αV is of

order 0.2 J K

−1

kbar

−1

mol

−1

, i.e. one order of magnitude greater. These two terms are

combined in equation (10.43), so we can conclude that the contribution of inelastic rock

deformation to melt production averaged over the entire volume of the diapir is likely to be

small. However, if strain is focused on narrow shear zones (small z) then viscous heating

may be locally important and greatly enhance melt production in the shear zones.

Dissipation of gravitational potential energy can take place inside a diapir if the melt,

which is less dense than the solid, ascends relative to the latter. We can estimate the thermal

effect of gravitational melt segregation as follows. Consider an infinitesimal vertical interval

of the diapir of length dx. A volume V

of melt ascends this distance, displacing an equal

volume of solid which sinks the same distance. The amount of gravitational energy that is

dissipated, dU

, is given by:

ρgdx, (10.48)

where ρ is the difference in density between melt and solid and g is gravitational accel-

eration. The gravitational potential energy dissipated per unit volume of rock, dU

g,V

, must

clearly attain its maximum value when the rock is 50% molten. We can then write:

g,V

=ϒρgdx, (10.49)

where the parameter ϒ is defined as follows. Let ϕ be the volume fraction of melt. Then

ϒ = ϕ if ϕ ≤ 0.5, and ϒ = 1 −ϕ if ϕ>0.5. Since gravitational energy is dissipated as

thermal energy we can also write:

g,V

dT =

ρC

dT , (10.50)

512 Melting in planetary bodies

where C

,V and m are molar properties, and dQ

g,V

is heat generated per unit volume.

Equating (10.49) and (10.50) we get:

=ϒ

ρ

(10.51)

and, by using (10.45) and (10.46):



∂S

∂P



=ϒ

ρ

. (10.52)

For olivine at mantle conditions V/T ≈2.8JK

−1

kbar

−1

mol

−1

. Now,because (10.52) takes

its maximum value for ϕ =0.5, we have (∂S/∂P )

pr,max

≈1.4(ρ/ρ) JK

−1

kbar

−1

mol

−1

For this term to be comparable to αV ≈ 0.2JK

−1

kbar

−1

mol

−1

it must be ρ/ρ ≈ 0.14,

or, for a solid density of 3300 kg m

−3

, ρ ≈ 500 kg m

−3

, which is about the same as

the difference in density between basaltic melt and peridotite. Dissipation of gravitational

energy by phase separation could thus make a non-negligible contribution to melt production

but only when melt fraction in the diapir approaches 50%, and assuming that there is

complete separation of the two phases. Even in this case the effect of phase separation would

only be enough to cancel out the expansion term, αV (see equation (10.43)), which itself

is about one fifth the magnitude of the cooling term (equations (10.29)). One can conclude

that under most circumstances the isentropic model of melt production (equation (10.25))

is a reasonably good approximation to decompression melting in planetary mantles.

10.7 Open system melting

At the other end of the spectrum from isentropic decompression melting is open system

melting, in which the system is open to influx of mass, typically in the form of a fluid phase,

and energy. The simplest example of this is a two-component system with a binary melt

phase, in which one of the components makes up a pure solid phase and the other component

a pure fluid phase. This system will allow us to look at the fundamental thermodynamic

and physical aspects of fluid-fluxed melting. The three phases, solid, fluid and melt, con-

stitute a univariant assemblage or, at constant pressure, a pseudoinvariant assemblage. This

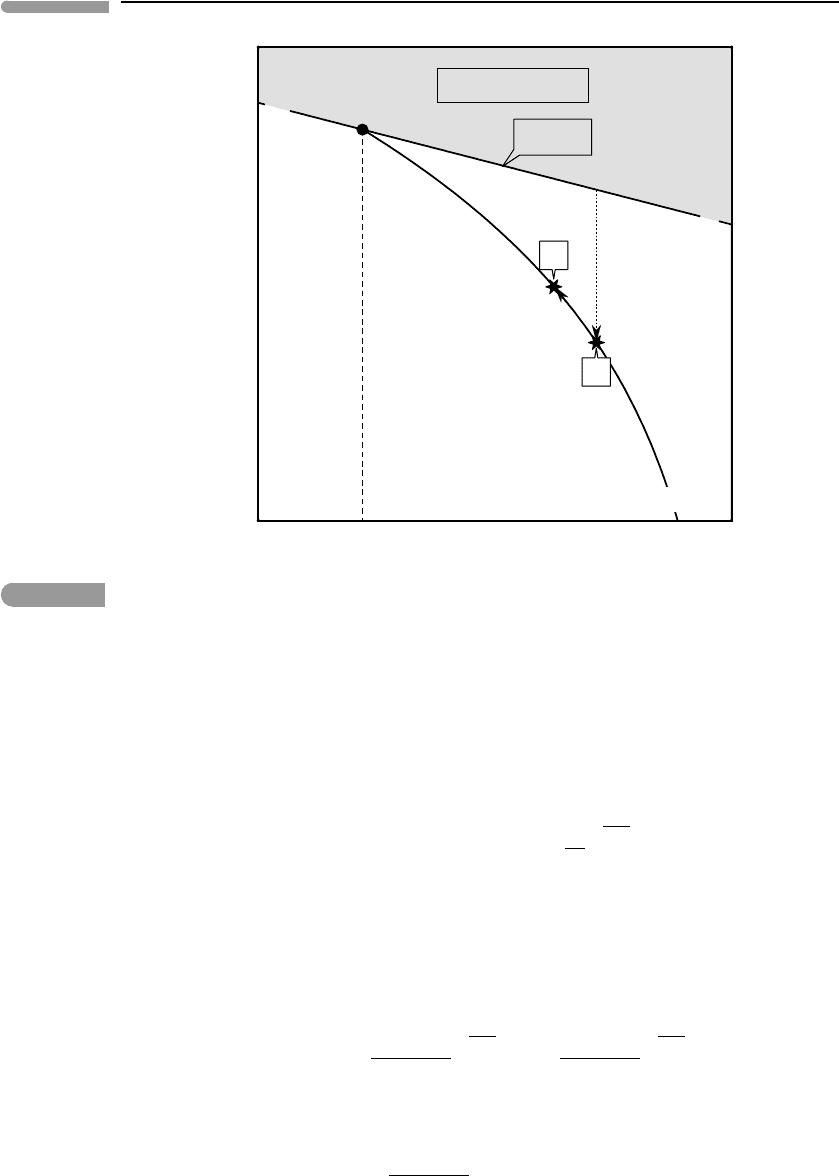
assemblage exists at equilibrium at point I in Fig. 10.14, a schematic isobaric diagram in

which the coordinates are the chemical potential of the fluid component and temperature.

The curve that traces the chemical potential of the pure fluid component (µ

0,fluid

) bounds

a “prohibited region”, as the system cannot exist at equilibrium for µ

fluid

> µ

0,fluid

. The

two branches of this curve correspond to the pseudounivariant equilibrium assemblages

melt + fluid (=solid absent) and solid + fluid (= melt absent), at temperatures higher and

lower than that of the pseudoinvariant point, respectively. The vapor-absent melting curve,

corresponding to the equilibrium assemblage solid + melt, connects the pseudoinvariant

point with the melting point of the pure solid (T

) in the fluid-free system.

The mol fraction of fluid component in the melt is the variable X

z,m

in the melting point

depression equation (10.16). Assuming ideal mixing in the melt the vapor-absent curve is

513 10.7 Open system melting

fluid

Prohibited region

Solid

Melt

Temperature

µ fluid

min

(v)

(m)

(s)

Fig. 10.14

Isobaric µ −T diagram for ﬂuid-ﬂuxed melting in a two-component system: solid +ﬂuid. Chemical potentials

higher than the standard state chemical potential of the pure ﬂuid are impossible at equilibrium. The three phases

solid +ﬂuid +ﬂuid-saturated melt exist at equilibrium at point I. The temperature of point I is the minimum

melting point of the system. Solid +ﬂuid-undersaturated melt exist along the vapor-absent curve, that ends at the

melting temperature of the ﬂuid-absent one-component system. Addition of a small amount of ﬂuid δm

causes a

small amount of solid δm

to melt. The temperature must drop from A to B to provide the necessary enthalpy of

melting.

then given by:

fluid

P ,T

=µ

0, fluid

(o)

+RT ln



1 −









. (10.53)

If, as is commonly the case, mixing is not ideal then the term in square brackets would be

multiplied by an activity coefficient, but the geometry of the diagram would not be affected.

The composition of the melt along the melt–solid coexistence curve (V ) is also obtained

from the melting point depression equation. Defining m

and m

as the number of mols

of molten solid and fluid contained in the melt, respectively, we have:

T = T



1 −











. (10.54)

The validity of this equation is limited by the solubility of the fluid at the conditions of

melting, X

saturation

, so that we require:

≤X

saturation

(10.55)

514 Melting in planetary bodies

where the saturation mol fraction X

saturation

depends on pressure, temperature and the

compositions of fluid and melt. When melt in equilibrium with solid becomes saturated in

the fluid component it must be µ

fluid

=µ

0,fluid

, so the fluid saturation point corresponds to

the pseudoinvariant point in Fig. 10.14. The temperature of this point defines the minimum

melting temperature of the system at the pressure of the diagram.

We now add the energy conservation condition to the phase relations. Say that we have

a system consisting of melt and solid at equilibrium at point A in the figure. The system

is invaded by a small amount of fluid, δm

, which for simplicity we will assume is at

the same temperature as the system (we will address possible differences in temperature

shortly). Because the chemical potential of the pure fluid is higher than that of the fluid com-

ponent in the melt the added fluid must dissolve in the melt in order to restore equilibrium.

But the added fluid also lowers the equilibrium temperature for the solid + melt assemblage,

so that enthalpy must be released. The enthalpy is absorbed as enthalpy of melting, causing

a small amount of dry solid, δm

, to melt. Addition of δm

mols of fluid therefore causes

equilibrium to shift from point A to point B. The magnitude of this displacement, or equiv-

alently, the amount of solid that melts, δm

, is determined by two opposing factors: (i) the

melting point depression effect of the added fluid (equation (10.54)) and (ii) the energy

balance, which is given by the following equation:

P ,R

δT +T

Sδm

P ,F

(

T −T

)

δm

=0, (10.56)

where m

is the total number of mols in the system (solid + melt), T is the temperature after

equilibrium is restored (T of point B in the figure), δT is the temperature change required

to supply the enthalpy of melting (T

−T

), 

S is the entropy of melting, T

is the initial

temperature of the fluid, and C

P ,R

and C

P ,F

are the heat capacities of the system (which

for simplicity, and as in the case of decompression melting, we will assume to be constant

and independent of melt fraction and melt composition) and of the fluid, respectively.

Equations (10.54) and (10.56) can be solved iteratively for T and m

as a function of

, for both batch and fractional melting. We do that in the following numerical example,

but first let us see how the results from the two melting regimes are expected to differ.

Differentiating (10.54) we get:

=−T



R/

(

)

R/

S+1

. (10.57)

The variables m

and m

are related by a possibly variable factor k, which, however,

is always a finite (as opposed to infinitesimal) quantity. We can write m

= km

, and

substituting in (10.57) we arrive at:

∼−T



(

k +1

)

R/

S+1

R/

. (10.58)

Recall that m

is the amount of solid component present in the melt. This is a finite value

during batch melting, but tends to an infinitesimally small value during fractional melting.

Hence, the rate of change of temperature with added fluid along the vapor-absent curve in

Fig. 10.14 is greater during fractional melting than during batch melting. This implies a

greater enthalpy release and, therefore, for the same total amount of fluid added, greater

melt production for fractional melting than for batch melting. This behavior is opposite to

that of decompression melting of a dry solid.

515 10.7 Open system melting

Worked Example 10.3 Batch vs. fractional melting by fluid influx

Both batch melting and fractional melting can be thought of as being made up of a large

number of small increments. The difference between both processes is whether the succes-

sive melt increments, δm

, stay in the system (batch) or leave (fractional). Let T

i−1

be the

equilibrium temperature of the system at the end of an incremental melting step. Substitut-

ing (10.54)in(10.56) and simplifying we can write the energy balance for the subsequent

melting increment as follows:



P,R

+

Sδm

P ,F

δm









−C

P,R

i−1

−C

P,F

δm

=0.

(10.59)

The idea now is to solve equations (10.59) and (10.54) iteratively for δm

and T by adding

small fluid increments δm

. This can be done with a simple Maple procedure (Software

Box 10.2). It is convenient to define two new variables, the total amount of dry rock that has

melted after (i −1) fluid increments, D

(i−1)



(i−1)

δm

, and the total amount of fluid

added to that point, F

(i−1)



(i−1)

δm

. The solutions for batch and fractional melting

are different from this point on.

Software Box 10.2 Calculation of volatile-fluxed melting

The Maple worksheet volatile_melting.mw contains the procedures

volatile_ batch_melting and volatile_fractional_melting, that

calculate melt production by volatile infiltration. The procedures solve equation (10.59)

for small melt increments, δm

, and then calculate temperature with equation (10.54).

The algorithms for batch and fractional melting are explained in Worked Example 10.3.

The procedure call requires that one specify the initial temperature of the rock, T

and the temperature of the fluid, T

, both in Kelvin, and a filename for the output.

Other model parameters can be changed by editing the procedures, following the same

conventions discussed in Software Box 10.1. The variable dfluid specifies the added

amount of fluid at each step, δm

(in mols per mol of rock).

The procedures generate text files in which each line gives the state of the system

after addition of each fluid increment. There are six output fields, as follows. The first

field is the total amount of fluid added, the second is the total amount of solid that has

melted, the third is the temperature (in Kelvin), the fourth is the mol fraction of fluid in

the melt, the fifth is the size of the system, i.e. initial solid plus added fluid for batch

melting, or initial solid minus melt produced for fractional melting, and the sixth field

is the melt increment generated at each step, δm

The procedures iterate 2000 times (this can be changed by editing the do loop) and

do not check whether the mol fraction of fluid dissolved in melt (the fourth output

field) exceeds the likely solubility. One can examine the output and discard whatever

portion of it implies unreasonable volatile solubility.

Let us assume that we start with 1 mol of dry solid. During batch melting the melt,

including the fluid dissolved in it, stays in the system, so we make m

=1 +F

(i−1)

+δm

(recall that m

is the total size of the system). Using the same argument we can see that for

516 Melting in planetary bodies

the batch melting case the melt composition in the melting point depression

equations (10.59) and (10.54) is given by m

= D

(i−1)

+δm

and m

= F

(i−1)

+δm

Choosing some small value for δm

and making T

i−1

equal to the value of T calculated

in the previous step we solve equation (10.59) for δm

, and then (10.54) for T . In the case

of fractional melting the fraction of solid that melts, and the fluid dissolved in it, leave the

system, so we make m

= 1 −D

(i−1)

. As none of the melt previously formed remains in

the system, in this case we make m

=δm

and m

=δm

. As before, we specify a small

value of δm

and solve (10.59) for δm

, and then (10.54) for T (Software Box 10.2).

We can study the behavior of these equations by choosing characteristic values for the

parameters, as follows: C

P,R

=200JK

−1

mol

−1

(a decent guess for Mg silicates), C

P ,F

50JK

−1

mol

−1

(a ballpark figure for H

O) and 

S = 56JK

−1

mol

−1

(the value for

forsterite). Let us also make T

=1600 K (a characteristic upper mantle temperature,

which we assume to be also equal to the temperature of the fluid, T

), and note that, given

that the heat capacity of the fluid is only one fourth that of the rock and the total amount

of fluid added is well below 1, the solution is not likely to be very sensitive to our choice

of T

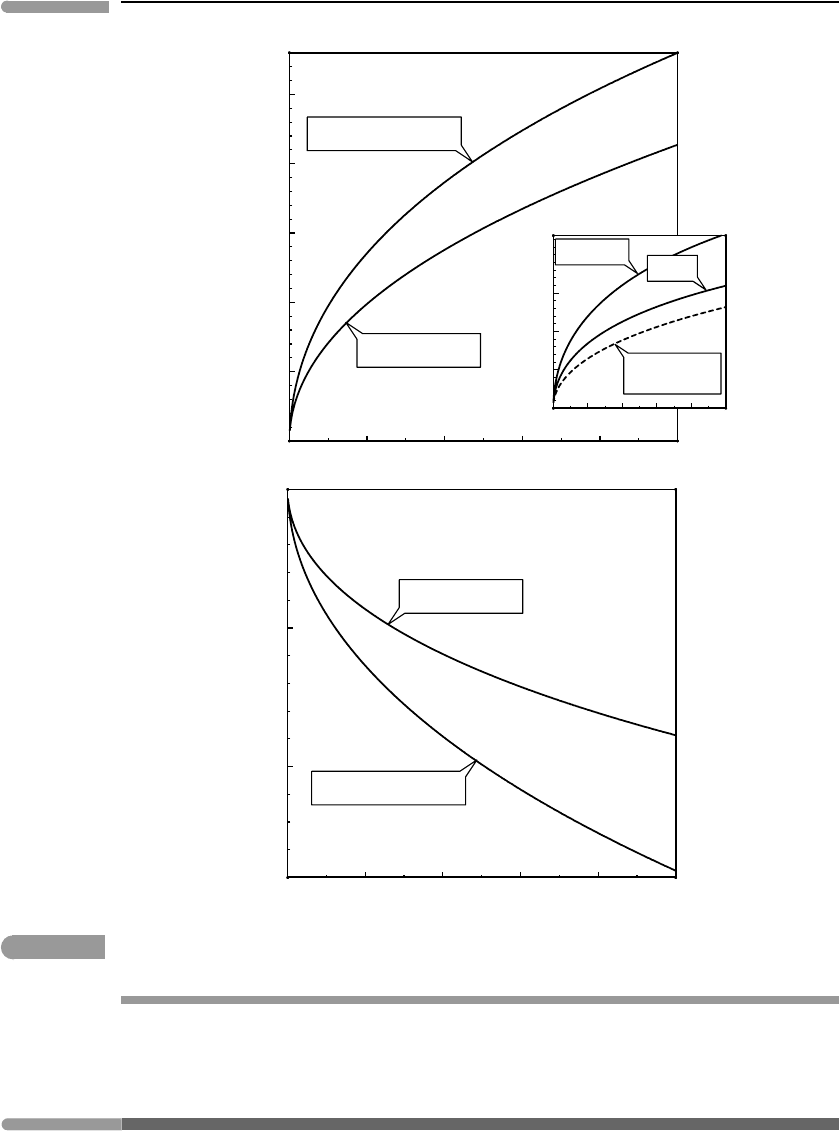
. Figure 10.15 shows calculated total melt production (i.e. the fraction of solid that

has melted) and melting temperature as a function of the total amount of added fluid, up to

0.1 mol per mol of solid rock.

As expected, our simple model for fluid-fluxed melting produces more melt by fractional

melting than by batch melting. The difference is considerable: about 28% of the rock

melts during fractional melting, versus some 23% during batch melting. For both batch

and fractional melting it is clear that, if the solubility of the fluid in the melt is sufficiently

high, then fluid-fluxed melting is an efficient mechanism of magma generation. Between

20 and 30 molar% of dry solid melts by addition of ∼0.1 mols of fluid to 1 mol of solid.

Solving equation (10.19) for the mass proportion of fluid, C

fluid

, and assuming that the ratio

of molecular weights is M = 10 (a possible value for H

O and Mg silicates) we find that

0.1 mol of H

O added to 1 mol of silicate rock corresponds approximately to 1 wt% H

The inset in Fig 10.15 shows the calculated mol fraction of fluid in the melts. The solid

curve for fractional melting shows the fluid concentration in each small melt increment,

whereas that for batch melting shows fluid concentration in the total amount of melt gen-

erated. The equivalent curve for fractional melting is shown with a dashed line, and is of

course below that for batch melting, as it must given that the total amount of melt produced

is greater (there is an apparent contradiction here that is not such, see Exercise 10.7). The

mol fraction of fluid in melts produced with the addition of 0.1 mols of fluid is ∼0.32

for batch melting (total melt) and ∼0.45 for fractional melting (last melt increment). For

M =10 this would correspond to ∼4.5 wt% and 7.6 wt%, respectively, which is well below

O solubility at mantle pressures. This calculation is admittedly very crude, but even if

the ratio M were ∼2 (an unlikely low value for H

O in silicate melts) we would get fluid

concentrations of 19 and 29 wt%, respectively, which are comparable to H

O solubility in

silicate melts at upper mantle pressures.

Of course, this calculation is highly simplified and completely ignores the phase equi-

librium of melting in complex natural systems. It also ignores effects such as that of excess

Gibbs free energy of mixing in the melt, which might cause an even stronger depression of

the solidus and potentially supply a greater amount of enthalpy of melting. Recall, finally,

that this calculation assumes that the initial temperature of the rock is the dry solidus. Melt

production would be less if the rock’s initial temperature is lower. Despite these simplifi-

cations the calculations expose the fundamental physical aspects of fluid-fluxed melting,

and demonstrate the importance of a process without which melting at Earth’s convergent

plate margins would be virtually impossible.

517 10.8 The nature of solid–melt equilibrium

0 0.02 0.04 0.06 0.08 0.1

0.05

0.1

0.15

0.2

0.25

Added fluid (mols per mol of rock)

Mol fraction of solid melted

Temperature (K)

1500

1550

1600

0 0.02 0.04 0.06 0.08 0.1

0.1

0.2

0.3

0.4

diulf

nitlem

Fractional melting

Batch melting

Fractional

Batch

Fractional

(cumulative)

Fractional melting

Batch melting

Fig. 10.15 Batch and fractional melting of a two-component system: solid +ﬂuid. The calculation assumes that the solubility of

the ﬂuid in the melt is at least as high as the maximum X

ﬂuid

values shown in the inset diagram.

10.8 The nature of solid–melt equilibrium in icy satellites

In Worked Example 6.10 we discussed how methane–carbon monoxide cryomagmas could

form in outer Solar System objects. In less extreme worlds, such as the moons of Jupiter and

Saturn, cryomagmatism is more likely to be based on water. A distinct property of water is