Доспехов Б.А. Методика полевого опыта

Подождите немного. Документ загружается.

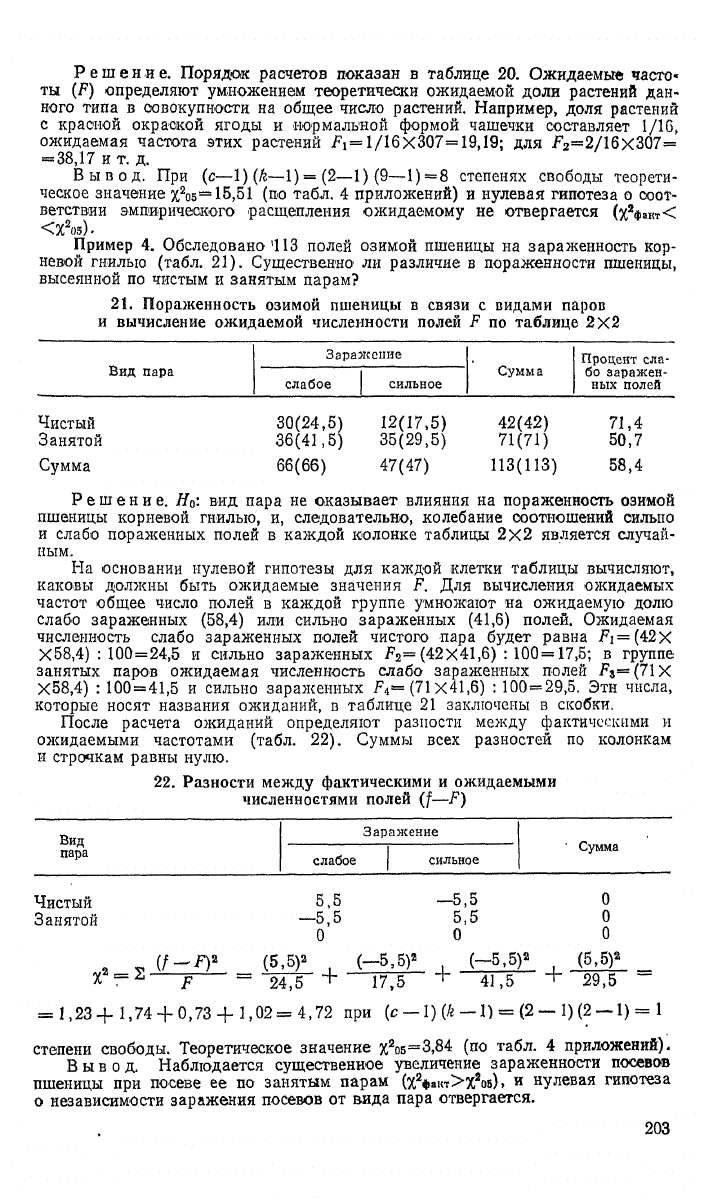
Решение. Порядок расчетов показан в таблице 20. Ожидаемые часто-

ты (F) определяют умножением теоретически ожидаемой доли растений дан-

ного типа в совокупности на общее число растений. Например, доля растений

с красной окраской ягоды и нормальной формой чашечки составляет 1/16,

ожидаемая частота этих растений Л= 1/16x307=19,19; для F

==2/16x307=

= 38,17 и т. д.

Вывод. При

(с—

1) (k~-l) = (2—1) (9—1)=8 степенях свободы теорети-

ческое значение

os= 15,51

(по табл. 4 приложений) и нулевая гипотеза о соот-

ветствии эмпирического расщепления ожидаемому не отвергается (%

кт<

<Х

ов).

Пример 4. Обследовано 113 полей озимой пшеницы на зараженность кор-

невой гнилью (табл. 21). Существенно ли различие в пораженности пшеницы,

высеянной по чистым и занятым парам?

21.

Пораженность озимой пшеницы в связи с видами паров

и вычисление ожидаемой численности полей F по таблице 2X2

Вид пара

Чистый

Занятой

Сумма

Заражение

слабое сильное

30(24,5) 12(17,5)

36(41,5) 35(29,5)

66(66) 47(47)

Сумма

42(42)

71(71)

113(113)

Процент сла-

бо заражен-

ных полей

71,4

50,7

58,4

Решение. Я

: вид пара не оказывает влияния на пораженность озимой

пшеницы корневой гнилью, и, следовательно, колебание соотношений сильно

и слабо пораженных полей в каждой колонке таблицы 2x2 является случай-

ным.

На основании нулевой гипотезы для каждой клетки таблицы вычисляют,

каковы должны быть ожидаемые значения F. Для вычисления ожидаемых

частот общее число полей в каждой группе умножают на ожидаемую долю

слабо зараженных (58,4) или сильно зараженных (41,6) полей. Ожидаемая

численность слабо зараженных полей чистого пара будет равна ^1=(42х

Х58,4) : 100=24,5 и сильно зараженных F

= (42X41,6) : 100=17,5; в группе

занятых паров ожидаемая численность слабо зараженных полей F

=(71X

Х58,4) : 100=41,5 и сильно зараженных F

= (71X41,6) :

100

29,5.

Этн числа,

которые носят названия ожиданий, в таблице 21 заключены в скобки.

После расчета ожиданий определяют разности между фактическими и

ожидаемыми частотами (табл. 22). Суммы всех разностей по колонкам

и строчкам равны нулю.

22.

Разности между фактическими и ожидаемыми

численностями полей (f—F)

Вид

пара

Заражение

слабое

Сумма

Чистый

Занятой

= 2

if-f)

(5,5)

5,5

-5,5

•

-5,5

5,5

(—5,5)

(-5,5)'

(5,5)

F ~ 24,5 т 17,5 "г

41,5 т 29,5 ~

1,23+1,74

+ 0,73 +

1,02=4,72

при (с -1) (k -1) = (2 — 1) (2 —

= 1

степени свободы. Теоретическое значение %

о5=3,84 (по табл. 4 приложений).

Вывод. Наблюдается существенное увеличение зараженности посевов

пшеницы при посеве ее по занятым парам (%

факт>%

об), и нулевая гипотеза

о независимости заражения посевов от вида пара отвергается.

203

Использование критерия

при работе с таблицами состава 2x2 требует,

чтобы ни одно «з ожиданий не было меньше 5. Если теоретические численности

невелики, то, до того как вычислять

все разности (/—F) уменьшают на 0,5,

приближая их к нулю (поправка Ийтса). В нашем примере, если ввести по-

правку Ийтса, вычисления приобретают следующий вид:

5,02 (_5,0)а (—5,0)

, 5,0

Пример 5. На 260 полях ячменя учтен урожай и проведен подсчет зара-

женности почвы проволочником (Д. Д. Финки, 1957). Поля разбиты на две

группы по урожайности и на четыре группы по зараженности проволочником

(табл. 23). Зависит ли урожай ячменя от степени зараженности проволоч-

ником?

Решение. Н

: урожай не зависит от степени зараженности и колебание

соотношений удовлетворительных и неудовлетворительных урожаев в каждой

колонке таблицы является случайным.

На основе нулевой гипотезы вычисляют ожидаемые частоты для каждой

клетки таблицы. Число полей с удовлетворительным урожаем при слабой за-

раженности должно быть

умеренной

—

сильной —

и весьма сильной

—

Число полей с неудовлетворительным урожаем при слабой зараженности

22 3

/б^-Щ"-109 = 24,3,

умеренной

—

22,3

в ==

100 ~'

~ *

сильной

—

22 3

^=-щ-48 = 10,7

и весьма сильной

—<

22,3

8==

"ТОО"

2б== 5,8>

Ожидаемые числа в таблице 23 заключены в скобки.

Теоретическое значение %

о5=7,8 (по табл. 4 приложений).

Вывод. Наблюдается существенная зависимость урожаев ячменя от сте-

пени зараженности почвы проволочником (%

Факт>%

05), и нулевая гипотеза

отвергается.

Пример 6. Апробацией семенников клевера красного установлено распре-

деление ПО стеблей по числу междоузлий:

204

_^_.

109=84

77,7

"ТОО"—77

= 59,8,

77,7

= -ШГ'

77 7

.26 = 20,2.

23. Урожай ячменя в связи с заражением почвы проволочником и вычисление ожидаемой численности

полей

F по таблице 2X4

Удовлетворительный

Неудовлетворительный

Сумма

Процент

Необходимо проверить соответствие эмпирического распределения нор-

мальному по критерию %

Решение. Прежде всего по данным эмпирического распределения ча-

стот f необходимо определить теоретически ожидаемые частоты F, которые

следуют нормальному распределению, а затем установить степень соответст-

вия фактических и ожидаемых частот по критерию хи-квадрат.

Расчеты проводят в таком порядке (табл. 24):

24.

Вычисление теоретических частот (F) и критерия соответствия

эмпирического распределения нормальному (%

)

Ф(0

(f-F)

(f-Л

Сумма

1,80

1,28

0,77

0,26

0,77

1,28

1,80

2,32

ПО —

0,0790

0,1758

0,2966

0,3867

0,2966

0,1758

0,0790

0,0270

10,1

4,5

1,6

14,6

6,1

100,0

1,4

10,8

12,4

10,4

11,8

-0,1

-1,1

1,96

116,64

153,76

108,16

139,24

0,01

1,21

0,13

6,78

0,86

4,83

8,10

0,00

0,20

По формулам для сгруппированных данных определяют х и s:

- HfX

•

(6X4)+ (10X5)

К2Х12)

ПО

7,5;.

26,90=х

/"2/(*-*)

"" у п—

V-

6(4—

7,5)2+10(5

—

7,5)

-[ 1-2(12-7,5)

110 —

= 1,93.

Определяют нормированное отклонение в долях стандартного откло-

нения:

По величине t в таблице 7 приложений находят Ф(0 —вероятность

встречи данного значения признака х в нормально 'распределенной совокуп-

ности.

Рассчитывают теоретический ряд частот F, соответствующий данному

объему выборки я, х и s при величине интервала группировки i по формуле:

F = ф (0

П'1

Для нашего примера значение коэффициента

п-1 110x1

1,93

57,0.

Объединяют крайние малочисленные группы так, чтобы значение F пре-

вышало 5, рассчитывают разности

(f—F),

возводят их в-квадрат, делят на сою-

зов

Рис. 44. Эмпирическое 1 и теоретиче-

ское 2 распределение стеблей клевера

по числу междоузлий.

©тветствующие теоретические часто-

ты (f — F)

/F и полученные величи-

ны суммируют.

Сумма всех частных дает значе-

ние %

=26,90 при {к— 3) = (7—3)»4

степенях свободы вариации. Таблич-

ное значение %

=9,49 (по табл. 4

приложений).

Вывод. Распределение стеблей

красного клевера по числу междоуз-

лий существенно отличается от нор-

мального Х

факт>Х

о5 и нулевая ги-

потеза отвергается. Апробируемый

Н 5

Б 7 В 9 10

Число междоузлий

посев является, по видимому, механической смесью клеверов двух типов: ран-

неспелого (среднее число междоузлии около 6) и позднеспелого (среднее

число междоузлий около 9) (рис. 44).

§ 5. ОЦЕНКА РАЗЛИЧИЙ МЕЖДУ ДИСПЕРСИЯМИ

ПО КРИТЕРИЮ F

Существенность различий в степени вариации признаков

оценивают при помощи критерия F.

Если ^факт^/чеор, то между сравниваемыми дисперсиями

имеются существенные различия, когда /

ак

т</

еор

—

разли-

чия несущественны и нулевая гипотеза о равенстве сравнивае-

мых дисперсий не отвергается. Так как числителем всегда бе-

рется большая дисперсия, то критерий F равен единице или

больше ее. Теоретическое значение критерия F для принятого

в исследовании уровня значимости находят по таблицам 2—3

приложений с учетом числа степеней свободы сравниваемых

дисперсий.

На сравнении дисперсий построен важный статистический

метод, получивший название дисперсионного анализа, основы

которого рассмотрены ниже.

Глава 18

ДИСПЕРСИОННЫЙ АНАЛИЗ

§ 1. ОСНОВЫ МЕТОДА

Дисперсионный анализ разработан

введен в практику сель-

скохозяйственных и биологических исследований английским

ученым Р. А. Фишером, который открыл закон распределения:

отношения средних квадратов (дисперсий):

средний квадрат выборочных средних

средний квадрат объектов

207

Дисперсионный анализ широко используется для планирова-

ния эксперимента

статистической обработки его данных. Если

в недалеком прошлом считали, что роль математика состоит

лишь в анализе экспериментальных данных, то работы

Р.

А.

Фи-

шера коренным образом изменили эту точку зрения, и в на-

стоящее время статистическое планирование опыта в соответ-

ствии с требованиями дисперсионного анализа и математическая

интерпретация результатов

—

непременные условия успешного

получения ответов на вопросы, интересующие экспериментатора.

Статистически обоснованный план эксперимента определяет и

метод математического анализа результатов. Поэтому современ-

ный эксперимент нельзя правильно спланировать, не зная основ

дисперсионного анализа.

При дисперсионном анализе одновременно обрабатывают

данные нескольких выборок (вариантов), составляющих еди-

ный статистический комплекс, оформленный в виде специаль-

ной рабочей таблицы. Структура статистического комплекса и

его последующий анализ определяются схемой и методикой экс-

перимента.

Сущностью

дисперсионного анализа является расчленение

общей суммы

квадратов

отклонений и общего числа

степеней

свободы на

части —

компоненты,

соответствующие структуре

эксперимента,

и оценка

значимости действия

взаимодействия

изучаемых

факторов

по

F-критерию.

Если обрабатывают однофакторные статистические компле-

ксы, состоящие из нескольких независимых выборок, например

/-вариантов в вегетационном опыте, то общая изменчивость ре-

зультативного признака, измеряемая общей суммой квадратов

CY,

расчленяется на два компонента: варьирование между вы-

борками (вариантами) C

и внутри выборок C

. Следовательно,

в общей форме изменчивость признака может быть представле-

на выражением:

Су

= Су -f- Cz-

Здесь вариация между выборками (вариантами) представ-

ляет ту часть общей дисперсии, которая обусловлена дей-

ствием изучаемых факторов, а дисперсия внутри выборок ха-

рактеризует случайное варьирование изучаемого признака, т. е.

ошибку эксперимента.

Общее число степеней свободы (N—1) также расчленяется

на две части

—

степени свободы для вариантов (I—1) и для

случайного варьирования

(N—I):

N—1 = (/_1)-|_(#—

/).

Если обрабатывают однофакторные сопряженные статисти-

ческие комплексы, когда выборки (варианты) связаны каким-

то общим контролируемым условием, например наличием п ор-

ганизованных повторений в полевом опыте, общая сумма квад-

208

ратов разлагается на три части: варьирование повторений C

вариантов C

и случайное C

. В подобных случаях общая из-

менчивость и общее.число степеней свободы могут быть пред-

ставлены выражениями:

Cp-\-C

-{-

;

(#-1)=(л—i)+a—1)+(я—1)(2—1).

Суммы квадратов отклонений по данным полевого опыта —

статистического комплекса с /-вариантами и я-повторениями—-

находят обычно в такой последовательности. В исходной табли-

це определяют суммы по повторениям Р, вариантам

и общую*

сумму всех наблюдений

ИХ.

Затем вычисляют:

1) общее число наблюдений N

—

tn;

2) корректирующий фактор (поправку) C=(2X)

:N;

3) общую сумму квадратов

СУ

= 2Х

—С;

4) сумму квадратов для повторений

=HP

:t—С;

5) сумму квадратов для вариантов Cv=7lV

:n—С;

6) сумму квадратов для ошибки (остаток)

—C

Две последние суммы квадратов Су и C

делят на соответ-

ствующие им степени свободы, т. е. приводят к сравниваемому

виду

—

одной степени свободы вариации. В результате получа-

ют два средних квадрата (дисперсии):

вариантов

j~-

ошибки

= . _

Л»__

Эти средние квадраты и используют в дисперсионном анализе

для оценки значимости действия изучаемых факторов. Оценка

проводится путем сравнения дисперсии вариантов s

с диспер-

сией ошибки s

по критерию F

vjs

. Таким образом, за ба-

зу— единицу сравнения принимают средний квадрат случай-

ной дисперсии, которая определяет случайную ошибку экспе-

римента. При этом проверяемой нулевой гипотезой служит

предположение: все выборочные средние являются оценками

одной генеральной средней и, следовательно, различия между

ними несущественны. Если ^aKT=s

a/s

Te0

нулевая ги-

потеза Н

d—О

не отвергается; между всеми выборочными сред-

ними нет существенных различий, и на этом проверка закан-

чивается. Нулевая гипотеза отвергается, когда

-FcDaK

= s

a/s

eop.

В этом случае дополнительно оценивают существен-

ность частных различий по НСР и определяют, между какими

средними имеются значимые разности.

Теоретическое значение критерия F для принятого в иссле-

довании уровня значимости находят по таблицам 2—3 прило-

жений с учетом числа степеней свободы для дисперсии вариан-

тов и случайной дисперсии. В большинстве случаев избирают

5%-ный, а при более строгом подходе

1'%-ный

или даже

0,1%-ный уровень значимости.

При наличии общих принципов возможны разные модели,,

или конкретные схемы, дисперсионного анализа, отражающие

14—724

20»

25.

Общая схема дисперсионного анализа однофактбрнЫх

экспериментов (комплексов)

'Вид эксперимента

Сумма квадратов (в числителе) и степени

свободы (в знаменателе)

«3

Р о

й «

S а

бцо

Е-

ант

го

СО

о *

га S

О о

Вегетационные и поле-

вые опыты, проведен-

ные методом неорга-

низованных повторе-

ний (полная рендомн-

зация)

Полевые и вегетацион-

ные опыты, проведен-

ные методом органи-

зованных повторений

•Латинский квадрат

Су

N—1

Су

N—1

Су

N—1

Су

.Латинский прямоуголь-

ник

Л/

я—

СР

п—1

Ср

п—1

С с

п—1

Су

1—1

Су

N—l

I—I

(n—1)(/—1)

Cy Cz

_1 (

„i)(

_2)

Cy Cz

I—I

(n—l)(Z—2)

•условия и методику проведения эксперимента. Общая схема дис-

персионного анализа однофакторных комплексов дана в таб-

лице 25. Здесь N

—

общее число наблюдений, /

—

число вариан-

тов,

—

число повторений, рядов и столбцов. Делением суммы

•квадратов для вариантов C

и остатка C

на соответствующее

•число степеней свободы получают средние квадраты s

и s

•необходимые для расчета критерия F.

Здесь необходимо подчеркнуть, что все суммы квадратов —

•положительные числа. Отрицательное значение суммы означа-

ет, что допущена ошибка, которую следует исправить.

Из данных таблицы 25 видно, что для каждого вида экспери-

мента имеется определенная математическая модель, или схема

дисперсионного анализа. Так, урожай с единичной делянки по-

левого опыта или сосуда вегетационного опыта, проведенных

методом неорганизованных повторений, может рассматриваться

состоящим из двух компонентов: связанного с вариантом и слу-

'чайного компонента, связанного с ошибкой. В долевом опыте,

поставленном методом организованных повторений, компонен-

тов варьирования урожая будет уже три: повторение, вариант и

•ошибка; в латинском квадрате и прямоугольнике

—

четыре: ряд,

столбец, вариант и ошибка.

Ясное представление о математической модели дисперсион-

ного анализа облегчает понимание необходимых вычислитель-

но

ных операций, особенно при обработке данных многофакторных

опытов,

в которых больше источников варьирования, чем в про-

стых, однофакторных опытах. Например, в двухфакторном опы-

те,

поставленном методом обычных повторений, сумма квадра-

тов для вариантов C

расчленяется на три, а в трехфактор-

ном

—

на семь компонентов. Общая сумма квадратов для этих,

опытов будет представлена следующими выражениями (в скоб-

ках указаны суммы квадратов для изучаемых факторов Л, В, С

и их взаимодействия):

= (С

-j-

АВ

)

-J-

-f- C

Су

= (С

+С

-{-

АС

-j-

-{-

АВС

)

-\-C

Соответственно указанным компонентам варьирования ре-

зультативного признака разлагают и общее число степеней сво-

боды.

Часто многофакторные опыты закладывают по методу слож-

ных, или расщепленных, делянок. В этом случае не все сравне-

ния можно провести с одинаковой степенью точности. Неравно-

точность различных сравнений, вытекающая из расположения

вариантов на расщепленной делянке, требует расслоения ошиб-

ки опыта в соответствии с составляющими ее компонентами: на

ошибку для вариантов, размещенных на делянках первого по-

рядка

CZL

на ошибку для делянок второго порядка C

n и т. д.

Эти ошибки и используют затем для оценки действия и взаимо-

действия факторов. Например, для двух- и трехфакторных поле-

вых опытов, проведенных соответственно с двойным и тройными

расщеплением делянок, общая сумма квадратов будет равна:

-\-C

)-\"Cp-\-C

i-\-C

ii;

Су

—

(СА+С

в+Сс +

CAB+С

АС

~Ь С

вс

-f-

ABC

)

-J-

+С

-j-

\+C

-j-

Таким образом, в опытах с расщепленными делянками оцен-

ка существенности различий будет опираться не на одну оста.-

точную сумму квадратов C

, как это было во всех предшест-

вующих примерах, а на суммы квадратов, рассчитанные для де-

лянок первого, второго и третьего порядков.

Для упрощения расчетов сумм квадратов, особенно при от-

сутствии вычислительной машины, исходные даты обычно пре-

образуют (кодируют) путем вычитания из результатов измере-

ний условного начала А —одного

joro же целого числа, близ-

кого к среднему урожаю по опыту х. Изменение начала отсчета.

не оказывает влияния на суммы квадратов и позволяет рабо-

тать с малозначными цифрами.

Дисперсионный анализ дает возможность получить представ-

ление о степени, или доле влияния того или иного фактора в

Н*

211.

юбщей дисперсии признака, которую принимают за единицу

.или 100%, а именно:

= -=^—влияние вариантов;

Су

г]

= _£—влияние повторений;

ц^ = —£—влияние случайных факторов;

Г[

Т1

-j-

т]р

-{-

= 1,0 (или 100 %)—влияние всех факторов.

Отношение сумм квадратов вариантов, повторений и остат-

ка к общему варьированию, обозначенное здесь соответственно

у, tfp, rf

, показывает долю участия отдельных факторов в

общей изменчивости признака. При этом

= ]Ai„

Y~CJC

корреляционное отношение, характеризующее тесноту связи ре-

зультативного признака с факториальным, a rfv

—

индекс де-

терминации, показывающий долю его варьирования под воздей-

ствием изучаемых факторов.

Дисперсионный анализ быстро вошел в употребление при

-обработке экспериментальных данных благодаря следующим ос-

новным преимуществам его перед методом попарных сравнений

по критерию Стьюдента:

1) вместо индивидуальных ошибок, средних по каждому ва-

рианту, в дисперсионном анализе используется обобщенная

-ошибка .средних, которая опирается на большее число наблюде-

ний и, следовательно, является более надежной базой для оце-

нок;

2) методом дисперсионного анализа можно обрабатывать

данные простых и сложных, однолетних и многолетних, одно-

•факторных и многофакторных опытов;

3) дисперсионный анализ позволяет избежать громоздких

вычислений при большом числе вариантов в опыте и позволяет

компактно в виде существенных разностей представить итоги

статистической обработки.

Современная теория планирования эксперимента и статисти-.

ческий анализ 'базируются на принципах рендомизации. Теория

требует, чтобы все наблюдения были независимы. В этом слу-

чае дисперсионный анализ дает правильную, несмещенную

-оценку ошибки эксперимента. Следовательно, если опыт не рен-

домизирован, то экспериментатор может получить смещенную

оценку ошибки опыта, и обычно используемые в дисперсионном

анализе критерии значимости теряют законную силу и не могут

использоваться в качестве аргументов строго статистического

доказательства эффектов вариантов.

Дисперсионный анализ невозможен для простых вегетаци-

онных или полевых опытов, проведенных без повторностей. Ми-

нимум повторностей

—

две, однако в этом случае, особенно в

полевых опытах, получаются большие ошибки и статистически

212