Доспехов Б.А. Методика полевого опыта

Подождите немного. Документ загружается.

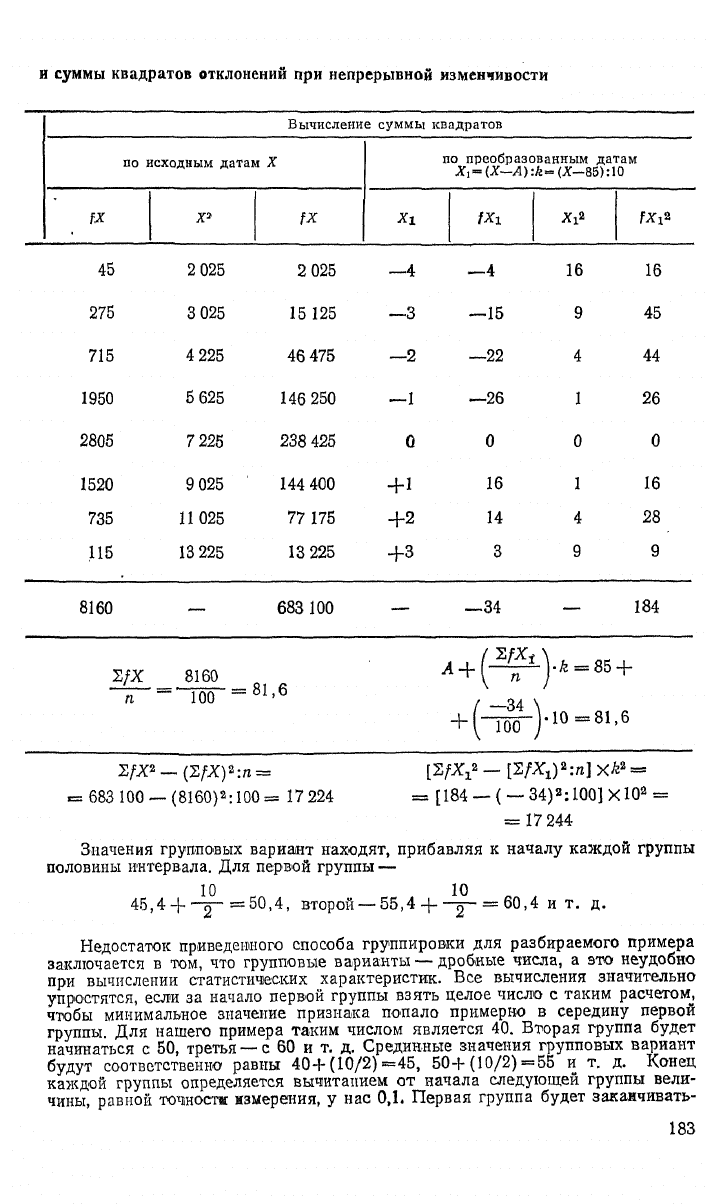
и суммы квадратов отклонений при непрерывной изменчивости

Вычисление суммы квадратов

по исходным датам X

X» fX

по преобразованным датам

^1=(Х-Л):/г«=(Х-85):10

fXi

Хх*

№

275

715

1950

2805

1520

735

,115

2 025

3 025

4 225

5 625

7 225

9 025

11025

225

2 025

15 125

46 475

146 250

238 425

144 400

77 175

13 225

—4

—3

—2

—1

—15

—22

—26

8160

683 100

—34

184

2/Х

8160

100

81,6

+ (-w-)-

2Д

— (2Д)2:/г =

683100 —(8160)2.-100= 17224

==1

184 — (

—34)2;

100]

ХЮ

244

Значения групповых вариант находят, прибавляя к началу каждой группы

половины интервала. Для первой группы

—

10 10

46,4 + ""f =50,4, второй —55,4 +

—2~

= 60,4 и т. д.

Недостаток приведенного способа группировки для разбираемого примера

заключается в том, что групповые варианты —дробные числа, а это неудобно

при вычислении статистических характеристик. Все вычисления значительно

упростятся, если за начало первой группы взять целое число с таким расчетом,

чтобы минимальное значение признака попало примерно в середину первой

группы. Для нашего примера таким числом является 40. Вторая группа будет

начинаться с 50, третья —с 60 и т. д. Срединные значения групповых вариант

будут соответственно равны 40+(10/2) =45, 50+ (10/2) =55 и т. д. Конец

каждой группы определяется вычитанием от начала следующей группы вели-

чины, равной ТОЧНОСТИ измерения, у нас

0,1.

Первая группа будет закаичивать-

183

ся числом 50,0—0,1=49,9; вторая 60,0—0,1=59,9 и т. д. В итоге получаются

следующие 8 групп:

40,0—49,9 80,0—89,9

50,0—59,9 90,0—99,9

60,0—69,9 100,0—109,9

70,0—79,9 110,0—120,0

Составить "рабочую таблицу и разнести исходные данные по группам,

используя способ «штрихов» или «конвертиков» (табл. 12).

Правильность разноски проверяют повторным составлением аналогичной

таблицы.

После группировки получается короткий, легко обозримый вариационный

ряд, позволяющий судить о характере изменчивости изучаемого признака. Так,

наиболее часто встречаются растения с технической длиной стебля 80,0—

89,9 см. Группа, обладающая наибольшей частотой, получила название мо-

дальной (мода — наиболее часто встречающийся), значения крайних групп на-

зываются лимитами или пределами.

Определить среднее арифметическое и сумму квадратов отклонений.

В таблице 13 показано два способа вычисления этих величин: первый ис-

пользуется при наличии вычислительной машины; второй —при ее отсутствии,

Определить статистические характеристики вариационного ряда и дове-

рительный интервал для генеральной средней.

Вычисления рекомендуется вести в такой последовательности:

а) средняя арифметическая (взвешенная)

- 2/Х

б) дисперсия

81,6 см;

2/(Х

—

х)

17 244

о2 '-Л '- 174 9 •

—

_1 — 99 ~

1/4

в) стандартное отклонение (ошибка отдельного наблюдения)

s = У&= УШ~2 = 13,2 см;

г) коэффициент вариации

s 13,2

0 = —-100=

-100 = 16,2%;

д) абсолютная ошибка выборочной средней

s 13,2

S_ = .— = гт:— =1,32 СМ;

х Уп

е) относительная ошибка выборочной средней

S- 1 32

e-%=~-100= -gj-g-100= 1,6% (отн.);

ж) доверительный интервал генеральной средней для 5%-ного уровня зна-

чимости при

п—1

= 100—1=99 степенях свободы вариации (^5=1,98)

*±*ов«-=81.6± 1,98 х 1,32= 81,6±2,6(79,Он-84,2).

Таким образом, средняя всей совокупности с 95% -ным уровнем вероятно-

сти находится в интервале 79,0ч-84,2 см, абсолютная ошибка выборочной сред-

ней— 1,32 см, относительная— 1,6%; коэффициент вариации технической дли-

ны льна— 16,2%.

184

Рис.

43. Графическое изображение

распределения 100 растений льна по

технической длине стеблей (гисто-

грамма и полигон).

Построить гистограмму и по-

лигон распределения " 100 растений

льна по технической длине стебля

(рис.

43).

По горизонтальной оси абсцисс

наносят значения границ групп, а по

оси ординат частоту f. В итоге полу-

чают ступенчатый график в виде

столбиков, имеющих высоту, пропор-

циональную частотам, а ширину, рав-

ную интервалу L Такой график назы-

вается гистограммой. Соединив лини-

ями срединные значения групп, полу-

чим полигон — кривую распределения.

Желательно, чтобы соотношение ши-

рины и высоты графика было близко

к 1: 2.

Глава 16

ВЫЧИСЛЕНИЕ СТАТИСТИЧЕСКИХ ХАРАКТЕРИСТИК

ВЫБОРКИ ПРИ ИЗУЧЕНИИ КАЧЕСТВЕННЫХ ПРИЗНАКОВ

К качественным относят такие признаки, которые выража-

ются в каких-то качествах, не поддающихся количественному

измерению,

—

разные сельскохозяйственные культуры, разные

виды болезней, окраска зерна или цветков, форма плода, на-

личие или отсутствие признаков или реакции на воздействие

и т. д. Наиболее часто при изучении качественных признаков

встречается случай, когда изучаемая совокупность представле-

на объектами только с двумя градациями

—

признак есть и при-

знака нет, т. е. имеется две возможности, две альтернативы.

Такое распределение называется альтернативным (двояковоз-

можным).

Сводные статистические характеристики вычисляют по фор-

мулам таблицы 14. В таблице ръ

р%,...,рк

и q обозначают доли

признака в совокупности: п\, «2, ••,

л*

—

численность группы;

/V —

объем выборки; k

—

число градаций признака; t — теоре-

тическое значение критерия Стыодента.

Вычисления сводных характеристик выборки при качествен-

ной изменчивости складываются из распределения исходных

наблюдений по группам (классам), определения среднего зна-

чения доли, изменчивости признака и доверительного интерва-

ла, в пределах которого находится значение доли в генеральной

совокупности. При вычислении коэффициента вариации следу-

ет иметь в виду, что максимально возможная изменчивость

акс

при двух градациях признаков равна 0,500 (50,0%'), трех

—

0,333 (33,3%), четырех —0,250 (25,0%); пяти —0,200 (20,0%)

и шести —0,167 (16,7%).

-j |— ^ ^ ^_р* ^

sip».

ЦО 55,2 68,4

81,6

f,8

108,0 121,2

-3S -2S S х +$ +2S +2S

Интервал группировки

съ

СЭ

еп

е=»

'Off

СП

Сэ

см

70,

<*i

en;

СЭ

»*

<*>

Й?"

120

185

14.

Формулы для вычисления статистических характеристик

выборки при качественной изменчивости

Показатель

Формула

Доля признака

при k=2

при k>2

—

Рг

Р%

\~р

• Pk-~jr

Стандартное отклонение

при k=2

при А>2

lg*

s=Ypq; s = yp

X--Pk

lg p

+ lg p

-1

lg p

Коэффициент вариации

Ошибка доли

Доверительный интервал

для доли признака в

совокупности

- -100

макс

i /~Pf

"VN ~ у N

p d= ls

Степень свободы N — 1

Пример 1. При просмотре 500 растений льна было обнаружено 50 расте-

ний, пораженных фузариозом. Определить 95%-ные и 99%-ные доверительные

интервалы для генеральной доли пораженных растений в совокупности.

Решение. Исходные данные при альтернативной (двояковозможной)

изменчивости распределяют по двум группам. Первая группа — растения, име-

ющие признак, в нашем примере — пораженные растения

(ni

50),

и вторая

группа — растения, у которых этот признак отсутствует, т. е. здоровые расте-

ния {n

=N—ni = 500—50=450).

Вычисления сводных характеристик выборки ведут в такой последователь-

ности:

а) доля пораженных (р) и здоровых (q) растений

я,

= -&- =-Еп7Г=0,10 (или 10%);

500

q= 1 —р =

1_о,10

= 0,90 (или 90%);

б) стандартное отклонение доли

s= Vpq = /0,10-0,90 =0,30 (или 30%);

в) коэффициент вариации (при k=2; 5

маК

с=0,50)

1ПЛ

0,30

%акс

100= -^5Т

100==60

г) ошибка выборочной доли

лГ

РЯ

т/0,10-0,90

У -лГ= V —500 = °>013 (или

1,3%);

186

д) доверительный 95%-ный интервал генеральной доли пораженных фу-

зариозом растений в совокупности

(^ОБ=

1,96 при

N—1

500—1

= 499)

P±/

6Sp = 0,10d=

1,96-0,013

= 0,10^0,025(0,075-^0,125 или 7,5 4-12,5%).

Таким образом, генеральная доля растений, пораженных фузариозом в

изучаемой совокупности с 95%-пым уровнем вероятности, составляет 7,5—

12,5%,

ошибка репрезентативности s

=l,3%, коэффициент вариации 60,0%.

Пример 2. После распределения зерен озимой пшеницы по стекловидности

получены данные (штук, зерен): полностью стекловидные

/Zi

658;

частично

стекловидные «2=102; мучнистые /г

=60.

Определить процентное содержание каждой группы зерен в выборке и их

доверительные интервалы в генеральной совокупности с

1%-ным

уровнем зна-

чимости.

Решение. Объем выборки Ы=щ + п

+я

=658 +102-1-60=820.

Статистические характеристики:

а) доля зерен в совокупности

полностью стекловидных

щ 658

/Ji==

_l_

-_-_

0,80 (или 80%);

частично стекловидных

По

102

= ~ir = "820" = °'

или

12%

^ •'

мучнистых

"F"

(

илн 8

/о

;

б) стандартное отклонение доли

lgPi + lgP

+ lgp

Ig0,80+lg0,12 + lg0,08

lgs==

_ =,

Г,9031+Г, 0792 +

2", 9031

3",8854

Гоок

s = antilgf,2951 = 0,1979 « 0,198 (или 19,8%);

в) коэффициент вариации (при

/г

=0,333)

0,198

= 100 =

ЮО

59,5%

;

макс

°°°

г) ошибка доли

s 0 198

= —^ = ,'— = 0,0069 ^ 0,007 (или 0,7%);

у N У 820

д) доверительные интервалы для

1%-иого

уровня значимости (/

i=2,58

при

iV—1

820—1

= 819);

для полностью стекловидных зерен

1±

= 0,80±:2,58-0,007 =

= 0,80 ±0,018 (0,782-г 0,818 или 78,2-^81,8%);

для частично стекловидных зерен

±/

1*р = 0,12±2,58.0,007 =

= 0,12 ±0,018^(0,102 4-0,138 или 10,2ч- 13,8%);

187

для мучнистых зерен

±*oiSp = 0,08 ±2,58-0,007 =

= 0,08±0,018 (0,062—0,098 или 6,2—9,8%).

Результаты выборочного наблюдения позволяют считать, что генеральная

доля полностью стекловидных зерен в совокупности находится в интервале

78,2-5-81,8%,

частично стекловидных

— в

интервале 10,2-*-13,8% и мучнистых

—

в интервале от 6,2 до 9,8%. Уровень значимости данного заключения состав-

ляет 1%.

Глава 17

СТАТИСТИЧЕСКИЕ МЕТОДЫ ПРОВЕРКИ ГИПОТЕЗ

Вопрос о статистической проверке гипотез

—

один из основ-

ных при применении математической статистики в научных ис-

следованиях. Статистические методы или критерии проверки

гипотез — надежная основа принятия тех или иных решений

при некоторой неопределенности, обусловленной случайной ва-

риацией изучаемых явлений. Они применяются всегда, когда

необходимо использовать выборочное наблюдение для- сужде-

ния о законе распределения совокупности, для решения вопро-

са о существенности разности между выборочными средними,

для установления принадлежности варианты к данной совокуп-

ности и соответствия между фактическими и теоретическими

распределениями частот.

Практически проверка гипотез часто сводится к сравнению

статистических характеристик, оценивающих параметры законов

распределения, т. е. к проверке определенных статистических

гипотез. Вообще статистической гипотезой называют

научное предположение о тех или иных статистических законах

распределения рассматриваемых случайных величин, которое

может быть проверено на основе выборки. В большинстве слу-

чаев задача сводится к проверке гипотезы об отсутствии реаль-

ного различия между фактическими и теоретически ожидае-

мыми наблюдениями. Эту гипотезу называют нулевой ги-

потезой и обозначают символом Я

Если в результате проверки Я

различия между фактиче-

скими и гипотетическими показателями близки к нулю или на-

ходятся в области допустимых значений, то нулевая гипотеза

не опровергается, а если различия оказываются в критической

для данного статистического критерия области, которые при

нашей гипотезе невозможны, а потому несовместимы с ней,

опровергается. Принятие нулевой гипотезы означает, что

данные наблюдений не противоречат предположению об отсутст-

вии различий между фактическими и гипотетическими (теорети-

ческими) или между двумя рядами фактических распределе-

ний, но не доказывают отсутствия такого различия. Отбрасыва-

ние гипотезы означает, что эмпирические данные несовместимы

Но,

а верна другая, альтернативная гипотеза.

188

Справедливость нулевой гипотезы проверяется вычислением

статистических критериев проверки для определенного уровня

значимости.

Уровень значимости определяется конкретными задачами

исследования; он характеризует, в какой мере мы рискуем оши-

биться, отвергая нулевую гипотезу. Чем меньше уровень значи-

мости, тем меньше вероятность отвергнуть H

, когда она вер-

на, или, как говорят, совершить ошибку I рода, но тем больше

вероятность совершить ошибку II рода, когда не отвергают Но,

в действительности неверную. Уровень значимости не измеряет

степень риска, связанный с принятием неверной гипотезы

(ошибка II рода), он контролирует лишь ошибку I рода.

Для проверки статистической гипотезы Я

используют кри-

терии двух видов: параметрические и непарамет-

рические.

Параметрическими называют критерии, которые осно-

ваны на предположении, что распределение признака в сово-

купности подчиняется некоторому известному закону, например

закону нормального распределения. К таким критериям отно-

сятся, -в частности, критерии t и F, применение которых требу-

ет вычисления оценок параметров распределения.

Непараметрическими называют критерии, использо-

вание которых не требует предварительного вычисления оценок

неизвестных параметров распределения и даже приближенного-

значения закона распределения признака. Они могут применять-

ся и тогда, когда распределение сильно отклоняется от нор-

мального. С другой стороны, непараметрические критерии ме-

нее эффективны по сравнению с параметрическими, и поэтому

их целесообразно использовать только в предварительных ис-

следованиях.

§ 1. ТОЧЕЧНАЯ И ИНТЕРВАЛЬНЫЕ ОЦЕНКИ

ПАРАМЕТРОВ РАСПРЕДЕЛЕНИЯ

Статистические характеристики выборочной совокупности

являются приближенными оценками неизвестных параметров

генеральной совокупности. Оценка может быть представлена

одним числом, точкой (точечная оценка) или некоторым

интервалом (интервальная оценка), в котором с опре-

деленной вероятностью может находиться искомый параметр.

Так, выборочная средняя х является несмещенной и наиболее

эффективной точечной оценкой генеральной средней \i, а выбо-

рочная дисперсия

—

несмещенной точечной оценкой генераль-

ной дисперсии а

. Обозначая ошибку выборочной средней s*,

точечную оценку генеральное средней можно записать в- виде-

#±s.x.

Это"

означает, что х оценка генеральной средней

\х с

ошиб-

кой, равной 5,".

Естественно, что точечные статистические оценки х us

не

.должны иметь систематической ошибки в сторону завышения

или занижения оцениваемых параметров

JLI

И а

. Оценки, удов-

летворяющие такому условию, называют несмещенными.

Интервальной называют оценку, которая характеризуется

двумя числами

—

концами интервала, покрывающего оценивае-

мый параметр. Доверительным называют такой интер-

вал, который с заданной вероятностью покрывает оцениваемый

параметр. Центр такого интервала

—

выборочная оценка точ-

ки,

а пределы, или доверительные границы, интервала опреде-

ляются средней ошибкой оценки и уровнем вероятности. Таким

образом, интервальная оценка является дальнейшим развити-

ем точечной оценки, которая при малом объеме выборки неэф-

фективна.

В общем виде доверительный интервал для генеральной,

средней записывается так:

1с—

is-

м-

+ %•.

или в более компактной форме:

x±.ts~.

Здесь

tSx —

предельная ошибка выборочной средней при данном

числе степеней свободы и принятом уровне значимости.'Зна-

чение критерия Стыодента для различных уровней значимости

и числа степеней свободы можно взять из таблицы 1 приложе-

ний.

Пример 1. При определении содержания белка в зерне пшеницы найдены

следующие значения: ж=

14,80%,

sj =0,20'%, n=4. Определить 95%-ный и

'99%-нын доверительные интервалы для генеральной средней. По таблице 1

.приложений для 4—1=3 степеней свободы ^5=3,18 и

*oi

= 5,84, т. е. ширина

•95%-нопо доверительного интервала составляет 3,18 sj и 99%-того интерва-

ла

—

5,84 S.7-. Найдем доверительные интервалы:

95%—

x±t

s-= 14,80 ±3,18-0,20 =

= 14,80± 0,64 (14,16 — 15,44);

99%-x±*oiS-

= 14,80± 5,84-0,20 =

=14,80± 1,17 (13,63 ~ 15,97).

Такая запись говорит о том, что с вероятностью 95% генеральная сред-

няя содержания белка в зерне пшеницы заключена в интервале от 14,16 до

15,44%

и с вероятностью 99%—от 13,63 до 15,97%. Вероятность выйти за

эти интервалы, т. е. вероятность попасть в критическую область, в первом слу-

чае составляет 5% и во втором— 1% (уровень значимости).

Крайние точки интервала

—

начало х—is? и конец x-\-ts-x—

называются доверительными границами.

Интервальную оценку параметров распределения можно ис-

пользовать для статистической проверки гипотез при сравнении

выборочных средних.

190

Пусть, например, при л=10 были получены такие выборочные средние w

ошибки средних:

bs- =22,0±0,5 и £±s_ = 20,4± 0,8.

Необходимо определить, существенно ли различаются эти выборочные-

средние при 0,95—95%-ном уровне вероятности, или 0,05—5%-ном уровне зна-

чимости, т. е. проверить нулевую гипотезу Н

: \х,\—|i

=<i=0. Для

10-—1

= 9

степеней свободы /

=2,26 и 95%-ные доверительные интервалы равны:

*i±*

=22,0±2,26-0,5 = 22,0± 1,1 (20,9 4-23,1);

±t

=20,4± 2,26-0,8 = 20,4 ±

1,8(18,6

4-22,2).

х%

Доверительные интервалы для генеральных средних перекрывают друг

друга, и, следовательно, разность между выборочными средними d=x\—ж

= 1,6 нельзя переносить на генеральные средние щ и [Л

, так как генеральная-

разность между ними D—\i{—[Л

может быть равна и нулю и даже отрица-

тельной величине, когда

M-

>[XI.

Поэтому Я

: d=0 не отвергается.

Нулевую гипотезу об отсутствии существенных различий между выбо-

рочными средними можно проверить и другим способом интервальной оценки-

генеральных параметров совокупности. По формуле

можно определить ошибку разности средних, а затем описанным выше спо-

собом рассчитать доверительные интервалы для генеральной разности сред-

них D. Если доверительные интервалы перекрывают нулевое значение и вклю-

чают область отрицательных величин, то Hold

—0

не отвергается, а если ле-

жат в области положительных величии, то #о отвергается и разность признает-

ся существенной. Для примера 1 разность d—x\—х

=22,0—20,4=1,6; ошибка

1/4+4

-/°

>5а

+°-

= °-

При П\-\-П2—2=10+10—2=18 степенях свободы /

5=2,10 и

(

= 2,88.

Найдем доверительные интервалы для генеральной разности:

95o/

-_d

l,6±2,l-0

9= 1,6 ±1,9 (—0,3 ч-3,5);

99Q/o—d±/

=l,6±2,88-0,9 = l,6±2,6(—1,0

—

4,2).

Нулевая гипотеза H

:d=0 не отвергается, так как доверительные интер-

валы включают нуль и область отрицательных величии, т, е. разность меньше

предельной случайной ошибки разности (d<tsd).

Величина, указывающая границу предельным случайным

отклонениям, называется наименьшей существенной

разностью. Ее -сокращенно обозначают НСР и определяют

по соотношению:

HCP

= fc

Если фактическая разность между выборочными средними

d^sHCP, то #о отвергается, а если d<HCP

—

не отвергается.

Наименьшая существенная разность широко используется

при построении доверительных интервалов и проверке статисти-

ческих гипотез. Доверительный интервал для разности гене-

ральных средних определяется по соотношению:

d—HCP<D<d-fHCP или d±HCP.

191

15.

Формулы средних ошибок выборочных оценок

Вид выборочной оценки

Средняя ошибка выборочной оценки

•Средняя выборочная х

Доля признака р

Стандартное отклонение s

Коэффициент вариации V

Разность между выборочными сред-

ними d=X± Х2

Разность между выборочными доля-

ми d

=pi—p2

Коэффициент линейной корреляции

при малых г

Vn У п

•j/2/г

Y~2h

= 1/

£-

V xi ' j

P1 "Г

-~ Г n—1

Коэффициент

Ъух

линейной регрессии

2(у —

у)'-

2(х—

х)

Здесь

HCP*

= fe

— предельная ошибка разности выборочных

•средних при данном числе степеней свободы

= «i+rt

—2 и

принятом уровне значимости.

По величине стандартного отклонения sоценивается интер-

вал для отдельного значения X и всей сово-

купно сти:

х—йз<

|Л<

x-\-ts,

или в более компактном виде xdzits. Внутри этого интервала с

95%-ным или 99%-ным уровнем вероятности будут находиться

значение генеральной средней \л и все индивидуальные значения

варьирующей величины.

Для примера 1 при s=0,40 доверительные интервалы для от-

дельных значений и всей совокупности равны:

95%—xrt zf

s= 14,80 ±3,18-0,40 =

= 14,80 ± 1,27 (13,53 ~ 16,07);

99%—

xztit

s= 14,80 ± 5,84-0,40 =

= 14,80 ±2,34 (12,46-+-17,14).

* Наименьшая существенная разность в английской и американской науч-

ной литературе обозначается LSD (начальные буквы анг. Least significant

•difference), а в немецкой — GD (начальные буквы нем. Gesicherte Differenz).

192