Доронин С.В. Проектные расчеты конструкций металлургического оборудования

Подождите немного. Документ загружается.

Предельная (относи-

тельная разрушающая)

нагрузка круговой арки

0пр0

MRPP 

Предельные нагрузки пластин. Пластины являются одним из

наиболее часто встречающихся элементов конструкций. Весьма разнооб-

разны как формы используемых пластин, так и условия их нагружения,

поэтому в практике расчетной и исследовательской работы задачи по

определению несущей способности пластин занимают значительное ме-

сто. Наиболее разработанными и широко используемыми являются ре-

шения для круглых и кольцевых пластин при осесимметричном нагруже-

нии поперечными силами, в том числе при наличии жесткого ядра, ореб-

ренных круглых и некруглых пластин (табл. 4). Основной локальной ха-

рактеристикой прочности пластин является предельный изгибающий мо-

мент на единицу длины контура M

= 

/4, где h – толщина пластины.

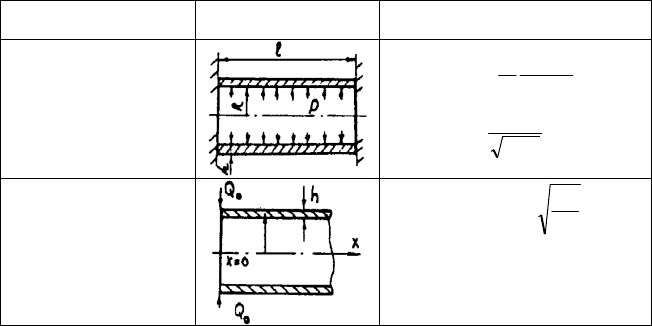
Таблица 4. Расчетные схемы и предельные нагрузки пластин

Наименование Расчетная схема Формула

Предельная попереч-

ная нагрузка круглой

осесимметричной

пластины

M2Q

0пр





Верхняя и нижняя

оценки предельного

момента, действую-

щего через жесткое

ядро на кольцевую

пластину







62,4

ив

;







46,4

ив

;

ba ;

при  < 0,077 M

ин

= 4,14

Предельная распреде-

ленная нагрузка ореб-

ренной круглой пла-

стины

 

;







Предельная сосредо-

точенная центральная

нагрузка прямоуголь-

ной пластины

M4Q

0пр





Отличительной чертой решений для большинства пластин, за ис-

ключением оребренных, является то, что суммарная предельная попереч-

ная нагрузка на пластину не зависит от ее абсолютных размеров в плане.

Она определяется локальной прочностью M

, относительными парамет-

рами, характеризующими геометрию пластины (например, относитель-

ный радиус отверстия или приложения сосредоточенной нагрузки) и ус-

ловиями закрепления.

Несущая способность оболочек. Оболочечные конструкции

представляют наибольшую трудность для исследования, поэтому анали-

тических решений для них получено относительно немного, причем ис-

следования проводились почти исключительно для осесимметричных

оболочек под действием осесимметричной нагрузки. Наибольшее коли-

чество решений получено для цилиндрических оболочек (табл. 5). При-

няты следующие основные обозначения: R – средний радиус оболочки; h

– толщина оболочки.

Таблица 5. Расчетные схемы и предельные нагрузки оболочек

Наименование Расчетная схема Формула

Предельное внутрен-

не давление защем-

ленной по краям ци-

линдрической обо-

лочки

Rh2

;

тпр







Предельная перере-

зывающая сила на-

груженной по краю

цилиндрической обо-

лочки

тпр



Предельные нагрузки массивных тел. Некоторые классиче-

ские плоские и трехмерные задачи теории пластичности могут рассмат-

риваться как задачи по определению несущей способности массивных

тел. Известные задачи нагружения кольцевого диска и полой сферы

внутренним давлением (табл. 6), вращения диска постоянной толщины,

вдавливания штампов в полуплоскость и полупространство, решенные

для жесткопластического материала, представляют собой фактически

типичные задачи предельного равновесия, так как, построенные метода-

ми теории пластичности поля напряжений и скоростей перемещений,

обычно удовлетворяют условиям, накладываемым теорией предельного

равновесия на статически и кинематически допустимые поля.

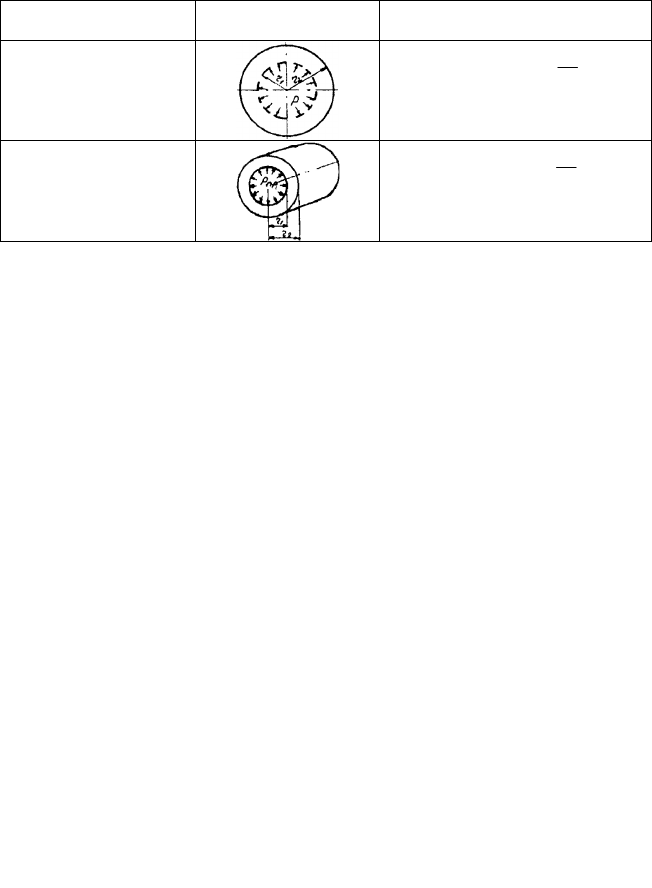
Таблица 6. Расчетные схемы и предельные нагрузки массивных тел

Наименование Расчетная схема Формула

Предельное внутрен-

нее давление толсто-

стенного сферическо-

го сосуда

тпр

ln2P 

Предельное внутрен-

нее давление толсто-

стенной трубы

тпр

ln2P 

Рассмотренные расчетные схемы (табл. 3–6) представляют собой

незначительную часть полученных за последние десятилетия и опубли-

кованных в литературе результатов. Важнейшей задачей, решаемой при

проектных расчетах, является анализ внешних нагрузок, оценка условий

работы и характера испытываемых элементом конструкции деформаций.

Это дает возможность выбрать расчетную схему, наиболее адекватно

описывающую особенности проектируемого объекта.

Большинство расчетных схем построены с учетом только сило-

вых факторов. Однако учет температурных воздействий, необходимый

для многих типов металлургического оборудования, приводит к приме-

нению специфических методов и приемов проектных расчетов.

3.2. ОСОБЕННОСТИ РАСЧЕТА НА ТЕПЛОВЫЕ

ВОЗДЕЙСТВИЯ

В конструкциях, циклически изменяющих во времени свое тем-

пературное поле, возникает поле термических напряжений, также цикли-

чески изменяющееся во времени. До тех пор пока термические напряже-

ния вызывают только упругие деформации, конструкция может работать

сколь угодно долго без нарушения несущей способности. Если же цикли-

ческие тепловоздействия вызывают упруго-пластические деформации, то

возникает одно из следующих явлений [10]:

пластические деформации неограниченно возрастают с течением

времени – тело разрушается в течение первого цикла;

пластические деформации, оставаясь ограниченными по

величине, циклически изменяются в некоторых пределах – тело разруша-

ется от усталости;

с течением времени в теле развивается некоторое поле остаточ-

ных напряжений, исключающее возможность пластического течения при

всех дальнейших изменениях внешних сил – система приспособляется.

Вопрос о том, разрушится тело от усталости или приспособится

к заданным циклам нагрузки, обычно решается на основе теоремы Мела-

на, сущность которой заключается в следующем. Если можно найти та-

кое, не зависящее от времени, распределение остаточных напряжений,

при котором их сумма с условными упругими напряжениями в каждой

точке тела образует напряженное состояние, находящееся внутри по-

верхности текучести при всевозможных комбинациях нагрузок (лежащих

в заданных пределах}, то конструкция приспособится к данной програм-

ме циклического нагружения. При этом условными упругими считаются

напряжения, подсчитанные в предположении совершенной упругости

материала независимо от уровня температуры и напряжений.

Вопрос о приспособляемости конструкций, работающих в усло-

виях циклических термоупруго-пластических деформаций, решался ря-

дом авторов (на основе теоремы Мелана). Важным результатом этих ра-

бот является то обстоятельство, что полученные выводы позволяют ре-

шать задачи теории приспособляемости при циклических тепловых на-

грузках, оперируя анализом условных термоупругих напряжений.

Если в процессе решения задачи установлено, что данное тело не

сможет приспособиться к заданной программе циклического теплового

нагружения, то возникает вопрос: через сколько циклов тело разрушится

от усталости. Появляется необходимость решать задачу о долговечности

конструкции. В основе ее решения лежит экспериментальная формула Л.

Ф. Коффина, связывающая величину пластической деформации с коли-

чеством циклов до разрушения:

 , (19)

где N – количество циклов «нагрев–охлаждение» до разрушения; 

–

пластическая деформация за цикл; m и С – постоянные для данного мате-

риала величины. Постоянная m для большинства конструкционных мате-

риалов может быть принята равной 0,5. Что же касается величины С, то

ее можно определять, помимо экспериментального метода, следующим

образом.

1. Используя энергетические представления о разрушении

металлов при механической усталости. В этом случае

4,1C

пл



 ,

где L

пл

– скрытая теплота плавления материала, дж/кг;  – плотность ма-

териала, кг/м

; G – модуль сдвига, Н/м

2. Используя то обстоятельство, что константа С практически

равна половине деформации при кратковременном разрыве.

Основным затруднением при решении задач о долговечности

конструкции с помощью формулы (19) является сложность аналитиче-

ского определения величины пластической деформации 

. В настоящее

время используются деформационная теория Ильюшина и различные

теории течения, из которых наиболее простой и употребительной оказа-

лась теория течения Прандтля-Рейсса. Деформационная теория пластич-

ности является по существу теорией нелинейной упругости и поэтому

может быть применима лишь для случая простого (или близкого к про-

стому) нагружения при активной деформации. Применять деформаци-

онную теорию пластичности к решению задач термоупруго-пластичности

при циклическом нагреве тела можно, предварительно доказав, что путь

нагружения будет близким к простому. Теория течения в математическом

отношении значительно сложнее деформационной теории, однако она

более реально описывает процесс упруго-пластического деформирования

тела.

Теоретические и экспериментальные исследования температур-

ных напряжений в элементах конструкций и деталях металлургического

оборудования достаточно многочисленны [10–12], причем необходимо

отметить определяющее влияние на распределение температур и полей

напряжений двух факторов – начальных условий (источника нагрева) и

конструктивной формы. Что касается последнего фактора, то необходимо

отметить что именно особенности формы исследуемого объекта влияют

не только на распределения температур и напряжений, но и на выбор ме-

тода анализа.

Рассмотрим в качестве примера задачу моделирования полей

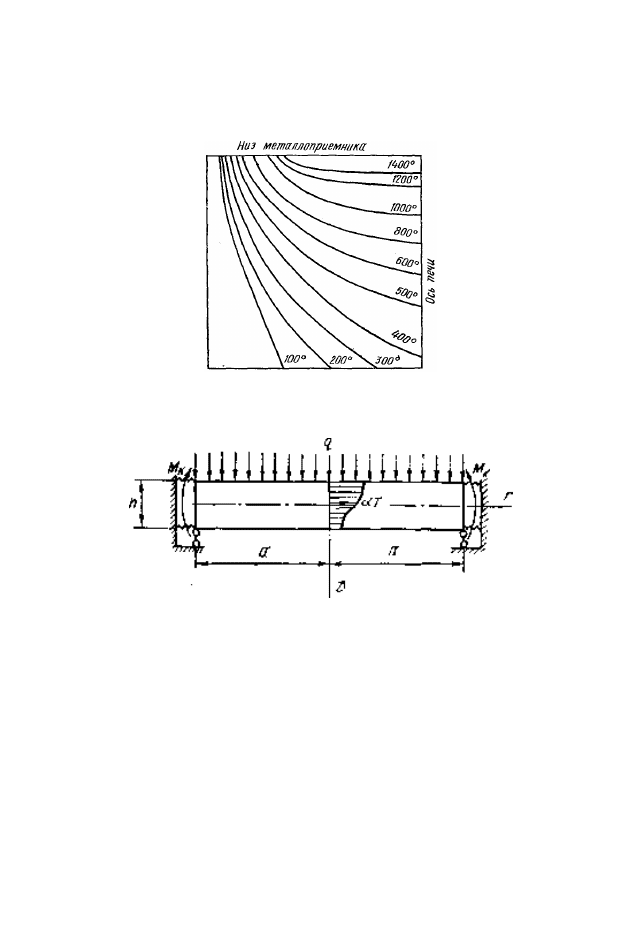
температур и напряжений лещади доменной печи [13].

Известные результаты прочностных расчетов комбинированной

лещади доменной печи получены на основе модели плоского напряжен-

ного состояния упругого диска, подверженного стационарному нагреву.

Однако неравномерность прогрева по высоте создает условия для изгиба

верхних рядов кладки (рис. 26). Это обстоятельство требует специально-

го исследования, во всяком случае для верхнего ряда, поскольку он нахо-

дится в наиболее неблагоприятных условиях. Все ряды кладки работают

независимо друг от друга и расчет остальных рядов в целом аналогичен.

На рис. 27 рассматривается круглая пластина толщиной h, радиу-

сом а, подверженная воздействию температурного поля Т, поперечного

давления q и приложенного по краю радиального изгибающего момента

. В рабочем диапазоне температур упругие характеристики материала

по имеющимся данным ведут себя нелинейно, а поскольку температура

пластины от точки к точке изменяется, то и модуль упругости Е

, и коэф-

фициент теплового расширения α будут зависеть от пространственных

координат z, r, θ (r и θ – соответственно радиальная и окружная полярные

координаты в плоскости пластины, z – нормальная координата, направ-

ленная вертикально вниз). Примем некоторые упрощающие предположе-

ния, которые, хотя и исказят количественные результаты, но не должны

повлиять на качественные.

Рис. 26. Характерное распределение температур в области лещади

Рис. 27. Расчетная схема изгиба верхнего ряда лещади.

1. Верхний слой лещади в пределах металлоприемника в каждом

горизонтальном сечении нагрет практически равномерно. Поэтому целе-

сообразно считать температурное поле Т не зависящим от координат r, θ,

т. е.

T = T(z). (20)

2. Давление шихты и продуктов плавки q также считается равно-

мерно приложенным по всей поверхности слоя в пределах металлопри-

емника.

3. Предполагается, что напряжения, имеющие место в конструк-

ции, не выводят ее в область пластических деформаций. Не рассматри-

ваются также явления ползучести и релаксации.

4. Специфика расчета лещади заключается в том, что огнеупор-

ная кладка способна воспринимать только сжимающие напряжения. По-

этому принимаем, что рассматриваемая пластина изготовлена из разно-

модульного линейно-упругого материала с модулем упругости на сжатие

, величина которого является функцией температуры, и, в силу (20),

=E(z). Коэффициент Пуассона  для кладки считается равным нулю.

Слои огнеупорной кладки, в которых возникают растягивающие напря-

жения, из работы выключаются.

5. Кладка представляет собой газопроницаемый материал, по-

этому внутреннее давление газа ею не воспринимается, а передается не-

посредственно на стальной кожух.

6. Учет переменности упругих характеристик материала по тол-

щине пластины значительно усложняет расчет, поэтому введем осред-

ненные величины

 







dzzE

E ,

           

zdzzTz

T,dzzTz





 . (21)

Считаем, что модуль упругости материала постоянен по толщине

пластины и равен Е, а величины αТ, характеризующие тепловое расши-

рение, распределены по толщине пластины линейно по закону









,TzTT

 (22)

где, как нетрудно видеть, подставив равенство (22) в соотношение (21),

имеем

       

T,TT

M2N1

 (23)

7. Рассматриваемая пластина достаточно жесткая (a/h ~ 7), по-

этому представляется возможным без существенного ущерба для точно-

сти результатов пренебречь мембранными напряжениями, возникающи-

ми вследствие ее изгиба, по сравнению с напряжениями, обусловленны-

ми тепловым распором.

Обозначим u

, v

, w соответственно радиальное, окружное пере-

мещения и прогиб. Тогда, как следует из гипотез Кирхгофа,

   

,,rww,

z,rvv,

z,ruu

























где u, v, w(r,θ) – соответствующие перемещения срединной поверхности.

Мембранные напряжения в пластине обозначим σ

, σ

rθ

и вве-

дем функцию напряжения Ф по формулам

.0,

Фd

dФ





(24)

Формулы (24) учитывают осесимметричность задачи относи-

тельно начала координат, помещенного в центр пластины. Введем также

цилиндрическую жесткость пластины



(учтено, что v=0). Тогда, в силу допущения 7 задача может быть линеари-

зована, и система разрешающих уравнений представляется в виде

 

,TEФ

 (25)

 

,TEhq

dФ

hwD

224















 (26)

где оператор Лапласа













 (27)

Следовательно, согласно допущению 1, в правых частях пропа-

дают слагаемые, содержащие (27). Принимаемые граничные условия от-

ражают взаимодействие центральной (в пределах металлоприемника) и

периферийной частей лещади.

По имеющейся программе расчета футерованного кольца произ-

водится серия расчетов для заданного температурного поля с целью оп-

ределения зависимости напряжений в периферийном кольце от радиаль-

ных смещений его внутреннего диаметра





arz



 .

Для простоты функция f в рассматриваемом диапазоне смещений

может быть аппроксимирована линейной функцией





z10z

uaauf  .

Тогда граничные условия для уравнения (25) таковы: отсутствие

сингулярностей в центре (при r=0); радиальные напряжения по краю пла-

стины уравновешиваются реакцией периферийного кольца, т. е. при r=а



= f(u).

Граничные условия для уравнения (26) формулируются следую-

щим образом: отсутствие сингулярностей в центре пластины; равенство

нулю прогибов по краю: при r=а w = 0, радиальные моменты на краю

пластины уравновешиваются суммой момента М

и реакцией перифе-

рийного кольца М

пкr

MMM  .

Определение М

не вызывает трудностей:







































10arr

zdz

zuaazdz

(28)

Как видно из соотношения (28), момент М

пропорционален углу

поворота опорного сечения.

Момент М

определяется как максимальный, который может

быть воспринят силами трения между отдельными кирпичами кладки, т.

е. как произведение радиальных усилий на коэффициент трения (k

тр

≈

0,4)

и на ширину кирпича (~15 см).

Система (8), (9) с учетом принятых граничных условий позволя-

ет получить решение в замкнутом виде:





 









   

aaJaJ

aJrJ





















 ,

 













 zSTT

 













   

aaJaJ

rJrrJ















































 ,

 

















zATT

 









   

aaJaJ

rrJ















































 ,

где





 

Ehaa1

Taaa









Очевидно, что эти формулы имеют смысл лишь в том случае, ко-

гда в результате оказывается w(r) ≤ 0. Нагрузку, соответствующую w|

r=0

0, назовем нагрузкой прижатия q

, тогда результаты имеют смысл при q

< q

. Если при этом пластина полностью обжата как по радиусу, так и по

толщине, расчет можно считать оконченным. В противном случае его

необходимо повторить, исключив из работы растянутые участки.

Расчеты производились для двух тепловых режимов, соответст-

вующих по времени 96 ч от начала работы печи, когда тепловое поле еще

не окончательно установилось, и весьма далеким моментам времени, ко-

гда тепловое поле можно рассматривать как стационарное.

а б

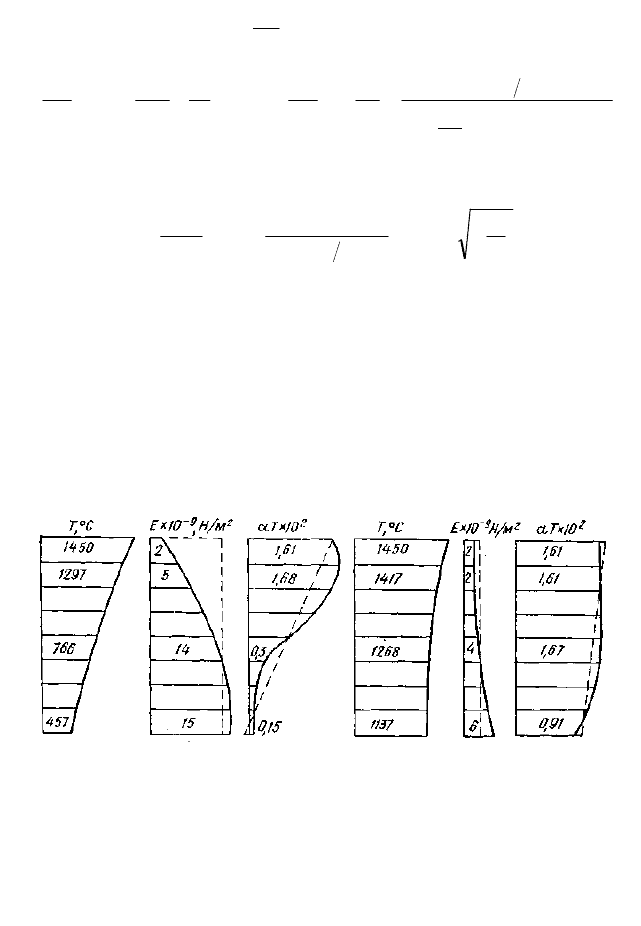
Рис. 28. Изменение Т, Е, αТ по толщине: а – в режиме 96 ч, б – в стационарном

режиме

Согласно указанным выше данным, расчетные случаи могут

быть представлены в виде эпюр, приведенных на рис. 28, а, б. На тех же

рисунках штрихпунктирными линиями показаны величины и зависимо-