Doktorov E.V., Leble S.B. A Dressing Method in Mathematical Physics
Подождите немного. Документ загружается.


8.3 Modified nonlinear Schr¨odinger equation 239
and, second, a formula for the reconstruction of the potential Q,
Q =
2
α
σ
3
Φ
(1)
+
Φ
(0)−1
+
. (8.45)
In virtue of the involution of the type (8.10) we introduce a matrix function
Φ
−1
−
,
Φ
−1
−
(x, k)=Φ
†
+
(x,
¯
k), (8.46)
which is analytic for Im k
2
< 0, i.e., in the second and fourth quadrants.
This domain is denoted as C
−
. These formulas give the following relations for
determinants:
det Φ
+
(x, k)=a(k), det Φ
−1
−
(x, k)=¯a(k).
As follows from (8.45), we need to know explicitly the matrix Φ
+
to find
solutions of the MNLS equation.
8.3.3 Matrix R H problem
Once again we calculate a product Φ
−1
−
(x, k)Φ
+
(x, k)fork ∈ Im k
2
=0,
Φ
−1
−
(x, k)Φ
+
(x, k)=EG
0
(k)E
−1
, (8.47)
where
G
0
(k)=S
†
+
S
+
=
1
¯
b
b 1
.
Hence, we obtain the RH problem (8.5). Figure 8.1 illustrates the contour L
dividing the complex k-plane into two domains C
+
and C
−
with the Φ
+
func-
tion and the Φ
−1
−
function, respectively. The positive direction o f the contour
k
÷
++
()M
÷
++
()M
÷
-
(M
-
-1
)
÷
-
(M
-
-1
)
L
Fig. 8.1. Domains of analyticity and the contour L direction

240 8 Dressing via local Riemann–Hilbert problem
corresponds to the rule that the C
+
domain is on the left when traveling along
the contour. The normalization of the RH problem (8.47) is noncanonical be-
cause, in accordance with (8.43),
Φ
+
(x, k) → Φ
(0)
+
(x),k→∞.
In general we obtain the RH problem with zeros. Suppose that all zer os
are simple. In virtue of the involution (8.46) we have an equal number N of
zeros in C
+
and C
−
. Moreover, because of the par ity property (8.40), zeros
appear in pairs as ±k
j
and ±
¯
k
l
. This means that the regularization of the RH
problem at the points ±k
j
is performed by two elementary rational multipliers,
Φ
+
Ξ
−1
j
Ξ
−1
−j
,where
Ξ
−1
j
= 11+
k
j
−
¯
k
j
k −
¯
k
j
P
j
,Ξ
−1
−j
= 11 −
k
j
−
¯
k
j
k +
¯
k
j
P
−j
,P
±j
=
|χ
±j
χ
±j
|
χ
±j
|χ
±j
,
and Φ
+
(±k
j
)|χ
±j
= 0. In virtue of the parity property, the vectors |χ
j
and |χ
−j
are interrelated, |χ
−j
= σ
3
|χ
j
, and th erefore P
−j
= σ
3
P
j
σ
3
.
After the complete regularization, we once again arrive at the factorizable
representation of Φ
±
,
Φ
±
= φ
±
Γ, Γ = Ξ
N
Ξ
−N
···Ξ
1
Ξ
−1
, (8.48)
where φ
±
solve the regular RH problem
φ
−1
−
φ
+
= ΓEG
0
E
−1
Γ
−1
. (8.49)
Comparing the asymptotic expansion
Γ (x, k)=
11+k
−1
Γ
(1)
(x)+O(k
−2
)
with that for Φ
+
(8.43), we obtain from (8.48)
Φ
(0)
+
= φ
+
,Φ
(1)
+
= Φ
(0)
+
Γ
(1)
.
Hence, we can take the leading-order term Φ
(0)
+
(x) of the asymptotic expansion
(8.43) as a k-independent solution of the regular RH problem. In turn, the
reconstruction formula (8.45) now takes the form
Q =
2
α
Φ
(0)
+
Γ
(1)
!
Φ
(0)
+
"
−1
. (8.50)
Note that because the RH problem for the NLS equation allows the standard
normalization, we took a trivial solution (φ
+
= 11) of the regular RH problem
(8.19). It should be stressed once again that a choice of a k-independent
solution of the regular RH problem is valid for solitons only. If we want to
account for the nonsolitonic part of a solution, we should consider a nontrivial
solution of the regular RH problem. As a rule, the r egular RH problem do es

8.3 Modified nonlinear Schr¨odinger equation 241
not allow as complete an analytical investigation as the RH problem with
G
0
= 11. In general, the regular RH problem can be formulated in terms of
singular integral equations. Examples of a p erturbative study of the regular
RH problem to account for soliton radiation are given in [122, 398]. The
description of the RH problem for the WKI spectral problem can be also
found in the paper by Zabolotskii [463].
8.3.4 MNLS soliton
We can simplify the reconstruction formula (8.50) when soliton solutions are
concerned. Indeed, equations (8.39), (8.44), and (8.48) yield the equation for
the dressing factor:
Γ
x
=
!
Φ
(0)−1
+
Φ
+
"
x
=
iα
2
Q
2
σ
3
Γ −
i
2
(k
2
− 1) [σ
3
,Γ]+ik
!
Φ
(0)
+
"
−1
QΦ
(0)
+
.
Therefore, Γ
−1
(x, k =0)obeys
Γ
−1
(x, k =0)
x
= −
iα
2
Q
2
σ
3
Γ
−1
(x, k =0).
But exactly the s ame differential equation occurs for Φ
(0)
+
; see (8.44). Hence,
we can identify Γ
−1
(x, k =0)andΦ
(0)
+
and write the reconstruction formula
(8.50) for solitons as
Q =
2
α
σ
3
Γ
−1
(k =0)Γ
(1)
Γ (k =0). (8.51)
As a result, it is the dressing factor Γ that completely deter mines soliton
solutions of the MNLS equation.
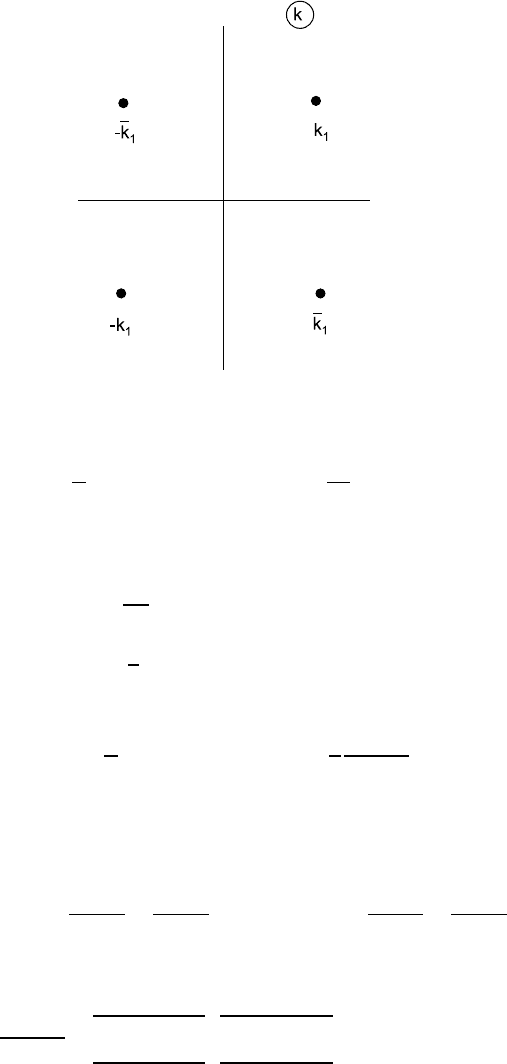
Now we will derive the MNLS soliton. The discrete data of the RH problem
comprise the eigenvalues k
1
, k
2
= −k
1
,
¯
k
1
,and
¯
k
2
= −
¯
k
1
(Fig. 8.2), as well
as the eigenvectors |1 and |2≡|−1 = σ
3
|1. Following (8.23) and (8.24),
we have
Γ (k)=11 −
1
k −
¯
k
1
D
−1
11
|11| +
D
−1
21
|21|
−
1
k +
¯
k
1
D
−1
12
|12| +
D
−1
22
|22|
,
Γ
−1
(k)=11+
1
k − k
1
D
−1
11
|11| +
D
−1
12
|12|
+
1
k + k
1
D
−1
21
|21| +
D
−1
22
|22|
.
Hence, we need know the eigenvectors to obtain the matrix elements D
lj
(8.23)
and the dressing factor Γ . In the same way as was done for the NLS equation
in (8.26) and (8.27), we have a system of linear equations for the vector |1:
242 8 Dressing via local Riemann–Hilbert problem
Fig. 8.2. Typical arrangement of zeros corresponding to the MNLS soliton
|1
x
= −
i
α
(k
2
1
− 1)σ
3
|1, |1
t
= −
2i
α
2
(k
2
1
− 1)
2
σ
3
|1.
Solving it we obtain the vector |1 exactly in the form (8.31) but with different
definitions of z and ϕ.Namely,
z =
1
2w
(x − Vt− x
0
) ,x
0
=2aw,
ϕ = Vwz+
1
4
(V
2
+ w
−2
)t + ϕ
0
,ϕ
0
= aV w + β.
Here we have introduced real parameters V and w,
V =
2
α
(2 − k
2
1
−
¯
k
2
1
),w=
i
2
α
k
2
1
−
¯
k
2
1
,
which play the role of the soliton velocity and width, as will be seen later.
Note once again that |2 = σ
3
|1. Therefore, we can now calculate the matrix
D in accordance with (8.23) and represent Γ and Γ
−1
as
Γ (k)=11 −
˜
D
−
k −
¯
k
1
−
˜
D
+
k +
¯
k
1
,Γ
−1
(k)=11+
D
−
k − k
1
+
D
+
k + k
1
.
Here
D
−
=
k
2
1
−
¯
k
2
1
2
⎛
⎜
⎜
⎝
e
z
k
1
e
z
+
¯
k
1
e
−z
e
iϕ
k
1
e
−z
+
¯
k
1
e
z
e
−iϕ
k
1
e
z
+
¯
k
1
e
−z
e
−z
k
1
e
−z
+
¯
k
1
e
z
⎞
⎟
⎟
⎠
,D
+
= −σ
3
D
−
σ
3
,
8.3 Modified nonlinear Schr¨odinger equation 243
˜
D
−
=
k
2
1
−
¯
k
2
1
2
⎛
⎜
⎜
⎝
e
z
k
1
e
−z
+
¯
k
1
e
z
e
iϕ
k
1
e
−z
+
¯
k
1
e
z
e
−iϕ
k
1
e
z
+
¯
k
1
e
−z
e
−z
k
1
e
z
+
¯
k
1
e
−z
⎞
⎟
⎟
⎠
,
˜
D
+
= −σ
3
˜
D
−
σ
3
.
This gives
Γ
(1)
= −
!
˜
D
+
+
˜
D
−
"
=(k
2
1
−
¯
k
2
1
)
⎛
⎜
⎜
⎝
0
e
iϕ
k
1
e
−z
+
¯
k
1
e
z
e
−iϕ
k
1
e
z
+
¯
k
1
e
−z
0
⎞
⎟
⎟
⎠
,
Γ (k =0)=
k
1
¯
k
1
⎛
⎜
⎜
⎝
k
1
e
z
+
¯
k
1
e
−z
k
1
e
−z
+
¯
k
1
e
z
0
0
k
1
e
−z
+
¯
k
1
e
z
k
1
e
z
+
¯
k
1
e
−z
⎞
⎟
⎟
⎠
.
Substituting these matrices into (8.51) eventually yields the soliton of the
MNLS equation:
u
s
(x, t)=
i
w
k
1
e
−z
+
¯
k
1
e
z
(k
1
e
z
+
¯
k
1
e
−z
)
2
e
iϕ
. (8.52)
The most important feature of the soliton (8.52) consists in the fact that the
parameter α enters the denominator of (8.52) through w. This means that the
soliton (8.52) is nonperturbative with respect to α and cannot be obtained by
considering the MNLS equation as an α-perturbed NLS equation. Despite a
rather unaccustomed form, it is easy to check that the mo dulus of the soliton
(8.52) behaves as prescribed for solitons, i.e., mainly in accordance with the
hyperbolic secant rule:
|u
s
| =
sech z
2w|k
1
|cos θ
1+tan
2
θ tanh
2
z
−1/2
.
Here
|k
1
| =
(
!
1 −
α
4
V
"
2
+
!
α
4w
"
2
)
1/4
, tan 2θ =
α
4w
1
1 − (α/4)V
.
The soliton (8.52) has a number of peculiarities which distinguish it from the
standard NLS soliton. First, the soliton u
s
has nonzero phase difference at its
limits. Indeed,
k
1
e
−z
+
¯
k
1
e
z
(k
1
e
z
+
¯
k
1
e
−z
)
2
−→
(
¯
k
1
/k
2
1
)e
−z
,z→∞
(k
1
/
¯
k
2
1
)e
z
,z→−∞
and
arg (u
s
(z →−∞)) − arg (u
s
(z →∞)) = 6 arg(k
1
) =0.

244 8 Dressing via local Riemann–Hilbert problem
Second, the important invariant of the MNLS equation, namely, the optical
energy (or number of particles)
∞
−∞
|u
s
|
2
dx, has the upper limit [399]
∞
−∞
|u
s
|
2
dx =
8
α
arg(k
1
) <
4π
α
.
These properties of the MNLS soliton resemble tho se of the dark NLS soli-
ton which also has nonzero phase difference and relation between the optical
energy and the phase difference.
At the same time, there exists a nontrivial limit transition from the MNLS
soliton to the bright NLS one. To carry out this limit, we should take into
account that the Lax pair (8.38) f or the MNLS equation should produce in
this limit the Lax pair (8.7) for the NLS equation. This condition implies that
the spectral parameter k depends on α and gives the following prescription
[399]:
1
α
(k
2
− 1) −→ k
NLS
at α → 0,
or
k =1+
α
2
k
NLS
+ O(α
2
) . (8.53)
In the limit (8.53) the MNLS soliton (8.52) reproduces the NLS soliton (8.32).
Similarly to the NLS equation, we can construct a MNLS breather by
means of the dressing factor Γ with N = 4 because o f zeros ±k
1
and ±k
2
(as well as ±
¯
k
1
and ±
¯
k
2
). Explicit calculation was performed by Doktorov
[121]. Figures 8.3 and 8.4 demonstrate the temporal evolution of the MNLS
breather. We see that the MNLS breather evolves as a whole object, without
any decomposition into single solitons, as it should.
-4
-2
0
2
4
x
0
2
4
6
8
10
12
14
16
18
20
22
24
t
-3
-2
-1
0
1
2
3
Fig. 8.3. Evolution of the real part of the MNLS breather

8.4 Ablowitz–Ladik equation 245
-4
-2
0
2
4
x
0
2
4
6
8
10
12
14
16
18
20
22
24
t
-4
-3
-2
-1
0
1
2
3
Fig. 8.4. Evolution of the imaginary part of the MNLS breather
8.4 Ablowitz–Ladik equation
This section is devoted to a consideration of a completely different example
of nonlinear integrable e quations, namely, the discrete nonlinear AL equation
[8]. The propagation properties of waves arising as a result of the interplay
of nonlinearity with the lattice discreteness can be quite distinct from those
inherent in continuous nonlinear systems. For example, self-focusing and defo-
cusing processes can be achieved in the same discrete medium, and wavelength
diffraction management [9], the possibility forbidden in c ontinuous systems,
is possible. Our aim in this section is to derive the so li ton solution of the AL
equation. We will follow prescriptions developed in the preceding s ections and
will see that, despite some features peculiar to discrete eq uations, the main
ideas of the dressing method based on the RH problem are valid for a wide
class of nonlinear equations, no matter whether the coor dinates are discrete
or continuous. Moreover, a striking resemblance exists between solving the
MNLS and AL equations, though it is the NLS equation that represents the
continuous limit of the AL equation.
8.4.1 Jost solutions
The AL equation
iu
nt
+
1
h
2
(u
n+1
+ u
n−1
− 2u
n
)+|u
n
|
2
(u
n+1
+ u
n−1
) = 0 (8.54)
describes evolution of a scalar complex function u
n
(t) defined on an infinite
one-dimensional lattice (−∞ <n<∞) with the lattice spacing h.Theterms

246 8 Dressing via local Riemann–Hilbert problem
u
n+1
+ u
n−1
− 2u
n
represent the discrete analog of t h e second derivative. To
perform a limit h → 0, we write u
n±1
as
u
n±1
= u ± hu
x
+
1
2
h
2
u
xx
and substitute them into (8.54). This yields the NLS equation iu
t
= u
xx
+
2|u|
2
u. In the following we put h =1.
The AL equation allows the Lax representation with the AL spectral prob-
lem [8]
J(n +1)=(E + Q
n
)J(n)E
−1
, (8.55)
Q
n
=
0 u
n
−u
∗
n
0
,E=
z 0
0 z
−1
,
and the evolutionary equation
J
t
(n)=V (n)J(n) − J(n)Ω(z), (8.56)
V (n)=i
u
∗
n−1
u
n
zu
n
− z
−1
u
n+1
z
−1
u
∗
n
− zu
∗
n−1
−u
n−1
u
∗
n
+ Ω,
Ω (z)=
i
2
(z − z
−1
)
2
σ
3
.
It is customary to denote a spectral parameter for the AL spectral problem
as z, instead of k in the preceding sections. Besides, for further convenience
we use here an asterisk to denote complex conjugation.
Note that we encounter the first novel feature compared with continu-
ous equations. Indeed, the spectral problem (8.55) is not differential but al-
gebraical. Nevertheless, we can introduce matrix Jost functions J
±
(n, z)as
solutions of the spectral equation (8.55) with the asymptotics J
±
→ 11as
n →±∞. The scattering matrix S(z) defined by
J
−
(n, z)=J
+
(n, z)E
n
S(z)E
−n
(8.57)
has the structure
S(z)=
a
+
−b
−
b
+
a
−
.
The AL sp ectral problem, like the WKI one, obeys the parity property
J(n, z)=σ
3
J(n, −z)σ
3
. (8.58)
Hence, we can suppose tha t the process of solving the AL equation will have
much in common with that of the MNLS equation, and not with that of the
NLS equation, as one might expect.
The second feature is the lack of a simple involution relation like (8.10).
Instead we will now derive a discrete analog of the involution property. To
this end, let us define a parameter ¯z as ¯z =1/z
∗
. Then it is easy to show that
(E(¯z)+Q
n
)
†
= E
−1
(z) − Q
n
and
[J
±
(n +1, ¯z)]
†
=
(E(¯z)+Q
n
) J
±
(n, ¯z)E
−1
(¯z)
†
=E(z)J
±
(n, ¯z)
E
−1
(z)− Q
n
.
8.4 Ablowitz–Ladik equation 247
Accounting for the relation [E
−1
(z) −Q
n
](E + Q
n
)=(1+|u
n
|
2
) 11, we obtain
J
†
±
(n +1, ¯z) J
±
(n +1,z)=(1+|u
n
|
2
)EJ
†
±
(n, ¯z) J
±
(n, z)E
−1
.
Iterating this relation as
J
†
±
(n, ¯z) J
±
(n, z)=(1+|u
n
|
2
)E
−1
J
†
±
(n +1, ¯z) J
±
(n +1,z)E
=(1+|u
n
|
2
)
−1
(1 + |u
n+1
|
2
)
−1
E
−2
J
†
±
(n +2, ¯z) J
±
(n +2,z)E
2
= ...
and taking into account the asymptotic behavior J
+
→ 11atn → +∞ even-
tually yields
J
†
+
(n, ¯z)J
+
(n, z)=
∞
l=n
ρ
−1
l
11 ,
where ρ
l
=1+|u
l
|
2
.Denoting
∞
l=n
ρ
−1
l
= v
+
(n), (8.59)
we can write the result of iterations as
J
†
+
(n, ¯z)=v
+
(n) J
−1
+
(n, z). (8.60)
In the same way we obtain
J
†
−
(n, ¯z)=v
−
(n)J
−1
−
(n, z),v
−
(n)=
n−1
l=−∞
ρ
l
. (8.61)
Equations (8.60) and (8.61) determine the involution property for the AL
spectral problem. We will call the relations (8.60) and (8.61) as conjugation.
Now we show that the functions v
±
(n) are nothing more than determinants of
J
±
. Indeed, because det (E +Q
n
)=ρ
n
,wehavedetJ
+
(n+1) = ρ
n
det J
+
(n),
or
det J
+
(n)=ρ
−1
n
det J
+
(n +1)= ρ
−1
n
ρ
−1
n+1
det J
+
(n +2)=... =
∞
l=n
ρ
−1
l
= v
+
,
and similarly for J
−
.Asaresult,detJ
±
(n, z)=v
±
(n). It should be noted in
this connection that det J
−
(n)=detJ
+
(n)detS and hence
det S = v, v = v
−1
+
v
−
=
∞
l=−∞
ρ
l
.
The next step in studying the Jost solutions is their asymptotic behavior.
Let us write the spectral equation (8.55) in the explicit form
J
11
J
12
J
21
J
22
n+1
=
J
11
+ z
−1
u
n
J
21
z
2
J
12
+ zu
n
J
22
z
−2
J
21
− z
−1
u
∗
n
J
11
J
22
− zu
∗
n
J
12
n

248 8 Dressing via local Riemann–Hilbert problem
and consider the limit z →∞,forwhichJ(n, z)=J
(0)
(n)+z
−1
J
(1)
(n)+
z
−2
J
(2)
(n)+... . Then in the leading order of the asymptotic expansion we
obtain
J
(0)
11
J
(0)
12
J
(0)
21
J
(0)
22
n+1
=
J
(0)
11
z
2
J
(0)
12
+ zJ
(1)
12
+ zu
n
J
(0)
22
0 J
(0)
22
− zu
∗
n
J
(0)
12
− u
∗
n
J
(1)
12
n
.
Comparing the entries with the same power of z on both sides of this relation,
we get
J
(0)
(n +1)=
10
0 ρ
n
J
(0)
(n) , (8.62)
while the potential u
n
is retrieved as
u
n
= −
J
(1)
12
J
(0)
22
. (8.63)
In the limit z → 0, for which J(n, z)=J
(0)
(n)+zJ
(1)
(n)+z
2
J
(2)
(n)+...,
we similarly obtain
J
(0)
(n +1)=
ρ
n
0
01
J
(0)
(n).
8.4.2 Analytic solutions
To reveal analytic properties of the Jost solutions, we rewrote the spectral
equation for the continuous nonlinear equations in the form of integral equa-
tions. Now it is natural to use infinite products. Indeed, we transform the
spectral equation as
J(n, z)=(E + Q
n
)
−1
J(n +1,z)E =
E
−1
− Q
n
ρ
n
J(n +1,z) E
= lim
N→∞
N
l=n
E
−1
− Q
l
ρ
l
J(N +1)E
N−n+1
and for the first column we write
J
[1]
+
(n, z)=[J
+
(n, z)]
·1
= lim
N→∞
N
l=n
E
−1
− Q
l
ρ
l
··
[J
+
(N +1)]
·1
z
N−n+1
.
Since J
+
(N) → 11atN →∞,thefactor[J
+
(N +1)]
·1
in the last equa-
tion can be treated as [ J
+
(N +1)]
11
. Hence, the expression in parentheses
does not contribute to the z-dependence of J
+21
and therefore [J
+
(n, z)]
21
∼
z
N−n+1
−→ 0atz → 0. As regards J
+11
, we will gain z
−1
=(E
−1
)
11
from
every factor in the product, which r esults in J
+
(n, z)
11
∼ z
−(N−n+1)
z
N−n+1
