Doktorov E.V., Leble S.B. A Dressing Method in Mathematical Physics

Подождите немного. Документ загружается.

8.5 Three-wave resonant interaction equations 259

where

∆



l=1

(0)

exp[2η

x + b

t)].

To gain greater insight into the solution (8.90), let us consider the case

of only two nonzero constants p

(0)

and p

(0)

; hence, the potential U contains

only two nonzero entries u

and u

=¯u

. In this case the solution (8.90)

transforms to

=iη

− a

)

exp {−ξ

[(a

− a

)x +(b

− b

)t + φ

]}

cosh [η

− a

)(x − v

t − x

)]

, (8.91)

where

− α

− a

,φ

− φ

(0)

≡ exp (α

+iφ

This result is somewhat trivial because only one of the wave packets has a

nonzero envelope, but th e essential features of such a solution are inherent in

the whole soliton (8.90). Indeed, let all p

(0)

be nonzero. Consider the solution

(8.90) for t →∞, paying special attention to the wave u

. We can put u

in the following form:

=2iη

− a

)exp{−iξ

[(a

− a

)x +(b

− b

)t + φ

]}D

−1

, (8.92)

where

=2cosh[η

− a

)(x − v

t)+α

− α

]

+exp[−η

− a

)(x − v

t) − α

+ α

]exp[η(a

− a

)(x − v

t)+α

− α

] .

Let v

. Then we conclude from (8.92) that u

→ 0fort →∞, while for

t →−∞u

tends to the expression of the type (8.91) with the change of in-

dices 2 → 3, i.e., to the soliton of pumping wave. In contrast, the components

and u

tend exponentially to zero for t →−∞and to solitons of the

type (8.91) for t →∞. Thereby, the solution (8.90) describes the decay of the

composite soliton into two simple ones. For the case of v

the solution

(8.90) describes the reverse process of a fusion of two simple solitons into the

composite on e.

Hence, the three-wave resonant interaction process provides an example

of the so-called nontrivial interaction of solitons, as distinct from the trivial

interaction (scattering) of the NLS solitons.

So far we have considered the case of the simplest identity reduction

†

= U. At the same time, the spectral problem (8.82) allows a reduction

of a more general type (the so-called B-hermiticity [354]):

†

= BUB, B =diag(r

260 8 Dressing via local Riemann–Hilbert problem

where r

= ±1. Such a reduction provides the mutual conjugation of zeros of

the RH problem which lie in diﬀerent half planes of the k-plane. It is easy to

see that the projective matrix P takes the form

¯p



It is important that nonidentity reduction leads to a substantial modiﬁcation

of the above results. This conclusion follows from the fact that the denomi-

nator ∆

entering the soliton solution (8.90) takes the form

∆

′



l=1

(0)

exp [ 2η

x + b

t)]. (8.93)

If some of r

are equal to −1, a singularity o ccurs for some values of the

coordinates. Let us consider the case B =(−1, 1, 1). It is evident that the

singularity is absent only for p

(0)

= 0, which means that only the soliton of

thesimplewaveu

exists in the system with such a restriction. A similar

conclusion follows for the reduction matrix B =(1, 1, −1).

Nontrivial results take place for the reduction B =(1, −1, 1). As for the

previous cases, we have here the possibility of the existence of solitons of the

wave u

for two other zero waves. At the same time, a general solution for

three envelopes can exist, but for a ﬁnite time interval. Indeed, let us write

the denominator ∆

′

(8.93) in the form

∆

′

exp [ 2α

+2η

x + b

t)]

=1− exp [ 2(β

− β

) −2η

− a

)x − 2η

− b

)t]

+exp[2(β

− β

) −2η

− a

)x − 2η

− b

)t]

and analyze the expression on the right-hand side. This analysis shows that

under the condition

− a



|β

− β

− a

− (b

− b



− a



|β

− β

− a

− (b

− b



∆

′

does not take zero value. Excluding the exceptional case v

= v

,wesee

that this inequality is broken for some positive or negative t = t

.Thecaseof

the positive t

corresponds to the explosive instability, while for the negative

we have the process of smoothing the initial singularity.

Note that the Darboux-dressing transformation was applied in [108] to

construct a larger class of exact solutions of the three-wave equations with

nontrivial seed solutions.

8.6 Homoclinic orbits via dressing method 261

8.6 Homoclinic orbits via dressing method

In this section we will dress nonzero solutions of the NLS and MNLS equa-

tions. Along with solitons as stable solutions of nonlinear integrable equations

with important applications in physics and mathematics, these equations al-

low unstable waves such as homoclinic orbits. The existence of homocli n ic

solutionsservesasanindicatorofchaotic behavior in a perturbed deter-

ministic nonlinear dynamical system. The role of homoclinic solutions in the

generation of chaos was r evealed in the case of per iodic boundary conditions

for the damped-driven sine–Gordon equation [326, 327] and for the perturbed

NLS equation [5, 11, 6, 201, 297]. Extended reviews of analytic and numerical

metho ds in this topic are given by McLaughlin and Overman [328] and by

Ablowitz et al. [6]. Diﬀerent approaches have been proposed for derivation of

homoclinic solutions for i ntegrable partial diﬀerential equations: while the bi-

linear Hirota method [210] was used by Ablowitz and Herbst [5], the B¨acklund

transformations were employed in [296, 326, 327, 455]. The problem of con-

struction of the homoclinic orbits by means of the Darboux transformation

method is discussed in the book of Matveev and Salle [324].

We will show in this section that the dressing method develop ed in the

preceding sections i s well suited to derive homoclinic solutions. In order to

explain basic ideas, we ﬁrst reproduce the known homoclinic solution of the

NLS equ ation by means of the dressing method. Then we consider the MNLS

equation.

8.6.1 Homoclinic orbit for NLS equation

The NLS equation

= u

+2(|u|

− ω)u, ω ∈ Re (8.94)

with an additional real parameter ω has the Lax pair ψ

= Uψ and ψ

= Vψ

with the matrices U and V of the form

U =ikσ

+iQ, Q =



0 u

¯u 0



V =i(2k

− Q

+ ω)σ

+2ikQ + σ

We are interested in periodic solutions of (8.94) with a spatial perio d L,

u(x + L, t)=u(x, t). Hence, the Floquet theory should b e applied to the

spectral equation ψ

= Uψ. The fundamental matrix M (x, k) is deﬁned as a

solution of the spectral equation with the boundary condition M(0,k)=11.

The Floquet discriminant is deﬁned as ∆(k)=trM(L, k), where M (L, k)

is the transfer matrix, and bounded eigenfunctions of the spectral problem

correspond to ∆(k) satisfying the condition −2 ≤ ∆(k) ≤ 2. The Floquet

spectrum is characterized by the simple periodic points {k

, ∆(k

)=±2,

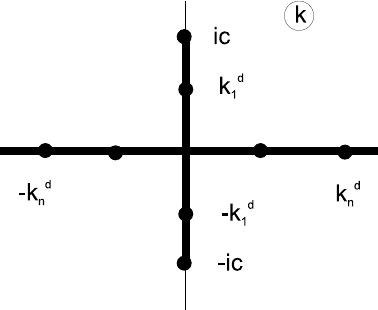
262 8 Dressing via local Riemann–Hilbert problem

(d∆/dk)

=0} and the double points {k

, ∆(k

)=±2, (d∆/dk)

=0,

∆/dk

)

=0}. We will deal with the complex double points indicating

linearized instability of s olutions of a nonlinear wave equation because these

points label the orbits homoclinic to unstable solutions.

We are interested in orbits homoclinic to the periodic plane wave solution

of the NLS equation (8.94) taken in the form

= c exp[−2i(c

− ω)t], (8.95)

where c is a real amplitude. Simple calculation gives the fundamental matrix,

M(x, k)=



cos μx +i(k/μ)sinμx i(c/μ)e

−2i(c

−ω)t

sin μx

i(c/μ)e

2i(c

−ω)t

sin μx cos μx − i(k/μ)sinμx



,μ

= c

and hence ∆(k)=2cosμL. Thereby, the Floquet spectrum comprises the

real axis of the k-plane (the main spectrum) and a part of the imaginary axis

lying between the simple periodic points ±ic. Besides, there exists an inﬁ n ite

sequence of real double points k

=[(nπ/L)

− c

]

1/2

,wherec

≤ (nπ/L)

and n are integers, and a ﬁnite number of complex double points k

,where

j are integers, situated on the imaginary axis within the interval (ic, −ic),

(jπ/L)

. In what follows we choose c and L in such a way to obtain a

single pair of complex double points k

= ±i[c

−(π/L)

]

1/2

, which is a single

unstable mode of the solution (Fig. 8.6). Hence, j =1andn =2, 3,...

After diagonalization of the transfer matrix M(L, k), R

−1

M(L, k)R =

diag(e

iμL

, e

−iμL

), we deﬁne the Blochsolution ˜χ = M(x, k)R of the spectral

Fig. 8.6. The Floquet spectrum (thick lines), inﬁnite sequence of the real double

points ±k

, simple periodic points ±ic, and the single pair of the complex double

points ±k

8.6 Homoclinic orbits via dressing method 263

equation. Demanding the Bloch solution to satisfy both equations of the Lax

pair, we obtain it explicitly as

˜χ =exp[−i(c

− ω)tσ

]

⎛

⎜

⎝

1 −

μ − k

⎞

⎟

⎠

exp[iμ(x +2kt)σ

] .

In the following, it will be more convenient to work with a modiﬁed Bloch

function χ =˜χ exp[−ikxσ

− i(2k

+ ω)tσ

] which satisﬁes the equations

= Uχ− ikχσ

,χ

= Vχ− i(2k

+ ω)χσ

(8.96)

and allows the asymptotic expansion started with the unit matrix, χ =

11+

−1

(1)

+ O(k

−2

), while the potential Q is r econstructed via

Q = −[σ

,χ

(1)

]. (8.97)

Suppose now that a solution homoclinic to the plane wa ve (8.95) can be

obtained from (8.97) with the Bloch function χ being a result of dressing the

Bloch function χ

which satisﬁes (8.96) with u = u

χ = Γχ

. (8.98)

Here Γ (k, x, t) is the dressing factor which is written in the form well known

for us:

Γ = 11 −

−

k −

P, Γ

−1

= 11+

−

k − k

P, (8.99)

where P is a projector, P =(|11|)/1|1, 1| = |1

†

,and|1 =(p

)

is a

two-component vector. As regards the choice o f the p o le k

in (8.99), it is the

point where we encounter a crucial diﬀerence from the standard applications

of the dressing method. The positions of the poles in the dressing factors are

usually taken quite arbitrarily, without reference to the seed solution u

.In

contrast, it is the seed solution u

which determines these poles in our case.

Namely, we take the complex double points as the poles of the dressing factors;

therefore, k

= k

Expanding (8.99) in the asymptotic series in k

−1

gives a new solution in

terms of the old one and the dressing factor:

Q = Q

− [σ

,Γ

(1)

where Γ = 11+k

−1

(1)

+ O(k

−2

). Hence, we need know the vector |1 to

obtain new solution Q.

Diﬀerentiating (8.98) in x yields

U(k)=−Γ [∂

− U

(k)]Γ

−1

, (8.100)

where U

= U(u

). Evidently, the left-hand side of (8.100) is regular at points

and

, while the right-hand side has simple poles at these points because of

264 8 Dressing via local Riemann–Hilbert problem

the dressing factors. From the condition of a vanishing residue at the point k

we obtain |1

= U

)|1, and, similarly, |1

= V

)|1. These equ ations

are easily integrated and we obtain

|1=e

−i(c

−ω)tσ

⎛

⎜

⎝

A exp(iμ

x − 2k

t) −

− ik

exp(−iμ

x +2k

− ik

exp(iμ

x − 2k

t)+exp(−iμ

x +2k

⎞

⎟

⎠

Here A =const,μ

= μ(k

),k

=ik

.Evidently,Γ

(1)

= −(k

−

)P and

hence u = u

+2(k

−

,withP

=(p

¯p

)/(|p

+ |p

). Inserting here

the vector |1 and intro ducing notations

A =exp(ρ +iβ),τ= σt −ρ, φ = β −π/2,σ=4k

,μ

+ik

= ce

we obtain the homoclinic solution in the form

cos 2p − sin p sech τ cos(2μ

x + φ) − isin2p tanh τ

1+sinp sech τ cos(2μ

x + φ)

−2i(c

−ω)t

(8.101)

which coincides with the solution obtained by Li and McLaughlin [297] by

means of the B¨acklund transformation.

It is easy to see that this solution is indeed homoclinic to the plane wave,

reproducing this wave (up to a factor) at both inﬁnities:

t →±∞: u

→ exp(±2ip)c exp[−2i(c

− ω)t] .

Solutions of the type (8.101) with the plane-wave asymptotic behavior were

previously obtained in [20, 217]. In [20] the solution (8.101) was r elated with

the long-time evolution of the modulational instability of the plane wave. The

Darboux transformation was applied in [217] to dress the plane wave and the

dressedsolutionwasinterpretedasdescribing a process of self-excitation and

subsequent attenuation of periodic waves.

In the case of N unstable modes the above procedure can be iterated.

However, a more eﬃcient way to deal with multiple double points is described

in the next subsection.

8.6.2 MNLS equation: Floquet spectrum and Bloch solutions

The MNLS equation

= u

+iα(|u|

+2(|u|

− ω)u,

with a real constant ω, allows the Lax representation with the matrices U and

V of the form (Sect. 8.3)

U =iΛσ

+ikQ, Λ(k)=

(1 − k

),Q=



0 u

¯u 0



V =iΩσ

+2ikΛQ − ik

+ kσ

+iαkQ

,Ω(k)=2Λ

+ ω.

8.6 Homoclinic orbits via dressing method 265

Like the NLS equation, we take the plane wave solution of the MNLS equation

= c exp[−2i(c

− ω)t]

as a peri odic solution with a spatial p eriod L. The fundamental matrix

M(x, k) is obtained in the form

M(x, k)=

⎛

⎜

⎝

cos μx +i

sin μx i

−2i(c

−ω)t

sin μx

2i(c

−ω)t

sin μx cos μx − i

sin μx

⎞

⎟

⎠

where μ =(Λ

+ c

)

1/2

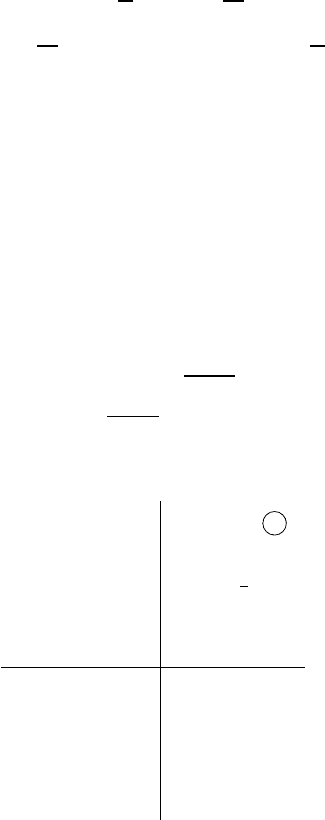
. Hence, ∆(k)=2cosμL and four complex double

points k

= ±[1 − (1/2)α

± iαcl

]

1/2

, l

=[1− (1/4)α

− (jπ/cL)

]

1/2

lying in four quadrants of the k-pla n e, correspond to each unstable mode.

We choose c and L insuchawaythatonlythesingleunstablemodeexists,

i.e., l

> 0andl

< 0forj>1. The linearized stability analysis conﬁrms

that the above four complex double points k

=[1− (1/2)α

− iαcl

]

1/2

= −k

, k

and k

= −

(Fig. 8.7) are associated with the exponential

instability.

The Bloch function which solves both Lax equations takes a surprisingly

simple form:

˜χ

(k, x, t)=exp[−i(c

−ω)tσ

]

⎛

⎜

⎝

1 −

μ − Λ

⎞

⎟

⎠

exp

iμ



x +(2Λ + αc



-k

Fig. 8.7. Four complex double points for the single unstable mo de

266 8 Dressing via local Riemann–Hilbert problem

Now we deﬁne a modiﬁed Bloch function χ =˜χ exp(−iΛx − iΩt)σ

which

satisﬁes the linear equations χ

= Uχ − iΛχσ

,andχ

= Vχ− iΩχσ

and

allows the asymptotic expansion χ = χ

(0)

+ k

−1

(1)

+ O(k

−2

). Therefore, we

obtain for the plane wave potential

(k, x, t)=exp[−i(c

− ω)tσ

]

⎛

⎜

⎝

1 −

μ − Λ

⎞

⎟

⎠

× exp [i(μ − Λ)(x +2Λt)σ

]exp



i(αμc

− ω)tσ



and the leading term of the asymptotic series χ

(0)

−(i/2)αc

[x+(3/2)αc

t]σ

We see once again that this leading term is not a unit matrix, in contrast

to the NLS equation. Once again this is a manifestation of the fact that the

MNLS equation does not allow the canonical normalization of the associated

RH problem. Therefore, we perform now one more transformation of the Blo ch

solution, φ = χ

(0)−1

χ, to have the unit matrix in the asymptotic expansion:

φ = 11+k

−1

(1)

+ O(k

−2

). φ satisﬁes the linear equations

= U

′

φ − iΛφσ

,φ

= V

′

φ − iΩφσ

, (8.102)

where

′

=iΛσ

+ikQ

′

ασ

′2

, (8.103)

′

=iΩσ

+2ikΛQ

′

− ik

′2

+ kσ

′

−

′

] −

′4

Here the new potential Q

′

is related to the initial one Q as

′

= χ

(0)−1

Qχ

(0)

. (8.104)

Evidently, Q

′2

= Q

. Besides, φ

(1)

is expressed via the potential as follows:

(1)

′

8.6.3 MNLS equation: dressing of plane wave

Suppose a new solution of the linear equations (8.102) follows from the known

one φ

by dressing φ = Γφ

. As before, we take the complex double points

as the p oles of the dressing factor; therefore, we have four poles k

= k

, k

= −k

,and

= −

. Expanding the relation φ = Γφ

in the

asymptotic series gives in accordance with (8.104) and (8.103)

Q = χ

(0)

(

(0)

−1

(0)

(1)

)

(χ

(0)

)

−1

8.6 Homoclinic orbits via dressing method 267

Because φ(k =0)and(χ

(0)

)

−1

obey the same equation y

=(i/2) ασ

′

and φ(k =0)=Γ

(k =0),wegetχ

(0)

= χ

(0)

−1

,whereΓ

= Γ (k =0).

Therefore, we obtain the connection between the new and old solutions o f the

MNLS equation:

Q = Γ

−1



(0)

(1)

(0)−1



or in components

u =

(Γ

)

(Γ

)

(

exp



−iαc

x − i

)

. (8.105)

In full agreement with the results of Sect. 8.2.3 we represent the dressing

factor in the form

Γ (k)=

11 −



j,l=1

k −

|j(D

−1

)

l|,D

l|j

−

. (8.106)

Diﬀerentiating φ = Γφ

in x gives U

′

(x, k)=−Γ [ ∂

− U

′

(x, k)] Γ

−1

.From

the condition of vanishing residues at the points k

and k

we obtain the

equations

|j

= U

′

)|j, |j

= V

′

)|j,j=1, 2. (8.107)

Note that the vector |2 is related to |1 as |2 = σ

|1, in virtue of the parity

property U

′

)=U

′

(−k

)=σ

′

)σ

. Hence,

1|1

−

= −D

2|1

−

= −D

As a result, we obtain Γ

and Γ

(1)

entering (8.105) in the form

=diag



(|11|)

− D

, 1+

(|11|)

+ D



≡ diag (Γ

,Γ

(1)

= −2



0(|11|)

− D

)

−1

(|11|)

+ D

)

−1



Because D

are expressed in terms of the vector |1 [see (8.106)], we have to

obtain it explicitly. Next we wi ll account for the explicit (x, t)-dependence of

the vector |1 and justify the name “homoclinic” for the solution (8.105).

8.6.4 MNLS equation: homo clinic solution

Integrating linear equations (8.107), we obtain

|1 =exp



αc

xσ



exp

(

−i



− ω −



tσ

)

exp



(γ +iβ)





iξ− τ

−iξ +τ



−(τ +Φ)

i(ξ−λ

−

)

− e

τ +Φ

−i(ξ−λ

)



i(δ/2)



268 8 Dressing via local Riemann–Hilbert problem

Here γ and β are r eal integration constants, μ

= μ(k

)=π/L, ξ = μ

(x +

2αc

t)+(1/2)β, τ =2cμ

t − (1/2)γ,

Φ =

log

1+αμ

1 − αμ

, tan λ

(μ

/c)+(1/2) αc

, and tan δ =

αcl

1 − (1/2) α

Hence, the matrix elements are written as

=2e

(A + B)(k

−

)

−1

=2e

(A − B)(k

)

−1

where

A(ξ,τ)=cosh2τ +cos2ξ, B(ξ,τ)=cosh2(τ + Φ) − cos(2ξ − λ

− λ

−

and

A +

A + k

i(Θ−δ)

,Γ

A + k

A +

−i(Θ+δ)

tan

−

A − B

A + B

exp(−iαc

x)exp



−

iα



(1)

= −

iαl

exp(−iδ/2)

A + k



2τ

2iξ



Φ−iλ

−



−2τ

−2iξ



−Φ+iλ

−



Substituting the above formulas into (8.105), we obtain explicitly the homo-

clinic solution of the MNLS equation:

u =



1 −

2i l

−i(δ/2)

A + k

!

2τ

2iξ

Φ−iλ

−

−2τ

−2iξ

−Φ+iλ

−



−2iΘ

(8.108)

The solution (8.108) is indeed homoclinic to the plane wave b ecause

τ →±∞: u → u

exp [−2i(Θ

+ Φ

)] ,

= lim

τ →±∞

Θ = ±arctan



1 −



1 −



+(αc l

)

= ±

arctan

2cl

− c

In the α → 0 limit, if the spectral parameter k is represented as k =1−

αk

NLS

+ O(α

), the solution (8.108) reproduces the NLS homoclinic orbit

(8.101).