Doktorov E.V., Leble S.B. A Dressing Method in Mathematical Physics
Подождите немного. Документ загружается.

8.2 Nonlinear Schr¨odinger equation 229
First we intro d u ce the so-called Jost solutions J
±
(x, k) of the spectral
equation (8.8) obeying the asymptotic conditions J
±
→ 11atx →±∞.Since
tr U = 0, these boundary conditions guarantee that det J
±
=1forallx.In
other words, the Jost solutions coincide asymptotically with the solution of
the spectral equation with zero potential. It is clear now that going from the
matrix ψ to the matrix J enables us to use the unit asymptotic for J
±
,instead
of the exponential asymptotic E.
Being solutions of the first-order differential equation, the Jost functions
J
±
are not mutually independent. Indeed, they are interconnected by the
scattering matrix S(k),
J
−
= J
+
ESE
−1
,S(k)=
a(k) −
¯
b(k)
b(k)¯a(k)
, det S(k)=1, (8.9)
and the structure of S(k) is dictated by the form of the potential Q. It follows
directly from the spectral equation (8.8) that the Jost solutions obey the
involutive condition
J
†
±
(x,
¯
k)=J
−1
±
(x, k), (8.10)
where the dagger means the Hermitian conjugation. It is extremely imp or tant
that the involution (8.10) manifests itself throughout all the other objects
related to the spectral equation. For example, the scattering matrix S(k)
obeys the same involution S
†
(
¯
k)=S
−1
(k).
8.2.2 Analytic solutions
What can we say about analytic properties of the Jost matrix functions with
respect to the spectral parameter k? Let us rewrite the spectral equation (8.8)
with the boundary conditions in the integral form. To take an example, we
obtain the following integral equations
(J
−
)
11
(x, k)=1+
x
−∞
dξu(ξ)(J
−
)
21
(ξ,k),
(J
−
)
21
(x, k)=−
x
−∞
dξ ¯u(ξ)(J
−
)
11
(ξ,k)exp[2ik(x − ξ)] (8.11)
for the fir st column entries of the Jost matrix J
−
. We see that the exponent
in the integrand (8.11) decreases for Imk>0. In other words, the first column
J
[1]
−
of the matrix J
−
is analytic in the upper half plane and continuous on
the real axis Im k = 0. In the same way we recognize that the second column
J
[2]
+
of the matrix J
+
is analytic as well in the same domain. Therefore, we
can define the matrix function Φ
+
(x, k),
Φ
+
(x, k)=
!
J
[1]
−
,J
[2]
+
"
,
which is a solution of the spectral equation (8.8) and is analytic as a whole in
the upper half plane.

230 8 Dressing via local Riemann–Hilbert problem
TheanalyticsolutionΦ
+
(x, k) can be expressed in terms of the Jost func-
tions and some elements of the scattering matrix. Indeed, remembering (8.9),
we have
Φ
+
=
!
J
[1]
−
,J
[2]
+
"
=
!
aJ
[1]
+
+ b e
2ikx
J
[2]
+
,J
[2]
+
"
=
!
J
[1]
+
,J
[2]
+
"
a 0
b e
2ikx
1
= J
+
ES
+
E
−1
,
where
S
+
=
a 0
b 1
. (8.12)
Similarly,
Φ
+
= J
−
ES
−
E
−1
,S
−
=
1
¯
b
0 a
,S
+
= SS
−
. (8.13)
It follows from the above formulas that
det Φ
+
(x, k)=a(k). (8.14)
Now, what about a matrix function analytic in the lower half plane? We
can define such a function Φ
−1
−
(x, k) by means of the involution (8.10), i.e.,
Φ
−1
−
(x, k)=Φ
†
+
(x,
¯
k).
ItcanbeeasilyshownthatΦ
−1
−
(x, k) is expressed in terms of the rows of
J
−1
±
,namely,
Φ
−1
−
=
(J
−
)
−1
[1]
(J
+
)
−1
[2]
.
Therefore, Φ
−1
−
(x, k) is a solution of the adjoint spectral problem. On the real
axis
Φ
−1
−
(x, k)=Φ
†
+
(x, k)=ES
†
+
E
−1
J
−1
+
= ES
†
−
E
−1
J
−1
−
and det Φ
−1
−
(x, k)=¯a(k).
Let us write an asymptotic expansion for Φ
+
(x, k),
Φ
+
(x, k)=11+
1
k
Φ
(1)
+
(x)+O
1
k
2
, (8.15)
and substitute it into the spectral equation (8.8). Collecting terms with equal
powers of k, we find a reconstruction formula for the potential:
Q =i
σ
3
,Φ
(1)
+
. (8.16)
Hence, in order to solve the NLS equation, we should find the analytic solu-
tion Φ
+
.

8.2 Nonlinear Schr¨odinger equation 231
8.2.3 Matrix R H problem
Let us calculate a product Φ
−1
−
(x, k)Φ
+
(x, k)forImk = 0. We easily find that
this product depends essentially on k only, the x-dependence being given by
the simple exponential function E. Indeed,
Φ
−1
−
(x, k)Φ
+
(x, k)=EG
0
(k)E
−1
,G
0
= S
†
+
S
+
=
1
¯
b
b 1
(8.17)
with account for |a|
2
+ |b|
2
= 1. Hence, we arrive at the matrix RH problem!
This problem arises naturally provided we operate wi th analytic solutions of
the spectral problem. The contour L, being the real axis Im k = 0, divides
the complex k-plane into the domains C
+
,Imk>0,andC
−
,Imk<0. The
normalization of the RH problem (8.17) is canonical,
Φ
±
(x, k) −→ 11fork →∞,
owing to (8.15).
The RH problem (8.17) is characterized by the so-called RH data which
are categorized into discrete data (eigenvalues k
j
and eigenvectors |j;see
later) and continuous data [the matrix element b(k)]. Solitons correspond to
the discrete data of the RH problem with zeros of the scattering coefficients
a(k)and¯a(k). Because we showed in the preced ing subsection that the deter-
minants of the matrices Φ
+
and Φ
−1
−
are given by a(k)and¯a(k), respectively,
these matrices have zeros at the points k
j
,
¯
k
l
in their domains of analytic-
ity, i.e., det Φ
+
(k
j
)=0,Imk
j
> 0, j =1, 2,..., N, and det Φ
−1
−
(
¯
k
l
)=0,
Im
¯
k
l
< 0, l =1, 2,..., N . We suppose that all zeros are simple and of finite
number. Besides, in virtue of the involution (8.10), we have an equal number
N of zeros in both domains. The case of multiple po i nts of the RH problem
associated with the Zakharov–Shabat spectral problem has been studied by
Shchesnovich and Yang [401].
We will solve the RH problem with zeros (8.17) by means of its regular-
ization. This procedure consists in extracting rational factors from Φ
+
which
are responsible for the existence o f zeros. In fact, these rational factors rep-
resent specific Darboux transformations which produce simple zeros in the
wave function Φ
+
(Chap. 3). Indeed, if det Φ
+
(k
j
) = 0, then at the point k
j
there exists a n eigenvector |χ
j
with zero eigenvalue, Φ
+
(k
j
)|χ
j
=0.Letus
introduce a rational matrix function
Ξ
−1
j
= 11+
k
j
−
¯
k
j
k − k
j
P
j
,P
j
=
|χ
j
χ
j
|
χ
j
|χ
j
.
Here P
j
is the rank 1 projector, P
2
j
= P
j
,andχ
j
| = |χ
j
†
(cf. Chap. 3). In a
relevant basis P
j
=diag(1, 0); hence, det Ξ
−1
j
=(k −
¯
k
j
)(k − k
j
)
−1
. Because
det Φ
+
(k) ∼ (k − k
j
)nearthepointk
j
, we evidently have det(Φ
+
Ξ
−1
j
) =0
at the point k
j
. Thereby we succeeded in regularizing the RH problem at the
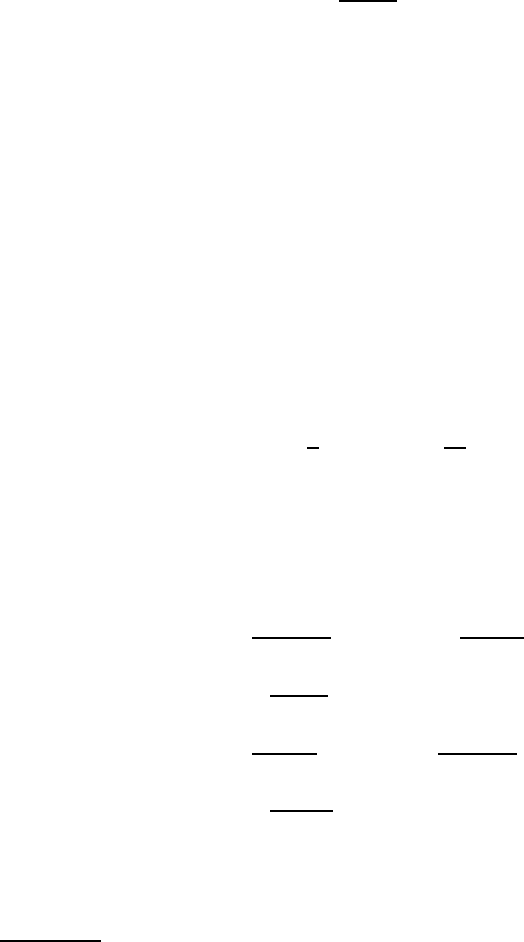
232 8 Dressing via local Riemann–Hilbert problem
point k
j
.Zero
¯
k
l
of the matrix function Φ
−1
−
is regular i zed by the rational
function
Ξ
l
= 11 −
k
l
−
¯
k
l
k −
¯
k
l
P
l
and the matrix Ξ
l
Φ
−1
−
has no zero in
¯
k
l
. The regularization of all the other
zeros is performed similarly and eventually we obtain the following represen-
tation for the analytic solutions:
Φ
±
= φ
±
Γ, Γ = Ξ
N
Ξ
N−1
···Ξ
1
, (8.18)
where the rational matrix function Γ (x, k) accumulates a ll zeros of the RH
problem, while the matrix functions φ
±
solve the regular RH problem (i.e.,
without zeros):
φ
−1
−
(x, k)φ
+
(x, k)=Γ (x, k)EG
0
(k)E
−1
Γ
−1
(x, k). (8.19)
If we restrict ourselves to obtaining the soliton solutions of the NLS equation,
i.e., for G
0
= 11, we can pose without loss of generality φ
±
= 11.
1
As a result,
Φ
+
= Γ .ThematrixΓ will be called the dressing factor. It follows from
(8.18) that the asymptotic expansion for the dressing factor is written as
Γ (x, k)=11+
1
k
Γ
(1)
(x)+O
1
k
2
. (8.20)
For practical purposes, it is more convenient to decompose the product
(8.18) into simple fractions [124, 235]. In general, the rational matrix function
Γ (k) a nd its inverse can be decomposed into terms of two sets of the vectors
|x
j
and |y
j
:
Γ (k)=
11 −
k
N
−
¯
k
N
k −
¯
k
N
P
N
···
11 −
k
1
−
¯
k
1
k −
¯
k
1
P
1
= 11 −
N
l=1
k
l
−
¯
k
l
k −
¯
k
l
|x
l
y
l
|,
Γ
−1
(k)=
11+
k
1
−
¯
k
1
k − k
1
P
1
···
11+
k
N
−
¯
k
N
k − k
N
P
N
= 11+
N
j=1
k
j
−
¯
k
j
k − k
j
|y
j
x
j
|. (8.21)
Hence, instead of N vectors |χ
j
we obtained 2N vectors |x
j
and |y
j
.
The next problem is to express |x
j
in terms of |y
j
. Consider the identity
1
In the examples in the following sections such a simple choice will not be valid.
Moreover, for the perturbed NLS equations the equality φ
±
=11 is valid in the
leading-order approximation only.
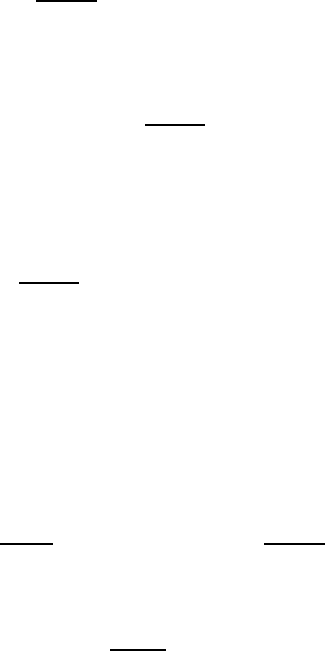
8.2 Nonlinear Schr¨odinger equation 233
Γ (k)Γ
−1
(k)=11atthepointk = k
j
. To avoid divergence at k → k
j
, we should
pose Γ (k
j
)|y
j
x
j
| =0,or
11 −
N
l=1
k
l
−
¯
k
l
k
j
−
¯
k
l
|x
l
y
l
|
|y
j
x
j
| =0.
Multiply it by |y
j
on the right. Because x
j
|y
j
=0,weobtain
|y
j
=
N
l=1
|x
l
y
l
k
l
−
¯
k
l
k
j
−
¯
k
l
y
j
. (8.22)
Let us introduce N×Nmatrices
X =(|x
1
, |x
2
,...,|x
N
),Y=(|y
1
, |y
2
,...,|y
N
),
D = {D
lj
} =
y
l
1
k
j
−
¯
k
l
y
j
0
,F= diag(...,k
l
−
¯
k
l
,...).
Then (8.22) is written as Y = XFS,orXF = YS
−1
.Incomponents,
(k
l
−
¯
k
l
)|x
l
=
N
j=1
D
−1
jl
|y
j
.
Substituting it into (8.21) and introducing more convenient notation |j≡|y
j
,
we obtain the desired formula for the dressing factor:
Γ (k)=11 −
N
j,l=1
1
k −
¯
k
l
|j
D
−1
jl
l|,D
lj
=
l|j
k
j
−
¯
k
l
. (8.23)
Similarly,
Γ
−1
(k)=11+
N
j,l=1
1
k − k
j
|j
D
−1
jl
l|. (8.24)
Let us remember the reconstruction formula (8.16), which is now written
as
Q =i
σ
3
,Γ
(1)
(x)
. (8.25)
As a result, we will be able to find solutions o f the NLS equation, provided
we can calculate explicitly th e matrix Γ or, more precisely, the vector |j.To
this end, l et us differentiate the equation Φ
+
(k
j
)|j =0inx. Because Φ
+
is a
solution of the spectral equation (8.8), we obtain
∂
x
Φ
+
(x, k)
k
j
|j + Φ
+
(x, k
j
)|j
x
=ik
j
Φ
+
(x, k
j
)σ
3
|j+ Φ
+
(x, k
j
)|j
x
=0.
Therefore, the x-dependence of |j is given by a simple linear equation
|j
x
= −ik
j
σ
3
|j. (8.26)
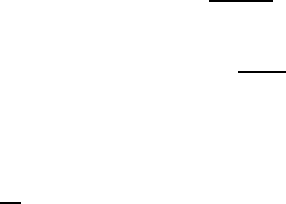
234 8 Dressing via local Riemann–Hilbert problem
In the same manner we find the evolutionary equation
|j
t
= −2ik
2
j
σ
3
|j. (8.27)
Integrating them, we obtain explicitly the vector |j as
|j =exp
(−ik
j
x − 2ik
2
j
t)σ
3
|j
0
, (8.28)
where |j
0
is a vector integration constant.
8.2.4 Soliton solution
With the above results in hand, we can now derive the soliton solution of the
NLS equation. We have in this case N = 1 and pose k
1
= ξ +iη. Then the
vector |1 (8.28) takes the form
|1 =
exp
&
η(x +4ξt) − i
ξx +2(ξ
2
− η
2
)t
'
p
1
exp
&
−η(x +4ξt)+i
ξx +2(ξ
2
− η
2
)t
'
p
2
,
where p
1
and p
2
are components of the constant vector |1
0
. The reconstruc-
tion formula (8.25) reduces to
u(x, t)=2iΓ
(1)
12
(x, t). (8.29)
It follows from
Γ = 11 −
k
1
−
¯
k
1
k −
¯
k
1
P
1
that
Γ
(1)
= −2iη
|11|
1|1
. (8.30)
It is important that the vector |1 enters (8.30) bo th in the numerator and in
the denominator. Therefore, we can divide b oth components of the vector by
the same number, say p
2
, without changing Γ
(1)
.Denoting
e
a+iβ
=
p
1
p
2
,z=2η(x +4ξt)+a, ϕ = −2ξx − 4(ξ
2
− η
2
)t + β,
we can r epresent the vector |1 in the very simple form:
|1 =e
(1/2)(a+iβ)
e
(1/2)(z+iϕ)
e
−(1/2)(z+iϕ)
. (8.31)
Substituting this v e c tor into (8.30), we find
Γ
(1)
= −iη
e
z
e
iϕ
e
−iϕ
e
−z
sechz
and, in accordance with (8.29), we finally obtain the standard formula [473]
for the NLS soliton:
u(x, t)=2ηe
iϕ
sechz. (8.32)
Here ξ and η determine the soliton velocity and amplitude, resp ectively, whi le
a and β give the initial position and phase of the soliton.

8.2 Nonlinear Schr¨odinger equation 235
8.2.5 NLS breather
In this subsection we will obtain the breather solution of the NLS equa-
tion. The breather is an oscillating “bound state” of two solitons centered
at the same p osition and having equal velo cities. Without loss of general-
ity, we take the velocity of the solitons to be zero (ξ
1
= ξ
2
=0).Asa
result,wehavenowfourzerosofthe RH problem, two of them lying on
the positive imaginary axis, k
1
=iη
1
and k
2
=iη
2
, and the other two
zeros lying on the negative imaginary axis,
¯
k
1
= −iη
1
and
¯
k
2
= −iη
2
.
Therefore, the dressing factor Γ entering the reconstruction formula (8.25)
is written in the form (8.23) for N = 2 and gives after the asymptotic
expansion
Γ
(1)
= −
2
j,l=1
|j(D
−1)
)
jl
l| (8.33)
= −(D
−1
)
11
|11|−(D
−1
)
21
|21|−(D
−1
)
12
|12|−(D
−1
)
22
|22|.
The matrix elements D
lj
are given by (8.23) and hence the matrix D takes
the form
D =
⎛
⎜
⎝
1|1
k
1
−
¯
k
1
1|2
k
2
−
¯
k
1
2|1
k
1
−
¯
k
2
2|2
k
2
−
¯
k
2
⎞
⎟
⎠
.
We can rewrite (8.33) immediately in terms of the matrix D:
Γ
(1)
=(detD)
−1
[−D
22
|11| + D
21
|21| + D
12
|12|−D
11
|22|]. (8.34)
The vector |j, j =1, 2, has the form [see (8.31)]
|j =e
(i/2)β
j
e
(1/2)(z
j
+iϕ
j
)
e
−(1/2)(z
j
+iϕ
j
)
,z
j
=2η
j
x, ϕ
j
=4η
2
j
t + β
j
,
and we put a
j
= 0 because the maxima of both solitons coincide. Let us first
calculate matrix elements D
lj
:
D
12
=
e
−(i/2)(β
1
−β
2
)
i(η
1
+ η
2
)
exp
1
2
(z
1
+ z
2
− iϕ
1
+iϕ
2
)+exp
1
2
(−z
1
− z
2
+iϕ
1
− iϕ
2
)
,
D
21
= −D
∗
12
,D
11
=
cosh z
1
iη
1
,D
22
=
cosh z
2
iη
2
.
Then we obtain the determinant of D:
det D =
2
(η
1
+ η
2
)
2
cosh(z
1
+ z
2
)+cos(ϕ
1
− ϕ
2
) −
(η
1
+ η
2
)
2
2η
1
η
2
cosh z
1
cosh z
2
.

236 8 Dressing via local Riemann–Hilbert problem
Remember that the two-soliton solution is given by (8.29). Calculating now
Γ
(1)
12
by means of (8.32)–(8.34), we find
Γ
(1)
12
=
1
idetD
η
1
− η
2
η
1
+ η
2
cosh z
1
η
1
e
iϕ
2
−
cosh z
2
η
2
e
iϕ
1
.
Hence,
u(x, t)=(η
2
1
− η
2
2
)
cosh 2η
1
x
η
1
exp
4iη
2
2
t +iβ
2
−
cosh 2η
2
x
η
2
exp
4iη
2
1
+iβ
1
×
cosh 2(η
1
+ η
2
)x +cos
4(η
2
1
− η
2
2
)t + β
1
− β
2
(8.35)
−
(η
1
+ η
2
)
2
2η
1
η
2
cosh 2η
1
x cosh 2η
2
x
−1
.
This formula describes the two-soliton solution of the NLS equation but it is
not yet a breather. The breather being a result of the evolution of the initial
configuration u(x, 0) = 2 sech x is obtained under definite relations between
η
1
and η
2
and between β
1
and β
2
[387]. Considering u(x, t) (8.35) for t =0,
we easily find that we should take η
1
=3/2, η
2
=1/2, β
1
=0,andβ
2
= π.
As a result, the breather solution of the NLS equation is written as
u(x, t)=4e
it
cosh 3x +3e
8it
cosh x
cosh 4x +4cosh2x +3cos8t
. (8.36)
The breather (8.36) oscillates with the frequency ω =8.
In conclusion, let us summarize the basic steps in the derivation of the
soliton solution. First we built analytic solutions of the spectral problem from
the components of the Jost solutions. Then we showed that the analytic solu-
tions solve the RH problem with zeros. After regularization of the RH problem
we extracted the rational dressing factor. The dressing factor is determined
by the discrete RH data, i.e., eigenvalues and eigenvectors. The eigenvalues
are constants of motion, while the eigenvectors are governed by simple linear
equations. After integrating these equations we obtained the eigenvectors ex-
plicitly that enable us to calculate the dressing factor and finally to derive the
soliton solution.
8.3 Modified nonlinear Schr¨odinger equation
In this section we will obtain soliton solutions of the MNLS equation taking
as a seed solution the trivial one u = 0. The MNLS equation
iu
t
+ u
xx
+2|u|
2
u +iα
|u|
2
u
x
=0,α∈ Re (8.37)
for a scalar complex function u(x, t) has important applications in nonlinear
optics [23, 121, 180, 432, 442] and plasma physics [213, 334]. In particular,
this equation extends the famous NLS equation to the case of subpicosecond
optical pulses. For definiteness we take hereafter the parameter α>0.

8.3 Modified nonlinear Schr¨odinger equation 237
8.3.1 Jost solutions
Equation (8.37) allows the Lax representation (8.2) with the matrices U and
V of the form
U = −
i
α
(k
2
− 1)σ
3
+ikQ, Q =
0 u
¯u 0
, (8.38)
V = −
2i
α
2
(k
2
− 1)
2
σ
3
+
2i
α
k(k
2
− 1)Q +ik
2
Q
2
σ
3
− kσ
3
Q
x
− iαkQ
3
.
As for the NLS equation, we define a matrix J = ψE
−1
,where
E =exp
−(i/α)(k
2
− 1)xσ
3
is a solution of the equation ψ
x
= Uψ for zero potential Q = 0; hence, a
spectral equation for the MNLS equation is written as
J
x
= −
i
α
(k
2
− 1) [σ
3
,J]+ikQJ. (8.39)
This spectral problem, being quadratic in the spectral parameter k, belongs
to the Wadati–Konno–Ichikawa (WKI) class [444]. The Hamiltonian structure
and squared solutions of equations solvable by the quadratic spectral problem
have been studied by Gerdjikov and Ivanov [183, 184]. It should be noted that
the MNLS equation can b e transformed by a gauge transformation [330] to
the so-called derivative NLS equation [233] which i s also applicable in plasma
physics [119, 337, 411].
Jost solutions J
±
(x, k)of(8.39) are determined by the asymptotics J
±
→ 11
as x →±∞and det J
±
= 1. The scattering matrix S(k)isgivenbythe
equations of the form (8.9) for Im k
2
= 0 and the involution (8.10) preserves
its form for the MNLS Jost functions a s well.
There exists another symmetry of the sp ectral equation (8.39). Indeed, it
can be easily shown that a solution of the spectral equation satisfies a parity
condition
J(k)=σ
3
J(−k)σ
3
. (8.40)
This condition means that the diagonal entries of the matrix J are even func-
tions of k, while off-diagonal ones are odd functions. Evidently, the parity con-
dition (8.40) is valid as well for the scattering matrix. In particular, we find
that the scattering matrix elements obey the parity conditions a(k)=a(−k)
and b(k)=−b(−k).
Let us consider now the asymptotic expansion of the Jost solutions at
k →∞,
J
±
(x, k)=J
(0)
±
(x)+
1
k
J
(1)
±
(x)+O
1
k
2
. (8.41)
As a consequence of the parity property (8.40), the expansion coefficients
J
(2n)
±
, n =0, 1,..., are diagonal matrices, while J
(2n+1)
±
, n =0, 1,...,are

238 8 Dressing via local Riemann–Hilbert problem
off-diagonal matrices. Substituting the series (8.41) into the spectral equation,
we find the l eading-order terms J
(0)
±
(x)as
J
(0)
±
(x)=exp
−
iα
2
σ
3
x
±∞
|u(ξ)|
2
dξ
.
Hence, we arrive at the important conclusion that the asymptotic expansion
with the unit matrix as the leading-order term, like for the NLS equation, is
incompatible with the sp ectral equation (8.39).
8.3.2 Analytic solutions
Rewriting equatio ns for the first column of J
−
in the integral form,
J
−11
=1+ik
x
−∞
dξu(ξ) J
−21
(ξ),
J
−21
=ik
x
−∞
dξ ¯u(ξ) J
−11
(ξ)exp
2i
α
(k
2
− 1)(x −ξ)
, (8.42)
we see that the exponent in the integrand of ( 8.42) decreases for Im k
2
> 0,
i.e., for k lying in the first and third quadrants of the k-plane. We denote
this domain by C
+
. In other words, the first column J
[1]
−
is analytic in C
+
and sectionally continuous on Im k
2
= 0, i.e., on the r eal and imaginary axes,
reaching them from C
+
. Similarly we reveal analyticity of the column J
[2]
+
in
the same domain. Therefore, a matrix function
Φ
+
=
!
J
[1]
−
,J
[2]
+
"
solves the spectral equation (8.39) and is analytic in C
+
. Similarly to the
NLS equation, we can express the analytic solution Φ
+
in terms of the Jost
functions:
Φ
+
= J
+
ES
+
E
−1
= J
−
ES
−
E
−1
,
with the same matrices S
±
as in (8.12) and (8.13). The asymptotic expansion
for Φ
+
takes the form
Φ
+
(x, k)=Φ
(0)
+
(x)+
1
k
Φ
(1)
+
(x)+O
1
k
2
. (8.43)
Substituting this expansion into the spectral equation and equating terms
with equal powers of k, we find
Φ
(1)
+
=
α
2
σ
3
QΦ
(0)
+
,Φ
(0)
+x
=iQΦ
(1)
+
.
Combining these r elations, we get two important results: first, the equation
for Φ
(0)
+
,
Φ
(0)
+x
= −
iα
2
σ
3
Q
2
Φ
(0)
+
, (8.44)
