Desurvire E. Classical and Quantum Information Theory: An Introduction for the Telecom Scientist
Подождите немного. Документ загружается.

18.7 Exercises 377
18.3 (B): Show that a Bell measurement of any of the Bell states |β
mm
outputs the
two classical bits m, m
.
18.4 (B): Given the EPR–Bell states |β
00
, |β
01
, |β
10
, |β
11
and the Pauli operators
X, Y, Z acting on the first qubit, show the following identities used for superdense
coding:
X|β
00
=|β
01
iY|β
00
=|β
11
Z|β
00
=|β
10
.
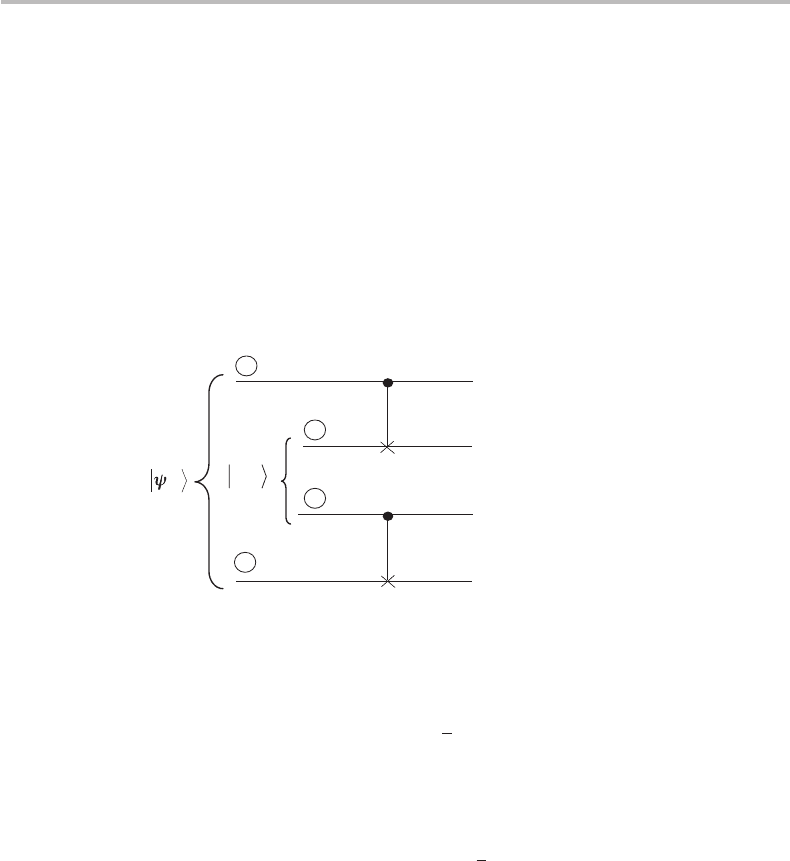
18.5 (T): Given the 4-qubit circuit
1414
1
C
12
C
34
b
00
2
3
4
with |ψ
ij
as the input qubit pairs labeled with |ψ
23
≡|β
00
(EPR–Bell state),
show that the following equality holds:
C
34
C
12
(|ψ
14
⊗|β
00
) =
1
2
|0+ ⊗ Z
0
X
0
C
14
|ψ
14
+|0− ⊗ Z
1
X
0
C
14
|ψ
14
+|1+ ⊗ Z
0
X
1
C
14
|ψ
14
−|1− ⊗ Z
1
X
1
C
14
|ψ
14
,
where
(i) |0+, |0−, 1+, |1− are tensor products of the |0, |1 states with the
|+, |− states (|± = (|0±|1)/
√
2);
(ii) X, Z are the usual Pauli matrices, used here to the powers 0 or 1, and applying
on qubit 1 for Z and qubit 4 for X ;
(iii) C
ij
is the CNOT gate for the 2-qubit |ψ
ij
, with i as the control qubit and j
as the target qubit.

19 Deutsch–Jozsa, quantum Fourier
transform, and Grover quantum
database search algorithms
This mathematically intensive chapter takes us through our first steps in the domain of
quantum computation (QC) algorithms. The simplest of them is the Deutsch algorithm,
which makes it possible to determine whether or not a Boolean function is constant
for any input. The key result is that this QC algorithm provides the answer at once,
whereas in the classical case it would take two independent calculations. I describe next
the generalization of the former algorithm to n qubits, referred to as the Deutsch–Jozsa
algorithm. Although they have no specific or useful applications in quantum computing,
both algorithms represent a most elegant means of introducing the concept of quantum
computation parallelism. I then describe two most important QC algorithms, which
nicely exploit quantum parallelism. The first is the quantum Fourier transform (QFT),
for which a detailed analysis of QFT circuits and quantum-gate requirements is also
provided. As will be shown in the next chapter, a key application of QFT concerns the
famous Shor’s algorithm, which makes it possible to factor numbers into primes in terms
of polynomials. The second algorithm, no less famous than Shor’s, is referred to as the
Grover quantum database search, whose application is the identification of database
items with a quadratic gain in speed.
19.1 Deutsch algorithm
Our exploration of quantum algorithms shall begin with the solution of a very basic
problem: finding whether or not a Boolean function f (x) is a constant. The solution is
given by the Deutsch algorithm, which illustrates a fundamental property of quantum
computing, namely parallelism. As we shall indeed see, quantum computation makes
it possible to evaluate f (x) simultaneously for all values of the variable x, in contrast
to classical computing (i.e., von Neumann architecture, Chapter 15) where such an
evaluation must be performed one variable at a time, or through as many computers
working in parallel.
Assume then a Boolean function f (x) where x is a binary variable. We can con-
ceive of a 2-qubit quantum circuit based on a unitary operator U
f
that achieves the
transformation
U
f
|x, y=|x, y ⊕ f (x), (19.1)
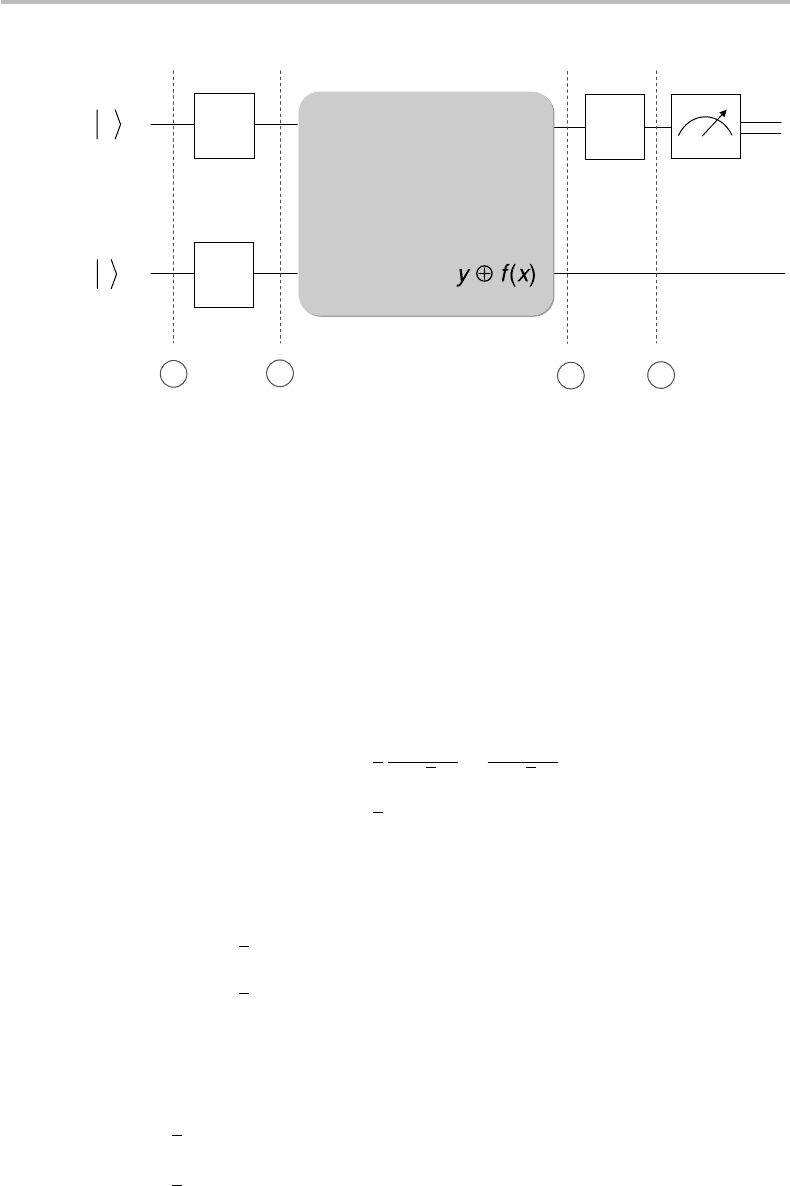
19.1 Deutsch algorithm 379
H
0
1
H
H
x
y
x
f
U
1
2
3
4
Figure 19.1 Quantum circuit for implementing the Deutsch algorithm.
where the simplified notation |u,v=|u⊗|vstands for tensor product. Consider next
the quantum circuit arrangement shown in Fig. 19.1, where H are Hadamard gates and
|0, |1 are two ancilla qubits. We call x, y the inputs resulting from the Hadamard
transforms on the two ancilla qubits, and note that the action of the “black box” gate U
f
on x, y results in the outputs x, y ⊕ f (x). Let us now analyze the evolution of the tensor
state, from left to right, through the locations marked ➀➁➂➃ in the figure, starting from
|ψ
1
=|01=|0⊗|1 at ➀:
➁ :
|
ψ
2
= H
1
H
2
|
ψ
1
= H
1
|0⊗H
2
|1
=
|
+
⊗
|
−
=
1
2
|0+|1
√
2
⊗
|0−|1
√
2
=
1
4
(
|
00
−
|
01
+
|
10
−
|
11
)
(19.2)
(note the factor
1
/
2
introduced in the right-hand side, to ensure normalization of the tensor
product of mixed states). Then, using the definition in Eq. (19.1):
➂ : U
f
|
ψ
2
=
1
4
U
f
(
|
00
−
|
01
+
|
10
−
|
11
)
≡
1
4
(
|
0, 0 ⊕ f (0)
−
|
0, 1 ⊕ f (0)
+
|
1, 0 ⊕ f (1)
−
|
1, 1 ⊕ f (1)
)
.
(19.3)
Then, ➃:
|
ψ
3
= H
1
|
ψ
2
=
1
4
H
1
(
|
0, 0 ⊕ f (0)
−
|
0, 1 ⊕ f (0)
+
|
1, 0 ⊕ f (1)
−
|
1, 1 ⊕ f (1)
)
=
1
4
(
|
+, 0 ⊕ f (0)
−
|
+, 1 ⊕ f (0)
+
|
−, 0 ⊕ f (1)
−
|
−, 1 ⊕ f (1)
)
380 Quantum database search algorithms
=
1
4
√
2
(
|
0, 0 ⊕ f (0)
+
|
1, 0 ⊕ f (0)
−
|
0, 1 ⊕ f (0)
−
|
1, 1 ⊕ f (0)
+
|
0, 0 ⊕ f (1)
−
|
1, 0 ⊕ f (1)
−
|
0, 1 ⊕ f (1)
+
|
1, 1 ⊕ f (1)
)
=
1
4
√
2
{
|0
(
|
0 ⊕ f (0)
+
|
0 ⊕ f (1)
−
|
1 ⊕ f (0)
−
|
1 ⊕ f (1)
)
(19.4)
+|1
(
|
0 ⊕ f (0)
−
|
0 ⊕ f (1)
−
|
1 ⊕ f (0)
+
|
1 ⊕ f (1)
)
}
≡
1
2
√
2
|0
|
f (0)
+
|
f (1)
2
−
|
1 ⊕ f (0)
+
|
1 ⊕ f (1)
2
+|1
|
f (0)
−
|
f (1)
2
−
|
1 ⊕ f (0)
−
|
1 ⊕ f (1)
2
%
.
Next consider the two cases (a) a = f (0) = f (1), and (b) a = f (0) = f (1) =
¯
a.From
Eq. (19.4), we obtain:
|
ψ
3
f (0)= f (1)
=
1
2
√
2
|0
|
a
+
|
a
2
−
|
1 ⊕ a
+
|
1 ⊕ a
2
+|1
|a−|a
2
−
|
¯
a−|
¯
a
2
%
=
|0
(
|
a
−
|
¯
a
)
2
√
2
|
ψ
3
f (0)= f (1)
=
1
2
√
2
|0
|
a
+
|
¯
a
2
−
|
¯
a
+
|
a
2
+|1
|
a
−
|
¯
a
2
−
|
¯
a
−
|
a
2
%
=
|1
(
|
a
−
|
¯
a
)
2
√
2
. (19.5)
Finally, we note that f (0) ⊕ f (1) = 0if f (0) = f (1) and f (0) ⊕ f (1) = 1if f (0) =
f (1). Using this property, and the definition of a Boolean variable
|
a
−
|
¯
a
=
±
(
|0−|1
)
, we obtain from Eq. (19.5) within an unobservable phase e
i
π
=−1:
|
ψ
3
≡
|
f (0) ⊕ f (1)
|0−|1
√
2
. (19.6)
The result shows that measuring the first qubit, namely,
|
f (0) ⊕ f (1)
, provides the
answer “at once” to Deutsch’s problem. Indeed, if we measure
|
f (0) ⊕ f (1)
=|0,we
conclude that f (0) = f (1) and, therefore, that f (x) is a constant, and if we measure
|
f (0) ⊕ f (1)
=|1, we conclude the opposite. Thus, Deutsch’s algorithm makes it
possible to solve the problem without having to compute f (0), f (1) separately, unlike in
the classical case. This simple problem magnifies the property of quantum parallelism,
which is the key to quantum computing.
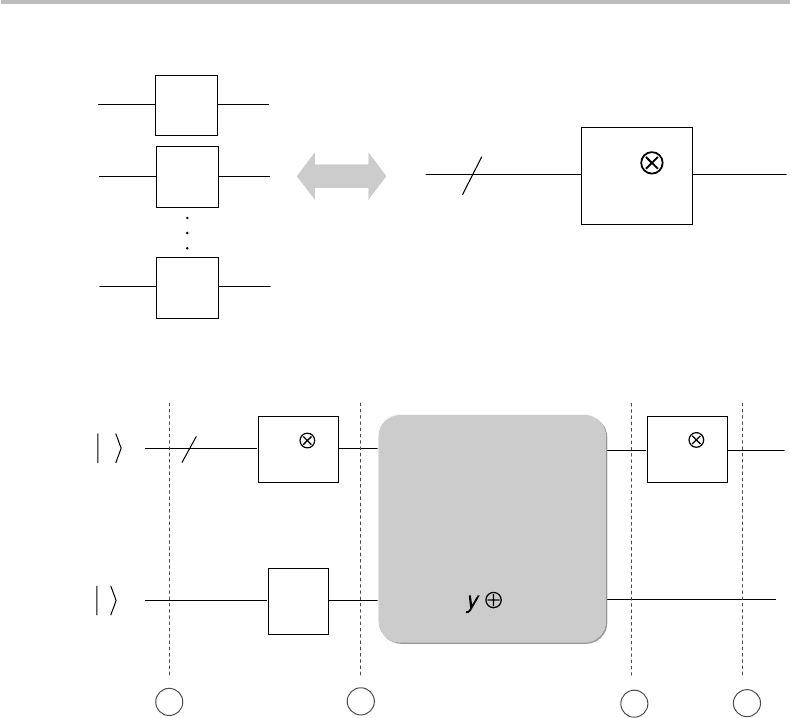
19.2 Deutsch–Jozsa algorithm 381
n
H
n
H
H
H
1
2
n
Figure 19.2 Equivalent representation for n-qubit wires, with H gates deployed in parallel.
0
1
H
x
y
f
(
x
)
x
f
U
1
2
3
4
n
H
n
n
H
Figure 19.3 Quantum circuit for implementing the Deutsch–Jozsa algorithm.
19.2 Deutsch–Jozsa algorithm
In this section, we consider the generalization of Deutsch’s algorithm, which is
referred to as the Deutsch–Jozsa algorithm. Now f (x) is a function of any inte-
ger x ∈{0, 1, 2 ...2
n−1
}, which outputs a Boolean f (x) ∈
{
0, 1
}
. What is known as
Deutsch’s problem is to find a way to tell, for all possible values of x, whether f (x)
is constant, or f (x)isbalanced, meaning in this last case that the output is 0 or 1 for
exactly one half of the possible inputs. The answer to Deutsch’s problem takes the form
of a quantum algorithm, whose circuit is similar to the previous one. The difference is
that x is not a single Boolean but a binary number, which we shall distribute over as
many qubits. As a new convention for quantum circuits, we shall represent n-qubit wires
with H gates deployed in parallel, according to Fig. 19.2. The Deutsch–Jozsa circuit
is represented in Fig. 19.3 (recalling from Chapter 17 the notation A
⊗n
for n-tensored
operators A). The circuit is seen to have n ancilla qubits |0 and one ancilla qubit |1
as inputs, which pass together through n + 1 parallel Hadamard gates. The input tensor
state at ➀ is
|
ψ
1
=
(
|0⊗|0...⊗|0
)
n times
⊗|1≡|0
⊗n
⊗|1.At➁ in Fig. 19.3,
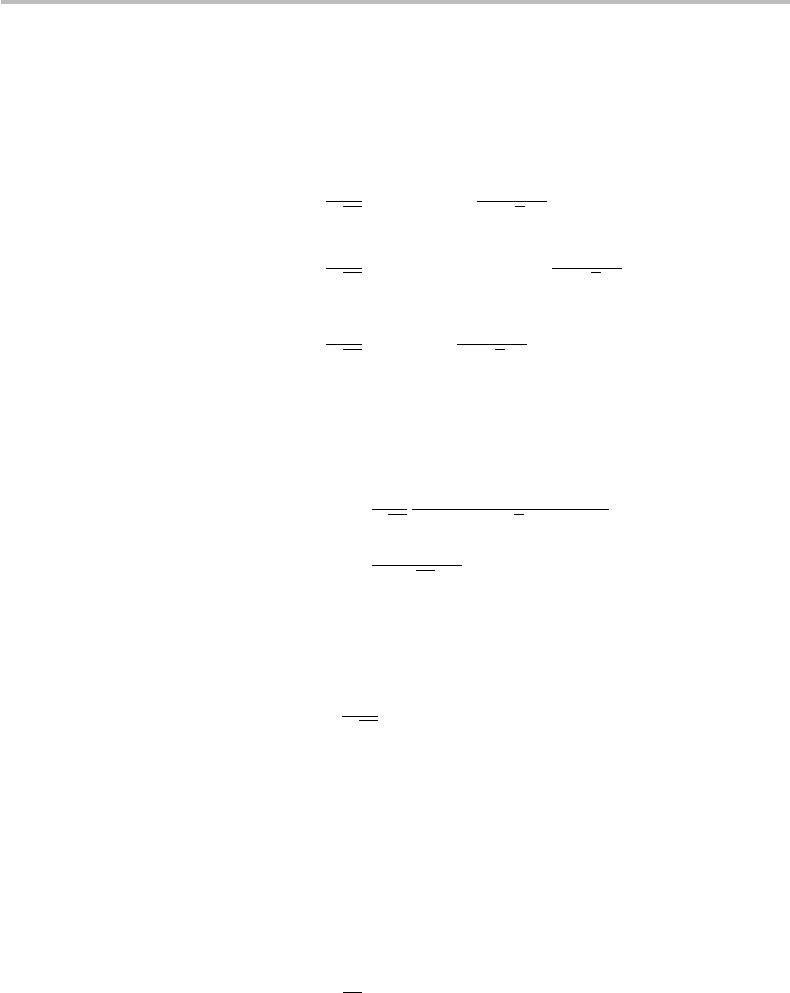
382 Quantum database search algorithms
we obtain
1
|ψ
2
=H
⊗n
H
2
|ψ
1
= H
⊗n
|0
⊗n
⊗ H |1
=
|
+
⊗n
|
−
=
1
√
2
n
(
|0+|1
)
⊗n
|0−|1
√
2
=
1
√
2
n
x
i
∈
{
0,1
}
|
x
1
x
2
...x
n
|0−|1
√
2
=
1
√
2
n
&
2
n
−1
x=0
|x
'
|0−|1
√
2
.
(19.7)
We call |xthe query register, similarly to the “register” in the classical von Neumann
architecture (Chapter 15) the difference being that it is made of qubits.At➂, we obtain
2
|
ψ
3
= U
f
|
ψ
2
=
x
|x
√
2
n
|
0 ⊕ f (x)
−
|
1 ⊕ f (x)
√
2
≡
x
(−1)
f (x)
|x
√
2
n
|
−
.
(19.8)
And at ➃, after passing the top n-qubit through the parallel gate H
⊗n
, we obtain:
|
ψ
4
= H
⊗n
|
ψ
3
=
1
√
2
n
&
x
(−1)
f (x)
H
⊗n
|x
'
|
−
.
(19.9)
To develop the right-hand side in Eq. (19.9), we must calculate H
⊗n
|x=
H
⊗n
|
x
1
x
2
...x
n
. It is an easy exercise to establish that:
H
⊗n
|x=
z
(−1)
x·z
|
z
, (19.10)
where x · z = x
1
z
1
+ x
2
z
2
+···+x
n
z
n
is a scalar product modulo 2. Combining
Eqs. (19.9) and (19.10), we then obtain:
|
ψ
4
=
1
2
n
&
z
x
(−1)
f (x)+x·z
|
z
'
|
−
≡
|
|
−
,
(19.11)
1
In the last two equations, I have introduced the equivalent n-qubit notations
x
|x =
x
i
|
x
1
x
2
...x
n
=
(
|0+|1
)
⊗n
with x
i
= 0, 1andx = 0, 1, 2 ...2
n−1
. The correspondence is easily checked with n = 2and
then by induction.
2
The last equality in Eq. (19.8) is straightforward: given x,if f (x) = 0then
|
0 ⊕ f (x)
−
|
1 ⊕ f (x)
=|0−
|1≡
(
−1
)
0
(
|0−|1
)
;if f (x) = 1then
|
0 ⊕ f (x)
−
|
1 ⊕ f (x)
= 1 −|0≡
(
−1
)
1
(
|0−|1
)
; hence,
|
0 ⊕ f (x)
−
|
1 ⊕ f (x)
≡
(
−1
)
f (x)
(
|0−|1
)
≡
(
−1
)
f (x)
|
−
in the general case.

19.3 Quantum Fourier transform algorithm 383
with
|
=
1
2
n
z
u
xz
|
z
, (19.12)
u
xz
=
x
(−1)
f (x)+x·z
. (19.13)
The n-qubit
|
defined in Eqs. (19.11) and (19.12) represents the output query
register. As we shall see, the corresponding amplitudes u
xz
contain all the information
needed to answer Deutsch’s problem. To show this, consider the two cases of interest:
f (x) is constant, or f (x) is balanced. If f (x) = a (a =±1 being a constant), all the
amplitudes u
xz
of
|
z
=|0
⊗n
are equal to u
x0
= (−1)
f (x)
= (−1)
a
=±1. Since
|
has a length of unity, this means that all other amplitudes u
x,z=0
must be zero. The
query registers thus displays
|
=|0
⊗n
, i.e., all output qubits are equal to |0. A single
measurement by projecting the register over |0
⊗n
, yielding |
⊗n
= 1, suffices to
prove the point. Consider next the second case: if f (x) is balanced, this means that the
amplitude u
x0
of
|
z
=|0
⊗n
is zero, as the terms (−1)
f (x)+x·0
= (−1)
f (x)
in the sum in
Eq. (19.3) cancel each other (one half yielding +1, the other half yielding −1). For any
x we thus have the property
x
(−1)
f (x)
= 0, indicating that f (x) is, indeed, balanced.
In this case, the query register cannot output
|
=|0
⊗n
, meaning that at least one of
the register qubits must be |1. A single projection test yielding
|
0
⊗n
= 0 suffices
to prove the point.
In summary, the Deutsch–Jozsa algorithm demonstrates the capability of quantum
parallelism over an arbitrary number of qubits n.Ittakesasingle calculation and a single
measurement of the output register
|
to obtain the answer to Deutsch’s problem. In
contrast, a classical computation would require at least “2
n
/2 plus one” measurements
with random inputs to obtain the same answer within reasonable confidence, and 2
n
measurements for absolute confidence.
While this discussion makes a point about the power of quantum parallelism,it
should not be concluded that evaluating the properties of the function f (x)isofany
particular interest to quantum computing algorithms. Rather, the Deutsch and Deutsch–
Jozsa algorithms must be regarded as representing a most elegant introduction to the
concept.
19.3 Quantum Fourier transform algorithm
In this section, I shall describe the quantum Fourier transform (QFT), which lies at
the root of several important quantum-computing algorithms, for some revolutionary
applications to be developed in Chapter 20. To avoid any misconception, QFT was not
developed with the purpose of boosting the speed of Fourier transforms, as they can
be implemented with classical bits in a von Neumann computer through the so-called
fast Fourier transform (FFT) algorithm. Rather, QFT opens up some new perspectives
in quantum computation, and we may realize this only through the next chapter. Here,

384 Quantum database search algorithms
I shall outline the formal concept and show how QFT can be practically implemented
through relatively simple circuits based on 2 × 2 and controlled 2 × 2 quantum-gates.
Let us begin by recalling the definition of the Fourier transform, as it applies to
a discrete function or N -vector. In elementary calculus, and electrical and telecom
engineering, the discrete Fourier transform (DFT)ofanN -vector x =
(
x
0
, x
1
...x
N −1
)
with complex coefficients x
k
is a well known operation. It results in the generation of N
Fourier components, y
n
(k = 0, 1 ...N − 1), as defined by the linear expansion:
3
y
n
=
1
√
N
N −1
k=0
x
k
e
i
k
2nπ
N
. (19.14)
It is seen that for each index k the terms contributing to the series expansion in
Eq. (19.14) involve powers of the discrete frequency (or tone) f
n
= 2nπ/N , which
range from f
0
= 0to f
N −1
= 2π(N − 1)/N . Thus, y
n
is the complex amplitude of
the Fourier component at frequency f
n
, the ensemble of which forms the frequency
spectrum of x. Similarly, the inverse discrete Fourier transform (IDFT) is defined as:
x
k
=
1
√
N
N −1
k=0
y
n
e
−
i
n
2kπ
N
. (19.15)
From this background, we can now introduce the quantum Fourier transform (QFT) of
an orthonormal basis
{
|k
}
k=0...N −1
≡
{
|0, |1...|N − 1
}
. Such a transform is enabled
by a unitary operator, which we call QFT, and which acts on the N basis states |k in a
way exactly similar to that in Eq. (19.14):
QFT
|
n
=
1
√
N
N −1
k=0
e
i
k
2nπ
N
|k. (19.16)
It is left as a nontrivial, but elementary exercise to show that the QFT transformation is,
indeed, unitary. Next, let
|
ψ
be a qubit of dimension N with coordinates x
k
in the basis
{
|k
}
, i.e.,
|
ψ
=
N −1
k=0
x
k
|k. (19.17)
The quantum Fourier transform of the qubit
|
ψ
, which we note |
˜
ψ, is defined as:
|
˜
ψ=QFT
|
ψ
≡
1
√
N
N −1
n=0
N −1
k=0
x
k
e
i
k
2nπ
N
|k.
(19.18)
This result establishes the formal correspondence between |
˜
ψ and |ψ.Theinverse
QFT, noted QFT
+
, is similarly defined through Eq. (19.15), which gives:
|ψ=QFT
+
|
˜
ψ
≡
1
√
N
N −1
k=0
N −1
n=0
y
n
e
−
i
n
2kπ
N
|
n
.
(19.19)
3
See, for instance, http://en.wikipedia.org/wiki/Discrete_Fourier_transform.
19.3 Quantum Fourier transform algorithm 385
As a matter of fact, the QFT is far simpler than the above formulas make it appear. Let
us show this by considering the elementary cases N = 2 and N = 3. Applying the QFT
definition for the basis transformation, we obtain in the first case:
|
y
n
=
1
√
2
1
k=0
e
i
k
2nπ
2
|
x
k
=
1
√
2
|0+
e
i
kπ
|1
,
(19.20)
hence:
|
y
0
=
1
√
2
(
|0+|1
)
≡
|
+
|
y
1
=
1
√
2
(
|0+
e
i
π
|1
)
=
1
√
2
(
|0−|1
)
≡
|
−
.
(19.21)
This result indicates that in the case N = 2, the QFT reduces to the Hadamard transfor-
mation with quantum matrix gate H . In the case N = 3, we obtain:
|
y
n
=
1
√
3
2
k=0
e
i
k
2nπ
3
|
x
k
=
1
√
3
#
|0+
e
i
2nπ
3
|1+
e
i
4nπ
3
|2
$
,
(19.22)
hence:
|
y
0
=
1
√
3
(
|0+|1+|2
)
|
y
1
=
1
√
3
#
|0+
e
i
2π
3
|1+
e
i
4π
3
|2
$
|
y
2
=
1
√
3
#
|0+
e
i
4π
3
|1+
e
i
8π
3
|2
$
.
(19.23)
We may represent the above results through a symmetric matrix M with coef-
ficients M
nk
= M
kn
= exp(
i
2nkπ/N)/
√
N ≡ ω
nk
/
√
N , where ω = exp(2
i
π/N ) and
n, k = 0 ...N − 1. The N = 3 matrix, thus, takes the form:
M =
1
√
3
11 1
1 ωω
2
1 ω
2
ω
4
. (19.24)
It is clear that, in general, the matrix M takes the following form, referred to as the
Vandermonde matrix:
M =
1
√
N
11 1 ··· 1
1 ωω
2
··· ω
N −1
1 ω
2
ω
4
··· ω
2(N −1)
1 ω
3
ω
6
··· ω
3(N −1)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
1 ω
N −1
ω
2(N −1)
··· ω
(N −1)(N −1)
. (19.25)
386 Quantum database search algorithms
1
n
2
n
3
n
1−
K
n
K
n
1
2
3
K
− 1
K
1
2
3
1−
K
K
2−
K
n
H
H
2
R
H
2
R
3
R
H
2
R
3
R
K
R
K
−1
R
K
− 2
Figure 19.4 Quantum circuit for QFT implementation.
Substituting the Vandermonde matrix into the definitions in Eqs. (19.18) and (19.19) we
also obtain the general definition of the QFT, QFT
+
qubit transformations:
|
˜
ψ=QFT
|
ψ
=
N −1
k=0
N −1
n=0
x
k
M
nk
|k
|ψ=QFT
+
|
˜
ψ=
N −1
n=0
N −1
k=0
y
n
¯
M
kn
|n,
(19.26)
or, equivalently, for the relations between Fourier and inverse-Fourier components
y
n
, x
k
:
y
n
=n|
˜
ψ=
N −1
k=0
M
nk
x
k
x
k
=k|ψ=
N −1
n=0
¯
M
kn
y
n
.
(19.27)
We have, thus, obtained the most general and very simple definition of the quantum
Fourier operator through its corresponding matrix and its inverse, as applying to a
single qubit of dimension N . We must now find an appropriate quantum circuit, taking
|
ψ
= (x
0
, x
1
,...x
N −1
) as the input, and yielding |
˜
ψ=(y
0
, y
1
,...y
N −1
) as the output,
which would also represent an N -qubit QFT gate. To this purpose, we want to avoid the
complicated implementation of an N × N Vandermonde-matrix gate, and rather seek
for a greatly simplified circuit based on 2 × 2 gates. As this search is a bit tedious and
somewhat tricky in formal derivation, here I shall directly give the conclusion, while the
complete derivation is detailed in Appendix Q. However, the result turns out to be rela-
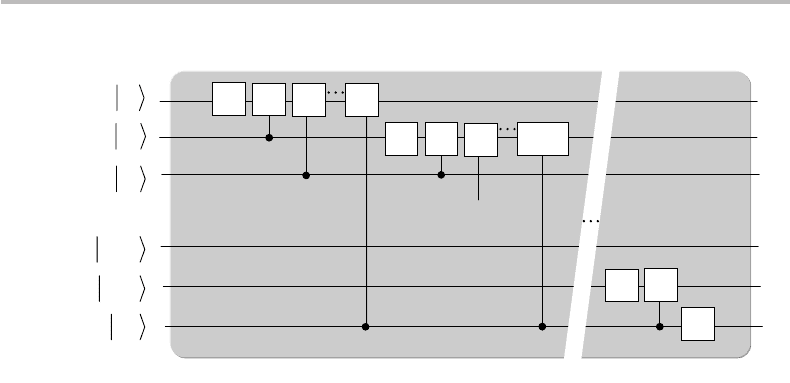
tively simple. The QFT circuit and its constituent 2 ×2 gates are represented in Fig. 19.4.
As a first observation, there are only K = log
2
N qubit inputs, and as many qubit outputs,
labeled in the reverse order. To explain the reduced circuit size, consider, for simplicity,
the case K = 3(N = 8). The relation between the K = 3 inputs {|n
1
, |n
2
, |n
3
} and
