Desurvire E. Classical and Quantum Information Theory: An Introduction for the Telecom Scientist
Подождите немного. Документ загружается.

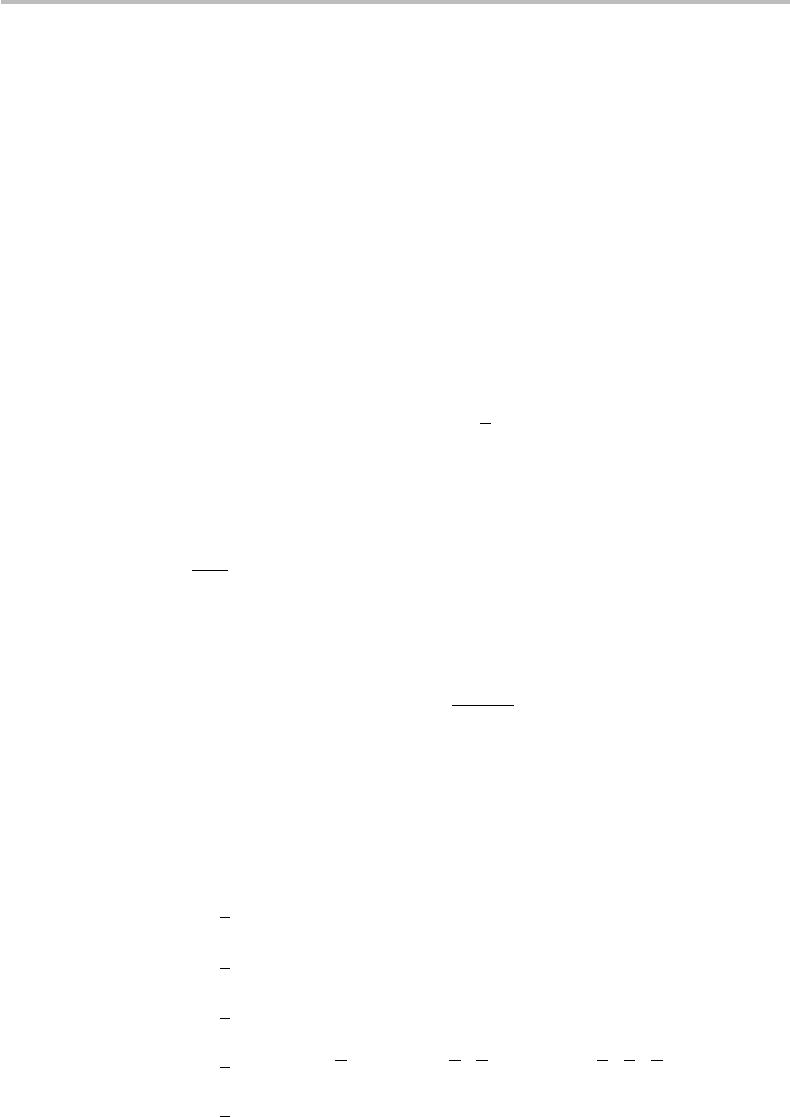
19.3 Quantum Fourier transform algorithm 387
the N = 8 basis states {|0, |1, |2, |3, |4, |5, |6, |7} is given by the binary–tensor
representation of the latter, namely, {|000, |001, |010, |011, |100, |101, |110,
|111}. Thus, the QFT of the basis state |6=|110 is given by the circuit input
{|0, |1, |1}, for instance (starting from the bit of lower weight). As it turns out, the
order of the output qubits is reversed, and the full implementation of the QFT requires
an additional series of SWAP gates. Such a SWAP operation can be performed by a
cascade of three CNOT gates (see Fig. 16.3).
The second observation is that the circuit in Fig. 19.4 is exclusively made of unitary
gates, namely Hadamard (H) and controlled-phase (R
n
) gates. This establishes the fact
that QFT is both a unitary and reversible transformation (using the circuit from left to
right corresponding to the inverse QFT). As shown in Appendix Q, the controlled-phase
gates are defined as follows:
R
n
=
10
0
e
2
i
π
2
n
, (19.28)
noting that this 2 × 2 representation is a reduced one (from Chapter 16, we know that
a controlled-U gate has a 4 × 4 matrix). As detailed in Appendix Q, the output of the
QFT circuit corresponds to the overall tensor product
QFT|n=
1
2
K /2
(|0
1
+
e
2
i
π
1
|1
1
) ⊗ (|0
2
+
e
2
i
π
2
|1
2
) ⊗ ...⊗ (|0
K
+
e
2
i
π
K
|1
K
),
(19.29)
where each output |m=(|0
m
+
e
2
i
π
m
|1
m
) is characterized by the phase factor:
m
=
m
l=1
n
K −m+l
2
l
. (19.30)
I shall now provide two examples, to illustrate how the QFT circuit operates. Consider
first the case K = 2(N = 4), corresponding to a 2-qubit quantum circuit. Figure 19.5
shows the corresponding layout, consistent with that shown in Fig. 19.4. The SWAP gate
to restore the order of qubits is also included for QFT circuit completion. According to
Eq. (19.30), and after the swapping operation, the circuit output is:
QFT
|
n
1
n
2
=
1
2
(|0
2
+
e
2
i
π
2
|1
2
) ⊗ (|0
1
+
e
2
i
π
1
|1
1
)
=
1
2
(|00+
e
2
i
π
1
|01+
e
2
i
π
2
|10+
e
2
i
π(
1
+
2
)
|11)
21
=
1
2
(
|
00
+
e
2
i
π
1
|
10
+
e
2
i
π
2
|
01
+
e
2
i
π(
1
+
2
)
|
11
)
12
=
1
2
#
|
00
+
e
2
i
π
n
2
2
|
10
+
e
2
i
π
(
n
1
2
+
n
2
4
)
|
01
+
e
2
i
π
(
n
2
2
+
n
1
2
+
n
2
4
)
|
11
$
12
≡
1
2
|
00
+ ω
2n
2
|
10
+ ω
2n
1
+n
2
|
01
+ ω
2n
1
+3n
2
|
11
12
,
(19.31)
where I have introduced ω = exp(2
i
π/2
K
) ≡ exp(
i
π/2). In the orthonormal basis
{|
n
1
n
2
}
=
{|
00
,
|
01
,
|
10
,
|
11
}
(taking note here of the binary ordering), we obtain

388 Quantum database search algorithms
1
n
2
n
1
2
1
2
H
H
2
R
Figure 19.5 QFT circuit for K = 2(N = 4).
from Eq. (19.31) the following matrix representation of the QFT circuit:
M =
1
2
11 1 1
1 i −1 −i
1 −11−1
1 −i −1 i
≡
1
√
2
2
1111
1 ωω
2
ω
3
1 ω
2
ω
4
ω
6
1 ω
3
ω
6
ω
9
.
(19.32)
The right-hand side of Eq. (19.32) is recognized as the 4 ×4 Vandermonde matrix, which
was defined in Eq. (19.25) in the general case, i.e., for all K , with ω = exp(2
i
π/2
K
).
This result is, therefore, consistent with all QFT definitions previously derived in this
section. An interesting application example is the quantum Fourier transform of the
EPR–Bell states,
+
+
β
ij
=
, which is left as a straightforward exercise to calculate, using the
above matrix (there is no big point about the result, except for the conclusion that QFT
maintains a state of entanglement, under a more complex state mixture).
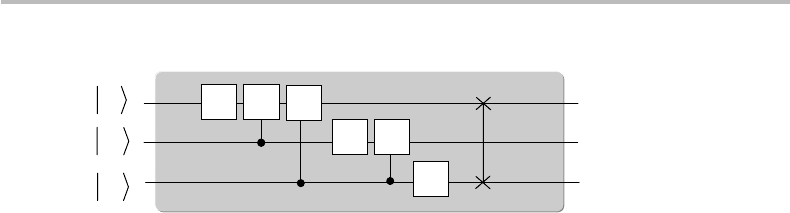
The QFT circuit shown in Fig. 19.6 corresponds to the case K = 3(N = 8), including
the SWAP ordering operation. There is no point in expanding Eq. (19.29) again to define
the 3-qubit circuit output explicitly. We simply need to substitute ω = exp(2
i
π/2
3
) ≡
exp(
i
π/4) into the 8 ×8 Vandermonde matrix in Eq. (19.25), which, taking into account
the ω periodicity yields:
M =
1
√
2
3
11111111
1 ωω
2
ω
3
ω
4
ω
5
ω
6
ω
7
1 ω
2
ω
4
ω
6
ω
8
ω
10
ω
12
ω
14
1 ω
3
ω
6
ω
9
ω
12
ω
15
ω
18
ω
21
1 ω
4
ω
8
ω
12
ω
16
ω
20
ω
24
ω
28
1 ω
5
ω
10
ω
15
ω
20
ω
25
ω
30
ω
35
1 ω
6
ω
12
ω
18
ω
24
ω
30
ω
36
ω
42
1 ω
7
ω
14
ω
21
ω
28
ω
35
ω
42
ω
49
≡
1
2
√
2
11111111
1 ωω
2
ω
3
ω
4
ω
5
ω
6
ω
7
1 ω
2
ω
4
ω
6
1 ω
2
ω
4
ω
6
1 ω
3
ω
6
ωω
4
ω
7
ω
2
ω
5
1 ω
4
1 ω
4
1 ω
4
1 ω
4
1 ω
5
ω
2
ω
7
ω
4
ωω
6
ω
3
1 ω
6
ω
4
ω
2
1 ω
6
ω
4
ω
2
1 ω
7
ω
6
ω
5
ω
4
ω
3
ω
2
ω
.
(19.33)
19.4 Grover quantum database search algorithm 389
1
n
2
n
3
n
1
2
3
1
2
3
H
H
2
R
H
2
R
3
R
Figure 19.6 QFT circuit for K = 3(N = 8).
Is the QFT algorithm any faster than its classical counterpart, which is known as fast
Fourier transform (FFT)? To answer this question, let us analyze the number of gates
traversed by the signals for each circuit type. Referring back to Fig. 19.4, we observe that a
K circuit requires crossing a number of gates of K + (K − 1) + (K − 2) +...2 +1 =
K
k=1
k = K (K + 1)/2, plus K /2or(K − 1)/2(K even or odd) twin gates to perform
the SWAP operation, each amounting to three CNOT gates. We can conclude that the
computation time for a QFT circuit of K inputs to generate the output is of the order
of K
2
, noted O(K
2
). In computer language, it is said that this algorithm (or decision
problem) belongs to the complexity class P, as the implementation in a sequential
machine can be performed in polynomial time.
4
In contrast, the number of gates required in a classical FFT circuit for the same
computation (data size N = log
2
K )isK log K = 2
N
log
2
2
N
= N 2
N
. Thus, the FFT
computation time is of the order O(N 2
N
), which is exponential in circuit size, as opposed
to quadratic in the QFT case. Such a comparison remains, however, questionable, because
the quantum circuit does not operate on data bits, but quantum states. Further processing
circuits would be required to measure the “classical bit” or cbit counterparts, but even
this observation fails to convey any equitable comparison, as such measurements are,
by nature, indeterministic. Simply put, the QFT is exponentially faster than FFT, but the
signal amplitudes cannot be measured, unlike in the classical case. The picture becomes
even darker if we consider that there is currently no known technique to prepare the
input states
|
n
k
of the QFT circuit, except in the very limiting cases K = 1orK = 2.
The quantum Fourier transform may, thus, appear to be fully impractical, or just an
interesting mathematical curiosity. As we shall see in Chapter 20, however, the QFT
algorithm is the key to solving one of the major computation problems, namely the
factoring of numbers into primes, famously known as the Shor algorithm.
19.4 Grover quantum database search algorithm
In this section, I describe another famous QC algorithm, known after its conceiver as
the Grover quantum database search (GQDS). Like the previously described QFT, this
algorithm nicely exploits the property of quantum parallelism.
4
This notion is not to be confused with the time required for solution verification, which is referred
to as an NP (indeterministic polynomial time) problem. See more on this topic, for instance in:
http://en.wikipedia.org/wiki/Complexity_classes_P_and_NP.

390 Quantum database search algorithms
The problem to solve here is quite basic: how to identify an item out of an unsorted
database of N distinct elements? On average, such a task would require N/2 searches,
with a worst case of N searches and a luckiest case of one single search. The computation
time to find any item is, therefore, of the order of N ,or
O
(N ). As we shall see, the beauty
in the GQDS algorithm is that the complexity of the search task becomes
O
(
√
N ), which
means a quadratic increase in computing speed.
Here, I shall first describe the GQDS algorithm and then analyze its elementary
quantum-circuit implementation and requirements.
5
There is no loss in generality in assuming that the size of the database is N = 2
n
,
where n is some nonzero integer. We require a quantum space V of dimension N ≥ 2,
and a known observable on this space. This observable defines an orthonormal
basis of N eigenstates |x labeled |0, |1,...,
|
N − 1
, and known eigenvalues labeled
λ
0
,λ
1
,...,λ
N −1
. Then we shall associate a unique eigenstate or eigenvalue with each
item in the database. The database search problem is now a matter of measuring an
eigenvalue of interest, call it λ
ω
, associated with the state
|
ω
, which represents some
specific item ω in the original database, and which we want to find through the search
algorithm.
As I will show further on, it is possible to construct the eigenstate superposition
|
s
=
1
√
N
N −1
x=0
|x, (19.34)
noting that s|s=1 since the eigenstate basis {|x}
x=0...N −1
is orthonormal. Any eigen-
state |ω has the same projection ω|s=1/
√
N , and given our item ω, the probability
of measuring λ
ω
(or finding |s in the state |ω)is|ω|s|
2
= 1/N , consistently with a
classical database search algorithm. Let us then introduce a unitary operator U
ω
, referred
to as the “oracle,” and defined by
U
ω
= I − 2|ωω|. (19.35)
It is immediately verified that the oracle has the following properties: U
ω
|x=−
|
ω
if
x = ω and U
ω
|x=|x if x = ω. Thus, the action of the oracle on the superposition
|
s
is to change the sign of the amplitude of the component
|
ω
in
|
s
, namely:
|
ψ
= U
ω
|
s
= U
ω
3
1
√
N
N −1
x=0
|x
4
=
1
√
N
U
ω
N −1
x=0
x=ω
|x+
|
ω
5
See, for instance, http://en.wikipedia.org/wiki/Grover’s_algorithm with notations consistent with those used
in this section. The description here is inspired from the tutorial paper: C. Lavor, L. R. U. Manssur,
and R. Portugal, Grover’s algorithm: quantum database search, (2003), which can be downloaded from
http://arxiv.org/abs/quant-ph/0301079.
19.4 Grover quantum database search algorithm 391
=
1
√
N
N −1
x=0
x=ω
U
ω
|x+U
ω
|ω
≡
1
√
N
N −1
x=0
x=ω
|x−
1
√
N
|ω. (19.36)
We can also rewrite the result in Eq. (19.36) in the form:
|
ψ
= U
ω
|s=
|
s
−
2
√
N
|
ω
. (19.37)
We can then interpret the action of the oracle U
ω
of the state
|
s
as a small rotation
through an angle θ. Indeed, we have
cos θ =s|ψ
=s|s−
2
√
N
s|ω
= 1 −
2
√
N
1
√
N
≡ 1 −
2
N
(19.38)
(the angle θ being small, if one assumes that the database size, N, is large). Next we
introduce a second operator U
s
according to
U
s
= 2
|
s
s
|
− I, (19.39)
and define the Grover operator as G = U
s
U
ω
. Let us see next the action of this operator
on
|
s
, which we shall refer to as a Grover iteration.FromEq.(19.37),wehave:
|ψ
1
=G|s=U
s
U
ω
|s=U
s
|ψ=U
s
|s−
2
√
N
|ω
= U
s
|s−
2
√
N
U
s
|ω
=
(
2|ss|−I
)
|s−
2
√
N
(
2|ss|−I
)
|ω
= 2|ss|s−|s−
4
√
N
|ss|ω+
2
√
N
|ω
=|s−
4
√
N
1
√
N
|s+
2
√
N
|ω
≡
1 −
4
N
|s+
2
√
N
|ω.
(19.40)
We observe from the result in Eq. (19.40) that the action of G on |s is to increase
the amplitude of the eigenstate component |ω, again by rotation. The corresponding
392 Quantum database search algorithms
rotation angle θ
is given by
cos θ
=s|ψ
1
=s|
1 −
4
N
|s+
2
√
N
|ω
=
1 −
4
N
s|s+
2
√
N
s|ω
= 1 −
4
N
+
2
√
N
1
√
N
≡ 1 −
2
N
≡ cos θ,
(19.41)
and according to Eq. (19.38), which shows that the rotation angles θ,θ
due to U
ω
and
G are equal in absolute value. It is easy to show that |ψ=U
ω
|s and |ψ
1
=G|s are,
in fact, rotating by that same absolute angle θ = θ
in opposite directions away from |s,
forming an angle θ
= 2θ. Indeed, from Eqs. (19.37) and (19.40) we obtain:
cos θ
=
ψ|ψ
1
=
s|−
2
√
N
ω
|
1 −
4
N
|s+
2
√
N
|ω
=
1 −
4
N
s|s
−
2
√
N
1 −
4
N
ω|s
+
2
√
N
s|ω
−
2
√
N
2
√
N
ω|ω
= 1 −
4
N
−
2
√
N
1 −
4
N
1
√
N
+
2
√
N
1
√
N
−
4
N
≡ 1 −
8
N
+
8
N
2
≡ 2
1 −
2
N
2
− 1 ≡ 2 cos
2
θ −1 ≡ cos 2θ. (19.42)
Finally, it is straightforward from the definitions in Eq. (19.40) that the cosine projection
of |ψ
1
over the target state |ω takes the value
ω|ψ
1
= (3 − 4/N )/
√
N , to compare
with the initial projection
ω|s
= 1/
√
N . The angle relations of the different states
|s, |ψ, |ψ
1
, and |ω and relevant projections
ω|s
,
ω|ψ
1
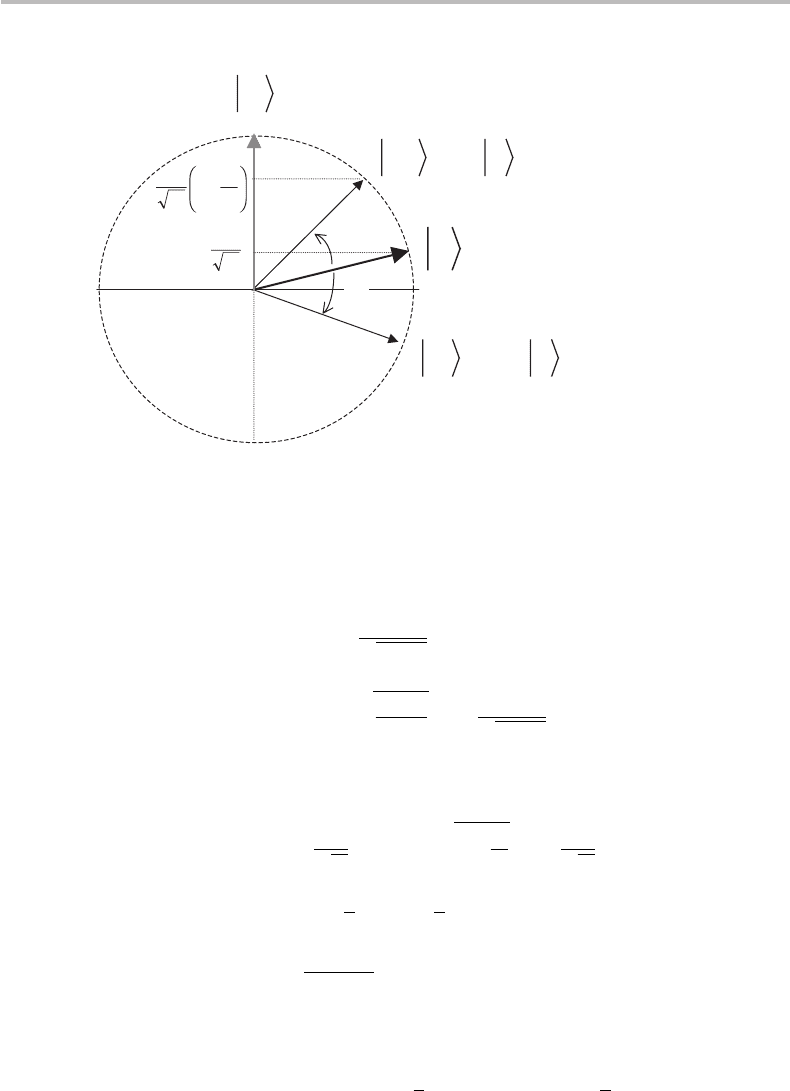
are illustrated in Fig. 19.7.
We observe from the figure that G has rotated |s into a state |ψ
1
, which is closer to
the target state |ω, hence a projection being increased by a factor 3 −4/N (which is
greater than unity if N > 2). Should a measurement in the state |ψ
1
be made through
the observable , the probability of measuring λ
ω
would be
|
ω|ψ
1
|
2
=
1
N
3 −
4
N
2
=
1
N
9 −
24
N
+
16
N
2
≈
9
N
, (19.43)
the upper limit on the right-hand side being obtained for large values of N . This result
shows that in a single Grover iteration, the probability of finding the searched item
through a single-shot measurement has been increased by about tenfold with respect to
the classical case.
It is now tempting to iterate the Grover operation as many times as required to rotate the
system state closer to the target state |ω, thus, increasing the probability of successfully
measuring λ
ω
to the required accuracy. For this, we must establish an iterative formula
that defines the state
|
ψ
k
after k Grover iterations, and the corresponding success
probability.
For the purpose of deriving the iteration formula, let us redefine the original eigenstate
superposition in Eq. (19.34) by sorting out the |ω state from the series. Define first the
19.4 Grover quantum database search algorithm 393
'
θ
θ
ω
s
sU
ω
ψ
=
sG=
1
ψ
N
1
−
N
N
4
3
1
Figure 19.7 Effect of the unitary operators U
ω
and G = U
s
U
ω
on initial state |s, showing
rotation by angles θ and θ
= θ (respectively) corresponding to new states |ψ=U
ω
|s and
|ψ=G|s (respectively). The cosine-projections of states |s and |ψ
1
over the reference state
|ω of the search algorithm are also indicated.
state |u spanning the hyperspace orthogonal to |ω according to
|u≡
1
√
N − 1
N −1
x=0
x=ω
|x
=
5
N
N − 1
|s−
1
√
N − 1
|ω.
(19.44)
We can then write |s according to the superposition of its two orthogonal component
states |u, |ω:
|s=
1
√
N
N −1
x=0
|x≡
5
1 −
1
N
|u+
1
√
N
|ω
≡ cos
θ
2
|u+sin
θ
2
|ω,
(19.45)
where θ is the rotation angle previously defined through cos θ = 1 −2/N (it is easily
checked that cos θ/2 =
√
1 − 1/N ). It is then an elementary (albeit nontrivial) exercise
to show that k Grover iterations result in the state
G
k
|s=
(
GG ...G
)
k times
|s
= cos
(
2k + 1
)
θ
2
|u+sin
(
2k + 1
)
θ
2
|ω.
(19.46)
This result shows that k applications of the Grover operator results in the rotation of the
state |s by an angle kθ , as illustrated in Fig. 19.8. The probability p(ω) of finding the
state G
k
|s in |ω, and, hence, of measuring the eigenvalue λ
ω
with the observable ,is
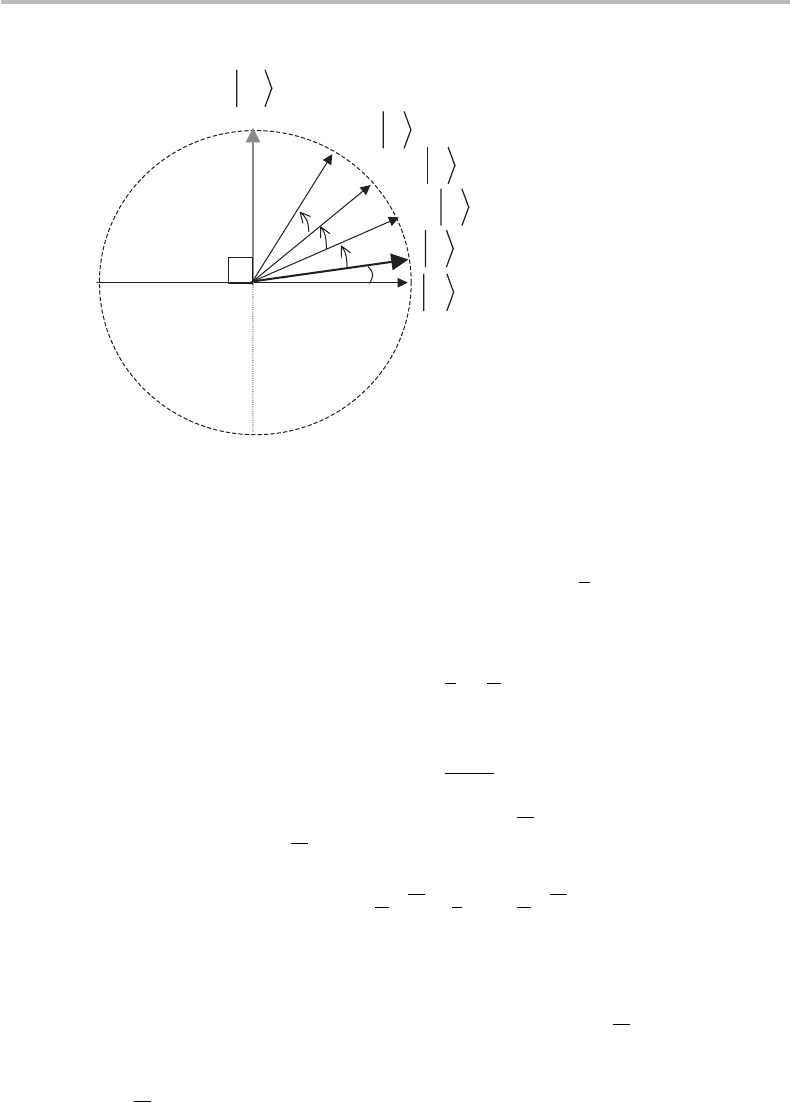
394 Quantum database search algorithms
θ
2/
θ
ω
u
sG
s
θ
sG
2
θ
sG
3
Figure 19.8 Effect of successive applications (here from k = 1tok = 3) of the Grover operator
G onto the initial state |s, showing incremental rotations by angle θ in the direction of state |ω.
given by
p(ω) =
+
+
ω
|
G
k
|s
+
+
2
= sin
2
(
2k + 1
)
θ
2
. (19.47)
The probability p(ω) reaches a maximum for
k
max
θ +
θ
2
=
π
2
, (19.48)
or
k
max
=
>
π −θ
2θ
?
. (19.49)
From the definition in Eq. (19.45),sinθ/2 = 1/
√
N , which for large N yields the
approximation θ ≈ 2/
√
N and, hence, the maximum number of iterations k
max
:
k
max
≈
>
π
4
√
N −
1
2
?
≈
@
π
4
√
N
A
. (19.50)
Clearly, the Grover search algorithm must be stopped after reaching the number of
iterations k = k
max
, corresponding to the probability p(ω) ≈ 1. Figure 19.9 shows plots
of the probability p(ω), a function of the number k of Grover iterations, from quantum
database sizes N = 2
6
= 64 to N =2
14
=16 384. Thanks to the
√
N dependence of k
max
,
it is seen that quantum databases as large as N ≈ 16 000 can successfully be searched
with only k
max
≈ 100 Grover iterations, which represents a computation complexity in
O
(
√
N ), to compare with
O
(N ) in the classical case.
Now that we are convinced of the benefits of the Grover algorithm, the next step is to
analyze its quantum-circuit implementation. Consider first how the quantum database
can be generated. In Section 19.2, concerning the Deutsch–Jozsa algorithm, we have
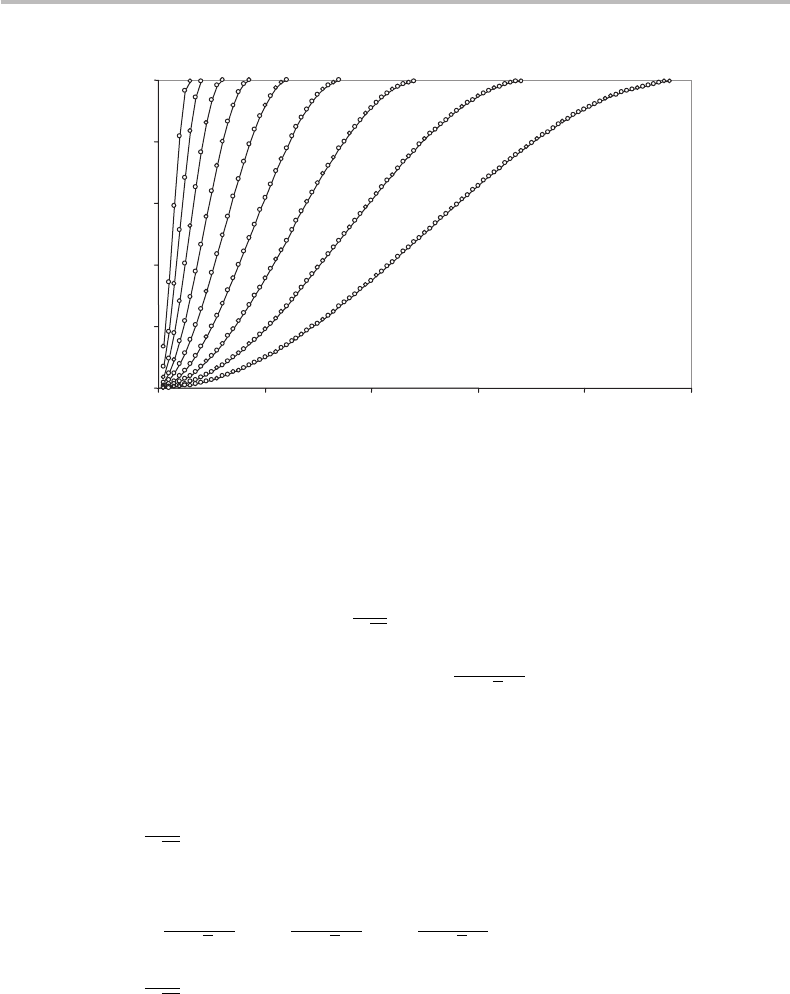
19.4 Grover quantum database search algorithm 395
0.0
0.2
0.4
0.6
0.8
1.0
0 20406080100
number of measurements k
Probability p(
w
)
64
128
256
512
1.024
2.048
4.096
8.192
16.384
=
N
Figure 19.9 Probability p(ω) of finding the state in |ω (or of measuring the eigenvalue λ
ω
)asa
function of the number k of Grover iterations, from quantum database sizes N = 2
6
= 64
(leftmost curve) to N = 2
14
= 16 384 (rightmost curve).
established and used in Eq. (19.7) the property according to which
|s=
1
√
N
N −1
x=0
|x
= H
⊗n
|0=
|0+|1
√
2
⊗n
=
|
+
⊗
|
+
⊗ ...⊗
|
+
n times
,
(19.51)
where H
⊗n
is the n-tensor application of the Hadamard gate H . For instance, we have,
for N = 2
3
= 8:
|s=
1
√
2
3
7
x=0
|x
= H
⊗3
|0
=
|0+|1
√
2
⊗
|0+|1
√
2
⊗
|0+|1
√
2
≡
1
√
2
3
(|000+|001+|010+|011+|100+|101+|110+|111).
(19.52)
Thus, the state superposition |s, which is to become the quantum database, can be
generated by using n ancilla qubits |0 and 2 × 2 Hadamard gates H .
The second task is to define a quantum circuit for the “oracle” operator U
ω
. To recall,
the oracle has the following properties: U
ω
|x=−|ω if x = ω and U
ω
|x=|x if
x = ω.Let f (x) be a function defined over x =
{
0, 1,...,N − 1
}
with binary output
f (x) = 1ifx = ω and f (x) = 0ifx = ω. Assume that it is possible to build a quantum
circuit (or quantum operator U
ω
) acting on the tensor state |x
|
i
(with
|
i
=|0 or |1

396 Quantum database search algorithms
being an ancilla qubit) yielding the following output:
U
ω
|x|i=|x|i ⊕ f (ω). (19.53)
It is clear from the above definitions that U
ω
|x
|
i
=|x
|
i
if x = ω and U
ω
|x
|
i
=
|x|i ⊕ 1 if x = ω. More generally, if we let
|
i
=
|
−
=
(
|0−|1
)
/
√
2, we obtain
U
ω
|x|− = U
ω
|x
|0−|1
√
2
=|x
|
0 ⊕ f (ω)
−
|
1 ⊕ f (ω)
√
2
=|x
|
f (ω)
−
|
1 ⊕ f (ω)
√
2
=
|x
|0−|1
√
2
, if x = ω
|x
|1−|0
√
2
, if x = ω
≡
(
−1
)
f (ω)
|x|−.
(19.54)
Call the tensor state |R=|s|− the “register” in the GQSD algorithm. If we apply
the oracle U
ω
to the register
|
R
, and use the definitions in Eqs. (19.34) and (19.54),we
obtain:
U
ω
|
R
= U
ω
|s|−
= U
ω
3
1
√
N
N −1
x=0
|x|−
4
=
1
√
N
U
ω
3
N −1
x=0
|x|−
4
=
1
√
N
N −1
x=0
x=ω
U
ω
|x|− +U
ω
|ω|−
=
1
√
N
N −1
x=0
x=ω
(−1)
0
|x|− + (−1)
1
|ω|−
≡
1
√
N
N −1
x=0
x=ω
|x|− − |ω
|−,
(19.55)
which is precisely the oracle operation defined in Eq. (19.36). Since we have assumed
that the oracle operator U
s
= I − 2|ωω| can be thus realized, we can also assume that
similarly, one can realize the unitary transformation U
s
= 2|ss|−I , in similar ways
(this being beyond the scope of this book).
