Desurvire E. Classical and Quantum Information Theory: An Introduction for the Telecom Scientist
Подождите немного. Документ загружается.

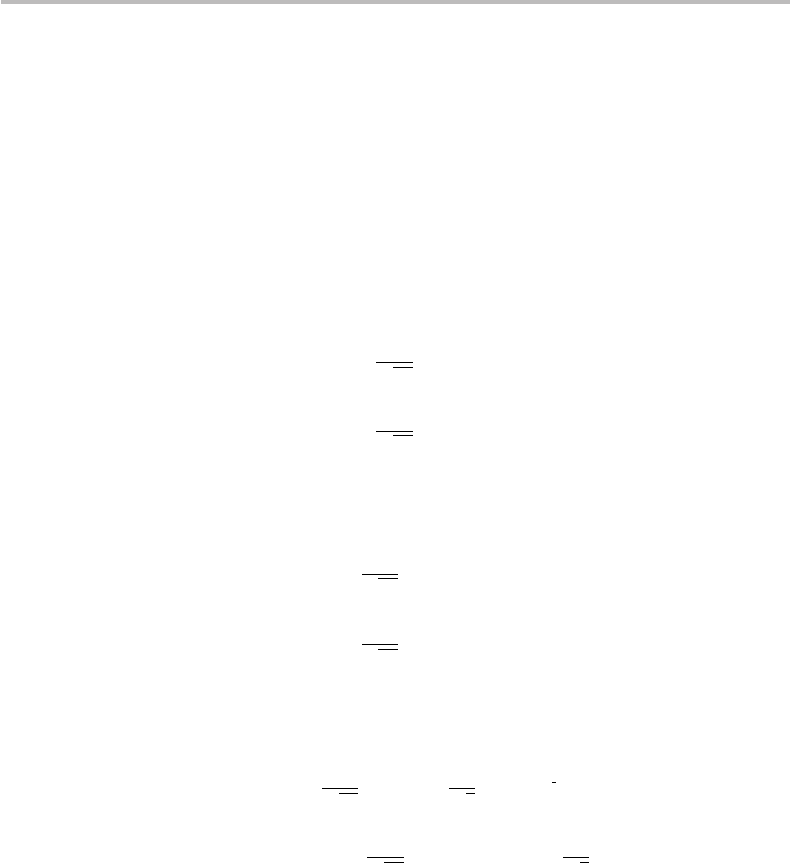
20.2 Order finding 407
of operator U , as defined in Eq. (20.12), to the power j = 2
0
, 2
1
...2
K −1
= 1 ...K .
Consistently, we have for the target qubit |1
CU
j
(|0⊗|1) =|1
CU
j
(|1⊗|1) =|x
j
mod N .
(20.17)
As seen from Fig. 20.3, the combined register input (➀)is
|
ψ
1
=|0
⊗K
⊗|1. (20.18)
After passing through the Hadamard gate (➁) the state has evolved into
3
|
ψ
2
=
1
√
M
(
|0+|1
)
⊗K
⊗|1
=
1
√
M
M−1
j=0
|
j
⊗|1,
(20.19)
with M = 2
K
, as a recall. After application of the controlled-U
j
gate (➂) we obtain the
state
|
ψ
3
=
1
√
M
M−1
j=0
CU
j
|
j
⊗|1
=
1
√
M
M−1
j=0
|j⊗|x
j
mod N .
(20.20)
Substituting then the property in Eq. (20.16), effecting the index change j → k for
reading convenience, and introducing ϕ
s
= s/r , we obtain, equivalently:
|
ψ
3
=
1
√
M
M−1
k=0
|k⊗
1
√
r
r−1
s=0
e
2
i
πk
s
r
|
u
s
=
r−1
s=0
3
1
√
M
M−1
k=0
e
2
i
πkϕ
s
|
j
4
⊗
1
√
r
|u
s
.
(20.21)
Next, in ➃ we apply the inverse Fourier transform to the first register, whose contents are
expressed in parenthesis in Eq. (20.21). In this expression, we recognize the same state
superposition as in Eq. (20.9). As we have previously seen, the inverse Fourier transform
of this superposition leads to a fair approximation
|
˜ϕ
s
of the state
|
ϕ
s
. Therefore, the
3
For the tensor product to the summation conversion, see previous note, while setting ϕ = 0. In Eq. (20.20),
we also used the property according to which
CU
j
|j ⊗|1=
+
+
+
x
j
1
2
K −1
mod N
/
+
+
+
x
j
2
2
K −2
mod N
/
···
+
+
+
x
j
K
2
0
mod N
/
=
+
+
+
x
j
1
2
K −1
× x
j
2
2
K −2
×···×x
j
K
2
0
mod N
/
=
+
+
+
x
j
1
2
K −1
+j
2
2
K −2
+···+j
K
2
0
mod N
/
≡|x
j
mod N .

408 Shor’s factorization algorithm
circuit output can be expressed in the form:
|
ψ
4
=
1
√
r
r−1
s=0
|
˜ϕ
s
⊗
|
u
s
. (20.22)
A measurement of the first register projects the superposition in Eq. (20.22) into one
of the r states
|
ϕ
s
, with uniform probability p(s) = 1/r, which then yields the ratio
s/r , corresponding to the phase estimation ˜ϕ
s
≈ ϕ
s
= s/r associated with the eigenstate
|
u
s
.
As discussed in the previous section, if the control register size, K ,issettoK =
l +log
2
[2 + 1/(2ε)], the measurement ˜ϕ
s
is an approximation of ϕ
s
= s/r that is
accurate up to 2
−l
, with a probability of success of at least 1 −ε. Assume here that we
require an accuracy of l = 2L + 1 bits, a specific but most useful condition that will be
justified later. The control register size is, thus, set to K = 2L + 1 +log
2
[2 + 1/(2ε)].
The next step consists in the evaluation of the number r , given the knowledge of the
˜ϕ
s
measurement, with s ∈
{
0, 1, 2,...,r − 1
}
being random, and the fact that s/r < 1
is a rational number, i.e., the ratio of two bounded integers, p, q. The determination of
r requires a classical computation, which is based on the continued fraction expansion
algorithm described in the next section.
20.3 Continued fraction expansion
In this section, I introduce the continued fraction expansion (or continued fraction
algorithm), and show how it can be applied to determine an integer r from a given
rational number s/r < 1.
The principle of the expansion is to express a rational number a = p/q, with p, q
having no common factor, into a unique and finite suite, or expansion of positive integers
[
a
0
, a
1
,...,a
n
]
and satisfying
a = a
0
+
1
a
1
+
1
a
2
+
1
···+
1
a
n
. (20.23)
To provide an example, take a = 57/21. We obtain
57
21
= 2 +
15
21
= 2 +
1
21
15
= 2 +
1
1 +
6
15
= 2 +
1
1 +
1
15
6
= 2 +
1
1 +
1
2 +
3
6
≡ 2 +
1
1 +
1
2 +
1
2
,
(20.24)

20.3 Continued fraction expansion 409
which yields the expansion
[
2, 1, 2, 2
]
. We note that the iteration of this “split and
invert” expansion always stops at some point, since the numerator in the last fraction at
the bottom at each step decreases, eventually reducing to one. The lesson learnt is that
any rational number a = p/q lends itself to a continued fraction expansion having a
unique signature suite
[
a
0
, a
1
,...,a
n
]
.
Given the measurement ˜ϕ = x, with x being some approximation of ϕ = s/r , our
task is now to identify a rational number s/r, called convergent of x, which may closely
approach x. To do this, we must use some key properties of the continued fraction
expansion, which are described in Appendix R. Here, we shall only need the final
property. This property states that given a rational number x, and two co-prime integer
numbers s, r satisfying
+
+
+
s
r
− x
+
+
+
≤
1
2r
2
, (20.25)
the ratio s/r is convergent on x. This is where the choice of register size and phase
accuracy we made in the previous section comes into the picture and becomes justified.
With such a choice, indeed, we know that the phase estimation x is accurate up to
2
−l
= 1/2
2L+1
. Since we inherently have r ≤ N , and also N ≤ 2
L
by definition, we
have r ≤ N ≤ 2
L
, thus, 1/(2r
2
) ≤ 1/2
2L+1
and, therefore, the condition in Eq. (20.25)
applies. The continued fraction expansion of ˜ϕ = x, can be computed classically through
the algorithm described in Appendix R, as also illustrated with a practical numerical
example. The algorithm yields a finite series of rational numbers s
/r
, which from the
above condition, are known to be convergent on s/r . The convergent s
/r
that most
closely approaches the upper bound defined in Eq. (20.25) is the one for which r
= r,
concluding the search.
The following discussion, which can be skipped to keep the focus on this chapter,
addresses some fine points about the success probability and the implementation cost
of the order-finding algorithm. Suffice it to state that the algorithm efficiently yields the
order of N and that the complexity or cost is
O
(L
3
), namely, that the answer can be
obtained in polynomial time.
Discussion
(i) Since the above determination of s/r (and hence of r) is only probabilistic, there
exists a finite chance that it may fail. As we have seen, the probability of failure is,
at most, ε, which can be made arbitrarily small through an adequate choice of the
control register size, K . Independently of such probability considerations, checking
whether or not the determination is successful is immediate: it is only necessary
to calculate x
r
mod M and verify that the result is unity. In case of failure, the
algorithm may be repeated, with the probability of failing again being, at most, ε
2
.
Another possibility of failure (x
r
mod M = 1) is that s and r turn out to have a
common factor, or be not co-prime. In this case the continued fraction algorithm
yields a multiple of r. Recall that the phase estimation produces an estimate of s/r
with s ∈{0, 1, 2,...,r − 1} being a uniformly distributed random number. There

410 Shor’s factorization algorithm
is, indeed, a finite chance that s, r is not co-prime. It has been established from theory
that the number of primes under a given integer r is at least r/ ln r .
4
This means that
any positive number less than r , as selected at random, has a probability of at least
1/ ln r of being prime. Therefore, the probability that s, r (0 < s < r, r < N )are
co-prime is at least 1/ ln r > 1/ ln N. Hence, it takes one to implement the phase
measurement up to ln N times to obtain with reasonably high probability a co-prime
pair s
, r
for which r
= r.
(ii) What is the cost of implementing the order-finding algorithm? Looking at
Fig. 20.3, we observe that the corresponding quantum circuit includes (a) K
Hadamard gates (H
⊗K
), (b) an L-qubit modular-exponentiation circuit (U
j
),
and (c) a K -qubit inverse Fourier transform circuit (FT
+
). Since K = 2L + 1 +
log
2
[2 + 1/(2ε)],givenε the number of required gates in case (a) is of the order
O(L), and in case (c) it is of the order O(K
2
) = O(L
2
), as established in Chapter
19. The modular exponentiation in case (c) requires a number of gates of the
order of O(L
3
). This is explained by the fact that computing |x
j
mod N , with
j = 0, 1 ...2
K
, requires up to K − 1 modulo N squaring operations (x
2
1
= (x
2
0
)
2
,
x
2
2
= (x
2
1
)
2
,..., x
2
K −1
= (x
2
K −2
)
2
, with each squaring operation having a cost of
O(K
2
) gates,
5
resulting in an overall cost of O(K
3
) ≡ O(L
3
) gates. Finally, the con-
tinued fraction expansion, which is to be implemented with a classical computer,
has a cost of O(L
3
) elementary operations. This is because the algorithm takes L
split-and-invert steps, since s, r are L-bit integers, each of these steps requiring a
number of basic arithmetic operations of the order O(L
2
) (see Appendix R, namely,
the operations u
n
= 1/(u
n−1
− a
n−1
) and the validation test 1/2q
2
n
− in Table
R1). The key conclusion is that the order-finding algorithm has a complexity of
O(L
3
) and, therefore, can be run in polynomial time.
20.4 From order finding to factorization
In this section, we describe how the quantum order-finding algorithm makes it possible to
factorize composite numbers into primes, a problem also known as prime decomposition.
Before going into the mathematical detail of the description, it is useful to outline the
problem of factorizing composite numbers and its difficulty, as viewed from a classical
computation perspective.
It is a fundamental property that all integer numbers can be uniquely generated by
products of prime numbers and their powers. This is illustrated in Table 20.2 for numbers
up to N = 30.
6
By definition, a composite number is a product of at least two prime
numbers. For numbers up to a few hundreds, the task of factorizing can be performed
4
The number of primes less than x corresponds to the heuristic function called π(x). The “prime number
theorem” states that the number of primes not exceeding x is asymptotic to x/ ln x. Actually, a finer approx-
imation to π(x)isx/(ln x − 1). For reference, see, for instance, http://primes.utm.edu/howmany.shtml.
5
Indeed, it is easily checked that multiplying two numbers with N and M decimals (or bits) requires N × M
individual multiplications and N × M − 1 additions of the resulting terms. The number of gates is thus
O(N × M), or O(N
2
) for a squaring operation (N = M).
6
A complete list of prime factors up to N = 1000 is available at http://en.wikipedia.org/wiki/Table_
of_prime_factors.

20.4 From order finding to factorization 411
Table 20.2 Factorization of integers into primes up to N = 30.
NN N N N N
1– 62×311 1116 2
4
21 3 ×726 2×13
22 7 7122
2
× 317 7222× 11 27 3
3
33 8 2
3
13 13 18 2 × 3
2
23 23 28 2
2
× 7
42
2
93
2
14 2 ×719 19242
3
× 329 29
55102×515 3× 5202
2
× 525 5
2
30 2 ×3 ×5
mentally. This is because we have our multiplication tables memorized, which leaves
out a list of the first prime numbers: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43,
47, . . . It only takes a few divisions to hit one or two numbers from such a short list. For
greater numbers that can be entered into a pocket calculator or a computer spreadsheet,
the problem of factorizing is also elementary. The basic approach consists of the routine
of successively attempting to divide N by all known prime numbers lower than
√
N , and
repeating such a trial division until complete prime factoring is obtained. Extensive lists
of the known prime numbers, up to 15 million, are available on the Internet,
7
making
it possible to implement such a trial division algorithm. More practical and efficient
algorithms exist, however, named after Pollard, William, Lenstra, Fermat, Dixon, and
Shank, and also under different variants of the so-called “number field sieve.”
8
The
most efficient one is the general number field sieve (GNFS) algorithm, which applies
to numbers having more than 100 binary digits. It is not the point here to describe the
GNFS algorithm and its variants, but only to mention that its complexity (the minimum
computing program length, see Chapter 7) is defined by:
9
C = exp
[
const + O(1)
]
×
(
ln N
)
1
3
(
ln ln N
)
2
3
. (20.26)
It can be shown that the best GNFS algorithm variant has a computational order of
O
exp
64
9
(
ln N
)
1
3
×
(
ln ln N
)
2
3
%
= O
exp
64
9
k
1
3
×
(
ln k
)
2
3
%
, (20.27)
where k ≈ log N is the binary size of the number N to be factorized. Thus, classical
implementation of prime decomposition is subexponential,butsuperpolynomial in num-
ber (bit) size. To show that the above conclusion is not innocuous, assume that the size is
k = 100. We obtain from Eq. (20.27) the result O
[
f (N )
]
≈ 4.7 × 10
39
.Fork = 1000,
we obtain O
[
f (N )
]
≈ 1.0 × 10
112
. For a classical computer having the computing power
of one Giga (10
9
) operations per second,or3× 10
16
operations per year, just factoring a
k = 100 number according to GNFS would require some 23 years, or, say, implementing
about 100 such computers running in parallel for a duration of three months. We should
now be convinced, if needed, that the factoring problem is nontrivial when it comes to
relatively large numbers. This point is illustrated by the RSA challenge.
10
The company
7
See, for instance: http://en.wikipedia.org/wiki/List_of_prime_numbers; www.math.utah.edu/∼pa/math/
primelist.html; http://primes.utm.edu/lists/small/1000.txt; http://primes.utm.edu/lists/small/millions/.
8
See http://en.wikipedia.org/wiki/Integer_factorization.
9
See http://en.wikipedia.org/wiki/General_number_field_sieve.
10
See www.rsa.com/press_release.aspx?id=3520.

412 Shor’s factorization algorithm
RSA offers substantial prizes for teams who may succeed in factoring composite num-
bers of various sizes, i.e., given N, finding primes p, q such that N = pq. The latest
challenge to be solved, called RSA_640, was reported on November 2005.
11
The number
to be factorized had 193 digits, corresponding to 640 bits:
N = 3 107 418 240 490 043 721 350 750 035 888 567 930 037 346 022 842 727 545
720 161 948 823 206 440 518 081 504 556 346 829 671 723 286 782 437 916 272
838 033 415 471 073 108 501 919 548 529 007 337 724 822 783 525 742 386 454
014 691 736 602 477 652 346 609,
which decomposes into the two primes:
p = 1 634 733 645 809 253 848 443 133 883 865 090 859 841 783 670 033 092 312 181
110 852 389 333 100 104 508 151 212 118 167 511 579,
q = 1 900 871 281 664 822 113 126 851 573 935 413 975 471 896 789 968 515 493 666
638 539 088 027 103 802 104 498 957 191 261 465 571.
The computation of p, q took the equivalent of 30 CPU years, using 80 processors
at 2.2 GHz clock cycle, and spread over 5 months of calendar time. The highest and
yet unsolved challenge, RSA-2048, is a 2048-bit or 617-digit number. According to
Eq. (20.27), its factorization is of the order O
[
f (N )
]
≈ 8.5 × 10
151
. It is clear that
solving this last challenge will require even more substantial computing power and
resources, along with new and significant progress in factorization algorithms, which
may take a few decades. It is tempting to speculate that, by that time, factorization of
such big numbers might be routinely performed by quantum computers through Shor’s
algorithm! Only history will tell.
We now return to the core subject of this section, which is the connection between
order finding and factoring. This connection requires two key theorems, which I am
going successively to describe, comment, and illustrate with examples. It is assumed
that N is a composite number of size L bits, and that x is an integer number such that
1 ≤ x ≤ N − 1. The notation GCD(n, m) corresponds to the greatest common divider
between two integers n, m.
T 20.1 If x is a nontrivial solution of x
2
= 1 mod N , then either
GCD(x − 1, N ) or GCD(x + 1, N ) is a factor of N ; such a factor is computable in
O
(L
2
) operations.
In the above, the two trivial solutions of x
2
= 1modN to be discarded are x =
±1modN corresponding to x = 1 and x =N −1. By assumption, therefore, the solution
x is in the range 1 < x < N − 1. We have x
2
− 1 = 0modN, which shows that N
divides by x
2
− 1 = (x + 1)(x − 1), or, equivalently, that N has a common factor with
either x − 1 or x + 1. We note that such a common factor cannot be N itself, since
x − 1 < x + 1 < N . Thus the factor is found by computing both GCD(x − 1, N ) and
GCD(x + 1, N ).
I shall now illustrate Theorem 1 through two basic examples.
11
See http://mathworld.wolfram.com/RSANumber.html.

20.4 From order finding to factorization 413
Table 20.3 Values of x
2
= z mod N for N = 35 and 1 < x < N − 1.
xzxzxzxzxz
1 8 29 15 15 22 29 29 1
2 4 911161123 43025
3 9 10 30 17 9 24 16 31 16
4 16 11 16 18 9 25 30 32 9
5 25 12 4 19 11 26 11 33 4
6113 29 20 15 27 29 34
71414212121281435
As a first example, assume the composite number N = 35. The values of x
2
=
z mod 35 are listed in Table 20.3. We observe from the table that x
2
= 1 mod 35 has two
nontrivial solutions x
1
= 6 and x
2
= 29 ≡−6 mod 35, or, equivalently, x =±6mod
35. With the solution x
1
= 6, we obtain GCD(x
1
− 1, N ) = GCD(5, 35) ≡ 5 and
GCD(x
1
+ 1, N ) = GCD(7, 35) ≡ 7. With the other equivalent solution x
2
= 29, we
obtain GCD(x
2
− 1, N ) = GCD(28, 35) = 7 and GCD(x
2
+ 1, N ) = GCD(30, 35) ≡
5. Thus, any of the solutions yield two GCDs that are both factors of N = 35.
As a second example, assume the composite number N = 561. With a tabulating
spreadsheet, we find the solutions x
2
= 1 mod 561 to be x
1
= 67, x
2
= 188, x
3
= 254,
x
4
= 307, x
5
= 373, and x
6
= 494, or, equivalently, x =±67, ±188, ±254. We can find
GCD(x
i
± 1, N ) by means of the extended Euclidian algorithm.
12
Given two numbers
a, b such that a > b, the algorithm can be summarized through the iterated operation:
(a, b) → (a
, b
) = (b, a mod b), (20.28)
which at the stage where b
= 0 yields a
= GCD(a,b). Let us illustrate the algorithm
through a basic example. Considering a = 561 and b = 189 for instance, we obtain the
following iteration:
(561, 189) → (a
, b
) = (189, 183)
(189, 183) → (a
, b
) = (183, 6)
(183, 6) → (a
, b
) = (6, 3)
(6, 3) → (a
, b
) = (3, 0).
The result obtained in the final iteration (where b
= 0) shows that GCD(561, 189) = 3.
Using the algorithm and a computing spreadsheet, we easily obtain for the solutions
x
1
, x
2
, x
3
:
GCD(x
1
− 1, N ) = GCD(66, 561) ≡ 33
GCD(x
1
+ 1, N ) = GCD(68, 561) ≡ 17
GCD(x
2
− 1, N ) = GCD(187, 561) ≡ 187
GCD(x
2
+ 1, N ) = GCD(189, 561) ≡ 3
GCD(x
3
− 1, N ) = GCD(253, 561) ≡ 11
GCD(x
3
+ 1, N ) = GCD(255, 561) ≡ 51.
12
See, for instance: http://en.wikipedia.org/wiki/Euclidean_algorithm.

414 Shor’s factorization algorithm
It is readily checked that 561 = 33 ×17 = 3 ×187 = 11 ×51 ≡ 3 ×11 ×17, which
shows that GCD(x
i
± 1, N ) is always a factor of N . We also observe that given a single
solution x
i
, one of the two corresponding GCD, i.e., GCD(x
i
± 1, N ), is a prime factor
of N (namely, 3, 11, or 17). The calculation of the six GCDs corresponding to the three
solutions x
1
, x
2
, x
3
, namely, GCD(x
1
± 1, N ), GCD(x
2
± 1, N ), and GCD(x
3
± 1, N ),
thus, makes it possible to factorize N completely.
The lesson learnt from Theorem 1 and these two illustrative examples is that the
knowledge of any single (nontrivial) solution of x
2
= 1modN yields two factors of N .
The complete factorization of N can, thus, be achieved by repeating the process with the
remaining factors (call any of these N
), provided that for each we can find a solution
of x
2
= 1modN
. What is the computation cost of the algorithm used to determine the
GCDs? There exist several possible answers to this question, depending on the algorithm
choice and its implementation. It can be shown that for L digit numbers, the extended
Euclidian algorithm complexity is of the order of O(L
2
) or better and, furthermore, that
there exist other algorithms for which finding the GCD is reduced to O[L(ln L)
2
ln ln L].
The continued fraction expansion algorithm, which was described in Section 20.3, can
be also implemented for this purpose but, as we have seen, its complexity is O(L
3
). Here,
we may only retain that finding the GCD through the extended Euclidian algorithm is,
at most, of the order of O(L
2
).
While Theorem 1 enables one to factorize a given composite number N rapidly, it
exclusively relies on prior knowledge of at least one nontrivial solution of x
2
= 1modN.
But how can we get this knowledge? This is where the order-finding algorithm, which
was described in Section 20.2, nicely comes to the rescue. As we have seen, given
any integer x, such that 1 ≤ x ≤ N − 1, the order of x modulo N is the smallest
number r for which x
r
= 1modN. In the case where r is even,lety = x
r/2
. We, thus,
have y
2
= 1modN, which shows that y is a solution of the Theorem 1 equation. If
y =±1modN , then y is a nontrivial solution of the equation and, according to the
theorem, GCD(y ± 1, N ) = GCD(x
r/2
± 1, N ) is a factor of N . In this case, the order-
finding algorithm successfully yields a determination of a factor of N.Ify is a trivial
solution, the algorithm fails, and the order-finding algorithm must be implemented again,
using a different trial value for x. The same conclusion applies when r turns out to be
odd. The fact that the algorithm may fail should not be perceived as an embarrassing
weakness of the factoring endeavor. It just takes a finite number of order-finding trials
(each of O(L
3
)) to lead to a successful and conclusive step, and as many such trials
to eventually achieve the full factorization. Actually, a second theorem shows that the
convergence of the algorithm is strong. This theorem states:
T 20.2 Given N, an odd composite integer with the factorization N =
p
α
1
1
p
α
2
2
... p
α
k
m
, where p
i
are prime numbers (α
i
integers), and given an integer x chosen
at random in the interval
[
1, N − 1
]
and co-prime to N, the probability that r is even
and y = x
r/2
is a nontrivial solution of y
2
= 1modN satisfies
p ≥ 1 −
1
2
m
. (20.29)

20.5 Shor’s factorization algorithm 415
This second theorem shows that the probability of successfully obtaining a factor of N
rapidly increases with the number m of prime factors. In the most basic case m = 2(asin
the above-described RSA challenge), we have p ≥ 1 − 1/2
2
= 0.75. This corresponds
to a 25% probability of failure, which reduces to less than 0.5% in four successive
trials! Since any composite is at least the factor of two primes, this failure probability
actually represents an upper bound for all possible composites. Theorem 2 is also a
very strong one: to implement the order-finding algorithm and find the factors of N if
successful, we are allowed to choose at random any integer x, provided it be co-prime
to N . The test is only a matter of calculating GCD(x, N ), at a mere
O
(L
2
) cost. It is an
academic issue to prove Theorem 2, which I shall not address here. The key lesson learnt
is that the order-finding algorithm leads to efficient and rapid factorization of composite
numbers. Basically, this whole description constitutes the essence and ingredients of
Shor’s factorization algorithm, to be summarized and illustrated in the next section.
20.5 Shor’s factorization algorithm
The rewards of going through the preceding sections and tedious developments are now
at hand. In fact, this section does not bring any new concept in this respect. It only consists
in the formalization of Shor’s factorization algorithm. There are many possible ways
to formalize an algorithm, from a list of practical steps with programming flow charts,
to more mathematically abstract and academic definitions. Here, I shall follow the first
approach and also provide some illustrations. It is brought to the reader’s attention that to
date, there exists no classical computer algorithm making it possible to implement order-
finding in polynomial time. The order-finding algorithm, the key constituent in Shor’s
factorization, is to be implemented in a hypothetical quantum-computing or quantum-
phase-estimation circuit, as illustrated in Fig. 20.3. As we have seen, the rest is only a
matter of classical computation with an overall
O
(L
3
)or
O
[(log N)
3
] complexity.
We may first make a few assumptions to simplify the algorithm description. First,
the composite number N must be odd. The test is immediate, based on the value
of the last or lowest-weight binary digit. Second, it must not be a trivial product of
small prime numbers and their powers. For instance N = 15, 27, 39, 144 are trivial
composites for the human brain. For a supercomputer, which has in its memory the list
of the first 1000 prime numbers (for instance), and look-up tables of the type shown
in Table 20.2 giving the basic factorizations, thereof, there exist millions of “trivial”
composites that can be factorized in milliseconds or faster. In such cases, there is no
point whatsoever in considering Shor’s algorithm! Another trivial case (as viewed from
a computer perspective) is when there exist two integers a ≥ 1 and b ≥ 2, such that
N = a
b
. It is an academic issue, not addressed here, to establish that the solution a, b
can be classically obtained in
O
(L
3
) time. The problem is, thus, reduced to the factoring
of a. It can be assumed that given N , all of the above tests, forming a “preamble” prove
negative, and this is where Shor’s algorithm must be implemented, as described in the
following.
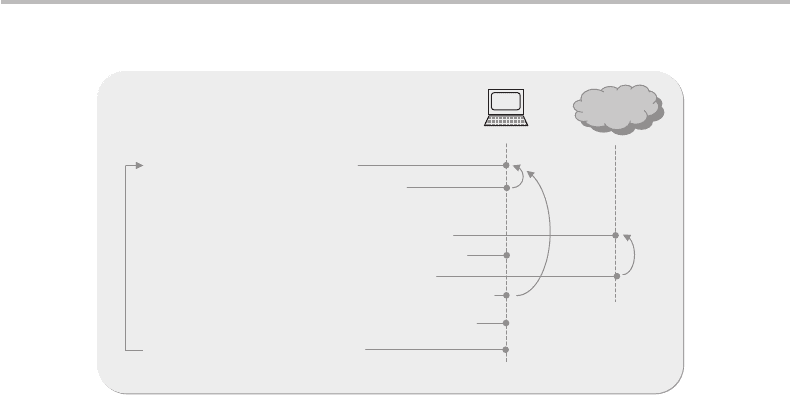
416 Shor’s factorization algorithm
quantum
1- Randomly chose
STEP
[]
2,2 −∈
N
x
),( NxGCD
Calculate , and if , redo
1>
2- Find , the order of modulo
x
N
r
> Make measurement of quantum phase
'/'
~
rs=
ϕ
> Get through the continued fraction expansion of
ϕ
~
r
> Check that , and if not redo
N
x
r
mod
1
=
3- Calculate
> Check that is even and , if not go to 1
Nx
r
mod1
2
/
−≠
r
()
(
)
NyGCDNNyGCDN ,1",,1'
−
=+=
4- Factorize (as applicable)
",' NN
Figure 20.4 Step-by-step implementation of Shor’s algorithm for nontrivial composite number N
of bit size L, returning all factors of N
.
Shor’s algorithm
Here is a step-by-step description, which is also schematically illustrated in Fig. 20.4.
Step 1 Choose at random x ∈
[
2, N − 2
]
and test if x, N are co-prime. If the test fails,
then another x must be selected.
Step 2 Find r, the order of x modulo N . This is done through the quantum phase
measurement or estimation, ˜ϕ = s
/r
, and the continued fraction expansion
algorithm, which yields r
= r, as described in Section 20.3. We then check
that x
r
= 1modN. As we have seen, there exists a small yet finite probability
that this operation may fail, in which case this test is negative, and we may just
try another phase measurement to obtain a different phase estimate, ˜ϕ. Then we
must ensure that r is even, and also that y = x
r/2
=−1modN is a nontrivial
solution.
13
If the test is negative, the whole process may be restarted at Step 1
(Theorem 2 ensures, however, that the success probability is high).
Step 3 Calculate GCD(y ± 1, N ), which yields two factors of N , call them N
, N
.
Then N
, N
can be submitted to the aforementioned “preamble” tests, to
identify whether further factorizing through Shor’s algorithm may be warranted.
Step 4 As applicable, N
, N
may be factorized in turn, starting again from step 1.
According to the above rendition of Shor’s algorithm, the end result is a prime
decomposition of two factors of N, according to N = p
α
1
1
p
α
2
2
M. In the case where
M > 1, the “preamble” tests may be implemented for the possibility of trivial factoriza-
13
As a matter of fact, given r being even, the test x
r/2
= 1modN does not need to be performed, as this
condition is implicitly verified should x be selected from the interval
[
2, N − 1
]
,orx = 1. This is because
r is, by definition, the smallest integer verifying x
r
= 1modN . Since r is even, then r/2isaninteger.
Then if we had x
r/2
= 1modN with x = 1, the period of x would be r/2 and not r, which proves the
point.
