Desurvire E. Classical and Quantum Information Theory: An Introduction for the Telecom Scientist
Подождите немного. Документ загружается.


20.6 Factorizing
N
= 15 and other nontrivial composites 417
tion. As applicable, Shor’s algorithm may otherwise be called upon again to factorize
M, and so on until we obtain the full prime-factor decomposition N = p
α
1
1
p
α
2
2
... p
α
k
m
.
20.6 Factorizing
N
= 15 and other nontrivial composites
In this section, I shall consider illustrative examples of Shor’s factorization algorithm,
using nontrivial composite cases (the notion of trivial composites will be specified
further down). This will also show how one can simplify the inverse Fourier transform
operation (FT
+
) in the quantum phase-estimation circuit, and estimate the probability
distribution function of the phase measurement.
Assume, for instance, the composite number N = 15. We must set L =log
2
N =4
for the size of the second or target register, and for an error probability of at most
ε = 0.25, we must also set K = 2L + 1 +log
2
[2 + 1/(2ε)]=11 for the size of the
first or control register. Thus, M = 2
K
= 2
11
= 2048. We then select “at random” from
the interval [2, N − 2] the value x = 8, which meets the requirement of being co-prime
to N . The qubit tensor input to the phase-estimation circuit in Fig. 20.3 is |ψ
1
=
|0
⊗K
⊗|1,Eq.(20.18). After passing through the Hadamard gate, it is transformed
into (Eq. (20.19)):
|
ψ
2
=
1
√
M
M−1
j=0
|j⊗|1
=
1
√
2
13
(
|0+|1+|2+···+
|
M − 1
)
.
(20.30)
After application of the controlled-U
j
gate, we obtain the state (Eq. (20.20)):
|ψ
3
=
1
√
M
M−1
j=0
|j⊗|x
j
mod N
=
1
√
M
M−1
j=0
|j⊗|8
j
mod 15
=
1
√
M
|0|1+|1|8+|2|4+|3|2
+|4|1+|5|8+|6|4+|7|2
+|8|1+|9|8+|10|4+|11|2+···
=
1
√
M
(
|0+
|
4
+
|
8
+···
)
|1
+
(
|1+
|
5
+
|
9
+···
)
|
8
+
(
|2+
|
6
+
|
10
+···
)
|
4
+
(
|3+
|
7
+
|
11
+···
)
|2
.
(20.31)
The state
|
ψ
3
in Eq. (20.31) can also be put in the form:
|
ψ
3
=
|
u
1
⊗|1+
|
u
2
⊗
|
8
+
|
u
3
⊗
|
4
+
|
u
4
⊗|2, (20.32)
418 Shor’s factorization algorithm
k
0
512
1024
1536
2048 =
M
2047 =
M
− 1
p
(
k
)
0.25
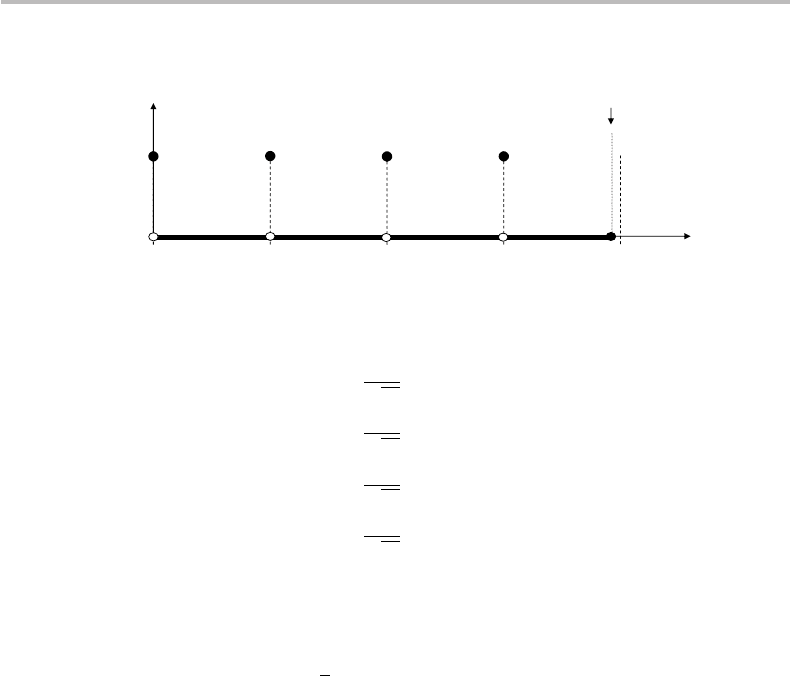
Figure 20.5 Plot of the distribution p(k) =|α
k
|
2
in the definition interval k ∈ [0, M − 1].
with
|
u
1
=
1
√
M
(
|0+
|
4
+
|
8
+···
)
|
u
2
=
1
√
M
(
|1+
|
5
+
|
9
+···
)
|
u
3
=
1
√
M
(
|2+
|
6
+
|
10
+···
)
|
u
4
=
1
√
M
(|3+
|
7
+
|
11
+···).
(20.33)
If at this stage (➂ in Fig. 20.3) we perform a measurement of the second register, which
is no longer used, Eq. (20.32) shows that we may obtain at random any of the values
z = 1, 8, 4, or 2, with a uniform probability of 1/4. Such a measurement causes the
first register to collapse into the corresponding state
|
u
1
,
|
u
2
,
|
u
3
,or
|
u
4
withanew
normalization factor of 1/
√
4. We could also make the same measurement at ➃, namely,
after the first register has been submitted to the inverse Fourier transform, FT
+
, and even
further down in the circuit, i.e., after the first register has been measured. Intuitively, the
measurement statistics of the second register are not affected by the transformation and
measurement of the first register, and the reverse. This principle can be stated as “any
quantum wires whose qubits are not measured at the end of a quantum circuit may yet
be assumed to be also measured, without affecting any other measurement statistics.”
It remains a fine point to analyze this principle academically, but here we shall take
its validity for granted. Assume, then, that our measurement of the second register
would be z = 8 (any other value giving identical results as the conclusion). Thus, in
the first register, the input to the inverse Fourier transform circuit would be
|
u
2
.After
transformation, the first register output is
FT
+
|
u
2
=
M−1
k=0
α
k
|k, (20.34)
where p(k) =
|
α
k
|
2
represents the probability distribution of the final measurement of the
first register. The detailed computation of the distribution p(k) is given in Appendix S.
The resulting distribution is plotted in Fig. 20.5. As we see from the figure, the
distribution exhibits four equiprobable peaks (p
max
= 0.25) at the register locations
k = 0, 512, 1024, 1536, with any other measurement probabilities being zero. This

20.6 Factorizing
N
= 15 and other nontrivial composites 419
probability distribution represents the ideal measurement conditions with zero failure.
As we have learnt, the actual measurement is successful only within some error proba-
bility ε, which is a function of the register size K , and which has been set in this example
to ε = 0.25. To recall, this failure probability can be made as small as desired, hence
making the measurement reality closer to the ideal probability distribution shown in Fig.
20.5. The existence of four equiprobable probability peaks betrays the periodicity of the
function x
n
mod N , which is of the order r = 4. But the experimentalist has no precon-
ceived idea of this, and is allowed to make only a few measurement attempts. Then it is
equally likely for each of the measurements to hit the values k
i
= 0, 512, 1024, or 1536.
To recall, these measurements correspond to the phase ˜ϕ ≈ ϕ = s/r, with 0 ≤ ϕ ≤ 1
being defined in K bits. The measurement, thus, corresponds to the rational numbers
k
i
/M = k
i
/2
K
= k
i
/2
13
= k
i
/2048, corresponding to the four possible determinations
˜ϕ:
0
2048
+
+
+
+
k
i
=0
,
512
2048
+
+
+
+
k
i
=512
,
1024
2048
+
+
+
+
k
i
=1024
,
1536
2048
+
+
+
+
k
i
=1536
.
The first determination, k
i
= 0, does not give any clue as to the order r. Measur-
ing it is, therefore, a failed attempt. Consider the next two other determinations, i.e.,
k
i
= 512, 1024. We have k
1
= 512/2048 = 1/4 and k
2
= 1024/2048 = 1/2. These two
rational numbers do not meet the condition in Eq. (20.25) since (1, 4) and (1, 2) are not
co-prime. Therefore, they cannot be convergent on ϕ. The last possible measurement,
k
3
= 1536 lends itself to the continued fraction expansion:
k
3
=
1536
2048
=
1
1 +
1
3
,
which, according to the algorithm (see Appendix R) gives the series of fractions p
0
/q
0
=
0/1, p
1
/q
1
= 1/1, and p
2
/q
2
= 3/4. Since (3, 4) are co-prime, the fraction 3/4 is a
convergent of ϕ and thus r = q
2
= 4 is of the order of x. Luckily, r = 4 is even,
and, furthermore, we have x
r/2
mod N = 8
2
mod 15 = 4 mod 15 =±1 mod 15, which
shows that the solution x
r/2
= 8
2
= 64 is valid (it can also be checked that x
r
= 8
4
=
1 mod 15, but this test does not need to be made). Therefore, two factors N
, N
of
N = 15 are
N
= GCD(x
r/2
− 1, N ) = GCD(63, 15) ≡ 3,
N
= GCD(x
r/2
+ 1, N ) = GCD(65, 15) ≡ 5,
which concludes Shor’s factorization algorithm. Since both factors N
, N
are prime,
the factorization of N is also complete! As we have seen, however, the algorithm
succeeded in this example because (a) one of the four possible measurements yielded
a valid convergent of ϕ, (b) the order r turned out to be even, and (c) the condition
x
r/2
=−1 mod 15 was satisfied. In the case where any of these prerequisites is not met,
the algorithm would have failed. Provided we obtained a convergent of ϕ, it turned out
that the random selection x = 8 was a “lucky” one. Then what are the other alternatives

420 Shor’s factorization algorithm
Table 20.4 Possibilities of selecting x towards the factorization
of N = 15 through Shor’s algorithm, with corresponding order
r,testx
r/2
=±1modN, and number m of convergents.
xrx
r/2
mod Nm
24 4 1
42 4 0
74 4 1
84 4 1
11211 0
13 4 4 1
and chances of failure under any other random selection for x? The answer is provided
in the following discussion.
Discussion
To factorize N = 15, we must randomly select x in the interval x ∈ [2, N − 2], with
the condition that (x, N ) be co-prime. This leaves x = 2, 4, 7, 8, 11, 13 as the only six
possibilities of fully implementing the algorithm. We then use a computer spread-
sheet to obtain the order r “classically” (this being not part of Shor’s algorithm,
but just a computing means for the purpose of the analysis). The results are listed
in Table 20.4, along with the test x
r/2
mod N and the number m of convergents.
It is seen from the table that the order of x is either r = 2(x = 4, 11) or r = 4
(x = 2, 7, 8, 13), and that both pass the test x
r/2
=±1modN . Consider the case
r = 4, and assume the register size K = 2
11
= 2048 (L = 4 bits). This case is wholly
identical to the previously described example where x = 8 was assumed. Then if we
implement Shor’s algorithm (namely without any prior knowledge of r), we have equal
probabilities of measuring k = 0, 512, 1024, 1536, corresponding to the determinations
˜ϕ = 0/2048, 512/2048, 1024/2048, 1536/2048. As we have seen, only the fourth one,
˜ϕ = 1536/2048 = 3/4, is a convergent of ϕ. Thus, only one measurement in four pos-
sibilities leads to a successful answer. If, on the other hand, our random selection is
x = 4, 11, the probability distribution has only two peaks corresponding to the determi-
nations ˜ϕ = 0/2048 and ˜ϕ = 1024/2048 = 1/2. Since none is a convergent of ϕ,the
algorithm fails, and we must try it again with a different value of x. To summarize,
the chances of randomly selecting the lucky values x = 2, 7, 8, 13 out of N − 3 = 12
possibilities in the interval x = [2, N − 2] are p
(1)
1
= 4/12 = 1/3, and the chances that
the output measurement leads to a convergent are p
(1)
2
= 1/4. On the other hand, the
chances of randomly selecting the “unlucky” values x = 4, 11 are p
(1)
1
= 2/12 = 1/6,
and the chances that the output measurement leads to a convergent are p
(1)
2
= 0. Over-
all, the chances of the algorithm concluding successfully in a single run, based on any
random selection of x are given by the probability indicator
=
2
i=1
p
(i)
1
p
(i)
2
= p
(1)
1
p
(1)
2
+ p
(2)
1
p
(2)
2
, (20.35)

20.6 Factorizing
N
= 15 and other nontrivial composites 421
Table 20.5 First group of composite numbers
N
=
pq
(
p
,
q
= 3, 5, 7, . . . , 37) eligible for factorization,
up to
N
= 1147, eliminating
N
=
a
b
(as shaded).
35711131719232931 37
3 9152133395157698793111
5
25 35 55 65 85 95 115 145 155 185
7
49 77 91 119 133 161 203 217 259
11
121 143 187 209 253 319 341 407
13
169 221 247 299 377 403 481
17
289 323 391 493 527 629
19
361 437 551 589 703
23
529 667 713 851
29
841 899 1073
31
961 1147
37
1369
which gives here = (1/3) ×(1/4) +0 ≡ 1/12 = 8.3%. But the discussion does not
end here. Indeed, this result actually assumes that the initial phase estimation ˜ϕ is
infinitely accurate (ε 1). As we chose K = 2L + 1 +log
2
[2 + 1/(2ε)]=11, cor-
responding to an estimation success of at least p = 1 −ε = 3/4, the overall success
chances in these global conditions are finally p = (3/4) ×(1/12) = 1/16 = 6.2%.
As the register size K is increased, the chances of success asymptotically reach the
limit . The key conclusion of this discussion is that, regardless of register size, the
implementation of Shor’s algorithm is a trial and error process: some values of x do not
work out, and in the best case, some register measurements fail to yield any convergent,
as we have seen with the N = 15 factorization example.
This discussion leads to another question: are some composites easier to factorize
than others under Shor’s algorithm, corresponding to higher values of the indi-
cator? In an attempt to address this question, we may analyze the periods of the
first composite numbers and see which ones may present the least factoring diffi-
culty or the highest . Consider, then, the composites of the type N = pq (with
p, q primes), which satisfy the two conditions: (a) N is not even, and (b) there are
no integers a, b (a, b ≥ 2), such that N = a
b
. With a list of the first primes limited
to p, q ={3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37}, excluding p, q = 2, the set of eligible
composites comes to 55 numbers ranging from N = 15 to N = 1147, as illustrated
in Table 20.5. The selection listed in the table, thus, justifies that N = 15 is the first
composite candidate to implement Shor’s algorithm. Considering the highest number
of the selection, N = 1147, determining the period would require one to compute
the successive powers of 1145
p
, which scale as 10
p×ln(1145)/ ln(10)
≈ 10
3p
and, thus,
rapidly leads to an overflow. If, on the other hand, we limit the scope to N ≤ 100, i.e.,
max(N ) = 91, the computation remains tractable (89
p
≈ 10
1.9p
), at least with a personal
computer. A period-finding computer program can easily be implemented,
14
yielding a
tabulation of r for each value x ∈ [2, N − 2], along with the validation tests {x
r/2
even
14
A free executable for period finding (FINDPRIM.EXE) can also be downloaded from: http://users.
pandora.be/nicvroom/progrm19.htm.
422 Shor’s factorization algorithm
=
N
15
21
33
35
39
0
2
4
2345678910111213
0
5
10
2 3 4 5 6 7 8 9 10111213141516171819202122232425262728293031
0
6
12
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33
0
6
12
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37
0
2
4
6
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
x
r
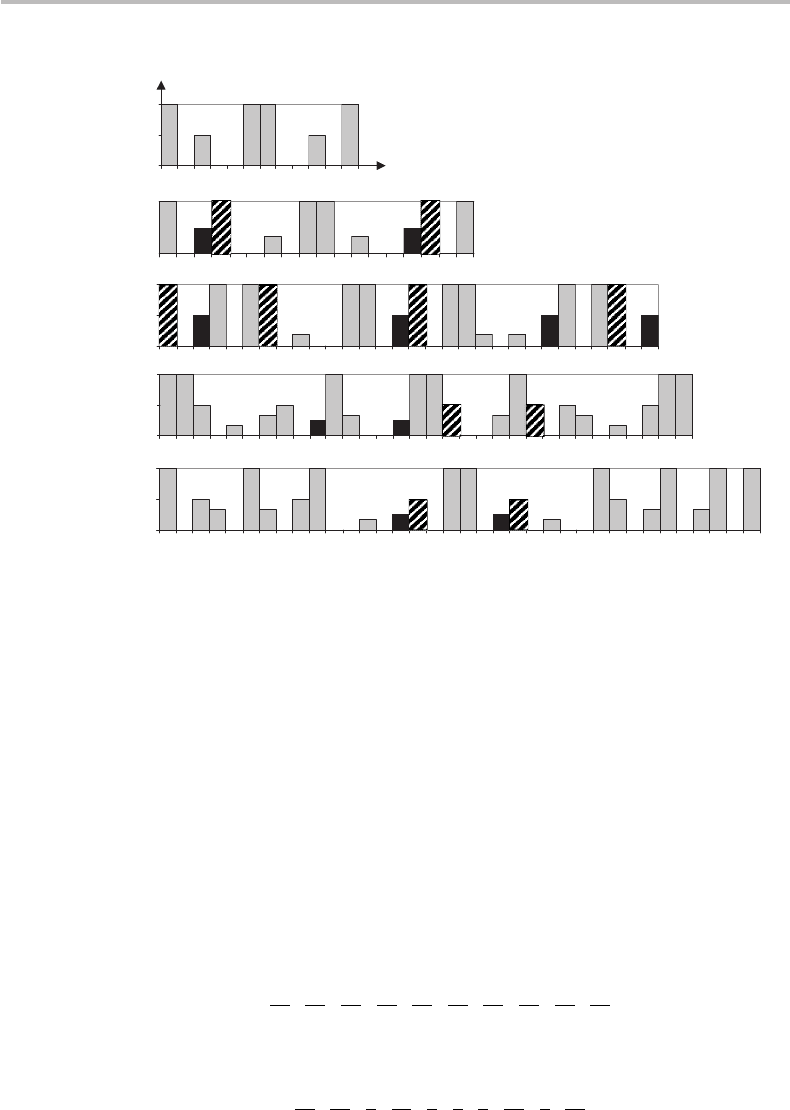
Figure 20.6 Va lu es r of the order of x modulo N (x, N co-prime) for composites
N = 15, 21, 33, 35, 39. The hashed bars correspond to odd values of r, the shaded bars
correspond to r values for which x
r/2
=−1 mod N.
and x
r/2
=±1modN }. The results for N = 15, 21, 33, 35, 39 are shown in Fig. 20.6.
The darkened data correspond to odd values of r, while the shaded data correspond to r
values for which x
r/2
=−1modN . The graph, thus, makes it possible to calculate the
probabilities p
(i)
1
, p
(i)
2
for each subset of x satisfying the algorithm requirements, and the
indicator =
i
p
(i)
1
p
(i)
2
. In the case N = 21, for instance, we find x ={2, 10, 11, 19}
for r = 6 and x ={8, 13} for r = 2, corresponding to p
(1)
1
= 4/18 = 2/9 and p
(1)
2
=
2/18 = 1/9, respectively. The associated values of r give p
(1)
2
= 1/3 and p
(2)
2
= 0,
respectively, yielding =(2/9) ×(1/3) + 0 ≡ 2/27 = 7.4% .
Considering next the case N = 33, we find x =
{
5, 7, 13, 14, 19, 20, 26, 28
}
for r =
10, x =
{
10, 21, 23
}
for r = 2, corresponding to p
(1)
1
= 8/30 = 4/15 and p
(2)
1
= 3/30 =
1/10, respectively. For r = 10, the probability distribution exhibits 10 peaks at the k
locations:
0
10
,
1
10
,
2
10
,
3
10
,
4
10
,
5
10
,
6
10
,
7
10
,
8
10
,
9
10
,
corresponding to the irreducible fractions p/q
0
10
,
1
10
,
1
5
,
3
10
,
2
5
,
1
2
,
3
5
,
7
10
,
4
5
,
9
10
,
in which only six have p, q as co-prime numbers. We, thus, have p
(1)
2
= 6/10 = 3/5
and also p
(2)
2
= 0, yielding = (4/15) ×(3/5) +0 ≡ 4/25 = 16.0%.
20.6 Factorizing
N
= 15 and other nontrivial composites 423
0.0
0.1
0.2
0.3
0.4
0.5
020406080100
Composite
N
(
N
)
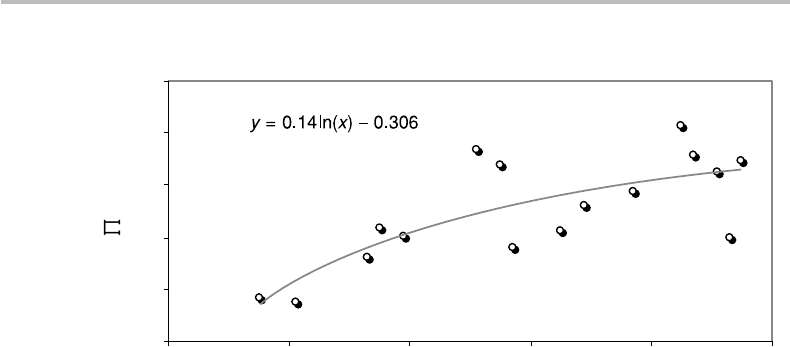
Figure 20.7 Indicator function (N ), corresponding to the probability of successfully factoring
N in a single run of Shor’s algorithm.
Similar analysis of the other N values leads to the indicator function (N ). To
recall, such a function represents the probability of successfully factorizing N based
on a single random selection of x ∈
[
2, N − 2
]
. The function (N) is plotted in
Fig. 20.7 for N ≤ 100. We observe from the plot that (N) increases with N accord-
ing to a logarithmic fit, along with some scattering. Such scattering is explained by
either “lucky” or “unlucky” composites. For instance, N = 15 and N = 51 are lucky
in the sense that all periods r satisfy the two conditions of being even and such that
x
r/2
= 1modN for any x ∈
[
2, N − 1
]
. This property maximizes the probability p
(i)
1
.
In contrast, for N = 93 (next to last point at right in Fig. 20.7) these conditions are not
met for 1/3 of all the possible r values, which explains the drop from the global trend.
Given an eligible r , and independently of N , the second “luck” factor comes from the
number of associated convergents, as measured by the probability p
(i)
2
. For instance,
r = 2 has no associated convergent, r = 4 has only one convergent with probabil-
ity p
(i)
2
= 1/4 = 25%, r = 10 has 6 convergents with probability p
(i)
2
= 6/10 = 60%,
and r = 28 has 24 convergents with probability p
(i)
2
= 24/28 = 85.7%. The product
p
(i)
1
p
(i)
2
, thus, determines the weight taken by a given period r out of the possibili-
ties indexed by i in the sum in Eq. (20.35) yielding (N ). For N ≤ 100, Fig. 20.7
shows that the maximum is found at N = 85 with (85) = 41.4%. The logarithmic fit
shown in the figure (y = 0.14 ln ×−0.306) suggests that a probability of = 50%
would be reached for x = 316, in the vicinity of the composites N = 319 = 11 ×29
and N = 323 = 17 ×19. As I am not aware that any plot similar to that shown in
Fig. 20.7 has ever been published. It remains a reasonable conjecture that for com-
posites larger than N = 100, (N ) asymptotically reaches 100%, with some scatter
due to the aforementioned effects, with the contribution of p
(i)
2
becoming negligi-
ble as N increases, as s, r in the phase estimate ϕ = s/r become more likely to be
co-prime.

424 Shor’s factorization algorithm
20.7 Public-key cryptography
This concluding section is about public-key cryptography (PKC). Such a topic is not
completely out of place in this chapter on Shor’s factorization algorithm because, as
I shall describe, the secrecy involved in PKC heavily relies on the fact that factoriz-
ing large numbers is a task that is essentially intractable, which is true according to
the best computing means and algorithms currently available. Since PKC is widely
used for different applications in the Internet, and since its principle is relatively sim-
ple to understand, it is worthwhile to describe it briefly here in the context of this
chapter.
Public-key cryptography was invented and developed by R. Rivest, A. Shamir and L.
Adleman, a trio of people who gave the name to the RSA standard. The RSA principle
feeds on the current fact that it is extremely difficult, if not completely intractable, to
factorize large composite numbers, or decompose them into a product of primes. Given
N , factorization (or prime decomposition) consists of finding the unique set of prime
numbers p
1
, p
2
,..., p
m
and powers α
1
,α
2
,...,α
m
such that p
α
1
1
p
α
2
2
... p
α
m
m
= N .For
instance, N = 1000 accepts the unique factorization or decomposition 2
3
× 5
3
= 1000.
For the purpose of PKC, we may just use two sufficiently large (and assumedly dif-
ferent!) prime numbers p, q to generate a “big” composite number N = pq,rest-
ing on the confidence that if anyone in the public domain knows N, that a person
or entity would have a hard time or find it impossible to figure out the two primes
p, q.
For instance, consider the number N = 62 615 533. To find its factorization, we need
to divide it by prime numbers, trying them out one after another. In this example, the
answer is p = 7919 and q = 7907, which are the highest two primes to be found at the
top of a list of the first thousands.
15
This unfortunate choice made the factorization easy,
since anyone can figure it out from such a list as representing the biggest product. What
about n = 15 773 077? The answer ( p = 2383, q = 6619) is less immediate, since it
takes 200 division tests to find q starting from the top of this first-thousand-prime list.
Assume next that p, q are selected from a huge list of known primes, for instance up to
10
9
, yielding composites N = pq up to the order of 10
18
.Evenatarateof10
9
division
tests per second (a state-class computing power that only a few may afford), this would
leave about 10
9
seconds or 31.7 years to find the prime factors!
I shall now focus on the RSA standard and algorithm specifics, after recalling the basic
underlying principle of cryptography. The principle of cryptography is to encode (or
encrypt) a given “open-text” message, called plaintext, into a “secret” message, called
ciphertext. Such words come from cryptology, the science, and history of cryptography,
16
15
For various lists of prime numbers, see, for instance: http://primes.utm.edu/lists/small/1000.txt, http://
en.wikipedia.org/wiki/List_of_prime_numbers; http://primes.utm.edu/; www.prime-numbers.org/; www.
rsok.com/∼jrm/printprimes.html.
16
For riveting and historical accounts of cryptology, see S. Singh, The Code Book (New York: Anchor Books,
1999), S. Levy, Crypto (Harmondsworth: Penguin Books, 2001), and D. Kahn, The Codebreakers, the
Story of Secret Writing (New York: Scribner, 1967). For an easy but detailed overview of crypto-algorithms

20.7 Public-key cryptography 425
whereby text messages were encrypted for the purposes of military, state, security, trade,
or simply private communications. In the computer age, however, any “text” to be so
encrypted may be anything from email to computer files, sensitive data, up to the payload
of Internet frames (as used in the so-called IPv6 standard or other secure-communication
protocols). Note that the word “cipher” indifferently designates the algorithm specifically
used for encryption, or the ciphertext material itself.
The destinee of the ciphertext (and only this person or entity), should be able to
make sense of it and translate it back into readable plaintext, an operation which is
called decryption. For this, he or she must use a secret key. By definition, the secret
key must be difficult to find or figure out, just like the combination of a bank safe, or a
“good” computer or network password.
17
Traditional cryptography, thus, requires that
the sender does communicate, by some indirect means, his or her key to the destinee,
so that the latter may be able to complete the decryption. In contrast, PKC came as a
revolution to this age-long principle by offering the possibility that the sender does not
know or use any secret key. Indeed, PKC is based on the “asymmetric” principle of using
two different cipher keys, one for encryption (public sender, call him Bob) and one for
decryption (individual destinee, call her Alice). I shall now describe how this puzzling
approach can make sense.
Define the two following keys:
r
For encryption: a number e, such that it is relatively prime with φ(N ) = (p − 1)
(q − 1);
r
For decryption: the number d, which satisfies ed = 1modφ,ord = e
−1
mod φ.
We shall call e the public key and d the private key. As its name indicates, the public
key should be available to anyone (Bob) who wants to send an encrypted message to
Alice. On the other side, Alice keeps her “private” key in absolute secrecy. The number
N = pq (also called the RSA modulus) is known or accessible to the general public,
Bob, or anyone else.
The operation of encryption with the public key e consists first of decomposing the
plaintext message into as many numerical blocks smaller than N . In the binary system,
a 64-bit block represents a maximum number of 1.8 ×10
19
, therefore, it is an eligible
block size if N ≥ 2 ×10
19
. For messages of arbitrary or random length, it is always
possible to “pad” the blocks with zeros on the left (called “nulls” in crypto jargon), so
that they fit a convenient standard size. Encryption of each of these blocks with number
value m is performed by calculating the (cipher) number
c = m
e
mod N . (20.36)
used from history to now, see E. Desurvire, Global Telecommunications, Broadband Access, Optical
Components and Networks, and Cryptography (New York: J. Wiley and Sons, 2004), Ch. 3, pp. 345–478,
from which this section on PKC is partially inspired. For an advanced description, see, for instance, B.
Schneier, Applied Cryptography (New York: J. Wiley and Sons, 2006).
17
If the key is easy or likely to be figured out by any third party, it is called a weak key.

426 Shor’s factorization algorithm
For Alice, who is the only one to own and know the private key d, the operation of
block-by-block decryption consists of computing
m
= c
d
mod N. (20.37)
Let’s now look at the modular-arithmetic value of the m
that Alice gets. It takes a few
substitutions to figure out that the result comes to:
m
= c
d
mod N
= (m
e
)
d
mod N
= m
ed
mod N
= m
k( p−1)(q−1)+1
mod N
= m × m
k( p−1)(q−1)
mod N
= m × [m
(p−1)(q−1)
mod N ]
k
mod N
= m × 1
k
mod N
= m.
(20.38)
The result in Eq. (20.38) shows that Alice has fully and unambiguously retrieved the
original plaintext block m. Note that for the above demonstration, we used different
properties of modular arithmetic, and in particular Euler’s theorem, as described in
Appendix T.
We also used the pre-set property of Alice’s key, ed = 1modφ, from which we have
ed = k( p − 1)(q − 1) +1. Alice is, thus, able to decrypt any message sent to her from
various “Bob” correspondents who may use her public key for this very purpose.
For illustration, consider a full example of RSA encryption and decryption.
18
First,
here is Bob’s private and intimate declaration to Alice:
Plaintext I l oveyou
PT-ASCII 1001001 1101100 1101111 1110110 1100101 1111001 1101111 1110101
Consistently with the RSA approach, Bob may encrypt his plaintext by blocks, which
represent for instance two letters each. With the above ASCII message, a two-letter block
is a number of 2 × 7 = 14 bits, corresponding to a maximum size of 2
14
–1= 16 383.
Let us assume that this is the standard. On her part, Alice also chose two primes p, q
whose product is greater or equal to 16 383, for instance p = 73 and q = 227, which
gives N =pq =16 571, and φ = ( p − 1)(q − 1) = 72 ×226 = 16 272. To be effective,
Alice made the number N = 16 571 known to everyone, just like a phone number in the
directory. Of course, the numbers p, q,φ remain only known to her.
18
This example was previously published in E. Desurvire, Global Telecommunications, Broadband Access,
Optical Components and Networks, and Cryptography (New York: J. Wiley and Sons, 2004).
