Desurvire E. Classical and Quantum Information Theory: An Introduction for the Telecom Scientist
Подождите немного. Документ загружается.

19.4 Grover quantum database search algorithm 397
0
1
H
ψ
ω
U
n
H
⊗
n
−
s
U
1
ψ
−
R
RG
G
s
−
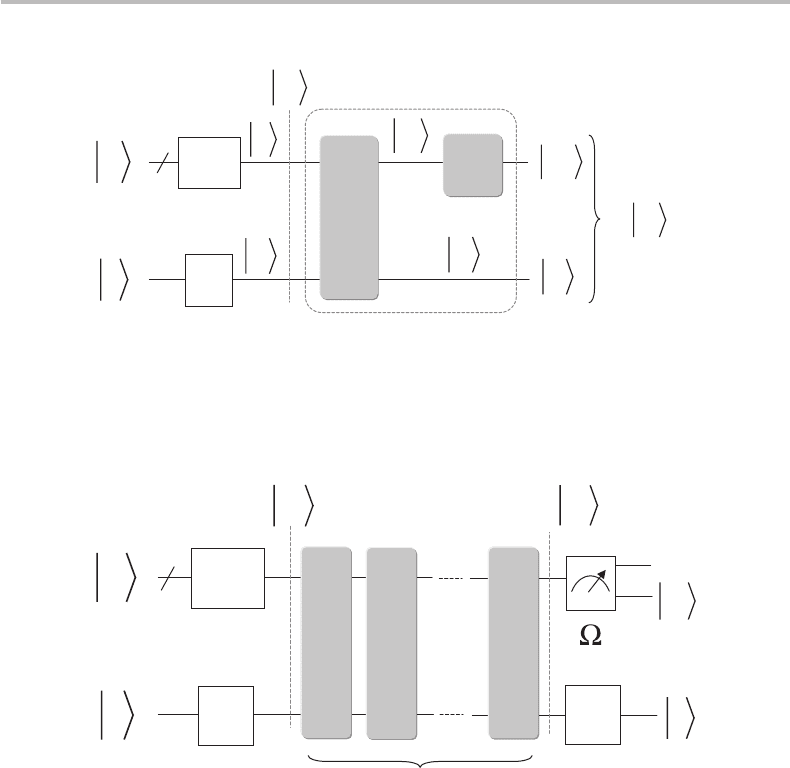
Figure 19.10 Quantum-gate circuit showing the initialization of the register state |R=|s|−
from n|0 ancilla qubit and one |1 ancilla qubit, and n + 1 Hadamard gates H . The circuit
shown in the dashed-line box is the iterative Grover operator G = U
s
U
ω
, with U
s
= 2|ss|−I .
0
1
H
G
n
H
⊗
n
1
R
G
G
max
k
H
RG
k
max
ω
λ
ω
times
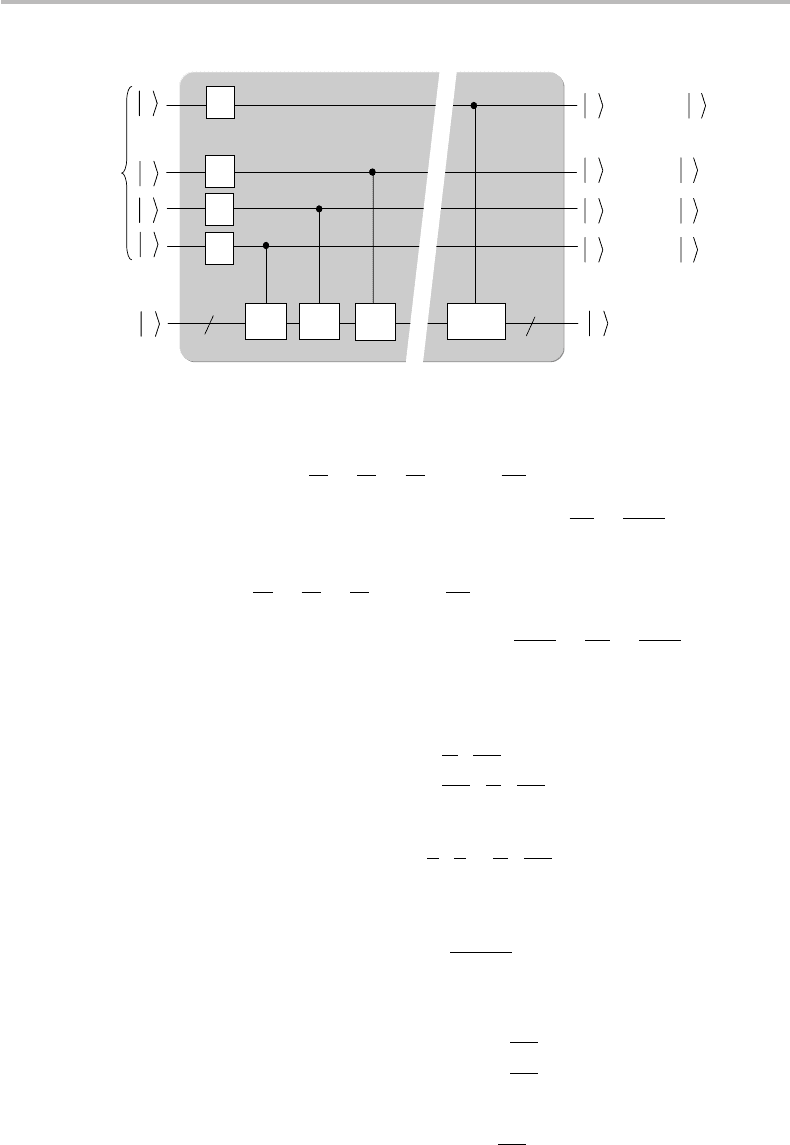
Figure 19.11 Quantum-gate circuit architecture for the full Grover quantum database search
algorithm implementation up to iteration k = k
max
showing eventual measurement of eigenvalue
λ
ω
through the observable (with success probability p(ω) ≈ 1).
The basic GQDS quantum-gate circuit architecture is shown in Fig. 19.10.From
the figure, we observe the initialization of the register state
|
R
=|s|− from n |0
ancilla qubits, one |1 ancilla qubit, and n + 1 Hadamard gates H . The circuit shown in
the dashed-line box is the iterative Grover operator G = U
s
U
ω
, with U
s
= 2|ss|−I ,
which now acts on the register state
|
R
=|s. It is only necessary to cascade the
Grover circuit G shown in Fig. 19.10 k
max
times to obtain the full GQDS circuit shown
in Fig. 19.11. As the figure shows, the algorithm implementation is complete with a
measurement (eigenvalue λ
ω
) of the observable with success probability p(ω) ≈ 1.
This description of the GQDS algorithm hopefully conveys the elegance of parallel
computing through quantum circuits. Yet there are many questions remaining on the
possible or even optimal circuit architectures for the “oracle” and Grover operators,

398 Quantum database search algorithms
let aside the practical physical implementation of the circuit at very large scales (N ≈
10
3
−10
9
), where the GQDS algorithm brings superior value. This reservation being
stated, in a rising twenty-first century dominated by Internet communications, with its
billions of host addresses, web pages, references, and databases, the physical possibility
of implementing GQDS algorithms through practical quantum computers would, beyond
any doubt, represent a most significant breakthrough. It would mean the possibility of
elaborate search algorithms over the Internet with relatively fast access times and, in
some applications, near-instantaneous access to practical information, however complex
or remote!
19.5 Exercises
19.1 (M): Show that for any n-qubit |x=
|
x
1
x
2
...x
n
, x
i
∈
{
0, 1
}
, and Hadamard
gate H ,wehave:
H
⊗n
|x=
1
√
2
n
z
(−1)
z·x
|z,
where
|
z
=
|
z
1
z
2
...z
n
and x · z = x
1
z
1
+ x
2
z
2
+···+x
n
z
n
is a scalar product
modulo 2.
19.2 (M): Given the orthonormal basis
{|
x
k
}
k=0...N −1
, show that the transformation
QFT, as defined by
|
y
n
=
1
√
N
N −1
k=0
e
i
k
2nπ
N
|x
k
,
is unitary.
19.3 (B): Calculate the quantum Fourier transform of the qubit:
|ψ=
1
√
14
|0+
2
i
√
14
|1+
3
√
14
|2.
19.4 (B): Calculate the quantum Fourier transform of four EPR–Bell states |β
00
,
|β
01
, |β
10
, |β
11
, as expressed in the ordered basis V ={|00, |01, |10, |11}.
19.5 (M): Given the definitions of G, |u, |ω, |s, and |ψ
1
=G|sin the text, demon-
strate by induction the result in Eq. (19.45) concerning the k action of the Grover
operator G on the state |s:
G
k
|s=cos
(
2k + 1
)
θ
2
|u+sin
(
2k + 1
)
θ
2
|ω.

20 Shor’s factorization algorithm
This chapter describes what is generally considered to be one of the most important and
historical contributions to the field of quantum computing, namely Shor’s factorization
algorithm. As its name indicates, this algorithm makes it possible to factorize numbers,
which consists in their decomposition into a unique product of prime numbers. Other
classical factorization algorithms previously developed have a complexity or computing
time that increases exponentially with the number size, making the task intractable if
not hopeless for large numbers. In contrast, Shor’s algorithm is able to factor a number
of any size in polynomial time, making the factorization problem tractable should a
quantum computer ever be realized in the future. Since Shor’s algorithm is based on
several nonintuitive properties and other mathematical subtleties, this chapter presents
a certain level of difficulty. With the previous chapters and tools readily assimilated,
and some patience in going through the different preliminary steps required, such a
difficulty is, however, quite surmountable. I have sought to make this description of
Shor’s algorithm as mathematically complete as possible and crack-free, while avoiding
some academic considerations that may not be deemed necessary from any engineering
perspective. Eventually, Shor’s algorithm is described in only a few basic instructions.
What is conceptually challenging is to grasp why it works so well, and also to feel
comfortable with the fact that its implementation actually takes a fair amount of trial and
error. The two preliminaries of Shor’s algorithm are the phase estimation and the related
order-finding algorithms. Both represent the purely quantum part of the approach: it
cannot be implemented classically. Basically, phase estimation allows one to find the
periodicity r of a modular function by means of a multi-qubit quantum-gate circuit
(Hadamard, controlled-U gates, inverse-Fourier transform), followed by a probabilistic,
quantum-mechanical measurement of the resulting qubit state, which yields a phase esti-
mate ϕ. Order finding, from which the period r is determined with high probability and
(the measurement being successful) without ambiguity, represents a particular case of
quantum phase estimation. Such a determination eventually rests on the implementation
of continued fraction expansion, a classical algorithm that is straightforward to run with
a computer. The requirement for r to be the period is that the phase estimation ϕ = s/r,
with s an integer, is such that s, r are co-prime. Since this does not happen systematically,
there is a finite chance that the endeavor may fail. Any such event is not a failure of Shor’s
algorithm, but rather a call for another try in this specific implementation step. Such con-
ditions of trial and error leading to factorizing success may sound strange to engineers –
but they are really embedded in the algorithm game! The key feature to grasp is that the

400 Shor’s factorization algorithm
probability of such intermediate failures remains comparatively small, or innocuous for
computing logistics, and that the chances of success, after only a few trials in the worst of
all cases, are relatively high. As we shall see, all of the above steps are of polynomial-time
complexity. A comparison is made with nonpolynomial algorithms, such as the general
number field sieve (GNFS) approach, which is shown to require decades of CPU comput-
ing time to factorize numbers of 100-bits long! We then establish the connection between
order finding and factorization of composite (or nonprime) numbers by using two basic
theorems. The first theorem yields the two factors N
, N
of any given composite N such
that N = N
× N
, given the knowledge of the period. The second theorem establishes
that the probability of the period meeting certain eligibility criteria is at least 75% for
any composite. These two theorems combined validate and conclude Shor’s factorization
algorithm. The factorization of the composite N = 15 = 3 ×5 is found in textbooks as
the only illustrative example of Shor’s algorithm. Here, we shall investigate the whole
space of nontrivial composites N ≤ 100, as an emulation of the quantum computer. It
is possible to do this based on the fact that for such relatively small numbers, we can
compute (with a basic home computer) all the possibilities associated with each step
of Shor’s algorithm, namely what the period-finding quantum circuit should yield, and
the associated probabilities of success or failure. The result of this investigation is an
original plot showing the probability of successfully concluding the factorization of
nontrivial composites N ≤ 100 in a single run. The exercise helps one to grasp how
Shor’s algorithm would work when taking greater composite numbers. The last section,
which briefly describes public key cryptography (PKC), is not completely out of place in
this chapter. The purpose of this addition is to show how the PKC algorithm works, as
based on the product N = pq of two prime numbers p, q, whose factorization is indeed
considered intractable by classical means. Should a quantum computer of corresponding
computing power be implemented someday, the whole field of PKC-based cryptography,
and Internet security for that matter, would be compromised overnight! Fortunately, this
remains a distant perspective, while from this chapter, we know that the theory works
mathematically.
20.1 Phase estimation
This section considers an algorithm referred to as phase estimation. The word “esti-
mation” is correct, because the outcome of the algorithm is only what can be called a
good estimate of the phase in a quantum system. This phase estimation will enable us
to move another step further in our progression towards Shor’s factorization algorithm,
the second step being the order-finding algorithm, to be considered in the next section.
These two steps are critical in the final understanding of Shor’s algorithm, and this is
why we ought to pay extra attention to the following. While based on lessons from
previous chapters with no new conceptual difficulty, the quantum phase estimation and
its application to order finding involve a few nontrivial properties and results, which
must be fully assimilated at each step of the description.

20.1 Phase estimation 401
Assume a unitary operator U , with eigenstate |u of dimension L, and of unknown
complex eigenvalue λ
φ
= e
2
i
πϕ
, where ϕ is a real number such that 0 ≤ ϕ ≤ 1,
is to be determined through the aforementioned “phase estimation” algorithm. Also
assume that we are capable of building a family of controlled-U
p
operators, where
p = 2
0
, 2
1
,...,2
K −1
is any power of two up to K − 1. The phase-estimation (PE) cir-
cuit comes in two stages, which we shall call here “front-end” and “back-end” modules,
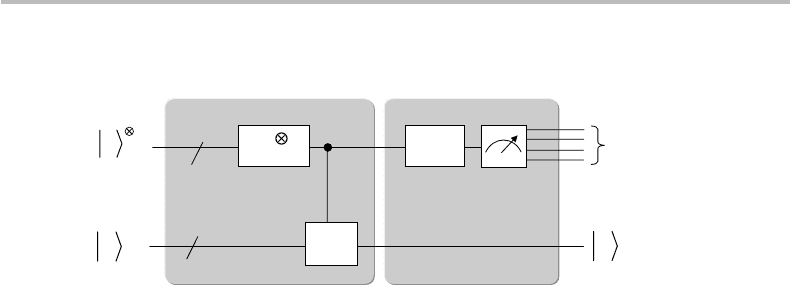
respectively. The PE front-end module is shown in Fig. 20.1. As we observe, its embod-
iment includes an input register of K ancilla qubits |0, and the eigenstate |u, which is
an L-qubit. Each of the qubits in the input register is submitted to a Hadamard transform
(H ), the output of which drives an individual controlled-U
p
gate, according to the array
sequence shown at the bottom of the figure. It is easily established that the output register
consists of K qubits of the form |0+
e
2
i
π pφ
|1 with p = 2
0
, 2
1
,...,2
K −1
and leaves
invariant the L-qubit |u, as indicated in Fig. 20.1.
1
The tensor-product output can also
be rewritten as a sum of K + L qubits of the form
e
2
i
πkϕ
|k⊗|u:
2
1
2
K /2
|0+
e
2
i
π2
K −1
ϕ
|1
|0+
e
2
i
π2
K −2
ϕ
|1
...
|0+
e
2
i
π2
1
ϕ
|1
×
|0+
e
2
i
π2
0
ϕ
|1
⊗|u=
1
√
N
N −1
k=0
e
2
i
πkϕ
|k⊗|u,
(20.1)
with N = 2
K
. This result, in the summation form, will be used later. We shall now
interpret the product form. Recall that ϕ is a real number, such that 0 ≤ ϕ ≤ 1. Any
such number can be represented in binary form, which is noted ϕ = 0.ϕ
1
ϕ
2
ϕ
3
...ϕ
K
...,
according to the definition:
ϕ = 0.ϕ
1
ϕ
2
ϕ
3
...
=
ϕ
1
2
+
ϕ
2
4
+
ϕ
3
8
+···+
ϕ
K
2
K
+···,
(20.2)
1
To show this, consider the effect of a controlled-U
p
gate, noted CU
p
, at any stage in the circuit in
Fig. 20.1. In each gate, the control qubit is H|0=|0+|1, within the factor 1/
√
2. The tensor-product
output is CU
p
[(|0+|1) ⊗|u] or, identically, |0⊗|u+|1⊗U
p
|u=|0⊗|u+|1⊗e
2iπ pϕ
|u
≡ (|0⊗e
2iπ pϕ
|1) ⊗|u. Clearly, the first and second terms in this tensor product belong to the first
and second registers, respectively.
2
This is established by developing the tensor product in the left-hand side, starting from the last two terms
(or considering K = 2):
#
|0+e
2iπ2
1
ϕ
|1
$#
|0+e
2iπ2
0
ϕ
|1
$
=|0|0+|0e
2iπ2
0
ϕ
|1+e
2iπ2
1
ϕ
|1|0+e
2iπ2
1
ϕ
|1e
2iπ2
0
ϕ
|1
=
|
00
+ e
2iπ2
0
ϕ
|
01
+ e
2iπ2
1
ϕ
|
10
+ e
2iπ(2
1
+2
0
)ϕ
|
11
≡ e
2iπ0ϕ
|0+e
2iπ1ϕ
|1+e
2iπ2ϕ
|2+e
2iπ3ϕ
|3
=
3
k=0
e
2iπkϕ
|k,
noting that the tensor products |ij, with i, j = 0, 1, are noted |i × 2
0
+ j × 2
1
. It is clear that the full
product yields the summation shown in the right-hand side in Eq. (20.1).
402 Shor’s factorization algorithm
0
u
H
0
2
U
0
0
0
H
H
H
…
1
2
U
2
2
U
1
2
−
K
U
L
u
10
1
22
φπ
−
+
K
i
e
10
22
φπ
+
1
2
i
e
10
22
φπ
+
i
e
0
10
2
2
φπ
+
i
e
K
L
. . .
. . .
Figure 20.1 Quantum circuit for phase estimation (front-end module).
where ϕ
i
= 0, 1 are bits. In particular, we have
2
K −1
ϕ = 2
K −1
#
ϕ
1
2
+
ϕ
2
4
+
ϕ
3
8
+···+
ϕ
K
2
K
+···
$
={ϕ
1
2
K −2
+ ϕ
2
2
K −3
+···+ϕ
K −1
2
0
}+
ϕ
K
2
+
ϕ
K +1
4
+···
(20.3)
and
2
K −2
ϕ = 2
K −2
#
ϕ
1
2
+
ϕ
2
4
+
ϕ
3
8
+···+
ϕ
K
2
K
+···
$
={ϕ
1
2
K −3
+ ϕ
2
2
K −4
+···+ϕ
K −2
2
0
}+
ϕ
K −1
2
+
ϕ
K
4
+
ϕ
K +1
8
+···
(20.4)
Noting that the terms within braces
{}
in the right-hand side in Eqs. (20.3) and (20.4)
are integers, we have for the imaginary exponentials:
e
2
i
π2
K −1
ϕ
=
e
2
i
π
(
ϕ
K
2
+
ϕ
K +1
4
+···
)
e
2
i
π2
K −2
ϕ
=
e
2
i
π
(
ϕ
K −1
2
+
ϕ
K
4
+
ϕ
K +1
8
+···
)
.
.
.
e
2
i
π2
0
ϕ
=
e
2
i
π
#
ϕ
1
2
+
ϕ
2
4
+···
ϕ
K
2
K
+
ϕ
K +1
2
K +1
+···
$
.
(20.5)
Introduce the definition
m
=
m
l=1
ϕ
K −m+l
2
l
, (20.6)
and substitute it into Eq. (20.5) to obtain
e
2
i
π2
K −1
ϕ
=
e
2
i
π
1
e
2
i
π
(
ϕ
K +1
4
+···
)
e
2
i
π2
K −2
ϕ
=
e
2
i
π
2
e
2
i
π
(
ϕ
K +1
8
+···
)
.
.
.
e
2
i
π2
0
ϕ
=
e
2
i
π
K
e
2
i
π
#
ϕ
K +1
2
K +1
+···
$
.
(20.7)
We then consider the specific case where ϕ is exactly defined by K bits, meaning that
all bits ϕ
K +1
,ϕ
K +2
,... are identically zero. Substituting the results in Eq. (20.7) into

20.1 Phase estimation 403
Eq. (20.1) under this assumption, and overlooking the output qubit |u, yields the first
register output:
1
2
K /2
(|0+
e
2
i
π
1
|1) ⊗ (|0+
e
2
i
π
2
|1) ⊗···⊗(|0+
e
2
i
π
K
|1). (20.8)
As based on Eqs. (19.29) and (19.30), the result in Eq. (20.8), together with the definition
in Eq. (20.6), is immediately identified as being the quantum Fourier transform of the
“phase” qubit |ϕ=
|
ϕ
1
ϕ
2
...ϕ
K
. We can, thus, recover |ϕ, by performing the inverse
Fourier transform of the output register, followed by a measurement in the computational
basis, which yields the K classical bits ϕ
1
ϕ
2
...ϕ
K
defining the phase. The “back-end”
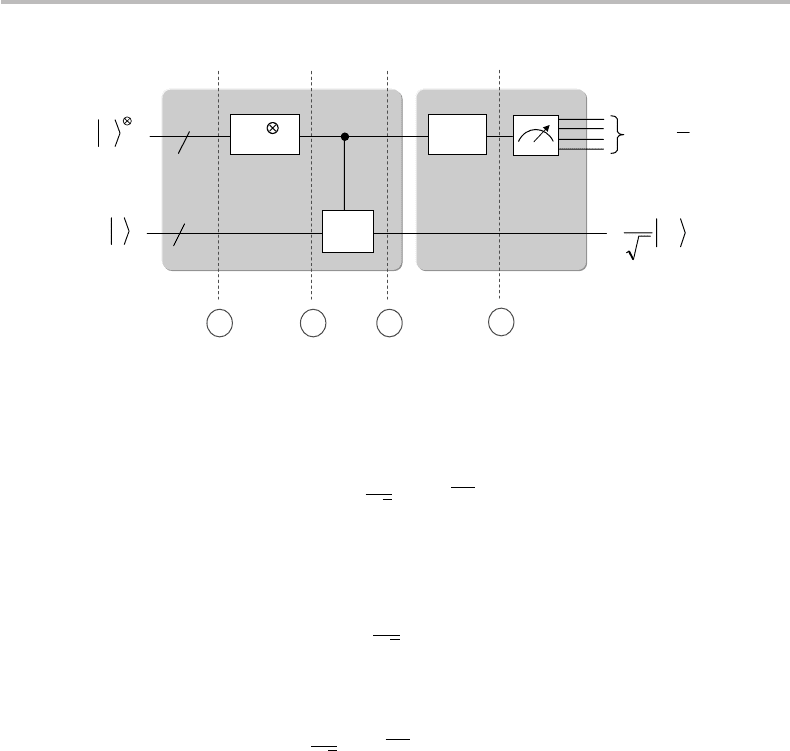
module of the PE circuit, thus, consists first of an inverse Fourier transform circuit, noted
FT
+
. This circuit is shown in Fig. 19.4, while conceived as being traversed from right
to left. The second component of the back-end module is a K -qubit measurement gate,
which restitutes the ϕ
1
ϕ
2
...ϕ
K
bits. The full PE circuit including front and back ends,
is represented schematically in Fig. 20.2, assuming that the phase ϕ is exactly defined
by K bits, or 2
K
ϕ is an integer.
Consider next the more general case where 2
K
ϕ is not an integer. Let us calculate the
state of the output register after the circuit shown in Fig. 20.2. Starting from the input
|0
⊗K
|u, and based on the result in Eq. (20.1) followed by the inverse Fourier transform,
we have the following state evolution:
|0
⊗K
|u→
1
√
N
N −1
k=0
e
2
i
πkϕ
|k|u
→
1
√
N
N −1
k=0
e
2
i
πkϕ
3
1
2
K /2
N −1
n=0
e
−
2
i
πkn
N
|
n
4
|u
=
1
N
N −1
n=0
N −1
k=0
e
−
2
i
πkn
N
e
2
i
πkϕ
|n|u
=
1
N
N −1
n=0
N −1
k=0
e
2
i
π(ϕ−
n
N
)
k
B
|n|u
=
1
N
N −1
n=0
1 −
e
2
i
π
(
ϕ−
n
N
)
N
1 −
e
2
i
π
(
ϕ−
n
N
)
B
|n|u.
(20.9)
The probability of measuring n from the output register (or the probability of the
N -qubit register being in state
|
n
) is given by the square modulus of the corresponding
amplitude, namely, from Eq. (20.9):
p(n) =
1
N
2
+
+
+
+
+
1 −
e
2
i
π
(
ϕ−
n
N
)
N
1 −
e
2
i
π
(
ϕ−
n
N
)
+
+
+
+
+
2
≡
1
N
2
sin
2
π
#
ϕ −
n
N
$
N
sin
2
π
#
ϕ −
n
N
$
.
(20.10)
404 Shor’s factorization algorithm
u
K
H
j
U
L
u
K
K
ϕ
ϕ
. . .
1
+
FT
K
0
(a) (b)
Figure 20.2 Full quantum circuit for phase estimation, with (a) front-end and (b) back-end
modules.
The measurement of n, with associated probability p(n), corresponds to the phase
estimation ˜ϕ = n/N . The probability is maximal when δ = ϕ − ˜ϕ is minimal. The
probability defined in Eq. (20.10) rapidly vanishes as the error δ departs from this
minimum. The conclusion is that the measurement has the highest probability of yielding
the closest approximation of the phase ϕ. Based on the results in Eqs. (20.9) and (20.10),
it is also established that the circuit output is of the form | ˜ϕ|u, where
|
˜ϕ
is a state
superposition which, when measured, yields a fair approximation of the phase ϕ.
It is an academic issue, which I shall not address here, to determine the size of K
required for obtaining a phase accuracy of 2
−l
(or l bits) with an arbitrary high probability
of success. Suffice it to provide the result of the analysis: for this probability to be at
least 1 −ε, the rule is that the control register size must be K = l +log
2
[2 + 1/(2ε)].
It is readily checked that the probability’s lower bound increases from 50% (ε = 0.5)
to 99% (ε = 0.01) and 99.9% (ε = 0.001) with K = l + 2, K = l + 6, and K = l + 9,
respectively, which illustrates the very rapid probability convergence with register size
K , given the desired number of bits accuracy, l.
The above phase-estimation algorithm requires one to prepare the eigenstate |uof the
operator U as the target register. What about the case where we have no prior knowledge
of this eigenstate? The remaining possibility is to input to the circuit some other N -qubit
|
ψ
, which we know how to prepare. This state can be uniquely decomposed over the
orthonormal eigenstate, basis
{
|u
}
, according to
|
ψ
=
u
c
u
|u. By the principle of
linearity of quantum gates, we then obtain for the circuit output |ψ
=
u
c
u
|
˜ϕ
u
⊗|u.
On measuring the first register, we obtain a fair estimation of the phase ϕ
u
, but this time
associated with one possible eigenstate |u, with measurement probability
|
c
u
|
2
. Such
a way to proceed, thus, yields a fair estimation of ϕ
u
from an unknown eigenstate
|u selected at random in the eigenstate basis. Stated without demonstration, but as
intuitively expected, the probability of success for a phase-estimation accuracy of 2
−l
(or l bits) is at least
|
c
u
|
2
(1 − ε) when the size register K is chosen according to this
rule.
The phase-estimation circuit, and, in particular, the “successful phase-approximation”
algorithm, including the case of unknown eigenstates, are the key to solving the so-called
order-finding problem, as we shall see in the next section.

20.2 Order finding 405
Table 20.1 Successive powers of x = 4 modulo N = 13, showing order r = 6.
p 4
p
4
p
mod 13 p 4
p
4
p
mod 13 p 4
p
4
p
mod 13
011 6 4 096 1 12 16 777 216 1
1 4 4 7 16 384 4 13 67 108 864 4
2 16 3 8 65 536 3 14 268 435 456 3
3 64 12 9 262 144 12 15 1 073 741 824 12
4 256 9 10 1 048 576 9 16 4 294 967 296 9
20.2 Order finding
In this section, I shall describe the order-finding algorithm, which is based on the concept
of number order in modular algebra. It will then be shown that there exists a unitary
operator U that allows one to determine this order through the previously described
phase-estimation circuit. Let us introduce the “order” concept first. In the foregoing, we
shall call M = 2
K
the number of Fourier components, and from now on use N as the
integer number that Shor’s algorithm will attempt later to factorize into prime numbers.
Assume, then, two positive integer numbers x, N , such that x < N , with the two
numbers having no common divisor other than unity. It is said that their greatest common
divisor (GCD) is unity, or equivalently, that the two numbers are co-prime. By definition,
the order of x modulo N is the smallest nonzero integer r satisfying
x
r
= 1modN. (20.11)
The order of x can also be conceived as the period of the powers x
0
, x
1
, x
2
..., modulo
M. To give an example, let x = 4 and N = 13. The successive powers of 4 modulo 13
are listed in Table 20.1. It is seen that the period of the power series is r = 6, which also
corresponds to the smallest nonzero integer for which 4
r
= 1 mod 13, according to the
order definition in Eq. (20.11).
Next, I shall describe how the quantum phase-estimation circuit makes it possible to
determine r, the order of x modulo N , with a high probability of success and accuracy. For
this, we first need to introduce the appropriate unitary operator U and its corresponding
eigenstates and eigenvalues. We assume that given two integers x, N , satisfying x < N
and x being co-prime to M, there exists some operator U
x,N
, which acts on the qubit
|y=|0, |1 as:
U
x,N
|y=|xy mod N . (20.12)
In the following, I shall just note U
x,N
= U for simplicity.
Second, let {|u
s
}
s=0,1...r−1
be the set of r eigenstates of U , with associated eigenvalues
exp(2
i
πs/r), namely, satisfying
U
|
u
s
=
e
2
i
πs
r
|
u
s
(20.13)
406 Shor’s factorization algorithm
K
H
j
U
L
K
r
s
s
=
ϕ
+
FT
K
0
1
1 2 3
4
s
u
r
1
Figure 20.3 Quantum circuit for order finding.
and with the phase ϕ
s
= s/r satisfying 0 ≤ ϕ
s
≤ 1. Such eigenstates are defined accord-
ing to
|
u
s
=
1
√
r
r−1
k=0
e
−
2
i
πks
r
|x
k
mod N , (20.14)
which is left as an easy exercise to prove. Finally, we shall observe that the above-defined
eigenstates
{|
u
s
}
satisfy the properties
1
√
r
r−1
s=0
|u
s
=|1 (20.15)
and
1
√
r
r−1
s=0
e
2
i
πks
r
|
u
s
=|x
k
mod N , (20.16)
which are also left as easy exercises to prove. The property in Eq. (20.15) is rather
convenient, since we do not know how to define the state
|
u
s
, which is a function of the
unknown parameter r to be estimated! Recall, indeed, from the previous section, that
if we do not know the eigenstate to input to the phase-estimation circuit, we can still
use an eigenstate superposition, here, namely, a known state |1 of some arbitrary qubit
dimension L. The nice additional feature is that the coefficients in the superposition
correspond to a uniform probability distribution p(s) =
|
c
s
|
2
= 1/r, for the register
measurement and phase estimation.
The next step will show that using |1 as the input to the second register of the phase-
estimation circuit yields, as the output of the front-end module, a K superposition of the
states |k⊗|x
k
mod N . The property in Eq. (20.16) then makes it possible by inverse
Fourier transform (back-end module) to obtain a fair estimation ˜ϕ
s
of the actual phase
ϕ
s
= s/r . Let us see now in detail how the state evolves step by step through the phase-
estimation circuit, which is represented in Fig. 20.3. We assume that the first, control,
and second, target, register sizes are K and L =log
2
N , respectively, with the relation
between the two to be specified later on. The controlled-U
j
gates perform the application
