Desurvire E. Classical and Quantum Information Theory: An Introduction for the Telecom Scientist
Подождите немного. Документ загружается.

18.5 Quantum teleportation 367
H
q
00
b
Bob
Alice
´
m
´
m
X
m
Z
m
1
2
3
4
q
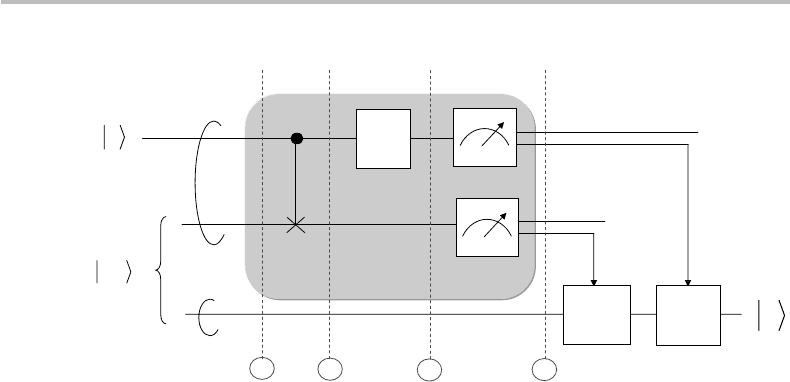
Figure 18.7 Circuit used by Alice and Bob for quantum teleportation.
18.5 Quantum teleportation
The strange technique referred to as quantum teleportation (QT) makes it possible to
transmit an unknown qubit instantaneously over any distance. Here, “distance” means
any range spanning from next door’s office to the opposite end of the Solar System, or
even beyond in the Universe, despite the limitations imposed by Einstein’s theory of
relativity, the physical finiteness of the speed of light, and its invariance regardless of
any reference frame.
To a wider audience, the word “teleportation” may raise false expectations in terms of
the capability of moving physical objects, which we may call here “macrosystems,” such
as a coin, a cat or a human being (see Chapter 15)! The expectations are high indeed
if public audiences “buy in” the quantum state superposition concept as applicable
to the macroscopic world. At a microscopic scale, however, the notions of QT and
“nonlocality” implications, are absolutely correct. Suffice it to recall here that in the
quantum world, any elementary object, such as an atom or a particle, is, to all intents and
purposes, a quantum system, and there are no conceptual limitations involved therein,
both in terms of locality and physical distance. As we shall see, however, there is
no contradiction between QT and relativity laws, when it comes to measuring actual
information.
In this book, QT is, thus, our first quantum algorithm to “transport” quantum states,
whose most elementary description is the qubit. The key to the QT algorithm is the
use of an EPR–Bell state (or ebit), as a resource commonly shared between Alice and
Bob, and making it possible for Alice to send any qubit to Bob. As we shall see,
teleportation also requires the communication of two classical bits (cbits), using any
classical communication channel, such as the telephone, or the Internet, for instance.
This preliminary observation is completely sufficient to justify that indeed, teleportation
does not violate relativity laws.
The principle of the generic QT circuit is illustrated in Fig. 18.7. As the figure shows,
this is a 3-qubit circuit, which includes a Bell-state measurement apparatus (as shaded),

368 Qubit measurements, coding, and teleportation
which outputs the two cbits m, m
, and two gates (X, Z), which are used according to
the powers of m, m
. The two top wires are connected to Alice’s side, while Bob uses
the bottom wire for final measurements. The qubit that Alice wants to transmit to Bob
is |q=α|0+β|1, as shown at top left. Alice and Bob also share the resource of an
EPR–Bell state, here, for instance, |β
00
. The end result of the QT is that Bob is able to
retrieve the qubit |q=α|0+β|1, as shown at bottom right. At first glance, this QT
circuit looks somewhat involved but, as we shall see, its operation turns out relatively
easy to grasp, should one proceed step by step using the corresponding numbers shown
in Fig. 18.7.
The initial state of the system, marked ➀,is|q⊗|β
00
, namely, using the simplified
3-qubit notation:
|q⊗|β
00
=(α|0+β|1) ⊗
1
√
2
(|00+|11)
≡
1
√
2
(α|000+α|011+β|100+β|111).
(18.20)
Next, we evaluate the system state at ➁. As seen from the figure, the CNOT gate
controls the second qubit from the first qubit, with the equivalent of the logical XOR,
i.e., |x, y, z #→|x, x ⊕ y, z. Hence, we have at ➁:
1
√
2
(α|000+α|011+β|100+β|111)
#→
1
√
2
(α|000+α|011+β|110+β|101).
(18.21)
Next, we evaluate the system state at ➂. The only change is the passing of the first
qubit through the Hadamard gate H. To recall, H|0=(|0+|1)/
√
2 and H |1=
(|0−|1)/
√
2. This transforms the 3-qubits in Eq. (18.20) according to the following
(the underline to stress the qubit being acted on):
|0
00 #→
1
√
2
(|0
00+|100)
|0
11 #→
1
√
2
(|0
11+|111)
|1
10 #→
1
√
2
(|0
10−|110)
|1
01 #→
1
√
2
(|0
01−|101).
(18.22)
Hence we have at ➂:
1
√
2
(α|000+α|011+β|110+β|101)
#→
1
2
{α|000+α|100+α|011+α|111+β|010−β|110+β|001−β|101}
≡
|00
α|0+β|1
2
+|01
α|1+β|0
2
+|10
α|0−β|1
2
+|11
α|1−β|0
2
%
.
(18.23)

18.5 Quantum teleportation 369
Table 18.3 State collapse resulting from Alice’s 2-qubit measurements
(m, m
), and corresponding gates X
m
Z
m
to be used by Bob in order to
retrieve the original qubit |q=α|0+β|1.
Alice measures
mm
Alice measures Bob’s 1-qubit X
m
Z
m
00 |00 α|0+β|1 I
01 |01 α|1+β|0 Z
10 |10 α|0−β|1 X
11 |11 α|1−β|0 XZ
In the last expression in the right-hand side, the first two qubits, which are controlled
by Alice, and the last qubit, which is Bob’s, have been regrouped for clarity. Then come
Alice’s measurements of the first two qubits, with the corresponding classical-bit results
m, m
(respectively) obtained at ➃. The rule has it that Alice must communicate the two
classical bits, or cbits, m, m
to Bob. It is clear that if Alice measures |00, the system
state collapses into the qubit |00(α|0+β|1), as shown in Eq. (18.23), and so on for
each of the four possible measurements. The outcomes of Alice’s measurements, and the
resulting state of Alice and Bob’s qubits, are summarized in Table 18.3. The two cbits
m, m
communicated to Bob make it possible to define the gates X
m
Z
m
on Bob’s wire
(Fig. 18.7), as also shown in Table 18.3. It is seen from the table that in the first case
(Alice measures |00) Bob’s qubit has collapsed into the state |q=α|0+β|1. Thus,
Alice’s original qubit |q has been successfully “teleported” to Bob. From the two cbits
m, m
= 0, 0, Bob is, thus, instructed to use the gates X
0
Z
0
= I , namely, to leave his
qubit unchanged. In the second case (Alice measures |01), Bob’s qubit is α|1+β|0,
and the application of X
0
Z
1
= Z swaps the amplitudes α, β to yield |q=α|0+β|1.
The last two cases are also straightforward to analyze.
The principle of QT can, thus, be summarized as follows: (a) Because Alice and
Bob share an ERP–Bell state, Alice’s measurements cause the system to collapse and
condition Bob’s qubit; (b) Alice communicating the two classical bits describing her
measurement makes it possible for Bob to retrieve Alice’s qubit |q. Remarkably, Alice
has no knowledge of the teleported |q. This point is quite important. Indeed, if Alice had
this knowledge, she could communicate to Bob the full information required (amplitudes,
base) for him to re-create the same qubit locally, and, therefore, they both would not need
this QT apparatus. However, such a communication is complicated and quite resource
consuming, should Bob need lots of qubits for his computations. And, most importantly,
Alice would be able to communicate only qubits known to her, which is utterly restrictive
in view of the QT potential. As a second observation, we note that QT does not violate the
noncloning theorem. Indeed, the initial qubit |qis collapsed by Alice’s first measurement
into the pure state |m, as seen from the top wire in Fig. 18.7.
The benefits of QT being now understood, we may then have a few legitimate ques-
tions. First, why use classical bits to determine which gates Bob should use? Indeed,
Alice’s measurements result in the collapse of her two qubits into the pure tensor state
370 Qubit measurements, coding, and teleportation
H
q
00
b
´
m
X
Z
m
´
m
q
m
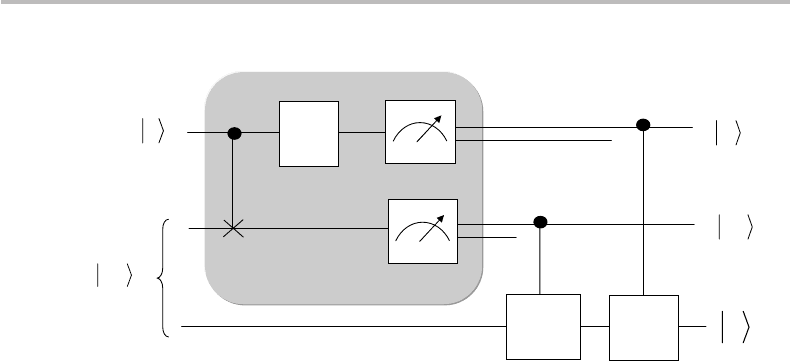
Figure 18.8 Principle of quantum teleportation with an all-quantum gate circuit.
|m|m
, and each of the |m, |m
qubits could be used as “automatic remote controls”
for Bob’s gates, i.e., controlled-X and controlled-Z. This would give the all-quantum-
gate QT circuit illustrated in Fig. 18.8. While such a circuit is logically equivalent to
that of the QT shown in Fig. 18.7, it has several drawbacks. First, controlled-U gates are
more complex than simple 2 × 2 U gates. But this is not as important as the fact that
if Alice and Bob were located far apart, the control qubits |m, |m
, even as known to
Alice, must be transported over this distance! It is, thus, far more sensible and straight-
forward for Alice to send the two bits m, m
to Bob through any classical channel, such
as the telephone or the Internet. On the other hand, if Bob is located nearby, or directly
on Alice’s premises, this whole qubit manipulation has no point, and the circuit shown
in Fig. 18.8 reduces to an elegant, but needless CROSSOVER circuit (a circuit that just
accurately transmits quantum information between Alice and Bob, who are in immediate
reach of each other!). Regardless of these different observations, the QT circuits shown
in the literature either use representations of Fig. 18.7 or of Fig. 18.8, or of both (the two
outputs of any of Alice’s measurement connecting to Bob’s gates).
Two other legitimate questions are whether it is possible to use EPR–Bell states
different from |β
00
, and how Alice and Bob can set up an EPR–Bell state to share.
Concerning the first question, the answer is yes, which is left as an exercise to show. In
that case, however, the classical bits to be transmitted to Bob are different from m, m
and
Alice must use a logic look-up table to transform m, m
into the right combinations, which
depends on which EPR–Bell state has been used. Apart from this minor complication, the
QT principle using the three EPR–Bell states |β
01
, |β
10
, |β
11
remains strictly identical.
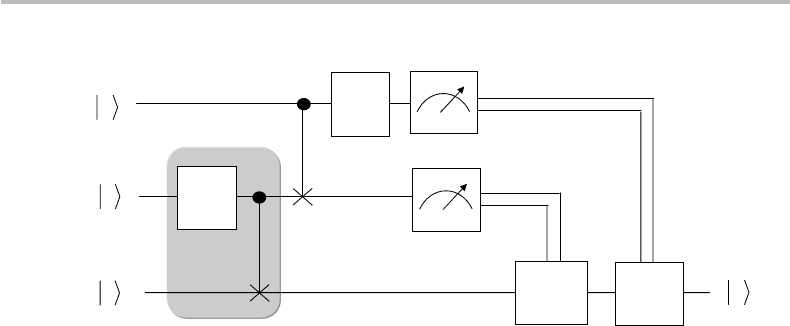
The answer to the second question is provided in Fig. 18.9. Both Alice and Bob must
supply a qubit |0of their own, for Alice to use as an ancilla qubit, and for Bob to use as
a target qubit. The Hadamard–CNOT circuit shaded in the figure corresponds to that of
Fig. 18.3, which, as we have seen, generates the entangled state |β
00
, when input with
the two qubits |0, |0.
As a summary and conclusion, we have learnt that it is possible to achieve the
teleportation of a single unknown qubit through a quantum channel. For the two ends of
the channel (Alice and Bob) the requirement is to share one EPR pair and two classical
18.5 Quantum teleportation 371
H
q
´
m
m
q
0
0
H
X
Z
Figure 18.9 Full implementation of quantum teleportation circuit with ancilla and target qubits
|0, |0 at input.
bits of information. The fact that Alice must communicate the two classical bits to Bob
shows that QT cannot operate faster than the speed of light, which is in agreement with
a fundamental principle of the theory of relativity. However, we have seen that Alice’s
measurements instantaneously collapse the system into any of the four 3-qubit states
givenbyEq.(18.23), namely,
|00(α|0+β|1);
|01(α|1+β|0);
|10(α|0−β|1);
|11(α|1−β|0);
(18.24)
which can be summarized in the general form: |mm
|ψ with |ψ=Z
m
X
m
|q being
the qubit accessible to Bob. It is clear that without any knowledge of the two bits
m, m
, Bob is not able to make any sense of his qubit |ψ, other than performing
meaningless random-measurement guesses. Bob cannot have any certainty either of
Alice’s measurement, through any prior agreement between them. No such agreement
is possible, since by definition any of Alice’s measurement of any of the four pure states
|mm
has
1
/
4
chance of being successful. Alice and Bob could agree that only the
measurement |00will be systematically performed, which already represents one bit of
advance information. Alice must then tell Bob if the measurement succeeded, and this is
another bit of information, resulting in m, m
= 0, 0. Only then can Bob be certain that
|ψ=|q. The key conclusion is that for successful qubit teleportation, Bob needs the
two classical bits m, m
from Alice. Should the QT apparatus use qubits instead of cbits
to control Bob’s gates, the conclusion remains the same: Alice’s qubits |m, |m
must be
transmitted over the distance separating her from Bob. Any physical channel supporting
qubits can be used for this transmission (for instance an optical fiber or a radio link), but
the communication cannot be faster than the speed of light.
1
1
In any physical medium, the speed of an electromagnetic (EM) wave is given by c = c
0
/n,wheren ≥ 1is
the medium’s refractive index and c
0
is the speed of light in absolute vacuum. Thus, the condition c ≤ c
0
is
always satisfied for any EM-wave transmission.

372 Qubit measurements, coding, and teleportation
q
´
q
B
X
B
1
2
3
4
c
y
5
6
X
Z
Z
´
B
X
Z
q
´
q
Bob
Alice
Alice
Bob
Figure 18.10 Circuit implementation for simultaneous quantum teleportation of two qubits.
What about the possibility of teleporting an arbitrary number N of different qubits
simultaneously or, even better, teleporting at once an N-qubit, also called quNit or,
equivalently, qudit,ford-qubit? The second case would achieve the “dream” of tele-
porting to another location any complex quantum system, like an atom, a molecule, a
crystal, or even a fragment of DNA, as may be already envisioned by some futurists. It
is beyond the scope of this chapter to address this issue and analyze, even superficially,
what type of protocol and resources would be required to achieve quNit teleportation,
in terms of shared entangled states and exchange of classical bits. We may, however,
venture one step further in the description by considering the teleportation of two qubits.
This description should suffice to illustrate the complexity of teleporting more than one
qubit, and also to satisfy a legitimate curiosity about the potentials of teleporting an
ensemble of quantum states.
A proposed circuit for the simultaneous teleportation of two qubits |q, |q
from
Alice is shown in Fig. 18.10, as an original, symmetrical variant of that shown in
Gottesman and Chuang (1999).
2
As seen from the figure, Alice and Bob share a 4-qubit
entangled resource, |χ , which I shall specify later. The two boxes labeled B, with two
cbit outputs each, correspond to Bell-state measurements. The rest of the circuit includes
three controlled-X and controlled-Z gates with Alice’s four cbits as control signals, to be
communicated to Bob via a classical channel. The circuit output, as received remotely
by Bob, is defined as |ψ=C
43
|q
3
|q
4
with |q
4
controlling |q
3
.Toretrieve|q, |q
,
Bob simply needs to pass the two qubits through the same CNOT gate, as shown at the
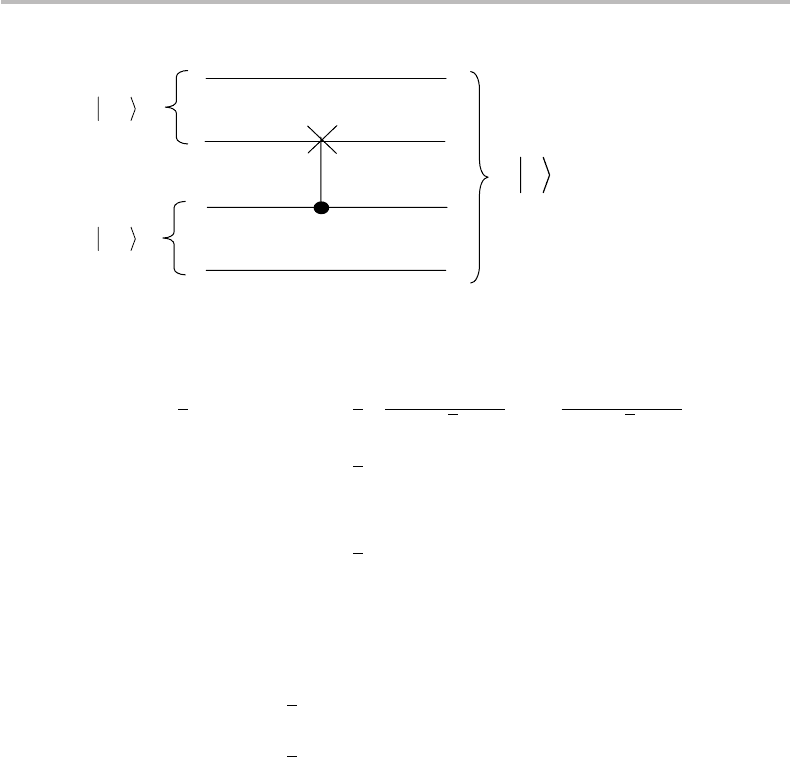
very right of Fig. 18.10. A possible circuit implementation to generate the entangled
state |χ is illustrated in Fig. 18.11. The circuit is seen to use two identical EPR–Bell
states |β
00
and one CNOT gate. Labeling the four quantum wires in Fig. 18.11 one to
2
From D. Gottesman and I. L. Chuang, Quantum teleportation is a universal computational primitive. Nature,
402 (1999), 390–3, http://arxiv.org/PS_cache/quant-ph/pdf/9908/9908010v1.pdf.
18.5 Quantum teleportation 373
b
00
b
00
c
Figure 18.11 Possible circuit implementation for generating the entangled state |χ in Fig. 18.10.
four, from top to bottom, we easily obtain the definition of |χ:
1
2
|β
00
12
⊗|β
00
34
=
1
2
|00
12
+|11
12
√
2
⊗
|00
34
+|11
34
√
2
=
1
4
(|00
12
⊗|00
34
+|00
12
⊗|11
34
+|11
12
⊗|00
34
+|11
12
⊗|11
34
)
≡
1
4
(|0000+|0011+|1100+|1111)
1234
.
(18.25)
Note the factor
1
/
2
, which was introduced to ensure proper normalization of the resulting
tensor state. The subsequent application of the CNOT gate C
32
with qubit 3 as control,
and qubit 2 as target finally yields:
|χ=
1
4
C
32
(|0000+|0011+|1100+|1111)
1234
≡
1
4
(|0000+|0111+|1100+|1011)
1234
.
(18.26)
It is seen from the above definition that |χ is a 4-qubit entangled state, which cannot be
expressed as any tensor product of the form |a
i
⊗|bcd
jkl
or |ab
ij
⊗|cd
kl
, with any
permutations of the indices i, j, k, l = 1, 2, 3, 4.
It is a rather involved and tedious task to check that the circuit in Fig. 18.10, together
with the communication to Bob of Alice’s measured cbits n, m, n
, m
, actually results
in the simultaneous teleportation of the two qubits |q
, |q. However, this represents
an excellent test case to apply all that we have learnt in this chapter, and the previous
ones as well, in terms of Pauli gates, tensor states, entangled states, measurements in the
Bell-state basis and quantum teleportation. For this specific reason, the full details of
the demonstration have been outlined in Appendix P. Going through this appendix, it is
observed that the 6-qubit pre-measurement state, |
, involves no less than 64 terms!
But the twin measurement executed thereupon from Alice results in the instant collapse
of |
into a single state of the form |nmn
m
1256
⊗|θ
34
. After hearing from Alice
what the four cbits n, m, n
, m
are, it is just a routine for Bob to set up his gate circuit
according to the sequence X
n
3
X
n
4
X
n
3
Z
m
4
Z
m
3
Z
m
4
, as indicated in Fig. 18.10. If the whole
exercise shows that teleporting a number of qubits greater than one is possible, it certainly

374 Qubit measurements, coding, and teleportation
illustrates that the corresponding quantum circuits become increasingly complex as this
number increases.
Superdense quantum teleportation is about maximizing the information contents
that can be communicated through a quantum channel, along with the necessary tax
of classical information of cbits. As evoked earlier, there exist many sophisticated
quantum circuits for the teleportation of single quNits of dimension n, as defined over
an orthonormal base V ={|i}
i=0...n−1
by
|q=γ
0
|0+γ
1
|1+γ
2
|2+···+γ
n−1
|n − 1, (18.27)
where γ
i
(i = 0 ...n − 1) are complex numbers. The first candidate immediately above
the qubit is the qutrit |q=γ
1
|1+γ
2
|2+γ
3
|3, which is a quantum superposition
of the classical trit or three-level information with values 0, 1, 2. Teleporting a single
qutrit requires Alice and Bob to share entangled 3-qutrit states, for instance the one
defined as |
+
=(|000+|111+|222)/
√
3, which is known as a three-level GHZ
(Greenberger–Horne–Zeilinger) state (the two-level being the first of the four Bell states,
|β
00
). The extra dimension opens up a large variety of approaches for teleportation
algorithms, in particular where a third party, called Charles, comes into the picture! The
mediation from Charles simplifies Alice’s task in terms of Bell-basis measurements, this
time in a 2-qutrit base. These considerations, which are beyond the scope of this book,
show at least that, mathematically speaking, teleportation in N dimensions knows no
actual limits.
18.6 Distributed quantum computing
The principle of quantum teleportation by means of EPR–Bell states can also be extended
to quantum gates. The basic concept is to act on remote qubits from a distance, which
is referred to as distributed quantum computation. One way to achieve this would
be for Alice and Bob to have their own independent quantum circuits, and use qubit
teleportation back and forth to perform computations on each other’s qubits. For this,
they would use a classical channel to exchange cbits, not only to teleport their qubit
data successfully, but also to instruct each other of the computations they want to see
the other party performing. For instance, if Alice wants to remotely execute a CNOT
operation onto Bob’s qubit, Bob needs first to send Alice his qubit, and Alice to send the
qubit resulting from her CNOT gate back to Bob. The single operation of this “remote”
CNOT computation, thus, consumes two EPR–Bell states (or ebits), and four classical
bits (or cbits).
Would it be possible to avoid such a complicated procedure, and instead conceive of
quantum gates being capable of acting directly on remote qubits? The answer is yes, and
the corresponding technique is called quantum gate teleportation. Within the scope of
this chapter, we may not venture into the complex details of quantum gate teleportation,
but I provide a generic example to show that it is possible, and also to show how this
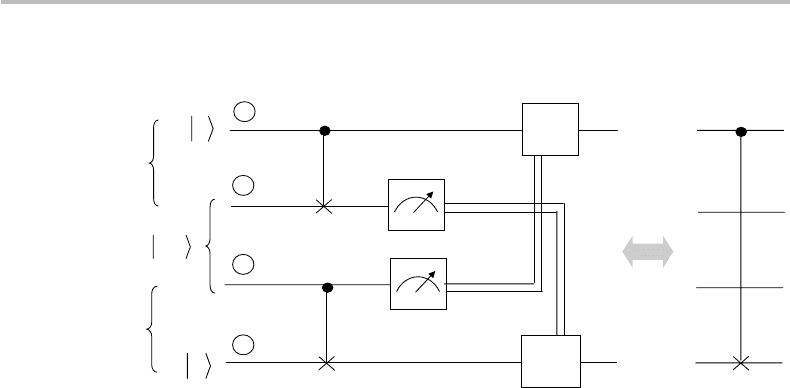
18.6 Distributed quantum computing 375
a
´
m
Z
m
x
1
2
3
4
12
C
34
C
X
Bob
Alice
14
C
(a) (b)
b
00
Figure 18.12 (a) 4-qubit circuit used for quantum teleportation of CNOT gate; (b) equivalent
distributed CNOT gate.
can work. Here, I shall describe the quantum teleportation of a CNOT gate,
3
which as
we have learnt from Chapter 16, is one of the universal building blocks for quantum
circuits. The principle of CNOT-gate teleportation is illustrated in Fig. 18.12. Locally,
Alice and Bob have the control of two qubits each, which are labelled 1 and 2 for Alice
(the first being called |a), and 3 and 4 for Bob (the last being called |x). As the figure
indicates, the qubits 2 and 3 are entangled through the EPR–Bell state |β
00
, thus, qubits
3 and 4 represent a shared ebit. Both Alice and Bob have local CNOT gates, called C
12
and C
34
, respectively. Furthermore,
r
Alice first measures qubit 3 in the base {|0, |1}, yielding a cbit m (namely, m = 0if
the qubit is |0 and m
= 1 if the qubit is |1);
r
Bob then measures qubit 3 in the different base {|+, |−}, yielding a cbit m
(namely,
m
= 0 if the qubit is |+ and m
= 1 if the qubit is |−).
Alice and Bob then use a classical channel to communicate to each other their respective
cbit measurement. To ensure the proper sequence order, Bob won’t proceed with his
own measurement until he has received cbit m from Alice. The cbit data m, m
are then
used locally by Alice and Bob to control their Z or X gates placed on the 1 or 4 qubit
paths, respectively, as indicated in Fig. 18.12.
Now I shall explain why the whole circuit shown in Fig. 18.12 is equivalent to
a distributed CNOT or C
14
gate, which uses Alice’s qubit 1, or |a, as the control,
and Bob’s qubit 4, or |x, as the target. Call |ψ
ij
the initial qubit pairs, labeled by
i, j. Hence, ψ
14
=|a⊗|x≡|ax (tensor state) and ψ
23
≡|β
00
(entangled state).
Call |0+
23
, |0−
23
, |1+
23
, |1−
23
,or|0+, |0−, |1+, |1−, for simplicity, the post-
measurement states generated by Alice and Bob’s measurements on the qubit pair 2 and
3. The demonstration of the circuit equivalence into a C
14
gate holds into the ad-hoc
3
See: Y.-F. Huang, X.-F. Ren, Y.-S. Zhang, L.-M. Duan, and G.-C. Guo, Experimental teleportation of a
quantum controlled-NOT gate. Phys. Rev. Letts., 93 (2004), id. 240501; see: http://arxiv.org/abs/quant-ph/
0408007.

376 Qubit measurements, coding, and teleportation
formula:
C
34
C
12
(|ψ
14
⊗|β
00
) =
|0+ ⊗ Z
0
X
0
C
14
|ψ
14
+|0− ⊗ Z
1
X
0
C
14
|ψ
14
+|1+ ⊗ Z
0
X
1
C
14
|ψ
14
−|1− ⊗ Z
1
X
1
C
14
|ψ
14
. (18.28)
The proof of this equation is left as a tedious, yet relatively easy exercise. From the
background of quantum teleportation we have gained in the previous section, and taking
the result for granted, the interpretation is, however, straightforward. Indeed, assume for
instance that Alice and Bob’s measurements result in the 2–3 state collapse into |0+,
yielding the cbits 0, 0. The result indicates that the 4-qubit output is |0+ ⊗ C
14
|ψ
14
and, in particular, that the qubit pair 1 and 4 is C
14
|ψ
14
≡CNOT|ax≡|a, a ⊕ x.
Alice does not know Bob’s target qubit |x, and Bob does not know Alice’s control
qubit |a, but both know for certain that the CNOT operation has been duly executed.
Likewise, in the case of a |0− collapse, it is found from the formal proof that the output
is X
4
C
14
|ψ
14
, with X
4
being carried upon the qubit 4, hence the need to apply X again
on this qubit (recalling that X
2
= I ), to transform the result into C
14
|ψ
14
.Thesame
reasoning applies to the other two collapse cases |1+ and |1−.
In summary, the above description exemplifies that it is possible to achieve the quan-
tum teleportation of a CNOT gate, with the only resource of one shared ebit and two
cbits. Various teleportation schemes exist for other gate types, for instance controlled-Z
(also called CSIGN for “controlled sign”), which involve somewhat more gate-intensive
quantum circuits and ebit resources.
4
18.7 Exercises
18.1 (B): Show that there exists no tensor product of single qubits able to generate any
of the Bell–EPR states:
|β
00
≡
1
√
2
(|00+|11),
|β
01
≡
1
√
2
(|01+|10),
|β
10
≡
1
√
2
(|00−|11),
|β
11
≡
1
√
2
(|01−|10).
18.2 (M): Show that quantum teleportation is possible with EPR–Bell states
|β
01
, |β
10
, |β
11
.
4
See, for instance: www.iqc.ca/activities/projects/msilva01.php.
