Desurvire E. Classical and Quantum Information Theory: An Introduction for the Telecom Scientist
Подождите немного. Документ загружается.


18.1 Measuring single qubits 357
measurements indexed by m (m = 1...n). To recall, the two requirements for any such
set are (a) that all operator products M
+
m
M
m
should be positive (which result in the
unitarity of M
+
m
M
m
), and (b) that they satisfy the completeness relation
M
+
m
M
m
= I .
The two key results are, first, that the probability of measuring m is given by the bracket:
p(m) =ψ|M
+
m
M
m
|ψ, (18.1)
and, second that the measurement projects the input state |ψinto the post-measurement
state |ψ
defined as
|ψ
=
1
p(m)
M
m
|ψ=
1
ψ|M
+
m
M
m
|ψ
M
m
|ψ. (18.2)
Out of many possibilities for any quantum measurement, we can use the measurement in
the state basis, where M
m
=|x
m
x
m
| is the projector on the pure state |x
m
.Giventhe
state |ψ=
x
i
|x
i
, it is clear from the definition in Eq. (18.1) with M
+
m
M
m
=|x
m
x
m
|
that the probability that the measurement finds |ψ in the state |x
m
is p(m) =|x
m
|
2
.As
we have seen in Chapter 17, the post-measurement state is
|ψ
=
x
m
|x
m
|
|x
m
. (18.3)
Let the input state be a qubit |q=α|0+β|1, as defined from the orthonormal base
V ={|0, |1}, and where (to recall) α, β are complex numbers satisfying |α|
2
+|β|
2
=
1. It is clear that α, β represent the complex probability amplitudes of the qubit state, and
that |α|
2
or |β|
2
represent the probabilities of the qubit being found in either pure state
|0 or |1 of the base V . According to Eq. (18.3), the corresponding post-measurement
states are
α
|α|
|0=e
iδ
α
|0
β
|β|
|1=e
iδ
β
|1,
(18.4)
where
e
i
δ
α
,
e
i
δ
β
are unobservable phase factors, which can be omitted.
Since the qubit is a superposition of states |q=α|0+β|1, the action of any
measurement in the state-base V , as defined by the operators M
0
=|00|or M
1
=|11|,
is, thus, to project, or collapse it into one of the two states |0 or |1.UsingM
0
,the
probability that |q collapses into |0 is p(0) =|α|
2
.UsingM
1
, the probability that
|q collapses into |1 is p(1) =|β|
2
= 1 −|α|
2
. We can interpret the result of such
a measurement as reducing the qubit information into the classical bit values 0 or
1, respectively. But unlike the classical case, there is no absolute certainty that the
resulting information is, indeed, 0 or 1, when using measurement operators M
0
, M
1
, since
either outcome is associated with some finite probabilities. For illustration, consider the
following possibilities:
(a) α = 0,β = 1, yielding p(0) = 0, p(1) = 1;
(b) α = β = 1/
√
2, yielding p(0) = p(1) = 1/2;
(c) α = 1/
√
3,β= 2/
√
3, yielding p(0) =1/3, p(1) = 2/3;
(d) α = 0.9,β= 0.1, yielding p(0) =0.99, p(1) = 0.01.

358 Qubit measurements, coding, and teleportation
It is clear that in case (a), there is absolute certainty that the qubit measurement will
result in the bit information 1. In case (b), the outcome has equal chances of being
0 or 1. In case (c) the odds on measuring 1 are twice those of measuring 0. In case
(d), the odds are 99% for 0 and 1% for 1. It must be emphasized here that the above
figures concern the measurement outcomes obtained by using the corresponding opera-
tors M
0
, M
1
. Here comes a subtlety: in case (c), for instance, we know that we have a
1/3 chance of measuring 0 when using M
0
. This means that there is a 2/3 chance that
this measurement fails. Likewise, there is a 1/3 chance that the measurement of 1 fails
when using M
1
. But what does “measurement failure” mean? Basically, that whenever
we choose to use a given measurement projector M
m
, the input state is not absolutely
certain of collapsing into the corresponding state |x
m
. It will only happen “successfully”
with probability |x
m
|
2
. If this collapse does not happen (with probability 1 −|x
m
|
2
), then
nothing is measured, and the measurement is, thus, failed. Also, the quantum state col-
lapses into nothingness, which here means qubit annihilation and irreversible loss of its
information. We can mathematically define such an annihilated, informationless state as
|q
=∅.
To clarify the picture, or to alleviate some possible unease with the notions of “suc-
cessful” and “failed” qubit measurements, consider the following (fictitious) physical
analogy, which we have already used in Chapter 17 for POVM measurements.
Compare the qubit |q with a source that has two possible tones, A or B (standing for
the states |0 or |1, respectively), and which are not visible to the eye. Our measurement
consists of determining the color tones by observing this source through a set of two
“magic filters,” called 0, 1(forM
0
, M
1
). As we have seen earlier, such filters have
strange properties. Indeed, filter 0 does not react to tone B, while it makes tone A
visible to the eye, but only with probability p (or |α|
2
). Filter 1 does not react to tone
A, while it makes tone B visible to the eye, but only with probability q = 1 − p (or
|β|
2
). Even stranger here (than the description in Chapter 17) is that the two filters
A, B are of complementary nature, since their probabilities of positive reaction are now
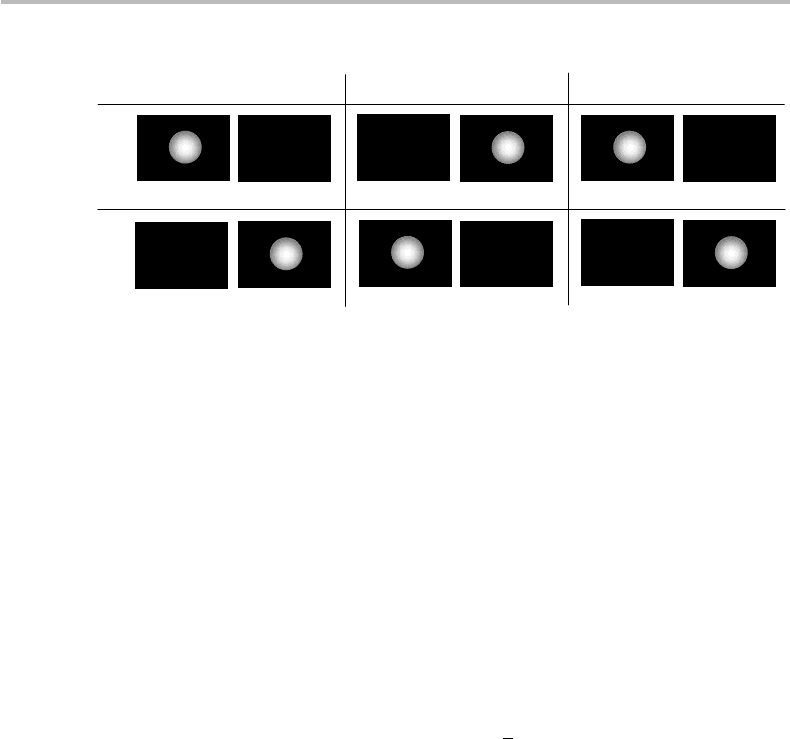
complementary (q = 1 − p). Figure 18.1 shows the eye images obtained in the eight
possible cases, according to the two pure-tone possibilities A or B (but not both) and
their mixture A, B, and the two filter options 0, 1. The observation of a bright spot
indicates a positive, or successful, measurement (seeing something). The absence of a
spot indicates a negative, or failed, measurement (not seeing anything).
Considering first the case of pure tones (A or B), the figure indicates that there are
actually two “successful” measurement outcomes, as characterized by the presence of
the bright spot with nonzero probability. These successes correspond to the two input or
filter cases ( A, 0), (B, 1), which positively identify the tones to be A or B with absolute
certainty ( p = 1forA,orq = 1 − p = 1forB). In the two other cases, ( A, 1), (B, 0),
we never see any spot, or the measurement is always “failed.” But here comes a subtlety:
if we know prior to the measurement that the color tones are pure, the failed measurement
is also a positive indication. Indeed, a failure to measure A means an absolute certainty
that the input is B, and the reverse. The certainty is the same regardless of our filter choice
(0 or 1). In this case, the classical bit measurement from the qubit is 100% accurate. The
18.1 Measuring single qubits 359
A
0
1
1
B
x
0
p
0
1
1 −
p
1 −
p
1
0 1
0
A
,
B
p
Figure 18.1 Fictitious analogy of qubit measurement of tones A, B, or their mixture, and a
magic-filter set 0, 1 to characterize a source. Given the tones A, B and choices 1, 2, a positive
observation of the tone is characterized by the bright spot on the images shown, with various
probabilities 1, 0, p, 1 − p.
information gained is a 0 or 1 classical bit, in 100% correspondence with the qubit pure
state. But to achieve this performance without any concern for the measurement option
(M
0
, M
1
), it costs the tax of one bit of advance information (i.e., “pure input state?” =
YES, NO). In the case of the tone mixture (Fig. 18.1, right) we observe only two
measurement “successes,” with probability p when using the filter 0, and probability
1 − p when using the filter 1. The information obtained in these two cases is a classical
bit of information 0 or 1, as we have projected the qubit onto the corresponding pure
states. But, as the figure indicates, there is a finite probability 1 − p or p that using
either filter 0 or 1 results in a measurement failure, and in these cases we do not get any
classical bit information. There is one exception to this, however: if we know in advance
that the qubit is in the superposition α = β = 1/
√
2 (case (b)), there are equal chances
of success or failure, regardless of the measurement operator (or tone filter). There is no
point in making any measurement, since we know for a fact that a successful outcome
will give either a 0 or a 1 classical bit, with equal likelihood. We may just pick a bit
value at random. The tax to pay for this result is one bit of advance information (i.e.,
“case (b)?” = YES, NO).
The above description, despite its questionable usefulness from a purist or academic
standpoint, made it possible to “visualize” somewhat and get a better feel of the nature of
quantum measurements, when applied to single qubits. It is noteworthy, however, that the
fictitious “magic-filter” experiment can actually be implemented in the physical world,
as described in Chapter 25 in the part concerning quantum cryptography. The lesson
learnt is that any “successful” qubit base-state measurement results in its collapse into
one of the pure states, and the reduction of its intrinsic information into a classical 0 or
1 bit.
In Chapter 17, we have also described another type of measurement referred to as
projective or von Neumann measurement. In this approach, we can define the Hermitian
observable A according to its spectral decomposition over the eigenstates |λ
0
, |λ
1

360 Qubit measurements, coding, and teleportation
forming an orthonormal base V ={|λ
0
, |λ
1
}:
A =
2
m=1
λ
m
P
m
=
2
m=1
λ
m
|λ
m
λ
m
|
≡ λ
0
|λ
0
λ
0
|+λ
1
|λ
1
λ
1
|,
(18.5)
where λ
0
,λ
1
are the corresponding eigenvalues, and P
m
=|mm| the measurement
operators. Next, we recall the two key results obtained in Chapter 17, while applying
them to the case of qubits. First, given a qubit |q=x
0
|λ
0
+x
1
|λ
1
as expressed
in the eigenstate base V , the probability of measuring the eigenvalue λ
m
is given
by p(λ
m
) =|x
m
|
2
. With the usual qubit notations |q=α|λ
0
+β|λ
1
, we, thus,
obtain:
p(λ
0
) =|α|
2
, p(λ
1
) =|β|
2
. (18.6)
Second, the post-measurement state |q
is
|q
=|λ
m
. (18.7)
We may conclude from the two above results that the projective measurement of qubits is
essentially similar to the previously described base measurement in the pure states, except
that the measurements project the qubit onto the eigenstates of A. Such a conclusion
is true, but it fails to convey an important property. Indeed, if we know prior to the
measurement that the qubit must be in one of the eigenstates, then we are in the same
situation as in the previous pure-state case. No matter whether we use P
0
=|λ
0
λ
0
| or
P
1
=|λ
1
λ
1
| for the qubit measurement, we always retrieve a classical 0 or 1 bit. To
recall, if we use P
0
when the qubit is in state |λ
0
or P
1
when the qubit is in state |λ
1
,
the measurements are certain to “succeed,” yielding the classical 0 or 1 bits, and the
collapsed qubit state remains invariant. But if we use the wrong operator (e.g., P
0
when
the qubit is |λ
1
), the measurement “fails,” and the qubit state is annihilated. However,
such a failure indicates that the qubit must have been in the other orthogonal state, and,
therefore, we can conclude with certainty the value of the corresponding classical bit.
The only penalty in this event is that we have lost the qubit, and it cannot be reused for
another quantum computation, for instance as an input to a subsequent quantum gate
within a quantum circuit. The key conclusion is that measurements can be destructive
(even when informative) and, therefore, it is safer to proceed to quantum measurements
only at the end of a purposeful computational chain. If intermediate measurements are
required, one must ensure that these are always nondestructive, so that the collapsed
qubit may be reused in the rest of the circuit computation.
In quantum-gate circuits (Chapter 16), any quantum measurement is conventionally
represented by an “ammeter” symbol, as illustrated in Fig. 18.2. The two output lines
shown at the right correspond to the collapsed or post-measurement state (|λ
m
) and
to the measurement value λ
m
. In the case where the measurement fails, we may write
|q
=∅for the input state annihilation.

18.2 Measuring
n
-qubits 361
q
m
q
=´
m
m
M
l
l
Figure 18.2 Quantum-circuit representation of measurement apparatus to measure qubits with
operator M
m
, yielding measurement value λ
m
.
18.2 Measuring
n
-qubits
In this section, I describe quantum measurements of higher-order or n-qubits, which
have fundamental implications in both QIT and quantum computing (QC). This is a
turning point, where we shall begin to grasp the strange beauty (and the oddity!) of the
quantum properties of qubits.
As we have seen in Chapter 17, any base-state measurement E
im
on an n-state |ψ
from V
⊗n
results in the collapsing effect
E
im
|ψ=E
im
|ψ
1
,...,ψ
n
=|ψ
1
,...,ψ
i−1
, m,ψ
i
,...,ψ
n
.
(18.8)
In the case of an n-qubit |q=|x
1
, x
2
,...,x
n
, with x
i
= 0, 1, we have:
E
im
|q=E
im
|x
1
, x
2
,...,x
n
=|x
1
, x
2
,...,x
i−1
, m, x
i+1
,...,x
n
.
(18.9)
With this measurement tool in hand, we can now perform measurements on any qubit
superpositions or mixtures in the subspace V
⊗2
(for instance), such as:
|q=u|x
1
, x
2
+v|x
1
, x
2
, (18.10)
with u,vbeing complex amplitudes satisfying |u|
2
+|v|
2
= 1, so that |rhas a modulus
of one. For each qubit i in the subspace V , there are two possible measurement operators,
namely E
i1
and E
i2
. To illustrate the action of these operators, consider the following
example (using the compact notation |x
i
, x
j
≡|x
i
x
j
):
|q=
1
√
3
(|00+|01+|10). (18.11)
If we want to measure a classical bit 0 in the first qubit position (i = 1), we use E
10
and
obtain
E
10
|q=
1
√
3
(E
10
|00+E
10
|01+E
10
|10)
=
1
√
3
(|00+|01+∅)
=
1
√
3
(|00+|01).
(18.12)

362 Qubit measurements, coding, and teleportation
Thus, the probability of measuring 0 in the first qubit is:
p
i=1
(0) =q|E
10
|q=
1
3
(00|+01|)(|00+|01) ≡
2
3
. (18.13)
It is now a straightforward exercise to evaluate mentally the other probabilities:
p
i=1
(1) =
1
3
, p
i=2
(0) =
2
3
, p
i=2
(1) =
1
3
. (18.14)
Next, we shall look at a peculiar family of some 2-qubits, which are of utmost interest for
qubit measurements and for the “quantum manipulation” of information. In Chapter 15,
we identified four state superpositions, referred to as Einstein–Podolsky–Rosen (EPR)
or Bell states (or pairs), and defined:
|β
00
≡
1
√
2
(|00+|11)
|β
01
≡
1
√
2
(|01+|10)
|β
10
≡
1
√
2
(|00−|11)
|β
11
≡
1
√
2
(|01−|10).
(18.15)
These EPR–Bell states may seem innocuous at first glance, but they actually reserve
a certain number of interesting properties, and as we shall see further down, really
“stunning” applications.
As a first property, there exists no tensor product of pure states or of qubits that is
capable of generating any of the EPR–Bell states. This is left as a straightforward exercise
to check. Because the EPR–Bell states cannot be decomposed as a qubit tensor product,
they are called entangled states. A faster way to realize the nature of entanglement is to
observe that none of the states in Eq. (18.15) can be factorized into a pure-state product
of the form |i|j =|0|0, |0|1, |1|0, |1|1. Thus, it is not possible to tell what the
states of the first and the second qubits are.
While the EPR–Bell states are not tensor products of qubit states, they can, however, be
generated by means of quantum gates. The circuit shown in Fig. 18.3, which comprises
a Hadamard gate and a CNOT gate (Chapter 16) represents one possibility for the
generation of EPR–Bell states. As we saw in that earlier chapter, the Hadamard gate
transforms the input qubit |0 into the mixed state |+ = (|0+|1)/
√
2, and the input
qubit |1 into the mixed state |− = (|0−|1)/
√
2. Thus, for the quantum gate in
Fig. 18.3, the tensor input |0⊗|y results in
(H |x) ⊗|x ⊕ y=(|x = 0+|x = 1) ⊗|x ⊕ y/
√
2
= (|0⊗|0 ⊕ y+|1⊗|1 ⊕ y)/
√
2
≡ (|0, y+|1, 1 ⊕ y)/
√
2.
(18.16)
Hence, |0⊗|0→(|0, 0+|1, 1)/
√
2 ≡|β
00
and |0⊗|1→(|0, 1+|1, 0)/
√
2 ≡|β
01
. The two other results for the inputs |1⊗|y are also readily verified.

18.2 Measuring
n
-qubits 363
H
x
xy
y
b
Figure 18.3 Quantum circuit for the generation of EPR–Bell states |β
xy
as defined in Eq. (18.15).
As a second property, the EPR–Bell states form an orthonormal basis for any 2-qubit
|kl and any superposition thereof. Indeed, it is straightforward to see from Eq. (18.15)
that
|00=
1
√
2
(|β
00
+|β
10
)
|01=
1
√
2
(|β
01
+|β
11
)
|10=
1
√
2
(|β
01
−|β
11
)
|11=
1
√
2
(|β
00
−|β
10
),
(18.17)
hence, any 2-qubit superposition of the above pure |ij states accepts a unique decom-
position over the EPR–Bell states.
Third, we notice from the definitions in Eq. (18.5) that the EPR–Bell states represent a
mix of 2-qubits |ijand |klsatisfying i = 0, k = 1, and j, l = 0, 1. For the measurement
probabilities, this leads to the following property (as is easily mentally checked):
p
i=1
(0) = p
i=1
(1) = p
i=2
(0) = p
i=2
(1) =
1
2
. (18.18)
This result shows that any measurement E
im
of the EPR–Bell states has a 50% chance
of successfully projecting into any of the pure states. The 16 possible measurements
resulting in the corresponding state collapses (phase factors
e
−
i
π/2
being omitted) are
summarized in Table 18.1. As expected, we observe from the table that the EPR–Bell
states collapse into any of the pure states |00, |01, |10, |11. We see that using a
positive measurement E
1m
necessarily collapses the EPR–Bell pair into the pure state
|m⊗|x, and a positive measurement E
2m
necessarily collapses the EPR–Bell pair into
the pure state |x⊗|m, where x = 0, 1. This has the consequence that regardless of the
four possible EPR–Bell pairs, a single positive measurement yields absolute information
on one of the two qubits in the collapsed state.
Because the first measurement gives only one qubit information, a second measure-
ment would be necessary to get the missing information concerning the other qubit. But
we do not need to make a second measurement if we know in advance the initial EPR–Bell
pair. Indeed, Table 18.1 illustrates that the advance knowledge of |β
00
, |β
01
, |β
10
, |β
11
364 Qubit measurements, coding, and teleportation
Table 18.1 State collapses resulting from single-qubit measurements E
im
on the EPR–Bell states |β
00
, |β
01
, |β
10
, |β
11
.
|β
00
|β
01
|β
10
|β
11
E
10
|00|01|00|01
E
11
|11|10|11|10
E
20
|00|10|00|10
E
21
|11|01|11|01
()
1001
2
1
01
+=
b
Alice
Bob
10
Measures
20
E
Collapse
11
E
Measures
Figure 18.4 Two successive measurements by Alice then Bob in an entangled quantum state, here
|β
01
.
and the choice of a single-measurement operator E
10
, E
11
, E
20
, E
21
absolutely defines
the collapsed state and, hence, the value of the two entangled qubits. For instance, if
we use |β
11
, the single measurement E
21
yields the 2-qubit |01=|0⊗|1 and the
absolute information therein. Thus, given the knowledge of the system EPR–Bell pair,
any positive measurement of one of the two qubits conditions the information knowledge
of the other qubit. Because the information of one qubit measurement conditions that
of the second qubit measurement, the EPR–Bell states are said to be entangled.InQIT
jargon, EPR–Bell states are also referred to as ebits, for “entanglement bits” (one ebit =
one single entangled pair).
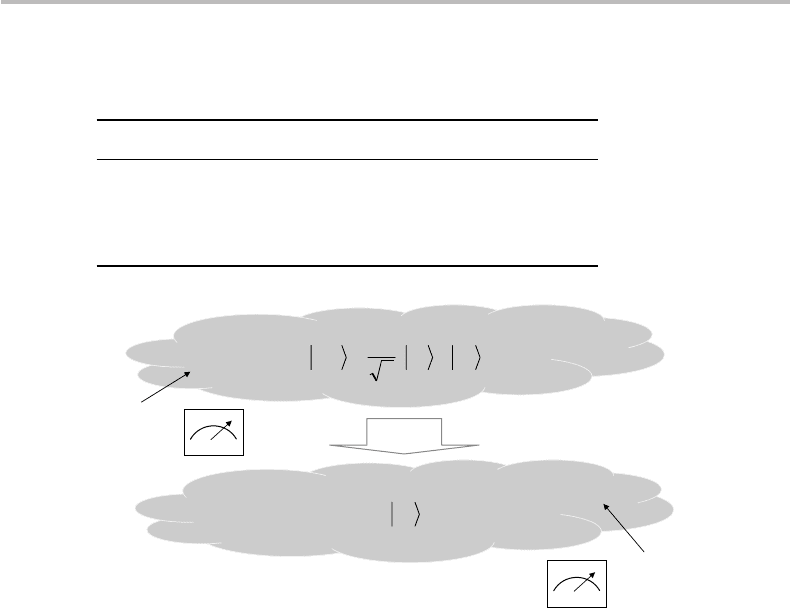
To provide a visual illustration of this, imagine two people A and B, who are tradi-
tionally named Alice and Bob, and who live far apart. However, both have access to a
quantum system, which is in the entangled EPR–Bell state |β
01
, as represented by a
cloud in Fig. 18.4. The state remains in |β
01
until Alice unilaterally takes the initiative
to measure the first qubit, through the operator E
11
, for instance. This measurement
immediately results in the EPR–Bell pair collapsing into the pure state |10. Bob’s mea-
surement of the second qubit can only yield |0 as a positive outcome. Bob and Alice
can exchange roles. For instance, Bob may first measure the second qubit through E
20
,
resulting in the system collapsing into the state |01, and leaving |0 to Alice as the only
positive measurement for the first qubit. In each case, the measurement of the first qubit
conditions the measurement of the second, because of the effect of state collapse that
occurs in between.
18.3 Bell state measurement 365
Table 18.2 Outcome of Bell measurement with EPR–Bell states as input (normalization
factor being overlooked).
Input state |xy Pre-measurement state Cbit output m, m
|β
00
=|00+|11|00 00
|β
01
=|00+|11|01 01
|β
10
=|00−|11|10 10
|β
11
=|01−|10|11 11
H
x
y
´
m
m
Figure 18.5 Principle of Bell measurement or measurement in Bell states.
From any physical perception of our “classical world,” the effect of state entanglement
seems rather nonintuitive. We may illustrate it through a figurative experiment. Assume
that we place two coins in two separate boxes. In each box, the position (or states) of
the coins can be either heads or tails, but we have no awareness of which one. In the
classical world, opening a box tells us only that the coin is heads or tails, but we cannot
know of the other coin until we open the other box. In the quantum world, the coin states
may be entangled. This means that opening only one box conditions the state of the coin
in the other box. The point here is not about the advance knowledge of the entanglement
possibilities, as represented by the four possible EPR–Bell states. Rather, it is the matter
that a single measurement in one physical system determines “for absolute certain”
the state of the other physical system. As described later in this chapter, the properties
of EPR–Bell state entanglement are the key to applications called quantum superdense
coding and quantum teleportation, both of which having no counterpart in the classical
world.
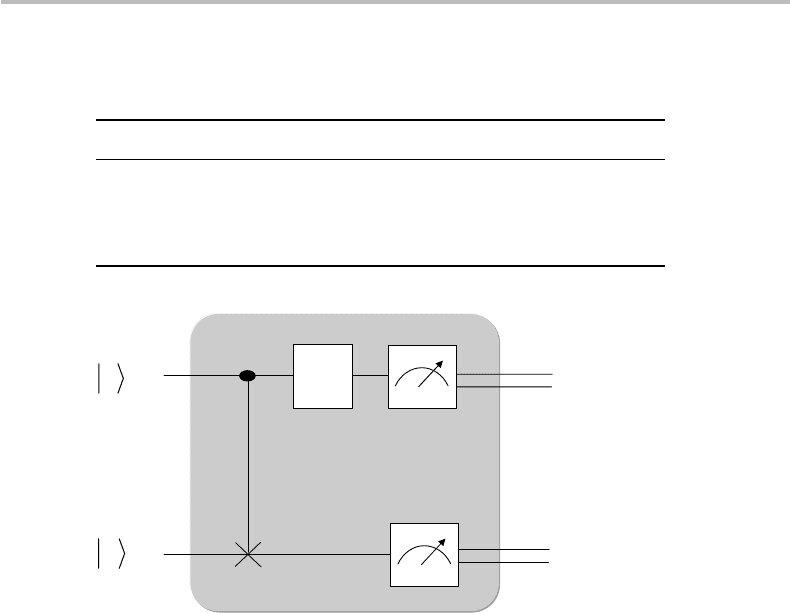
18.3 Bell state measurement
In this section, I describe a 2-qubit measurement scheme, referred to as measurement in
the Bell basis,orBell state measurement. The principle is illustrated in Fig. 18.5.The
circuit includes a Hadamard gate and a CNOT gate, followed by two qubit measurements.

366 Qubit measurements, coding, and teleportation
U
00
b
Bob
Alice
H
m
´
m
Figure 18.6 Circuit used for superdense coding.
The measurements, which are made in the base {|00, |01, |10, |11}, output the clas-
sical bits m, m
. What happens if we input to this gate circuit any of the EPR–Bell states
|β
mm
? It is left as a simple exercise to check that the pre-measurement states are |mm
and the resulting measurement cbits (short for “classical bits”) are m, m
,asshownin
Table 18.2. This means that the apparatus is able to positively single out or identify any of
the four EPR–Bell states, hence, the name “measurement in the Bell basis” or “Bell state
measurement.” Such a denomination may sound confusing, since the measurement is
actually performed in the {|00, |01, |10, |11}basis. The point is that while the circuit
represents a true EPR–Bell state measurement apparatus, it can be used for other types
of application, as will be shown next when describing superdense coding and quantum
teleportation.
18.4 Superdense coding
In this section, I describe a first application of quantum entanglement, which enables
quantum superdense coding. The key concept behind this appellation is the possibility
for Alice to send to Bob two classical bits m, m
, which she has in her possession, by
means of communicating only a single qubit. The generic circuit for superdense coding
is represented in Fig. 18.6. Alice and Bob must share an EPR–Bell state, for instance
|β
00
. Alice controls a gate U , which she can change at will into I, Z, X , and iY.Bob
has the control of a Bell-state measurement apparatus, as shown by the shaded subsystem
in the figure. It can be checked as an easy exercise that the choice of U transforms |β
00
into any EPR–Bell state |β
00
, |β
10
, |β
01
, |β
11
, according to
I |β
00
=|β
00
; X |β
00
=|β
01
Z|β
00
=|β
10
; iY|β
00
=|β
11
.
(18.19)
Thus, by switching the U gate into I , Z , X, and iY, Alice can send Bob the classical
bit pairs 00, 01, 10, and 11, respectively, at an information rate of two bits per qubit,
which represents twice the classical information rate, hence the name superdense coding.
Note that from any realistic telecom viewpoint, twofold improvements in information-
rate capacities do not deserve such superlatives as “super” or “dense,” or, worst of
all, “superdense,” notwithstanding the conceptual importance of the potential capacity
expansion of the “old-fashioned” classical bit.
