Desurvire E. Classical and Quantum Information Theory: An Introduction for the Telecom Scientist
Подождите немного. Документ загружается.


16.5 Tensor products 327
tum algorithms simply emulate classical ones, with qubits instead of bits! (Chapter 19
and 20 will prove far differently).
16.5 Tensor products
In previous sections, we made use of the notion of tensor product for qubits, to describe
quantum gates with more than one qubit input. This section will make it possible to
clarify such a notion, which is fundamental to the understanding of quantum computing
with multiple states. In the description, we shall proceed gradually, from elementary to
advanced.
Given two qubits |a, |b we called the tensor product the 2-qubit |a|b.Fromnow
on, we shall write the result with the new notation |a|b≡|a⊗|b, with the sign ⊗
standing for the tensor-product operation. Given the computational base V ={|0, |1},
which defined a 2D qubit space, we can form the 4D extended base defining a 4D 2-qubit
space V ⊗ V according to:
V ⊗ V ={|0, |1} ⊗ {|0, |1}
={|0|0, |0|1, |1|0, |1|1}
≡{|0⊗|0, |0⊗|1, |1⊗|0, |1⊗|1}.
(16.45)
In the extended base, |a⊗|b is represented by four complex coordinates
(u
1
, u
2
, u
3
, u
4
) to be determined. Assuming that |a=a
0
|0+a
1
|1 and |b=b
0
|0+
b
1
|1, we obtain
|a⊗|b=(a
0
|0+a
1
|1) ⊗ (b
0
|0+b
1
|1)
= a
0
b
0
|0⊗|0+a
0
b
1
|0⊗|1+a
1
b
0
|1⊗|0+a
1
b
1
|1⊗|1,
(16.46)
hence (u
1
, u
2
, u
3
, u
4
) ≡ (a
0
b
0
, a
0
b
1
, a
1
b
0
, a
1
b
1
). In the above, we have implicitly made
use of the linearity and distribution-over-addition properties of the tensor product:
λ(|x⊗|y) = λ|x⊗|y=|x⊗λ|y
|x⊗(|y+|z) =|x⊗|y+|x⊗|z.
(16.47)
The notion of tensor product, along with the same properties, applies to any two nD
and mD spaces defined by computational basis V ={|α
1
, |α
2
,...,|α
n
} and W =
{|β
1
, |β
2
,...,|β
m
}. Hence, given
|a=
n
i=1
a
i
|α
i
, |b=
m
j=1
b
j
|β
j
, (16.48)
we have
|a⊗|b=
n
i=1
m
j=1
a
i
b
i
|α
i
⊗|β
i
. (16.49)
A qubit |a that is tensored with itself n times will be noted |a
⊗n
, namely,
|a
⊗n
=|a⊗|a⊗,...,⊗|a
n times
. (16.50)

328 Quantum bits and quantum gates
The tensor state |a⊗|b, often noted |a, b for simplification, is also referred to as a
joint state. Such a joint state corresponds to the description of two quantum systems,
themselves being in the states |a and |b, respectively. Thus, |a⊗|a corresponds to
the description of two systems being in the same state |a. However, such a possibility
should not lead one to the conclusion that given a quantum system in state |a,itis
possible to duplicate this state into a second quantum system, so as to obtain the joint
state |a⊗|a. It simply cannot be achieved. This is a result of the noncloning theorem,
which is described in Section 16.6.
Next, I shall introduce the notion of tensor product for linear operators (which so
far have been referred to as matrices operating on the qubit vector space). Assume an
operator A defined on the |a qubit space and an operator B defined on the |b qubit
space. The operator tensor product A ⊗ B applies to the tensor states |a⊗|b and is
defined according to the following distribution rule:
A ⊗ B(|a⊗|b) = A|a⊗B|b. (16.51)
An operator A that is tensored with itself n times will be noted A
⊗n
, namely,
A
⊗n
= A ⊗ A⊗,...,⊗A
n times
. (16.52)
The operator tensor product A ⊗ B also satisfies the useful properties according to which
conjugation, transposition, and Hermitian conjugation
12
are distributive. Namely:
(A ⊗ B)
∗
= A
∗
⊗ B
∗
(A ⊗ B)
T
= A
T
⊗ B
T
(A ⊗ B)
+
= A
+
⊗ B
+
.
(16.53)
These three properties stem from the definition of the operator tensor product in
Eq. (16.51), in which the operations of transposition and complex or Hermitian conju-
gation are clearly distributive.
How can we derive the matrix of the tensor operator A ⊗ B? The rule, which is
referred to as the Kronecker product, is quite simple. Assume that A is represented by a
n × m matrix (n lines, m columns), with coefficients A
ij
(i = 1,...,n, j = 1,...,m).
We have, by definition
A ⊗ B =
A
11
BA
12
B ··· A
1m
B
A
21
BA
22
B ··· A
2m
B
.
.
.
.
.
. ···
A
n1
BA
n2
B ··· A
nm
B
. (16.54)
Thus, in the above reduced form, A ⊗ B is an n × m matrix with coefficients A
ij
B.IfB
is represented by a p × q matrix ( p lines, q columns), then A ⊗ B is clearly an np × mq
matrix. The Kronecker-product rule also applies to single-column matrices, or vectors,
12
To recall, for any operator A of matrix coefficients A
ij
, the conjugate operator A
∗
has for coefficients
A
∗
ij
(complex conjugate of A
ij
), the transposed operator A
T
has for coefficients A
ji
, and the Hermitian-
conjugate (or adjoint) operator A
+
has for coefficients A
∗
ji
. Also, the transposed and Hermitian conjugate
of the product AB are (AB)
T
= B
T
A
T
and (AB)
+
= B
+
A
+
, respectively.

16.5 Tensor products 329
which enables one to calculate the tensor product |a⊗|b. Let us next examine some
illustrative examples.
First, consider the case of the qubit tensor product |a⊗|bin bases V ={|α
1
, |α
2
}
and W ={|β
1
, |β
2
, |β
3
}. The corresponding matrices are single column, with A
i1
=
a
i
and B
i1
= b
i
. We obtain:
|a⊗|b=
a
1
|b
a
2
|b
=
a
1
b
1
b
2
b
3
a
2
b
1
b
2
b
3
=
a
1
b
1
a
1
b
2
a
1
b
3
a
2
b
1
a
2
b
2
a
2
b
3
, (16.55)
which is the expected result.
Second, consider the tensor product X ⊗ Y of the two Pauli matrices X, Y . We obtain:
X ⊗ Y =
0 × Y 1 ×Y
1 × Y 0 ×Y
=
0 Y
Y 0
=
000−i
00i0
0 −i0 0
i000
.
(16.56)
It is left as an easy exercise to verify the property X ⊗ Y (|a⊗|b) = X|a⊗Y |b,
which, as we have seen, applies to any pairs of operators A, B and qubits |a, |b.
An interesting case of n-tensored operator is provided by H
⊗n
, where H is the
Hadamard gate. Assume the extended computational base V
n
={|0, |1}
n
={|a}, with
|asymbolizing any of the n-qubits base element generated by the n-tensor product |a=
|v
1
⊗|v
2
⊗···⊗|v
n
where v
i
= 0orv
i
= 1(i = 1,...,n). As a general property,
it can be shown that
H
⊗n
|a=
1
√
2
n
V
n
(−1)
a∗b
|b, (16.57)
where |b=|w
1
⊗|w
2
⊗···|w
n
is any base element of V
n
, and a
∗
b is a scalar
defined as:
a
∗
b = v
1
w
1
+ v
2
w
2
+···+v
n
w
n
=
n
i=1
v
i
w
i
. (16.58)
With the tensor-product tools developed in this section, it is proposed as a closing
exercise to establish the property in Eq. (16.57) for the case n = 2, then by induction
for the general case.

330 Quantum bits and quantum gates
16.6 Noncloning theorem
Given a quantum system A,inanystate|ψ, and a second quantum system B,inany
pure state |s, is it possible to duplicate the first state into the second? Such a “cloning”
operation would correspond to the transformation:
|ψ⊗|s→U(|ψ⊗|s) =|ψ⊗|ψ≡|ψ, ψ, (16.59)
where U is a unitary tensor operator. Assume that such an operator U exists and applies
to any state |ψ of A.Let|φ be another state of A such that |φ =|ψ.Wemustalso
be able to duplicate it into B according to:
U (|φ⊗|s) =|φ⊗|φ≡|φ,φ. (16.60)
By linearity of the transformation, we must also have for any state mixture |χ =
λ|ψ+µ|φ of A, where λ, µ are two complex numbers:
U (|χ⊗|s) =|χ⊗|χ≡|χ,χ. (16.61)
If we develop the left-hand side of Eq. (16.61) we obtain:
U (|χ⊗|s) = U (λ|ψ+µ|φ) ⊗|x
= λ|ψ⊗|ψ+µ|φ⊗|φ
≡ λ|ψ, ψ+µ|φ,φ,
(16.62)
while the right-hand side in Eq. (16.61) yields:
|χ⊗|χ=(λ|ψ+µ|φ) ⊗ (λ|ψ+µ|φ)
= λ
2
|ψ⊗|ψ+µλ(|ψ⊗|φ+|φ⊗|ψ) + µ
2
|φ⊗|φ
≡ λ
2
|ψ, ψ+µλ|ψ, φ+µλ|φ, ψ+µ
2
|φ,φ.
(16.63)
Equating Eqs. (16.62) and (16.63) yields
λ(λ − 1)|ψ, ψ+µλ|ψ, φ+µλ|φ,ψ+µ(µ − 1)|φ,φ≡0. (16.64)
Assuming that |ψ, |φ are pure states, the above equation implies that µλ = 0 and,
thus, |χ =|ψ or |χ=|φ. This result means that if there exists an operator U that
can clone two pure states |ψ, |φ, this operator cannot clone any of their mixtures
|χ=λ|ψ+µ|φ, which is a quite restrictive conclusion.
We are then left with the open question: does any cloning operator U exist in the
first place? The answer is straightforward, but it requires one to use the inner product
of states, which is introduced in Chapter 17. Suffice it here to provide the result: there
always exist a unitary operator U capable of cloning a pure state |ψ, or any pair of
pure states |ψand |
¯
ψ(see Chapter 17 for proof). As we have previously seen, however,
such an operator cannot clone the mixture |χ =λ|ψ+µ|
¯
ψ. The key conclusion is
that, except for the limiting case of pure-state pairs, it is not possible to clone quantum
states in the general case. This fundamental result is known as the noncloning theorem.
In the specific case of qubits, the two possible bases of pure states are {|s
1
, |s
2
} ≡
{|0, |1}, {|+, |−}. With our knowledge of quantum gates, it is trivial that we can find
operators capable of “cloning” pure states into each other. Thus the exception about

16.7 Exercises 331
pure states does not weaken in any sense the generality of the noncloning theorem.In
particular, there is no quantum gate capable of executing the equivalent of the classical
FANOUT gate (Chapter 15), for any state other than a pure state.
16.7 Exercises
16.1 (B): Show by two different methods that the Hadamard gate H corresponds to
a unitary transformation.
16.2 (T): Prove the property according to which the three operators R
k
(γ )(k =
x, y, z) rotate any qubit |q on the Bloch sphere by an angle γ about the axis k,
in the counterclockwise direction.
16.3 (B): Prove the following properties of the rotation operators:
R
i
(2θ)R
i
(−2θ) = I
[R
i
(2θ), R
j
(2θ
)] =−2iε
ijk
sin θ sin θ
+ sin(θ −θ
)
[R
i
(2θ),σ
j
] = 2ε
ijk
σ
k
sin θ.
16.4 (B): Determine the parameters n,θ associated with any unitary transformation
U according to the definition:
U = exp[i( n · σ )θ ].
Clue: use the generic definition of unitary matrices for U :
U = e
iδ
ab
−
¯
b
¯
a
.
16.5 (M): Prove that any 2 × 2 unitary matrix U can be expressed from the two
rotation operators R
y
, R
z
according to the product:
U = e
iδ
R
z
(α)R
y
(β)R
z
(γ ),
where α, β, γ , δ are real numbers (Euler’s theorem).
16.6 (M): Considering the quantum-gate circuit
x
x
xx
x
xx
x
x
x
x
x
A
CNOT
A
CNOT
B
CNOT
show first that the matrix of the intermediate B
CNOT
gate takes the form
B
CNOT
=
1000
0001
0010
0100
,
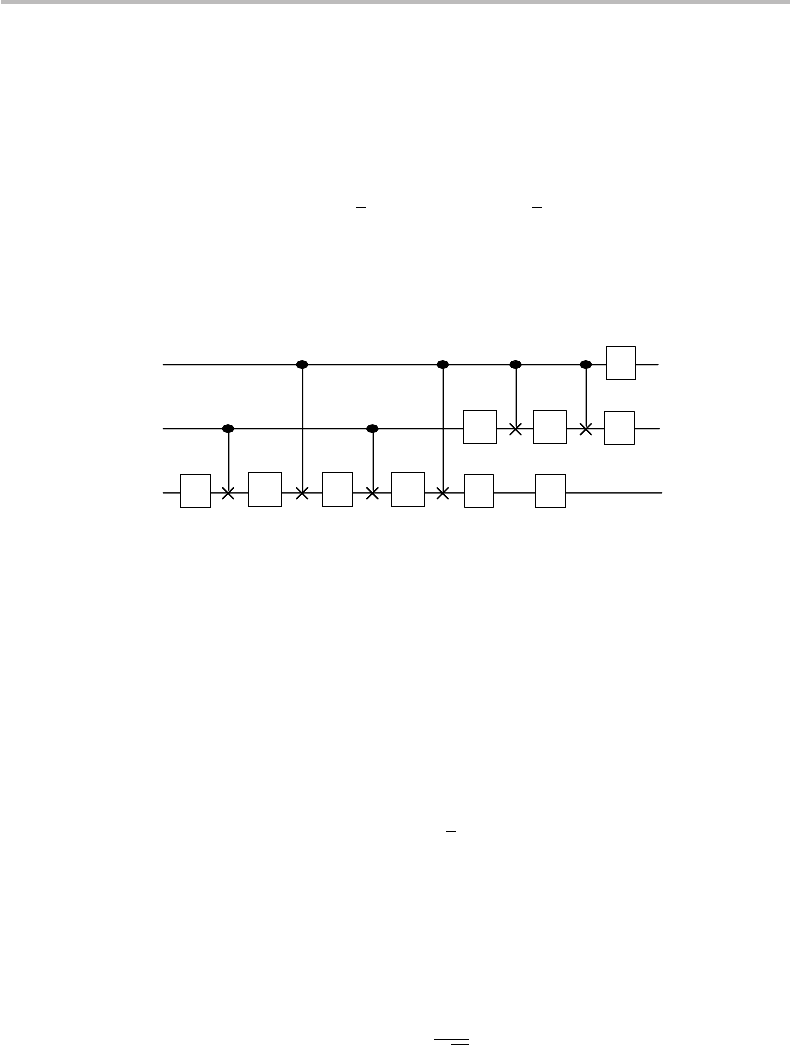
332 Quantum bits and quantum gates
assuming the computational base {|0|0, |0|1, |1|0, |1|1}. Then prove by
matrix multiplication that the circuit is equivalent to a CROSSOVER or SWAP
gate.
16.7 (M): Analyze the action of a CNOT gate with control qubit |ain a superposition
of states (assume |a=γ |0+δ|1 and |x=α|0+β|1). Consider then the
two cases γ = δ = 1/
√
2 and γ =−δ = 1/
√
2 for the control qubit. What are
the possible output states? Show that the same result is obtained with all inputs
in pure states and with a Hadamard gate placed on the control input path.
16.8 (T): Prove that the quantum circuit
Y
,
Z
H
T
+
T
+
T
T
H
+
T
+
T
S
T
HH
TT
+
T
+
T
+
T
+
T
TT
HH
+
T
+
T
+
T
+
T
SS
TT
which includes Hadamard gates (H ), ±π/4-phase gates (T, T
+
), and a single
π/2-phase gate (S), is an equivalent realization of a CCNOT or Toffoli gate.
16.9 (B): Given the Pauli matrices Y, Z , calculate the tensor product Y ⊗ Z.Given
two qubits |a, |b and their tensor product |a⊗|b, show that
Y ⊗ Z (|a⊗|b) = Y |a⊗Z |b.
16.10 (T): Given the computational base V ={|0, |1} and the Hadamard operator
H, show that the two-fold tensor product H
⊗2
= H ⊗ H satisfies
H
⊗2
|a=
1
2
V
n
(−1)
a∗b
|b,
where |a=|v
1
⊗|v
2
and |b=|w
1
⊗|w
2
are any elements of V
2
(with
v
i
,w
j
= 0, 1) and
a
∗
b = v
1
w
1
+ v
2
w
2
.
Then prove by induction that, in the general case,
H
⊗n
|a=
1
√
2
n
V
n
(−1)
a
∗
b
|b,
with
a
∗
b = v
1
w
1
+ v
2
w
2
+···+v
n
w
n
=
n
i=1
v
i
w
i
.

17 Quantum measurements
This chapter is concerned with the measure of quantum states. This requires one to
introduce the subtle notion of quantum measurement, an operation that has no counterpart
in the classical domain. To this effect, we first need to develop some new tools, starting
with Dirac notation, a formalism that is not only very elegant but is relatively simple
to handle. The introduction of Dirac notation makes it possible to become familiar with
the inner product for quantum states, as well as different properties for operators and
states concerning projection, change of basis, unitary transformations, matrix elements,
similarity transformations, eigenvalues and eigenstates, spectral decomposition and
diagonal representation, matrix trace and density operator or matrix. The concept of
density matrix makes it possible to provide a very first and brief hint of the analog of
Shannon’s entropy in the quantum world, referred to as von Neumann’s entropy,tobe
further developed in Chapter 21. Once we have all the required tools, we can focus
on quantum measurement and analyze three different types referred to as basis-state
measurements, projection or von Neumann measurements, and POVM measurements.
In particular, POVM measurements are shown to possess a remarkable property of
unambiguous quantum state discrimination (UQSD), after which it is possible to derive
“absolutely certain” information from unknown system states. The more complex case
of quantum measurements in composite systems described by joint or tensor states is
then considered. Although of a more abstract and formal character than any previous
ones, this chapter is crucial to the understanding of the rest of these chapters, which are
concerned with the manipulation of qubits. This is not only because of the importance of
being comfortable with the Dirac formalism, but also of the need to have conceptually
assimilated the basics of quantum measurement.
17.1 Dirac notation
In this section, I shall introduce so-called Dirac notation, which are used in quantum
mechanics. When compared with the basic math formalism used in engineering, Dirac
notation looks quite esoteric, if not highly involved and complex. But as we shall see, such
notation is straightforward to assimilate, and quite easy to handle after familiarization.
Dirac notation is used to recapitulate the basic properties of linear operators and their
action on quantum states (here, qubits), which leads to a simple formalization of the
concept of quantum measurement.

334 Quantum measurements
In Chapter 16, we defined the qubit as a 2D vector noted |q. In the orthonormal
basis of pure states V ={|0, |1}, the qubit has complex coordinates α, β, so that
|q=α|0+β|1. As we have seen, higher-dimension qubits can be defined from the
extended basis V
n
={|x}, where |xis the nth tensor product of the pure state |δ
i
=|0
or |1, namely:
|x=|δ
1
⊗|δ
2
⊗···⊗|δ
n
≡|δ
1
,δ
2
,...,δ
n
≡|δ
1
δ
2
···δ
n
,
(17.1)
where the two equivalent notations in the right-hand side can be used for lightening
purposes. In this extended space, the qubit |q can, thus, be expanded into
|q=
x∈V
n
x|x, (17.2)
where x represents the complex coordinate of |q with respect to the n-qubit basis
element |x.
Regardless of any basis dimension n, the qubit or vector |q is also referred to as a
“ket.” Actually, the ket represents the Dirac notation for a quantum state in the space
defined by V ={|0, |1}, which is referred to as Hilbert space. Here, we do not need
to elaborate further on the notions of quantum state (as related to the physical world)
and of Hilbert space (as defining the continuum of such quantum states). As it turns out,
the concept of qubit as a vector, rather than as a quantum state, even as representing an
oversimplification, is accurate and wholly sufficient to grasp Dirac formalism.
Inner product
In a 2D vector space, the scalar product of two vectors x = (x
1
, x
2
) and y = (y
1
, y
2
)is
defined as the real number x · y = x
1
y
1
+ x
2
y
2
. In particular, the self-product x · x =
x
2
1
+ x
2
2
≡|x|
2
corresponds to the vector’s length or modulus. In the qubit space V
(meaning “defined by any orthogonal basis such as V ”), we can introduce the concept of
the inner product of two qubits, |q=α|0+β|1 and |q
=α
|0+β
|1 according
to:
|q·|q
=¯αα
+
¯
ββ
, (17.3)
where ¯α,
¯
β are the complex conjugates of the coordinates α, β, respectively. In particular,
we have |q·|q=|α|
2
+|β|
2
, which as a real number, represents the modulus of the
qubit |q. In vector notation, Eq. (17.3) can be written as a line-vector–column-vector
product:
|q·|q
=|q
T
|q
=(¯α,
¯
β)
α
β
= ¯αα
+
¯
ββ
, (17.4)
where
|q
T
is the conjugate-transposed of |q. Here is a first opportunity to show
how Dirac notation comes in handy. Indeed, define the “bra” q| as representing the

17.1 Dirac notation 335
conjugate-transposed vector |q
T
. With this notation, Eq. (17.4) becomes the “bra-ket:”
q|q
=¯αα
+
¯
ββ
(17.5)
And, hence, for the qubit modulus, q|q=|α|
2
+|β|
2
. As another property, we note
from Eq. (17.5) that q|q
=q
|q, namely that the inner product of qubit states is
noncommutative, unlike the scalar product of 2D vectors with real coordinates.
As we shall see next, there is more in the “bra” notation than just a convenient way to
express the inner product between two qubit states. Indeed, consider n-qubits |q, |q
in
the space V
n
, with, for |q
, the expansion in Eq. (17.2) and, for the bra, q| (consistently
with definition):
q|=
x∈V
n
¯
xx|. (17.6)
We can now develop the inner product q|q
according to
q|q
=
3
x∈V
n
¯
xx|
43
x
∈V
n
x
|x
4
=
x∈V
n
x
∈V
n
¯
xx
x|x
. (17.7)
Since |x, |x
are pure states from the orthonormal basis V
n
,wehavex|x
=δ
ss
where δ
ss
is the Kronecker symbol (δ
ss
= 1forx = x
and δ
ss
= 0 otherwise). Hence
the explicit definition of inner product when the two qubits are expressed in the same
basis V
n
:
q|q
=
x∈V
n
x
∈V
n
¯
xx
δ
xx
. (17.7)
Which, for |q
=|q, reduces to the modulus:
q|q=
x∈V
n
|x|
2
. (17.8)
In particular, effecting a left product by x| to Eq. (17.2) we have
x|q=
x
∈V
n
xx|x
=
x
∈V
n
xδ
xx
= x, (17.9)
which shows that, expectedly, x|q=x is the projection of |q over the pure state |x.
Substituting this result into the definition in Eq. (17.2), we obtain
|q=
x∈V
n
x|x=
x∈V
n
x|q|x≡
x∈V
n
|xx|q, (17.10)
which represents another way of expanding |q over the basis V
n
.
In Chapter 16, we have shown that it is generally not possible to “clone” quantum
states, a property referred to as the noncloning theorem. As was mentioned without

336 Quantum measurements
proof, the only exceptions to this theorem concern any pure state, or any pair of pure
states. With the inner product introduced above, it is quite easy to show this.
1
Projection operators
In view of the expansion of |q in Eq. (17.10), we can introduce U
x
=|xx| as the
operator projecting any qubit onto the state |x. To show this, we first observe that
U
x
|x=(|xx|)|x=|xx|x=|xδ
xx
≡|x (17.11)
and
U
x
|q=(|xx|)
x
∈V
n
x
|x
=
x
∈V
n
x
|xx|x
=|x
x
∈V
n
x
δ
xx
≡ x|x,
(17.12)
which shows that |x is invariant by U
x
and also that |q is projected on its basis
component x|x. With such a definition of projector operator, we also have from
Eq. (17.10):
|q=
3
x∈V
n
|xx|
4
|q, (17.13)
from which we obtain
x∈V
n
|xx|=I. (17.14)
The above property, which is referred to as the completeness (or closure) relation,
expresses the fact that the complete sum of all projection operators over the pure states
of V
n
is the identity operator. More generally, a unitary operator U is a projector if it
satisfies the property U
2
= U (projecting twice is the same as projecting once). In the
case of U
x
=|xx|, we have, indeed,
U
2
x
= U
x
U
x
= (|xx|)(|xx|)
=|xx|xx|=|xδ
xx
x|=|xx|≡U
x
(17.15)
1
Referring to Section 16.6, given three pure states |s, |ψ, |φ, we assume a unitary operator U capable to
achieve the following cloning transformations:
U(|ψ⊗|x) =|ψ⊗|ψ,
U(|φ⊗|s) =|φ⊗|φ.
Taking the inner product of the two right-hand sides and using the properties U
+
U = I and s|s=1,
yields:
(φ|⊗s|)U
+
U(|ψ⊗|x) = (φ|⊗φ|)(|ψ⊗|ψ) ↔φ|ψs|s
=φ|ψφ|ψ↔φ|ψ=φ|ψ
2
,
which shows that either φ|ψ=1orφ|ψ=0, corresponding to |φ=|ψ or |φ, |ψ being orthogonal
states.
