Давнис В.В. Прогнозные модели экспертных предпочтений
Подождите немного. Документ загружается.

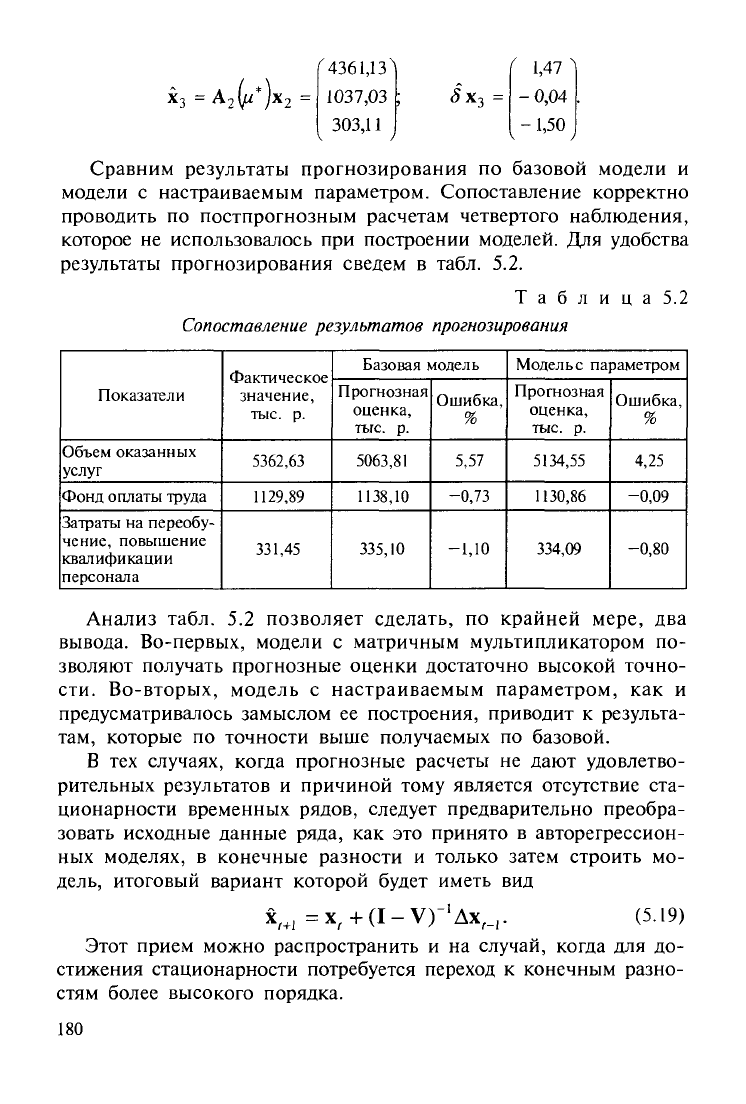
>("*)
х
2 =
4361,13
1037,03
303,11
f
5x-i =
1,47 ^
-0,04
-1,50
Сравним результаты прогнозирования по базовой модели и
модели с настраиваемым параметром. Сопоставление корректно
проводить по постпрогнозным расчетам четвертого наблюдения,
которое не использовалось при построении моделей. Для удобства
результаты прогнозирования сведем в табл. 5.2.
Таблица 5.2
Сопоставление результатов прогнозирования
Показатели
Объем оказанных
услуг
Фонд оплаты труда
Затраты на переобу-
чение, повышение
квалификации
персонала
Фактическое
значение,
тыс.
р.
5362,63
1129,89
331,45
Базовая модель
Прогнозная
оценка,
тыс.
р.
5063,81
1138,10
335,10
Ошибка,
%
5,57
-0,73
-1,10
Модельс параметром
Прогнозная
оценка,
тыс.
р.
5134,55
1130,86
334,09
Ошибка,
%
4,25
-0,09
-0,80
Анализ табл. 5.2 позволяет сделать, по крайней мере, два
вывода. Во-первых, модели с матричным мультипликатором по-
зволяют получать прогнозные оценки достаточно высокой точно-
сти.
Во-вторых, модель с настраиваемым параметром, как и
предусматривалось замыслом ее построения, приводит к результа-
там, которые по точности выше получаемых по базовой.
В тех случаях, когда прогнозные расчеты не дают удовлетво-
рительных результатов и причиной тому является отсутствие ста-
ционарности временных рядов, следует предварительно преобра-
зовать исходные данные ряда, как это принято в авторегрессион-
ных моделях, в конечные разности и только затем строить мо-
дель,
итоговый вариант которой будет иметь вид
V+1
= х, + (1-УГДх_,.
(5.19)
Этот прием можно распространить и на случай, когда для до-
стижения стационарности потребуется переход к конечным разно-
стям более высокого порядка.
180

5.3.
Модель с адаптивным матричным
предиктором
Идеи, лежащие в основе построения адаптивного пре-
диктора, по сути, ничем не отличаются от тех, которые изложе-
ны в предыдущей главе, хотя детали имеют свою специфику.
Чтобы понять эту специфику, опишем не только модель, но и
процедуру ее построения.
Особенность такой модели заключается в том, что ее матрич-
ный предиктор строится в два этапа. На первом этапе определя-
ется начальное приближение, а на втором — организуется про-
цесс обучения мультипликатора в виде рекуррентной процедуры
постпрогнозных расчетов. С этой целью выборочное множество
наблюдений делится на две части. Пусть & (0
>
2) первых наблю-
дений используются для нахождения начальных значений. Кроме
того,
в рассмотрение вводится матрица, определяющая соотноше-
ние прямых и косвенных темпов приростов
М =
( м (1-м) •
(1-м) м •
• (1-м)
• (1-м)
,(1-м) 0-м)
и матрица весовых коэффициентов
М
(5.20)
W
w,.
ИЛ,
W W.
я 2
ИЛ.
W
1
J
(5.21)
определяемая либо по соответствующим коэффициентам корреля-
ции, либо с помощью экспертного оценивания, либо в соответ-
ствии с некоторой гипотезой (например, значимость равномерно
распределена по показателям).
При заданном начальном значении мультипликатора А,, на-
строенных параметрах ц* и а* и известной матрице W адаптив-
ная модель записывается следующим образом:
Ч+\
A
t
x
t
;
(5.22)
181

л/+1 _
X
l+
ij
X
t
_
V ~
X
t+lj
v
t+l
=
Hi
Л/
+ 1
', j
=
ln;
;
A
t+l
=(l-M^W*\
t+l
)~
l
A
/+1
= a"K
t
+ (l
-
a*)A,
+
,A,.
(5.23)
(5.24)
(5.25)
(5.26)
С помощью формулы (5.23) рассчитываются элементы матри-
цы корректирующих темпов прироста
Y
t+l
,
которая использует-
ся для построения корректирующего мультипликатора (5.25). Если
в качестве А
ж
взять произведение корректирующего и текущего
мультипликаторов А,
+1
А
Г
то расчетное значение х,
+1
в точнос-
ти совпадет с фактическим значением вектора показателей х,
+1
.
Однако учитывая, что основное назначение мультипликатора А
ж
— прогноз на период / + 2, его значение комбинируется из А, и
A
f+1
A
r
, причем параметр а, с помощью которого осуществляет-
ся комбинирование, является настраиваемым по критерию мини-
мизации, например, суммарной прогнозной ошибки.
Модель (5.22)—(5.26) записана в предположении, что началь-
ное значение мультипликатора А, и оптимальные значения пара-
метров ц* и а* известны, а сами процедуры их получения не
описывались ранее, поэтому логично привести их алгоритмичес-
кое описание.
Процедура построения начального
приближения:
1.
Расчет текущих значений прямых и косвенных темпов при-
роста показателей
,' _
X
ii ~
X
i-\i
V
V~
x
' i,7=l, я, / = 1,0. (5.27)
2.
Определение геометрических средних значений прямых и
косвенных темпов прироста показателей за период /
(5.28)
182

3.
Формирование матрицы средних темпов прироста показате-
лей за период 0
V
e=|KI
(5-29)
4.
Построение начального приближения мультипликатора для
t = Q
A, =(l-M*W*V,)
_1
. (5.30)
Процедура
настройки
параметров:
1.
Определение шага изменения настраиваемых параметров h
h = S,
где 8 — достаточно малое положительное число.
2.
Присвоение начальных значений параметрам
ц* =0; а* = 0; ц
=
-8
«критерию z(u*,a*)=Q,
где Q — достаточно большое положительное число.
3.
Изменение текущего значения fi
JJ.
=
ц
+
8
и проверка на выполнение неравенства
/л >
1.
Если неравенство выполняется, то настройка параметров заверша-
ется.
4.
Присвоение начального значения параметру а
а
=
-8.
5. Изменение текущего значения а
а
=
а
+
8
и проверка на выполнение неравенства
а
>
1.
Если неравенство выполняется, то выполняется п.З.
6. Установка счетчика
t = k -1.
7.
Присвоение начального значения критерию
Z(n,
а) = 0.
8. Изменение счетчика
t = t + 1
и его проверка: если t > Т, то выполняется
п.
16.
9. Вычисление постпрогнозной оценки
Х
<+1
_
^(
Х
г-
183

10.
Расчет критерия
Z,
+1
(jU,a)=maxjx,
+1
, -
x
l+h
[
11.
Определение суммарного критерия по всему периоду обу-
чения
Zip.,
a)= Z(/i, a)+Z
t+1
(fi, a).
12.
Вычисление корректирующих темпов прироста
X
t+lj
13.
Формирование матрицы корректирующих темпов прироста
V
ll"'+i||
,+1 =
\П Г
14.
Построение корректирующего мультипликатора
A,
+1
= (l-M* *W*V,
+1
)~\
15.
Определение текущего мультипликатора для момента вре-
мени ?+1
А,
+1
=а*А, + (L-«*)A,
+1
A,
и переход на п.8.
16.
Сравнение текущего значения критерия с его текущим
оптимальным значением: если Z([i, a) <Z(n*, а*), то
ц* = /л, а" = а ; Z\fi*, а*
) =
Z(u, а).
17.
Переход на п.5.
Описанные процедуры построения начального приближения
мультипликатора и настройки параметров достаточно универсаль-
ны и могут использоваться при построении любых модификаций
базовой модели с мультипликатором.
Для примера, иллюстрирующего построение модели с адаптив-
ным матричным мультипликатором, обратимся, как и в преды-
дущих примерах, к данным табл. 5.1.
В качестве начального значения адаптивного мультипликатора
используем
А
2
(ц*),
поскольку процедура построения начального
значения приведет к аналогичному результату.
Далее, при ранее определенном //, рассчитываем прогнозную
184

оценку и находим ошибки, которые принимаются за корректиру-
ющие отклонения
' 65,0858 ^
- 0,4209
А
3
= (l-M* *W*V
3
)~' =
Дх
3
= х
3
- А
2
(и*)х-
- 4,4856
По этим отклонениям строим корректирующий мультипликатор
1,0134
0,0032 0,0109
Л
0,0000 0,9996 - 0,0001
-0,0001 -0,0002 0,9867
;
и при начальном значении А = 0,1 получаем текущее значение
адаптивного мультипликатора
("1,1575 0,0378
0,135
О
A
3
(U*,A)=AA
2
(U*)+(1-A)A
3
A
2
(U*) = 0,0013
1,0800
0,0174
0,0004 0,0016
1,0920
параметр которого А настраивается по относительной ошибке
' 2,98
Л
5х
4
= -0,05
0,55
постпрогнозной оценки четвертого наблюдения
/"5203,04
Л
Х
4
= А
3
(и*,я)х
3
1130,45
329,63
Так как оптимальное А* оказалось равным начальному значе-
нию,
т.е.
А*
= 0,1, то и окончательное значение мультипликатора
не меняется, т.е. A
3
(/i*, A*) = А
3
(^*, А).
Расчеты прогнозных оценок для пятого периода дают следу-
ющие результаты:
х
5
= А
3
(
/
и*,А*)х
4
=
6294,93
1232,97
366,03
5х,
( 2,10
-5,24
-5,20
185

Необходимо отметить, что если адаптивное свойство не улуч-
шает прогностическую точность модели, то параметр Я в резуль-
тате настройки принимает значение, равное единице, и адаптив-
ная модель вырождается в статическую.
В рассмотренной процедуре реализована только схема коррек-
тировки по ошибке предсказания. Выбор именно этой схемы в
основном связан с ограниченным объемом выборочных данных,
используемых для построения адаптивной модели. Применение
адаптивных принципов при попытке осуществления прогнозных
расчетов на основе коротких временных рядов, безусловно, имеет
смысл. Однако в тех случаях, когда все же существует некоторая
история прогнозируемого процесса, желательно чтобы вся инфор-
мация с учетом распределения ее значимости была учтена при
построении прогнозных оценок. В связи с этим замечанием име-
ет смысл в адаптивном механизме модели использовать принцип
экспоненциального старения данных.
Применяя те же самые обозначения, экспоненциально взве-
шенный матричный предиктор может быть записан следующим
образом:
х, = (1-а)А,х,_, +а(1-а)А
2
х,_
2
+---
+
а
/,ч
А
/
,х,_
р
, (5.31)
где А^ — матричный предиктор, построенный по отклонениям
наблюдений х, и х
гк
, причем для любого к имеем
х, =А
к
х,_
к
. (5.32)
Другими словами, предиктор А^ реализует расчет по средним за
к периодов темпам роста. Таким образом, темп роста, задаваемый
предиктором, складывается из средних темпов роста за р, р
—
1, ...,
2,
1 периодов. Весовые коэффициенты каждой составляющей
результирующего темпа роста распределены по экспоненциальному
закону с затуханием от темпа роста, определенного по двум пос-
ледним наблюдениям, до усредненного по всем наблюдениям.
Параметр экспоненциального сглаживания а настраивается
подбором по постпрогнозным ошибкам, точно так же, как это
делалось в предыдущей модели. Сохраняется и принцип адаптив-
ной корректировки. По вновь поступившему наблюдению строит-
ся матрица (5.25), с помощью которой корректируется текущий
предиктор. Формально это выглядит следующим образом:
186

х, = /}[(1-а)А,х,_,
+
а(1-а)А
2
х,_
2
+--
+
а
р [
A
p
x
t
_
p
]
+
+
(1-/3)А,
+1
[(1-а)А,х,_,
+
а(1-а)А
2
х,_
2
+ --- +
а
р
~
1
А
р
х,_
р
].(5.зз)
В тех ситуациях, когда позволяют данные, рекомендуется
строить модель с адаптивным механизмом экспоненциального ста-
рения данных, так как с ее помощью удается получить более на-
дежные оценки.
5.4. Матричная модель с разделенными
переменными
В целом, числовые примеры показали практическую
реализуемость моделей с настраиваемым параметром и адаптивным
мультипликатором. Разработанными моделями не исчерпываются
все возможности, заложенные в принципы построения мультипли-
катора. Приоткрыть эти возможности позволяет модель с разде-
ленными переменными, представляющая собой еще одну специ-
фическую модификацию базовой модели.
По сути, она похожа на модель многофакторного регрессион-
ного анализа. Ее переменные разбиты на две группы. Перемен-
ные первой группы будем называть целевыми, а второй — ресурс-
ными. Целевые переменные представляют собой показатели, ха-
рактеризующие результаты функционирования экономического
объекта, а ресурсные — потенциальные возможности этого же
объекта. Считая, что все показатели упорядочены таким образом,
что вначале стоят целевые переменные, вектор которых обозначим
через х,
1;
а в конце — ресурсные х
й
, запишем базовую модель
(5.6) в виде
(х >
\
,z
)
=
(х >
+
Ml
v
12
^21 Уг
2у
(х \
Х*о
V
JL
)
Выполнив умножение, получаем две системы уравнений
Х
/1
= Х
г-11
+
*11
Х
П
+
М2
Х
Г2>
Х
/2
= X
r-12
+
*
21
X,! +V
2
2X,
2
.
Проведя перегруппировку, имеем
х
п ~ »и
х
(1
= х
г-п
+
*
12
х,
2
;
х
/2
—
V
22
x
/2
= х,_
12
+
\
2
1
х
-
гГ
(5.35)
(5.36)
(5.37)
(5.38)
187

Решая каждую из этих систем, получаем
х„ =(I-V
11
)"
1
(x
f
_„ +V
l2
x,
2
);
х,
2
=(I-V
22
)"
1
(x,_
12
+V
21
x
fl
).
(5.39)
(5.40)
Первое уравнение определяет значения целевых переменных
через запаздывающие значения этих же переменных и ресурсные
переменные, а второе — значения ресурсных переменных через их
лаговые значения и целевые переменные.
С помощью этой модели решаются как бы две взаимодвой-
ственные задачи. Смысл первой из них в том, что при известных
значениях ресурсных показателей определяются значения целевых
показателей, т.е. (5.39), по сути, является своеобразным вектор-
ным аналогом уравнения множественной регрессии. С помощью
второго уравнения решается обратная задача: по заданным значе-
ниям целевых показателей определяются значения ресурсных,
обеспечивающих достижение целевых. Следует отметить, что воз-
можность решения обратной задачи выгодно отличает эту модель
от моделей регрессионного анализа, так как расширяет сферу ее
прикладного использования. На основе этого математического
аппарата можно построить методику, позволяющую сформировать
допустимые варианты плана, и тем самым проиллюстрировать
возможность переноса идеи альтернативности стратегического
выбора в практическую плоскость.
Используя все те же данные табл. 5.1 для построения модели
с разделенными переменными, положим, что объем оказанных
услуг х, и фонд оплаты труда х
2
являются целевыми показателя-
ми,
а затраты на переобучение и повышение квалификации пер-
сонала х
3
— ресурсными. В соответствии с таким разделением пе-
ременных матрицу косвенных темпов прироста V
2
разобьем на
четыре части, из которых для дальнейших расчетов потребуются
только две:
V„ =
О 0,2755
0,0105 0
Получив обратную матрицу
A
u
=(l-V
u
y
l
0,9669
0,1449
(1,0029 0,2763^
0,0105
1,0029

х
3
- А
и
|х
2
+
V
12
x
33
J —
х\
= 271,02 + (0,0038 0,0151)
= 303,54.
рассчитаем прогнозные оценки для третьего периода *з =
(А'З
i
>-*32)
в зависимости от ожидаемых в этом же периоде затрат на пере-
обучение и повышение квалификации персонала:
М330,68'
1039,55
С помощью этой модели можно изучать динамику прогнозных
оценок в зависимости от изменения плановых затрат перспектив-
ного периода.
Для случая, когда по заданным значениям целевых показате-
лей х
3
' требуется определить уровень ресурсных х
3
, обеспечива-
ющих достижение заданных значений целевых, модель выглядит
следующим образом:
x
3
2
= (l-V
22
)-'(x2
+
V
21
x
3
).
Так как в рассматриваемом примере (I-V
22
)=l, то расчеты
упрощаются и искомое значение ресурсного показателя равно
'4426,22
Л
1036,61
Расчеты показали, что, действительно, с достаточно большой
точностью можно решать как прямую задачу по определению зна-
чений целевых показателей по ресурсным, так и обратную — рас-
чет уровня ресурсного показателя, требуемого для достижения
заданных значений целевых.
В разработанной модели с разделенными переменными ис-
пользуется мультипликатор базовой модели (5.6). Естественно,
аналогичная модель может быть получена и с адаптивным матрич-
ным мультипликатором. Однако мы опускаем отдельное рассмот-
рение подобной модели, так как ее построение не вызывает осо-
бых затруднений, если руководствоваться принципами, заложен-
ными в (5.22)—(5.26).
5.5. Вычислительная схема комбинированных
прогнозных расчетов для многомерных
процессов
Идеи, на основе которых была построена модель пе-
реходных процессов, позволяющая комбинировать в прогнозных
оценках фактографическую и экспертную информацию, могут
практически без изменений использоваться при решении задач
189
