Давнис В.В. Прогнозные модели экспертных предпочтений

Подождите немного. Документ загружается.

4.5. Адаптивное моделирование переходных

процессов в комбинированных прогнозах

Комбинируя экстраполяционные и экспертные прог-

нозные оценки, мы полагаем, что доверие к этим оценкам раз-

ное и, более того, изменяется с изменением величины упрежде-

ния. Ключевой проблемой в реализации идеи такого комбиниро-

вания является задача моделирования переходных процессов. Вы-

полнение этой задачи должно быть устроено таким образом, что-

бы степень доверия комбинированным прогнозным оценкам оста-

валась на максимально возможном уровне. Разрешение этой про-

блемы прежде всего связано с формулировкой экстремальной за-

дачи, в функционале которой предусматривалась бы возможность

построения адаптивного механизма, обеспечивающего получение

комбинированной прогнозной траектории с требуемым свойством.

Для реализации этой идеи положим, что в результате обработ-

ки исходных данных и дополнительных исследований мы имеем

две последовательности прогнозных оценок {у.} и {у.}. Первая из

них является итогом экстраполяционных расчетов и с течением

времени степень доверия к ним снижается, а вторая — эксперт-

ного оценивания, к результатам которого степень доверия с уве-

личением глубины упреждения возрастает. Тогда экстремальную

задачу, соответствующую этим предположениям, можно записать

следующим образом:

Ц)

Argmin £A V^[y. -х,.В(г)]

7=1

где А — параметр, регулирующий степень доверия комбинирован-

ному прогнозу в зависимости от глубины упреждения (0 <

< 1);

а — параметр экспоненциального сглаживания (0 < а < 1);

•

(l,

X\j,

/'•••'

mj ) — вектор-строка значений факторов в

момент времени j; в(?) =

(t),

{

(t),..., b

(t)) — вектор-столбец

коэффициентов адаптивной модели.

Первое слагаемое функционала задачи (4.57) представляет со-

бой дважды взвешенную сумму квадратов отклонений расчетных

значений от данных экстраполяционной траектории. С помощью

(4.57)

160

параметра а в нем реализуется механизм затухающей памяти ,

касающийся старых тенденций, а с помощью параметра Я — ме-

ханизм, позволяющий постепенно с течением времени снижать

долю "присутствия" экстраполяционной траектории в комбиниро-

ванной.

Второе слагаемое устроено аналогично первому. В нем мини-

мизируются отклонения расчетных значений от данных экспертных

ожиданий. Причем параметр Я служит для постепенного увеличе-

ния степени влияния экспертных оценок на тенденции, реализу-

емые в комбинированной траектории.

Дифференцируя выражение в фигурных скобках (4.57) по В(?)

и приравнивая результат к нулю, получаем систему из (т + 1)-го

уравнения

-2XrV-^,-x

.B(r)]x'

7=1

-2t(l-^)a^b

-x

;

B(r)]x;.=0.

7=1

(4.58)

Преобразуем систему, перенеся в правую часть те слагаемые,

которые не содержат оцениваемых параметров

ta-

jXjB(t)= ХА'сГ'*^.

t(l-А0сГ

;

х'Д

7=1 7=1 7=1

(4.59)

После перегруппировки систему (4.59) можно записать следу-

ющим образом:

ta'-V.x,.B(0= £a

-Jxfyy

+tl-A.

7=1 7=1

Если ввести обозначения

(4.60)

Y,=

Уг

У')

х,=

1 х

*21

г1

2п

tm J

(4.61)

161

L,=

V-'

о •

•

0 •

- о]

• 0

•• a

; л,=

0 •

• •

•• 0

•• A'

(4.62)

то в матричной форме система (4.60) перепишется в виде

(X;L,X,)B(/)=X;L,[A,Y, +(I-A,)Y,] • (4-63)

Ее решение можно представить как

B(t)=(X'

[

{x'

(l-A

]}. (4.64)

Чтобы перейти к рекуррентной процедуре последовательного

оценивания коэффициентов адаптивной рефессии, будем считать

последнее наблюдение вновь поступившим и представим (4.64) в

виде

в(0=(ож;_

х,_

+х;

,)г

х{аХ;_

[л

+(1-Л,_

)¥

_,]+х;[1'

+^-А')?

]}(4.65)

Обозначим

C^X^L^X,., (4.66)

и, используя формулу рекуррентного обращения матриц Шерма-

на — Мориссона, которая в нашем случае имеет вид

(с,_

х;х,Г

сгЛ-^^-

х,сг>;+1'

перепишем (4.65) следующим образом:

в(/)

1 ^,-1 _ 1 C

_iX

'-1 7 1

« a

c;W

(

{ay

k-iYM

+ (I

Л,-1

ft-J+ *& Ч

+ (l

'),,]}

(4-67)

162

Выполнив

(4.67) умножение

некоторую перегруппировку

результатов перемножения, можем записать

в(/)=в

(/ -1)

c,-i

; tyy

+ (i

л'

} -

_l CrVix C,-i,

^;_

|Lb|

[

|tb|

(I-A,_,)Y,_|].

После несложных преобразований получаем

(4.68)

B(f) = B(f-l) + -C

-Vf

C^ix', +

r'v'

/^7 — 1 / —1

' ^

\Xy

+(l-X')y]-

x,B(r-l)

(4.69)

Приведение

общему знаменателю

квадратной скобке позво-

ляет записать (4.69) следующим образом:

B(r) = B(/-l)

^V^+(l-A')^]-

Л-г-1

Hv'

>£—*

B(r-l).

r-i

' , • ^ '•

(4.70)

Окончательная формула для рекуррентного вычисления коэф-

фициентов В(/) приобретает вид

B(t) =

-l)

^^{\Xy

(l-X)y

B(t-l)}. (4.71)

Л"7-1

Начальные значения В(0)

определяются по данным рет-

роспективного периода

помощью МНК. Оптимальное значение

параметра сглаживания

подбирается

использованием пост-

прогнозных расчетов

на

контрольной выборке,

качестве кото-

рой, как правило, используются последние наблюдения ретрос-

пективного ряда. Задача подбора оптимального значения парамет-

163

pa Я не может быть решена по аналогии с параметром а, так как,

в принципе, нельзя получить данные для сравнения с постпрогноз-

ными расчетами. Четких рекомендаций по его подбору нет. Од-

нако если предположить, что степень доверия экстраполяционным

данным в начале упреждающего периода равна степени доверия

рациональным ожиданиям в конце упреждающего периода, то

значение параметра Я определяется из уравнения 1

—

= I, где

т — длина периода упреждения. В тех случаях, когда абсолют-

ным доверием пользуется только одна из траекторий, Я принимает

соответственно значения 0 или 1.

Таким образом, в общем виде адаптивная модель для расчета

комбинированной траектории выглядит следующим образом:

=*,«т

£(r + i) = £(/)+

~~ГГ {(^ж

+ (l

- А'

Ы-

х,

В(/)};

(4.73)

/+i^?

/+i

+ a

4+1

Q-1 Ц

!+l

t+l^r

Г + 1*-Т

/+1

+СС

(4.74)

Модель (4.72)—(4.74) можно применять для построения комби-

нированных прогнозных оценок в тех случаях, когда в качестве

экспертной траектории используются непосредственно числовые

значения, получившие в результате сравнения с другими возмож-

ными вариантами ожидаемых значений экспертное предпочтение.

Если же считать, что в своих оценках эксперты руководствовались

некой моделью и в комбинированном прогнозе следует учесть не

значения, а тенденцию, в соответствии с которой эти значения

были сформированы, то возникает проблема восстановления этой

тенденции. Такая ситуация обычна для регрессионного анализа и

при наличии достаточных информационных возможностей эксперт-

ные оценки аппроксимируются регрессионным уравнением

=x,B,

t = lt, (4.75)

которое используется при построении комбинированной модели.

Модель, ориентированная на использование тенденций, в со-

ответствии с которыми формировались экспертные ожидания,

естественно, должна отличаться от только что рассмотренной. Это

164

отличие касается, прежде всего, второго слагаемого

ее

квадра-

тичного функционала. Оно, по идее, должно представлять собой

дважды взвешенную сумму квадратов отклонений расчетных зна-

чений от соответствующих значений, определяемых построенным

уравнением регрессии (4.75),

саму экстремальную задачу мож-

но записать

виде

В (/) = Argmin

a'~

[у,-

В(/)]

i(l-A;)a'-J[xjB-XjB(t)}

(476)

При записи этого функционала использованы

те

же самые

обозначения, что

и в

функционале (4.57), кроме вектора

В,

который представляет собой коэффициенты регрессионного урав-

нения (4.75).

Дифференцирование (4.76)

проведение тех же самых преобра-

зований, что

и в

предыдущем случае, позволяет получить формулу

для пересчета текущих коэффициентов регрессии следующего вида:

B(f)=B(/-l)

A'—§Ц^—^-^(/-1)]

х,С

_]Х,

+ а

М)

МВ-В(

-1))].

(

77)

X/C/.jX,

Полученная рекуррентная формула адаптивного механизма рег-

рессионной модели содержит два корректирующих слагаемых,

первое из которых является реакцией модели на ошибку прогно-

зирования,

второе — реакцией на несовпадение текущих коэф-

фициентов

коэффициентами модели экспертных ожиданий.

Адаптивная модель для этого случая имеет вид

=х,

В(0; (4-78)

В(/

= В(/)

ffi

\у

- х

Щ]

t+v^t

t+[ +

+ (l

Я'

) ffi+' [х

(В

В(0)];

(

165

С"

-i-1

C~V x Г"

(4.80)

Графическая иллюстрация результатов моделирования переход-

ного процесса, полученных с использованием выведенных здесь

рекуррентных соотношений, представлена на рис. 4.1.

0 5 10 15 20 25 30

—— Траектория переходного процесса —•— Траектория

А Траектория II

Рис.

4.1. Прогнозные траектории развития экономического процесса

На графике легко выделяются четыре участка: ретроспективный

и три прогнозных, характеризующих ожидаемые траектории раз-

вития экономического процесса. На первом из трех прогнозных

абсолютным доверием пользуется экстраполяция, на втором —

предпочтение отдается траектории, реализующей переходной про-

цесс,

и, наконец, на третьем участке абсолютное доверие смеща-

ется к экспертным оценкам.

Несмотря на то, что в основу построения моделей (4.72)—

(4.74) и (4.78)—(4.80) положены одни и те же идеи, применяются

они в разных ситуациях.

Первая модель, как правило, используется в тех случаях, когда

не удается получить формального представления о тенденциях эксперт-

ных ожиданий, а сами экспертные ожидания — не что иное, как

количественные оценки прогнозируемого показателя, которым экс-

перты отдали свое предпочтение при сравнении с другими.

Вторую модель рекомендуется использовать там, где, в прин-

ципе, количественные оценки могут даже отсутствовать, но у

экспертов есть представление в виде некоторой закономерности,

в соответствии с которой они формируют свои представления.

166

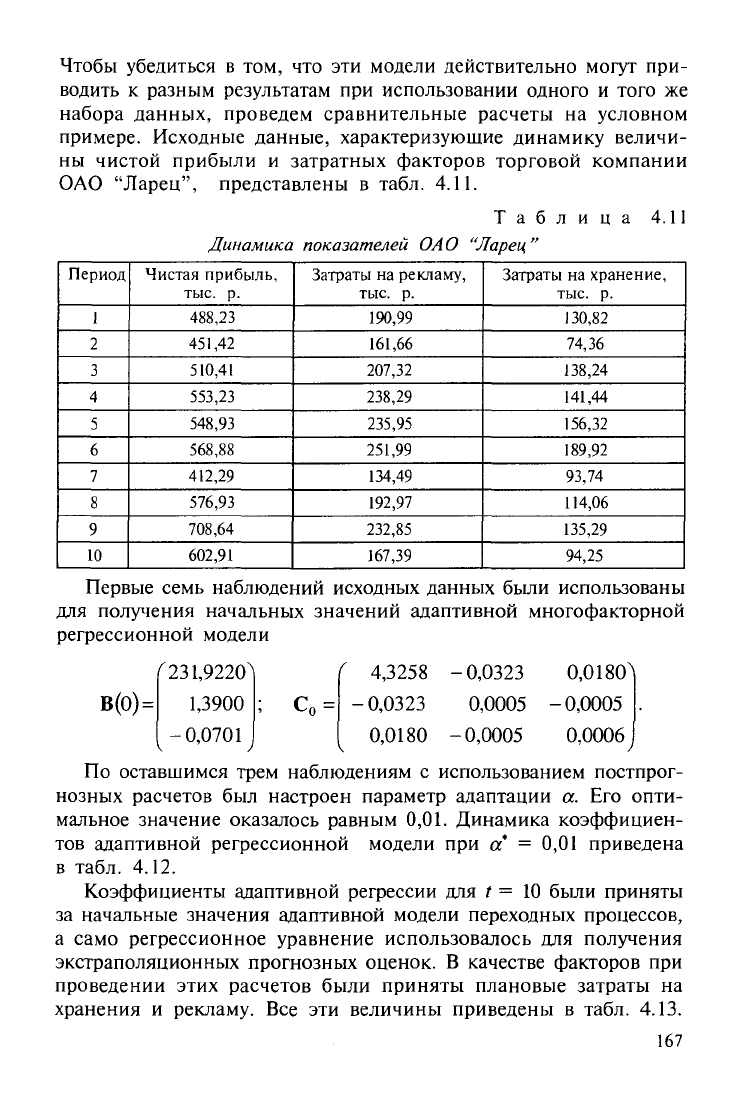
Чтобы убедиться в том, что эти модели действительно могут при-

водить к разным результатам при использовании одного и того же

набора данных, проведем сравнительные расчеты на условном

примере. Исходные данные, характеризующие динамику величи-

ны чистой прибыли и затратных факторов торговой компании

ОАО "Ларец", представлены в табл. 4.11.

Таблица

Динамика

показателей

ОАО "Ларец"

4.11

Период

Чистая прибыль,

тыс.

р.

488,23

451,42

510,41

553,23

548,93

568,88

412,29

576,93

708,64

602,91

Затраты на рекламу,

тыс.

р.

190,99

161,66

207,32

238,29

235,95

251,99

134,49

192,97

232,85

167,39

Затраты на хранение,

тыс.

р.

130,82

74,36

138,24

141,44

156,32

189,92

93,74

114,06

135,29

94,25

Первые семь наблюдений исходных данных были использованы

для получения начальных значений адаптивной многофакторной

регрессионной модели

в(о)=

^231,9220

1,3900

-0,0701

4,3258 -0,0323

•0,0323

0,0005

0,0180 -0,0005

0,0180^

-0,0005

0,0006

По оставшимся трем наблюдениям с использованием постпрог-

нозных расчетов был настроен параметр адаптации а. Его опти-

мальное значение оказалось равным 0,01. Динамика коэффициен-

тов адаптивной регрессионной модели при а = 0,01 приведена

в табл. 4.12.

Коэффициенты адаптивной регрессии для t = 10 были приняты

за начальные значения адаптивной модели переходных процессов,

а само регрессионное уравнение использовалось для получения

экстраполяционных прогнозных оценок. В качестве факторов при

проведении этих расчетов были приняты плановые затраты на

хранения и рекламу. Все эти величины приведены в табл. 4.13.

167

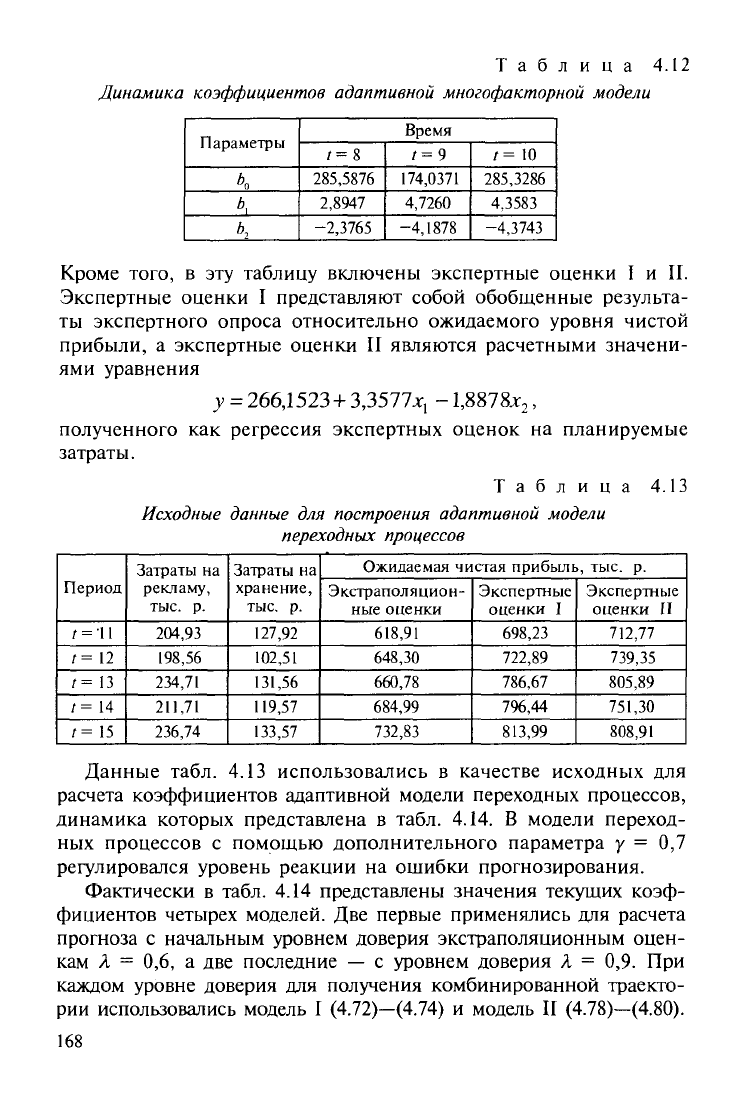
Таблица 4.12

Динамика коэффициентов адаптивной многофакторной модели

Параметры

*о

ъ,

Время

Г=8

285,5876

2,8947

-2,3765

1 =

174,0371

4,7260

-4,1878

/= 10

285,3286

4,3583

-4,3743

Кроме того, в эту таблицу включены экспертные оценки I и II.

Экспертные оценки I представляют собой обобщенные результа-

ты экспертного опроса относительно ожидаемого уровня чистой

прибыли, а экспертные оценки II являются расчетными значени-

ями уравнения

у = 266,1523 + 3,3577*, -1,8878*

полученного как регрессия экспертных оценок на планируемые

затраты.

Таблица 4.13

Исходные данные

для

построения адаптивной модели

переходных процессов

Период

t =11

/= 12

t= 13

/= 14

/= 15

Затраты на

рекламу,

тыс.

р.

204,93

198,56

234,71

211,71

236,74

Затраты на

хранение,

тыс.

р.

127,92

102,51

131,56

119,57

133,57

Ожидаемая чистая прибыль, тыс. р.

Экстраполяцион-

ные оценки

618,91

648,30

660,78

684,99

732,83

Экспертные

оценки I

698,23

722,89

786,67

796,44

813,99

Экспертные

оценки II

712,77

739,35

805,89

751,30

808,91

Данные табл. 4.13 использовались в качестве исходных для

расчета коэффициентов адаптивной модели переходных процессов,

динамика которых представлена в табл. 4.14. В модели переход-

ных процессов с помощью дополнительного параметра у = 0,7

регулировался уровень реакции на ошибки прогнозирования.

Фактически в табл. 4.14 представлены значения текущих коэф-

фициентов четырех моделей. Две первые применялись для расчета

прогноза с начальным уровнем доверия экстраполяционным оцен-

кам Я = 0,6, а две последние — с уровнем доверия Я = 0,9. При

каждом уровне доверия для получения комбинированной траекто-

рии использовались модель I (4.72)—(4.74) и модель II (4.78)—(4.80).

168

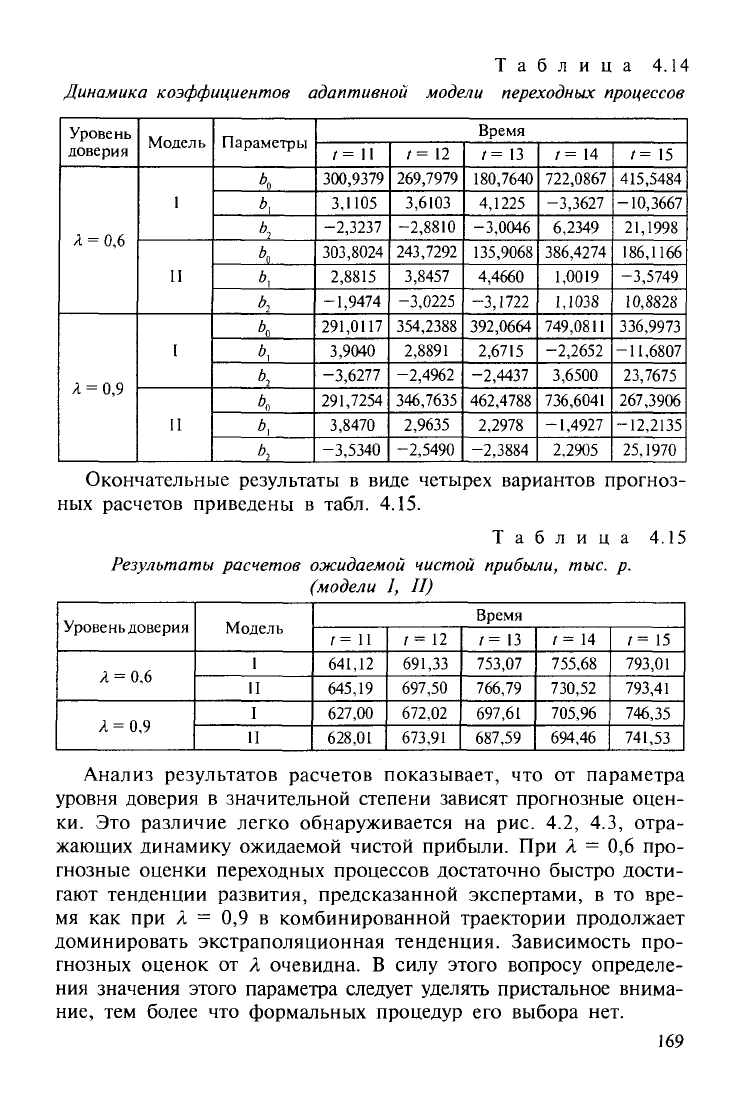
Таблица

4.14

Динамика коэффициентов

адаптивной модели

переходных процессов

Уровень

доверия

= 0,6

= 0,9

Модель

Параметры

*о

*•

Ьг

ь,

Время

300,9379

3,1105

-2,3237

303,8024

2,8815

-1,9474

291,0117

3,9040

-3,6277

291,7254

3,8470

-3,5340

269,7979

3,6103

-2,8810

243,7292

3,8457

-3,0225

354,2388

2,8891

-2,4962

346,7635

2,9635

-2,5490

180,7640

4,1225

-3,0046

135,9068

4,4660

-3,1722

392,0664

2,6715

-2,4437

462,4788

2,2978

-2,3884

722,0867

-3,3627

6,2349

386,4274

1,0019

1,1038

749,0811

-2,2652

3,6500

736,6041

-1,4927

2,2905

415,5484

-10,3667

21,1998

186,1166

-3,5749

10,8828

336,9973

-11,6807

23,7675

267,3906

-12,2135

25,1970

Окончательные результаты

виде четырех вариантов прогноз-

ных расчетов приведены

табл.

4.15.

Таблица

4.15

Результаты расчетов ожидаемой чистой

прибыли,

тыс.

р.

(модели

I, II)

Уровень доверия

= 0,6

= 0,9

Модель

Время

641,12

645,19

627,00

628,01

691,33

697,50

672,02

673,91

753,07

766,79

697,61

687,59

755,68

730,52

705,96

694,46

793,01

793,41

746,35

741,53

Анализ результатов расчетов показывает,

что от

параметра

уровня доверия

значительной степени зависят прогнозные оцен-

ки.

Это

различие легко обнаруживается

на рис. 4.2, 4.3,

отра-

жающих динамику ожидаемой чистой прибыли.

При А = 0,6

про-

гнозные оценки переходных процессов достаточно быстро дости-

гают тенденции развития, предсказанной экспертами,

в то

вре-

мя

как при А = 0,9 в

комбинированной траектории продолжает

доминировать экстраполяционная тенденция. Зависимость про-

гнозных оценок

от А

очевидна.

силу этого вопросу определе-

ния значения этого параметра следует уделять пристальное внима-

ние,

тем

более

что

формальных процедур

его

выбора

нет.

169