Das Sh.P. Statistical Physics of Liquids at Freezing and Beyond

Подождите немного. Документ загружается.

1.3 Time correlation functions 41

1.3.2 The self-correlation function

The dynamics of a single particle moving in a surrounding ﬂuid can be described in terms

of the density of the single particle ˆn

(r, t) deﬁned as the tagged particle (α) density,

ˆn

(r, t) = δ(r − r

(t)). (1.3.27)

The average ˆn

 of the tagged particle density is obtained as

n

(r, t)=

(1.3.28)

and goes to zero in the thermodynamic limit V →∞. The correlation of the tagged-

particle density at two different times deﬁnes the van Hove correlation function,

(|r − r



|, t) = V δ ˆn

(r, t)δ ˆn



, 0)

= V δ(r − r

(t))δ(r



− r

(0))−V

−1

. (1.3.29)

The tagged-particle density ˆn

(r, t) is δ(r − r

(t)), with r

(t) denoting the position of the

tagged particle at time t. In an isotropic ﬂuid G

(r, t) is a function of r only. The Fourier

transform of G

is the self-part of the density correlation function deﬁned above in eqn.

(1.3.23).Fromeqn. (1.3.29) G

(r, t) can be interpreted as the probability per unit volume

of ﬁnding a particle at a distance r at a given time t, given that it was at the origin r = 0at

t = 0. Note that, using eqn. (1.3.28), it follows from the deﬁnition of G

(r, t) that

(r, 0) = δ(r) and



dr G

(r, t) = 1. (1.3.30)

Equation (1.3.30) is a statement of the conservation of probability. In an isotropic ﬂuid G

is a function of r only and 4πr

(r, t) represents the probability of ﬁnding a particle at

r at time t given that it was at the origin at time t = 0. In Fig. 1.7 we show schematically

how this probability distribution spreads out with the passage of time.

The frequency transform S

(k,ω)of G

is deﬁned, with

(k, t) =



+∞

−∞

dr e

ik · r

(r, t), (1.3.31)

(k,ω) =



+∞

−∞

dt e

iωt

(k, t). (1.3.32)

The tagged-particle correlation is obtained directly from the measurement of S

(k,ω) in

neutron-scattering experiments (Fig. 1.8). The coherent component of the scattered inten-

sity is proportional to the self part of the correlation function and from it one directly

obtains the information on the single-particle dynamics.

42 Statistical physics of liquids

Fig. 1.7 A schematic representation of how G

(r, t) spreads out with time.

Fig. 1.8 Dependence of the correlation function

S(Q, E) for coherent (solid) and incoherent

(dashed) neutron-scattering analysis of argon at the frequency E (in meV) and the wave-number

Q (in the Å

−1

) plane. From Sköld et al. (1972).

 American Physical Society.

The free-particle limit

It is straightforward to demonstrate that the function G

(r, t) and hence its Fourier trans-

form F

(k, t) have a Gaussian distribution in the t → 0 limit. In the very-short-time regime,

the particle moves as a free one, and G

(r, t) varies spatially as a narrow Gaussian distri-

bution function. In the free-particle limit it is straightforward to use the above deﬁnition in

1.3 Time correlation functions 43

terms of probability to compute

(r, t) =



dp φ

( p)δ



r −





2πv



3/2

exp



−







, (1.3.33)

where φ

is the Maxwellian momentum distribution. For the free particle motion the par-

ticle with momentum p moves a distance r = pt/m. The corresponding Fourier transform

(k, t) and the frequency transform S

(k,ω) are obtained as the following Gaussian

functions:

(k, t) = exp



−

(kv



(k,ω) =

√

2π

exp



−







. (1.3.34)

The behavior predicted by (1.3.34) is seen in Fig. 1.8. Therefore in the short-time or free-

particle limit the correlation functions remain Gaussian.

The time correlation of the velocities of a tagged particle at two different times plays an

important role in the description of the single-particle dynamics in a ﬂuid. This is deﬁned

in three dimensions as

(t) =

v(t) · v(0). (1.3.35)

For short times once again we can expand v(t) at t = 0 and compute the above correlation

function. The ﬁrst-order term goes to zero on using eqn. (1.3.7), and the leading-order

contribution reads

(t) = v



1 −



+···



, (1.3.36)

where v

= k

T /m is the thermal velocity of a particle,

v(0) · v(0). (1.3.37)

The quantity 

has the dimension of frequency and is obtained as



3mk

{m

v}· {m

v} =

3mk

F · F, (1.3.38)

where F is the force exerted on the particle α by its neighbors. For a system in which the

interactions between the particles are described by the pairwise additive potential v(12),

we show in Appendix A1.2 by evaluating the force–force correlation function that 

can

be expressed in terms of the pair correlation function g(r) by the following relation:





∇

v(r)g(r)dr. (1.3.39)

44 Statistical physics of liquids



is termed the Einstein frequency, since for short times it represents the frequency of

vibration of the tagged particle undergoing small oscillations in the potential well pro-

duced by its neighbors. Note that the above analysis holds only for continuous potentials.

For hard-sphere systems such an analysis does not hold. In this case the linear-order term

contributes, and it has been shown (Lebowitz et al., 1969) that the autocorrelation function

has the exponentially decaying form

(t) = v

[

1 − 

t +···

]

≈ e

−

, (1.3.40)

where the frequency 

= 2/(3t

), with t

being the Boltzmann collision time, given by

−1

4πn

√

βmπ

. (1.3.41)

For higher densities the structure of t

is replaced by the corresponding Enskog time t

/g(σ ). The decay of the tagged-particle correlation for a dense hard-sphere system is

therefore exponential and is given by

(t) = v

exp



−



. (1.3.42)

The exponential decay of ϕ

(t) is a result of the completely random nature of uncorrelated

binary collisions of the particles. Cooperative effects coming from longer length scales

cause nonexponential or power-law decays in the correlation functions. We discuss such

contributions to correlation functions in subsequent chapters.

Long-time dynamics

From the general deﬁnition (1.3.23) of the tagged-particle correlation (since all the particles

are identical) we obtain

(k, t) =

ik · (r

(t)−r

(0))

ikd(t)

, (1.3.43)

where d(t) =

k · (r

(t) − r

(0)), with

k being the unit vector in the direction of the wave

vector. The terms with odd powers of k vanish in the above expansion, meaning that the

equilibrium correlation function F

(k, t) for the isotropic ﬂuid is a function of |k| only,

(k, t) = 1 −

d

(t)+

d

(t)+···. (1.3.44)

In order to organize the Gaussian and non-Gaussian parts of F

(k, t), we write the above

expansion in terms of time-dependent functions 

(t),forn = 1, 2,... (Rahman et al.,

1962),

(k, t) = exp



−k



(t) + k



(t) − k



(t) +···

. (1.3.45)

1.3 Time correlation functions 45

On comparing coefﬁcients of the different powers of k in eqns. (1.3.44) and (1.3.45),we

obtain for the different 

(t)



(t) =

d

(t), (1.3.46)



(t) =



d

(t)−3d

(t)

, (1.3.47)



(t) =



d

(t)−15d

(t)d

(t)+30d

(t)

. (1.3.48)

The Gaussian part of F

(k, t) is determined by 

(t), while the 

for n ≥ 2 represent

the non-Gaussian part. We demonstrate in the following that the function 

(t) can be

expressed in terms of the two-point current correlation function ϕ

(t).

In order to see the link between the tagged-particle correlations and the velocity corre-

lations, we express the displacement of the tagged particle as an integral over its velocity.

Thus, if we denote by u(t) the component of the velocity v of the tagged particle α in the

direction of k, d(t) is obtained in terms of u as

d(t) =

k · (r

(t) − r

(0)) =



tu(t ). (1.3.49)

Since F

(k, t) =exp(ikd(t)), we obtain the exponential on the RHS as a formal solution

of the equation

∂

∂t

ikd(t)

= iku(t)e

ikd(t)

(1.3.50)

in the following form by iteration:

ikd(t)

= 1 + ik





u(t



ikd(t



)

= 1 + ik



u(t

) + (ik)



u(t

)



u(t

) +···. (1.3.51)

On taking an average of the above equation, since in the isotropic ﬂuid in equilibrium on

average odd powers of u vanish, we obtain the tagged-particle correlation in terms of the

expansion

(k, t) =

∞



n=0

(−k

)



...



u(t

)u(t

)...u(t

). (1.3.52)

Now straightforward comparison of powers of k

with the deﬁnition (1.3.45) shows that



(t) =



u(t

)u(t

), (1.3.53)



(t) =



u(t

)u(t

)−



(t), (1.3.54)

46 Statistical physics of liquids

and so on. Using the property of time translational invariance of the equilibrium correlation

functions of u, the integral expression for 

(t) is expressed in terms of the two-point

velocity correlation functions ϕ

− t

) as follows:



(t) =



u(t

)u(t

)=



ds ϕ

(s)



ds ϕ

(s) −



ds ϕ

(s)

= t



ds ϕ

(s) −



sϕ

(s)ds, (1.3.55)

where in reaching the ﬁnal result we integrated the second term on the RHS by parts. There-

fore, if the non-Gaussian effects are ignored, the tagged-particle correlation is entirely

determined by ϕ

(t). For an isotropic liquid d

(t)=

r

(t) in three dimensions, giving

the result

r

(t)=6t



(s)ds, (1.3.56)

where we have ignored the contribution from the second term on the RHS of eqn. (1.3.55).

The latter is a constant when the velocity correlation function decays in an exponential

manner. However, it has been observed from the computer molecular-dynamic simulations

(Alder and Wainwright, 1967, 1970) of ﬂuids that the velocity autocorrelation ϕ

(t) has a

long-time tail decaying as t

−3/2

in three dimensions. This long-time tail in ϕ

(s) makes the

second integral grow as t

1/2

. This makes the long-time (t →∞), long-distance (k → 0)

behavior of F

(k, t) very different from the simple exponential prediction. However, the

long-time decay of the tagged-particle correlation is still well behaved since we consider

the limit k → 0 and t →∞such that k

t remains ﬁnite. The factor k



(t) on the RHS

of eqn. (1.3.45) is ﬁnite in this limit. Therefore, for a system in which the dynamics is

Gaussian, all the 

(t) for n ≥ 2 in the exponent on the RHS of (1.3.45) vanish and the

tagged-particle correlation is obtained in the form

(k, t) = exp



−k

t

(t)

= exp



−k



(s)ds



. (1.3.57)

Hence in the Gaussian limit F

(k, t) is determined in terms of the velocity correlation

function ϕ

(t) only.

Non-Gaussian effects The non-Gaussian effect in the single-particle dynamics is related to

higher (than-two-point) correlation functions in the ﬂuid and was ﬁrst studied for molecular-

dynamics simulations (Rahman, 1964) of argon. The expansion (1.3.45) is reorganized in

terms of parameters α

(t) for n = 1, 2, 3,... for the isotropic system as (Nijboer and

Rahman, 1966)

(k, t) = e

−

(t)



1 +



(t)

(t) −



(t)

{α

(t) − 3α

(t)}...



, (1.3.58)

1.3 Time correlation functions 47

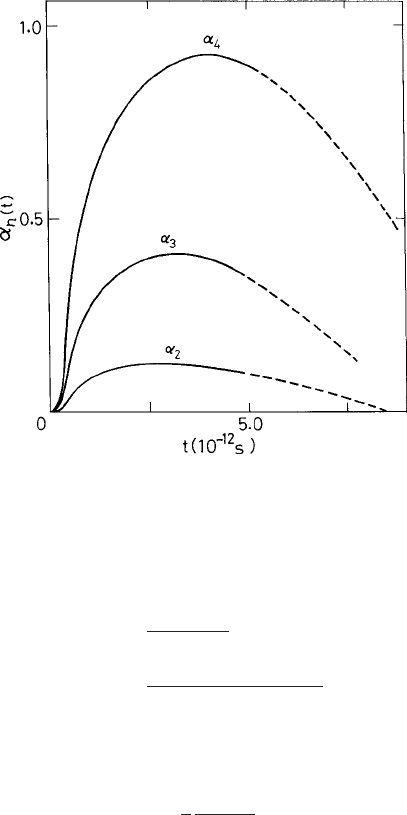
Fig. 1.9 Non-Gaussian parameters α

(t) for n = 2, 3, and 4 vs. time t (in units of 10

−12

s) obtained

from results of molecular-dynamic simulations of argon. From Rahman (1964).

where we have deﬁned 

(t) = k



(t).Theα

are obtained as

(t) =

r

(t)

r

(t)

− 1, (1.3.59)

1 ·3 ·5 ·····(2n +1)

. (1.3.60)

In particular, the above deﬁnition gives α

(t) = 1 and the ﬁrst non-Gaussian parameter

(t) as

(t) =

(t)

− 1. (1.3.61)

In Fig. 1.9 the so-called non-Gaussian parameters α

(t) for n = 2, 3, and 4 are shown,

with all quantities peaking at an intermediate time. The non-Gaussian parts are computed

from molecular-dynamic simulation of argon (Rahman, 1964).

1.3.3 The linear response function

An important application of the equilibrium correlation functions lies in the formula-

tion of a linear response to an external perturbation. Let us consider the case in which

48 Statistical physics of liquids

a time-dependent external ﬁeld h

(r, t) couples to the dynamic variable ˆa(r). The Hamil-

tonian of the system in the presence of the external ﬁeld is obtained as a sum of two parts,

H = H

+ H



(t), (1.3.62)

where H

is the unperturbed system and H



is the perturbation,



(t) =−



ˆa(r)h

(r, t)dr. (1.3.63)

The ﬂuctuation in the average value of a dynamic variable

b(x) is obtained by taking a

phase-space average with respect to the distribution function f

(N )

(t).

The time evolution of the phase-space probability density f

(N )

(t) for the perturbed den-

sity is determined from the Liouville equation (1.1.22). In order to keep the notation simple,

we drop the dependence of f

(N )

on the phase-space variables. We deﬁne the ﬂuctuation

from the equilibrium  f

(N )

(t) = f

(N )

+  f

(N )

(t), (1.3.64)

where f

(N )

is the equilibrium distribution which satisﬁes

∂ f

(N )

∂t

=−i L

(N )

, f

(N )

= 0. (1.3.65)

The symbol {}here denotes the Poisson brackets between the corresponding dynamic

variables and L

is the Liouville operator with the unperturbed Hamiltonian H

.Fromthe

Liouville equation the time evolution of f

(N )

is obtained as

∂f

(N )

∂t

=−i L f

(N )

={H, f

(N )

}

={H

, f

(N )

}+{H



, f

(N )

}

=−i L

 f

(N )

−





ˆa(r



), f

(N )



, t). (1.3.66)

The solution of the above equation with the boundary condition f

(N )

(−∞) = f

(N )

 f

(N )

(t) =−



−∞









−i(t −t



ˆa(r



), f

(N )



, t



). (1.3.67)

The ﬂuctuation in a dynamic variable

b(r) at time t is obtained from the corresponding

phase-space average with  f

(N )

(, t) by integrating over all the 6N phase-space variables,

collectively denoted as ,



b(r, t)=



d

b(r) f

(N )

(, t)

=−



−∞









d



−i(t −t



ˆa(r



), f

(N )

b(r)h



, t



)

≡



+∞

−∞





(r − r



, t − t



, t



), (1.3.68)

1.3 Time correlation functions 49

where R

(r − r



, t − t



) is the linear response function in the liquid with time and spatial

translational invariance. From the above expression the response function is obtained as

(r − r



, t − t



) =−(t − t



)



d

ˆa(r



, t



), f

(N )

b(r, t), (1.3.69)

where (t) is the Heaviside step function, which is equal to 1 and 0 for x < 0 and x > 0,

respectively.

An important result of equilibrium statistical mechanics is a relation between the linear-

response function and correlation functions that is termed the ﬂuctuation–dissipation the-

orem (FDT). It follows directly then, using the deﬁnition of Poisson brackets, that the

response function can be expressed in a more symmetric form in terms of the equilibrium

average of the Poisson bracket,

(r − r



, t − t



) =−(t − t



){

b(r, t), ˆa(r



, t



)}

, (1.3.70)

where the subscript 0 on the angular bracket implies averaging with respect to the unper-

turbed Hamiltonian H

. Using the canonical distribution function f

(N )

∼ exp(−β H

),it

can be shown directly from (1.3.69) that

ˆa(r



, t



), f

(N )

=−β f

(N )

∂ ˆa(r



, t



)

∂t



. (1.3.71)

Using the above result in eqn. (1.3.69) gives the following relation between the correlation

function and the corresponding response function:

(t − t



) = (t − t



)

∂C

∂t

, (1.3.72)

where C

is the correlation function averaged over the equilibrium distribution. In equi-

librium we assume that time translational invariance holds for the correlation function,

i.e., C

(t, t



) ≡ C

(t − t



). The relation (1.3.72) is the ﬂuctuation–dissipation theorem

(FDT). We have dropped the dependence on spatial coordinates in eqn. (1.3.72) for the sake

of simplicity. The Laplace transform (Abramowitz and Stegun, 1965)oftheR(z) response

function is deﬁned as

(z) =−i



∞

dt e

izt

(t), Im(z)>0. (1.3.73)

Since ˆa and

b are both real functions, it follows directly that for the real and imaginary parts

of the response function R(z), denoted by R



and R



, respectively, one has the following

symmetry properties:



(ω) = R



(−ω), (1.3.74)



(ω) =−R



(−ω). (1.3.75)

Equations (1.3.72)–(1.3.74) hold both for real space and for the corresponding Fourier-

transformed quantities, and it is not explicitly mentioned which for simplicity.

50 Statistical physics of liquids

1.4 Brownian motion

In the earlier sections our discussion of the dynamic correlation functions involved deal-

ing with the phase-space variables in the 6N -dimensional space at the microscopic level.

The kinetic theory of many-particle systems evolving under Liouville dynamics provides

the basic tool for calculating the correlation functions in this case. Computer molecular-

dynamics simulations dealing with the microscopic coordinates of a small number of

particles also constitute another useful tool for theoretically obtaining the correlation func-

tions. An alternative approach to these methods is to study the dynamics in terms of a

chosen set of dynamic variables. The basic criterion involved in this method is separat-

ing the dynamics into a slow part and a fast part. The choice of the set of variables is

motivated in order to exploit the widely varying time scales in the dynamics. The cor-

relations of the slow modes are then computed by treating the rest of the degrees of

freedom as noise, this noise being completely random on the time scale of the slow modes.

A classic example of the treatment of dynamics with stochastic noise is the Brownian

motion which we will introduce in the following. The theory of Brownian motion discussed

here was developed by Einstein (1905), Smoluchowski (1906), Planck (1917), and others

(Chandrasekhar, 1943). It constitutes an approach to the dynamics of a many-particle

system that is an alternative to the Liouvillian or Newtonian dynamics. In formulating

the dynamics of a ﬂuid we will largely follow a generalization of such a scheme in the

subsequent chapters of this book.

1.4.1 The Langevin equation

Small grains of pollen immersed in a ﬂuid undergo a kind of perpetual irregular motion.

This is termed Brownian motion after the name of the botanist Robert Brown, who ﬁrst

observed this phenomenon in 1827. The irregular motion is due to the incessant random

collisions of the molecules of the surrounding ﬂuid with the pollen grain or the so-called

Brownian particle. The mass of this particle is much higher than that of a colliding particle

of the surrounding ﬂuid. The equation of motion of the Brownian particle is obtained in

terms of a Langevin equation involving a stochastic part distinct from the completely deter-

ministic Newtonian dynamics. This formulation of the problem is based on the assumption

that the motion of the Brownian particle is controlled by forces varying on very different

time scales and hence the equation of motion consists of a slow part and a fast part. The

latter is termed noise, and calculation of the correlations of dynamic variables now implies

treating different realizations of the noise.

The equation of motion of a heavy Brownian particle of mass m moving in a sea of

particles is written in the following form:

=−ζv

(t) + f

(t), (1.4.1)