Das Sh.P. Statistical Physics of Liquids at Freezing and Beyond

Подождите немного. Документ загружается.

1.2 Equilibrium properties 31

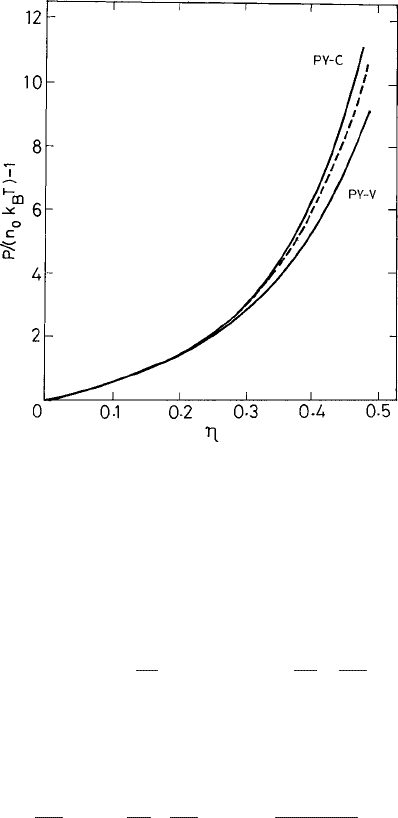
Fig. 1.4 The equation of state giving P/(nk

T ) − 1 vs. the packing fraction η for hard spheres

according to the Percus–Yevick theory using the compressibility (PY-C) (eqn. (1.2.103)) and virial

(PY-V) (eqn. (1.2.106)) routes. The result from the Carnahan–Starling equation is shown as a dashed

line.

used. The Helmholtz free energy of the liquid is obtained by integrating the thermodynamic

relation P =−(∂ F/∂ V )

F =−



PdV = N



P = Nk



d ¯ϕ

¯ϕ



β P



. (1.2.114)

The corresponding expression for the excess free energy of the hard-sphere liquid (in

addition to the ideal-gas or noninteracting part) given in eqn. (1.2.114) is obtained by

integrating the Carnahan–Starling equation of state,

β F



d ¯ϕ

¯ϕ



β P

− 1



ϕ(4 −3ϕ)

(1 − ϕ)

. (1.2.115)

On the other hand, on using either the PY or the HNC closure we will obtain two equa-

tions of state for the virial and compressibility conditions. This problem was addressed

by proposing bridge functions to interpolate between the two schemes given in (1.2.91)

and (1.2.92). The bridge function is adjusted to achieve full consistency between the two

equations of state (Rogers and Young, 1984).

Long-range interaction

For interaction potentials that have a long-range attractive part in addition to the short-

range repulsive part, the closure schemes described above are not very useful. In this case

the two-body interaction potential u(r) is divided into a harshly repulsive short-range u

(r)

32 Statistical physics of liquids

part and a weak attractive part u

(r) effective over long distances. In the conventional

mean-spherical approximation (MSA) (Lebowitz and Penrose, 1966) this situation was

initially treated by taking u

as a hard-sphere potential so that the resulting integral equa-

tion reduces to the PY equation with u

= 0. This approach was subsequently generalized

to schemes in which u

is continuous though strongly repulsive (Chihara, 1973; Madden

and Rice, 1980). This is referred to as “soft-core” MSA (SMSA). We consider here the

scheme developed by Weeks, Chandler, and Andersen for systems with long-range attrac-

tive potentials (Chandler and Weeks, 1970; Weeks et al., 1971; Andersen et al., 1971).

In the WCA theory the two-body interaction potential u(r) is divided into a short-range

repulsive part u

(r) and a long-range attractive part u

(r),

u(r) = u

(r) + u

(r). (1.2.116)

A typical example is the spherically symmetric Lennard-Jones (LJ) interaction potential,

for which such a division (Weeks et al., 1971) is made as follows. The LJ interaction

potential u(r) ≡ u

(r) for two particles at a distance r is deﬁned as

(r) = 4







−







≡ w(r), (1.2.117)

where 

is the depth of the potential at its minimum and σ is the scale associated with

the potential. u

is written as a sum of two parts, a hard-core repulsive part u

and an

attractive part u

, respectively deﬁned as

≡ u

(r) =

w(r ) + 

, for r <σ

0, for r >σ

(1.2.118)

and

≡ u

(r) =

−

, for r <σ

w(r ), for r >σ

(1.2.119)

where σ

= 2

1/6

σ . For the homogeneous liquid state, its thermodynamic properties are

obtained by treating the weak attraction u

as a perturbation of a reference system having

an interaction potential u

The thermodynamic property of the system with the given interaction potential u(r)

is obtained as a sum of two contributions: ﬁrst, that of a reference system having the

purely repulsive interaction u

(12); and second, the contribution due to the attractive part

of the interaction u

(12), which is obtained by treating the latter as a weak perturbation. In

the ﬁrst part, the properties of the reference system are usually known from independent

models. The most commonly used reference system is the one with hard-sphere potential

interaction potential u

(r), with diameter d characterizing the hard-sphere potential (for

its deﬁnition see eqn. (1.2.93)). This choice of the hard-sphere system is motivated by the

fact that there exist several models that accurately describe its thermodynamic properties

1.2 Equilibrium properties 33

for densities ranging from low to very high values. Some of these have already been dis-

cussed above. The diameter of the reference hard-sphere liquid system is chosen such that

the corresponding thermodynamic free energy is equal to that of the original system with

interaction potential u

(12). The dependence of the free energy F on the interaction poten-

tial u

(r) is treated in terms of the function e

(r) = exp(−βu

(r)), which changes sharply

at the effective range of the harshly repulsive potential u

(r). The corresponding quantity

for the hard-sphere potential e

(r) = exp(−βu

(r)), on the other hand, changes discon-

tinuously from 0 to 1 at r = d. The difference between the “e” functions corresponding to

the reference and the hard-sphere systems deﬁnes the function

e

(r) = e

(r) − e

(r). (1.2.120)

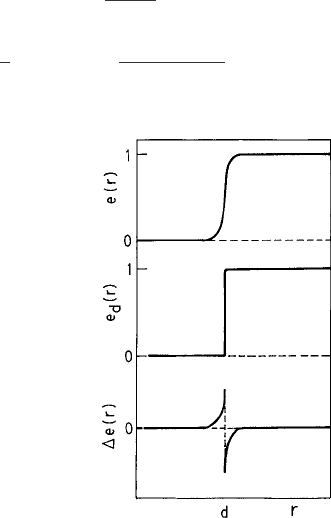
The “blip function” e

(r) is nonzero only in a small range of O(d) (say) around r = d

which is the diameter of the equivalent hard-sphere system. This is shown schematically in

Fig. 1.5. Since the blip function is identically zero if u

(r) = u

(r), the free energy of the

reference system is expressed in a functional Taylor expansion in powers of e

(r) around

the free energy of the equivalent hard-sphere system (EHS):

F[u

]=F[u



δF

δe

(r)

e

(r)





δe

(r)δe



)

e

(r)e



) +···. (1.2.121)

Fig. 1.5 The Boltzmann factors e

(r) for the potential u

(r); e

(r) for the hard-sphere potential

(r); and the blip function e

(r) vs. r.

34 Statistical physics of liquids

We note ﬁrst that the functional derivative in the second term on the RHS above is evalu-

ated, noting that F =−k

T ln Z

,as

δF

δe

(r)





δF

δu



)

δu



)

δe

(r)

= k







−

δZ

δu



)



δu



)

δe

(r)

. (1.2.122)

Since −βu

(r) = ln e

(r) the functional derivative

− β

δu



)

δe

(r)

= e

βu

(r)

δ(r − r



). (1.2.123)

If the potential-energy part U of the Hamiltonian involves only two-body interactions as

in the deﬁnition (1.2.63), the integral

I (say) in the square bracket on the RHS of eqn.

(1.2.122) is further simpliﬁed. In this case the derivative of U with respect to the two-body

potential u

(r) is simply a sum of delta functions,

I =

N !Z



...



−βU(r

,...,r

)



δU

δu



)





i, j=1



−βU(r

,..., r

)

N !Z



δ(r



− r

)dr

...dr

. (1.2.124)

For a system of identical particles all the different N(N − 1) choices for the pairs in

the sum above give the same integral. For the translationally invariant system the integral

≡ Vdr

,giving

I =

N !

(N − 2)!



δ(r



− r

)



−βU(r

,...,r

)

N !Z



... dr

βV

N !

(N − 2)!



−βU(r



; r

,...,r

)

N !Z



... dr

= β

g(r



). (1.2.125)

Hence, using eqns. (1.2.123) and (1.2.125) in eqn. (1.2.122), we obtain the result

δF

δe

(r)

=−k





g(r



)

βu



)

δ(r − r



)

=−

Nnk

Ty(r). (1.2.126)

Using this relation, the expansion (1.2.122) for the free energy is obtained as

F[u

]=F[u

]−Nk



dr y

(r)e

(r) +···. (1.2.127)

The free energy of the reference system is made equal to that of the equivalent hard-sphere

system by setting the ﬁrst-order term in the RHS of eqn. (1.2.121) equal to zero. Thus the

1.2 Equilibrium properties 35

diameter d is determined from the condition



dr y

(r)e

(r) = 0. (1.2.128)

The diameter d is obtained by numerically solving the above equation using the hard-

sphere pair correlation functions and the y function.

Since the function e

(r) is nonzero only in a small region around r = d, the above

condition is evaluated to leading order by replacing y

with its value at this point. The

integral on the LHS of eqn. (1.2.128) is then obtained (using the deﬁnition (1.2.120))as



dr{e

(r) − e

(r)}=



∞

dr e

−βu

(r)

−



∞

dr. (1.2.129)

We have used the fact that e

(r) equals 0 for r < d and 1 for r > d.Fromeqn. (1.2.129)

one obtains for d the result (Barker and Henderson, 1967)

d =



∞

(

1 − e

−βu

(r)

)

. (1.2.130)

In fact, with the condition (1.2.128) satisﬁed, the free energy of the reference system is

obtained in terms of that of the equivalent hard-sphere system (Chandler and Weeks, 1970;

Weeks et al., 1971, Andersen et al., 1971; Barker and Henderson, 1971)

F[u

]=F[u

]+O(

), (1.2.131)

where  is the range around r = d over which the blip function is nonzero. Note that the

value of d obtained from the solution of eqn. (1.2.128) depends both on the density n and on

the temperature T , whereas the d obtained from the Barker–Henderson relation (1.2.130)

depends only on the temperature. From eqns. (1.2.126) and (1.2.127) we obtain that to

leading orders y(r) = y

(r), and hence the pair correlation function for the reference

system is obtained as

(r) = e

−βu

(r)

(r) + O(

). (1.2.132)

The pair correlation function g(r) for the Lennard-Jones system is obtained in terms of

that of the equivalent hard-sphere system of diameter d from eqn. (1.2.132).

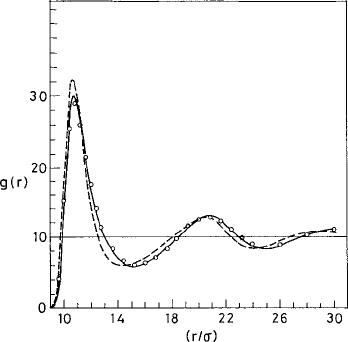
This is shown in Fig. 1.6. The corresponding g(r) obtained from molecular-dynamics

simulations as well as numerical solution of the Percus–Yevick equations for the Lennard-

Jones potential is also shown for comparison.

In Section 2.4.1 we will discuss the application of the WCA approach to obtain the

thermodynamic properties of the inhomogeneous solid state for a Lennard-Jones system.

The contribution to the free energy from the attractive part of the potential is added as a

mean-ﬁeld term (see eqn. (2.4.9) in Chapter 2) in this theory. Further improvements for

the thermodynamic properties (of the liquid) at higher densities are obtained by using the

bridge functions mentioned above to interpolate between the SMSA and the HNC equa-

tions (Zerah and Hansen, 1986; Due and Haymet, 1995; Due and Henderson, 1996). These

methods lead to values of the static structure factor for the liquid that are in agreement with

simulations at high densities.

36 Statistical physics of liquids

Fig. 1.6 The radial distribution function g(r) for the Lennard-Jones liquid at ρ

∗

= 0.85 and

∗

= 0.88. MD simulations by Verlet (1968) (open circles); the Percus–Yevick solution for the

pair function for the Lennard-Jones potential by Mandel et al. (1970) (dashed line); and the theory

of Weeks et al. (1971) described in the text (solid line).

 American Institute of Physics.

1.3 Time correlation functions

The time correlation of the microscopic densities, averaged over the equilibrium ensem-

ble, is an important ingredient in the study of the dynamics of a ﬂuid. Essentially all

experiments probing the dynamic properties of the ﬂuid are also analyzed in terms of

time correlation functions. Let

be a dynamic variable dependent on the phase-space

coordinates, denoted with the symbol {r

(t), p

(t)}≡

(t), deﬁned as

(t) = ψ

[

(t)]. (1.3.1)

For clarity we drop any possible spatial dependence of

. The hat on the variable is used

to denote that it is dependent on the phase-space variables. The time correlation function

is deﬁned as the correlation function of the ﬂuctuation of ψ

(t) and ψ



) (t > t



) around

the corresponding equilibrium average,

(t, t



) =δ

(t)δ



), (1.3.2)

where the angular brackets denote the average in the equilibrium ensemble in the following

way:

δ

(t)δ



)=



d



)δ

(t)δ



) f

[



)]



d



)exp[iL(t − t



)]δ



)δ



) f

[



)]. (1.3.3)

The equilibrium distribution f

is independent of time and hence C

is dependent only

on the difference of the two times C

(t, t



) = C

(t − t



). Of particular interest for the

1.3 Time correlation functions 37

discussion of the dynamics of liquids is the equilibrium averaged autocorrelation function,

which is deﬁned as

(t) =

(t)δ

∗

(0)

. (1.3.4)

Since C

(t) = C

(−t) it follows from the above deﬁnition that C

(t) is real for all

times. Using Schwarz’s inequality (Dennery and Krzwicki, 1967) for the autocorrelation

function,

(t)|≤

∗

= C

(0), (1.3.5)

i.e., the magnitude of the function is bound by its initial value. Indeed, in the long-time

limit, t →∞, the dynamic variables become uncorrelated and we have

lim

(t−t



)→∞

(t − t



)|=δ

(t)δ



)=0. (1.3.6)

An important property of the autocorrelation function is that its time derivative at t = 0

vanishes. In order to prove this, we note that, since ψ

(t + s)ψ

(s) is independent of s,

ψ

(t + s)ψ

(s)=0,



(t + s)ψ

(s)+ψ

(t + s)

(s)=0,

where the dot implies a derivative with respect to s. On setting s = 0 we obtain the result



(t)ψ

(0)=−ψ

(t)

(0). (1.3.7)

For the autocorrelation at t = 0wehavetheresult

ψ

(t)ψ

(0)

t=0

(0) = 0. (1.3.8)

For our discussions in this book it will be particularly useful to deﬁne the two-sided

Fourier transform

(ω) =



+∞

−∞

(t)e

iωt

dt (1.3.9)

and the one-sided Laplace transform

(z) =−i



+∞

(t)e

izt

dt, Im(z)>0. (1.3.10)

The two transforms are related in the following way:

(z) =−i



+∞

(t)e

izt



+∞

−∞

d ¯ω

2π



−i



+∞

dt e

i(z−¯ω)t



( ¯ω)



+∞

−∞

d ¯ω

2π



( ¯ω)

z −¯ω



38 Statistical physics of liquids

The above relation is further analyzed for the autocorrelation function using the standard

identity

lim

→0

ω ±i −¯ω

= P



ω −¯ω



∓i πδ(ω −¯ω), (1.3.11)

where P indicates the principal value. In this case, i.e., a ≡ b and the Fourier transform

(ω) is real, we obtain the following useful relations between the Fourier and Laplace

transforms of the correlation function:

(ω) =−2C



(ω +i), (1.3.12)



(ω +i) =−



d ¯ω





( ¯ω +i )

ω −¯ω



, (1.3.13)

for  → 0.

1.3.1 The density correlation function

For the ﬂuid generally we deﬁne for a microscopic variable

(r, t), corresponding to the

microscopic property a

(t) for the αth particle at position r

(t),

(r, t) =



α=1

δ(r − r

(t)). (1.3.14)

In Table 1.2 we list examples of a few types of experiments with the corresponding

dynamic variable a

whose time correlation is measured using the respective method. Our

discussion here will primarily involve the microscopic variables of mass density and

momentum density, deﬁned, respectively, as

ˆρ(r, t) =



mδ(r − r

(t)), (1.3.15)

g(r, t) =



δ(r − r

(t)). (1.3.16)

We put a hat on the slow variable to indicate the dependence on the phase-space coordi-

nates of this variable. Note that the mass density ˆρ(r, t) is similar to the single-particle

number density ˆn(r, t). For the one-component system in fact we have ˆρ = m ˆn.Weshow

in Appendix A5.1 that the mass and momentum densities are related by the continuity

equation

∂ ˆρ

∂t

+∇·

g = 0. (1.3.17)

The most important correlation function for our purpose is that of the density ﬂuctuations,

denoted by

δ ˆρ(r, t) =ˆρ(r, t) −ρ

, (1.3.18)

1.3 Time correlation functions 39

Table 1.2 Examples of correlation functions of a few dynamic variables and the

corresponding experiments which measure them.  implies a sum over the particle

index α = 1,...,N while 



implies a sum over both particle indices α and β,

with α = β.

Dynamic Correlation

variable function Experiment

v: velocity of a v(t) · v(0) Translational

tagged particle diffusion

: angular 

(t)

(0) Rotational

velocity about the center diffusion

of mass

n(r, t): density (1/N )

ik · (r

(t)−r

(0))

Neutron scattering

(t): position of the (1/N )



ik · (r

(t)−r

(0))

αth particle at t

Polarizability tensor ν

(1/N )

(0)ν

(t)e

ik · (r

(t)−r

(0))

Polarized

Brillouin scattering

Trace ν

(1/N )



(0)ν

(t)e

ik · (r

(t)−r

(0))

Depolarized

Brillouin scattering

with ρ

=ˆρ being the average density. The average densities ρ

= mn

are constants in

the isotropic liquid state. The density–density correlation function involving ﬂuctuations at

two different space and time points is deﬁned as

(|r − r



|, t) = V δ ˆn(r, t)δ ˆn(r



, 0). (1.3.19)

It is often more convenient to describe the density–density correlation function of the

Fourier component of the density variable,

ˆn(k, t) =



dr e

ik · r

ˆn(r, t) = V

−1



ik · r

(t)

. (1.3.20)

The Fourier-transformed correlation function is then deﬁned as

F(k, t) =

δ ˆn(k, t)δ ˆn(−k, 0), (1.3.21)

where V is the volume. Using the above deﬁnition of the density ﬂuctuations, we obtain

that the correlation function F(k, t) can be written in two separate parts involving

40 Statistical physics of liquids

incoherent and coherent parts as follows:

(k, t) =

N 



α,β=1

ik · (r

(t)−r

(0))

, (1.3.22)

(k, t) =



α=1

e

ik · (r

(t)−r

(0))

, (1.3.23)

where the prime indicates that α = β in the sum. The ﬁrst part is often called the distinct

part of density correlation functions while the second part is referred to as the self part of

the correlation function or the van Hove correlation function. The spectral quantity for the

density–density correlation function S(k,ω),

S(k,ω) =

2π



+∞

−∞

F(k, t)e

iωt

dt, (1.3.24)

is called the dynamic structure factor and is measurable in inelastic light-, X-ray-, and

neutron-scattering experiments (Mezei, 1991). The correlation function F (k, t = 0) for

density ﬂuctuations at the same time refers to the structural or thermodynamic property

of the liquid. The static correlation function F(k, t = 0) = n

S(k), where S(k) is the

static structure factor deﬁned in eqn. (1.2.79). In the theories considered in the subsequent

chapters in this book, the implicit effect of the interaction potential for the ﬂuid particles

on the dynamic properties will always be considered in terms of the corresponding static

structure factor and higher-order static correlations.

Another important correlation function for our discussion is the current–current corre-

lation function. The current

g(x, t) is a vector ﬁeld and hence, for an isotropic system, the

corresponding correlation function is divided into a longitudinal part and a transverse part.

The spatial Fourier transform of the correlation function G

(q, t) between g

(x, t) and



, 0) for the isotropic ﬂuid is expressed as

(k, t) =

(k, t) + (δ

−

(k, t), (1.3.25)

with subscripts L and T referring to the longitudinal and transverse parts, respectively. If

we choose both indices i and j of coordinates to be along the direction of the vector k

then

= 1 and G

= G

. If both i and j are in a direction transverse to k then

= G

. On the other hand, if i( j) is along k and j (i ) transverse to k, then G

= 0.

From the continuity equation (1.3.17) and the deﬁnitions (1.3.19) and (1.3.25) it follows

directly that

(k,ω) = k

(k,ω), (1.3.26)

linking the two-sided Fourier transforms of the density and (longitudinal) current autocor-

relation functions.