Das Sh.P. Statistical Physics of Liquids at Freezing and Beyond

Подождите немного. Документ загружается.

1.2 Equilibrium properties 21

The calculation of the thermodynamic pressure P involves computing the derivative of Z

with respect to the volume. The volume dependence of the partition function has two com-

ponents. Let us ﬁrst consider the 3N -dimensional integral over the spatial coordinates. Let

us assume that the volume of the system is a box of size 2L for each dimension and that the

spatial integral is done over the linear range −L to +L. The volume of the system V ∼ L

A change of the integration variables from x to x



= x/L reduces the conﬁguration integral

on the RHS of eqn. (1.2.59) to



−1



...



−L



exp

[

−βU (r

,...,r

)

]

. (1.2.61)

Using this form in eqn. (1.2.60), we obtain for the pressure

N !Z





N −1



−1



...



−L



−βU(r

,...,r

)

−β



...



−βU(r

,...,r

)



∂U

∂V





= n −

N !Z



−βU(r

,...,r

)



∂U

∂V



. (1.2.62)

For systems in which the potential part U of the Hamiltonian involves only two-body

interactions the integral I

virial

(say) in the second term on the RHS is simpliﬁed. In this

case the spatial dependence of U comes through the two-body interaction potential u(r),

U =

N 



i, j=1

u(r

). (1.2.63)

Since the spatial dependence of U comes through that of the two-body potential, we write

the derivative on the RHS in the form

virial

N 



i, j=1



−βU(r

,...,r

)

N !Z





du(r

)



...dr

. (1.2.64)

On changing the integration variable from x to x



= x/L it follows that r

→ V

1/3



and hence the derivative dr

/dV = r

/(3V ). For a system of identical particles all the

different N (N − 1) choices for the pairs in the sum above give the same integral. For the

spherically symmetric potential u(r

) we obtain

virial

N !

(N − 2)!





du(r

)

· r





−βU(r

,...,r

)

N !Z



... dr

2πβ



dr r

du(r )

g(r). (1.2.65)

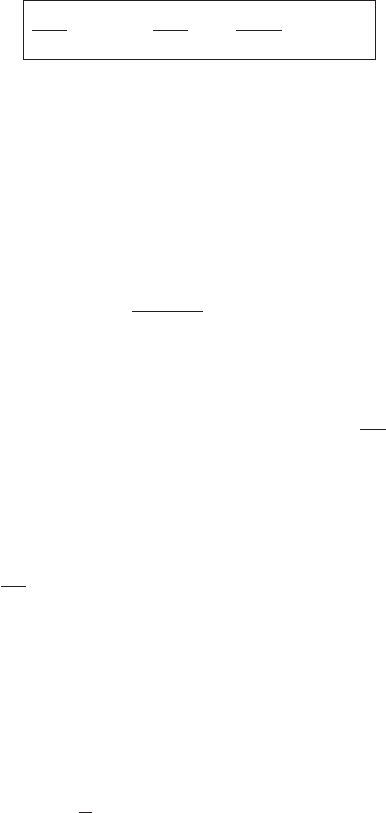
22 Statistical physics of liquids

We obtain the pressure in terms of the pair correlation functions as

= n − n

2πβ



∞

du(r )

g(r)r

dr. (1.2.66)

In the above equation we have dropped the subscript N from g in the thermodynamic limit.

This is termed the virial equation.

The compressibility condition

The isothermal compressibility κ

of the liquid deﬁned in eqn. (1.2.45) is also related to

the pair correlation function g(r). In order to demonstrate this, we integrate with respect to

all the variables {r

, p

}the deﬁnition (1.1.32) of the f

(s)

and obtain, in terms of f

(N )



(s)

) =

N !

(N − s)!



(N )

). (1.2.67)

On taking the s = 2 case, eqn. (1.2.67), and averaging over the number of particles N in

terms of the probability P(N ) deﬁned in eqn. (1.2.39), we obtain



(2)

, r

)



dN P(N )(N

− N ) = N

−

N , (1.2.68)

where the angular brackets imply averaging over the number of particles N in the system.

Using the deﬁnition (1.2.58) for the pair correlation function, the above relation gives us

the mean-square ﬂuctuation of N for an isotropic ﬂuid,

−

N + n



g(r

, r

) −

N + n



dr g(r) −

NnV



1 + n



dr{g(r) − 1}



. (1.2.69)

Now, using the relation (1.2.46), we obtain the compressibility condition

= 1 + n



(g(r) −1)dr. (1.2.70)

Note that the above relation (1.2.70) is obtained from consideration of the grand-canonical

ensemble and, unlike eqn. (1.2.66), is not limited only to pairwise-additive interaction

potentials.

The static correlation function

Starting from the level of N particles, the reduced distribution function giving the condi-

tional probability of ﬁnding a smaller number of particles has been deﬁned in eqn. (1.1.32).

1.2 Equilibrium properties 23

Thus the s-particle (s < N ) reduced distribution function f

(s)

is deﬁned as

(s)

, p

, t) =

N !

(N − s)!



(N )

, p

, t)dr

s+1

... dr

. (1.2.71)

Furthermore, the conditional probability of there being s particles simultaneously at

,...,r

} irrespective of their momenta is obtained from the corresponding f

(s)

integrating out the momentum variables {p

(s)

) =



(s)

, p

) =

N !

(N − s)!



(N )

, p

, t)dp

s+1

... dr

(1.2.72)

where we have used the notation p

≡{p

,...,p

}. Note that the above deﬁnition of

can be rewritten in the form

(s)

, t) =

N !

(N − s)!



(N )

, p

, t){δ(r

−

)...δ(r

−

)}

N 



,...,α

δ(r

−

)...δ(r

−

)

, (1.2.73)

where the prime in the summation in (1.2.73) indicates that none of the α

are equal. The

simplest examples of the above distribution function are the s = 1, 2,...cases,

(1)

(r) =



δ(r − r

)

, (1.2.74)

(2)

(r, r



) =

N 



α,β

δ(r − r

)δ(r



− r

)

, (1.2.75)

and so on, where we have dropped the subscript N on n

(s)

for simplicity and {r

,...,r

}

are now the space coordinates of the particles labeled as α = 1,...,N respectively. Note

that the above deﬁnitions for the average distribution functions are not restricted to systems

in equilibrium.

Let us focus on the simplest of these spatial distribution functions, namely the one-

particle quantity n

(1)

(r), simply written as the ensemble average of ˆn(r),

ˆn(r) =



δ(r − r

), (1.2.76)

where we have put the hat on n to indicate that it depends on the phase-space variables. The

integral of this one-particle density over the whole volume is N , the total number of parti-

cles. For an isotropic ﬂuid in equilibrium in the absence of any external ﬁeld the average

density at every point is a constant so that

ˆn(r)

= N/V = n

. The product of the density

ﬂuctuations δ ˆn =ˆn −n

at two different spatial points but at the same time, averaged over

the equilibrium ensemble, is referred to as the equal-time correlation function. For the ﬂuid

24 Statistical physics of liquids

in equilibrium translation invariance holds and the equal-time correlation function χ

is a

function of (r − r



) only:

(r − r



) =

δ ˆn(r)δ ˆn(r



)



α=1



β=1

δ(r − r

)δ(r



− r

)

− n

= δ(r − r



)



α=1

δ(r − r

)

N 



α,β=1

δ(r − r

)δ(r



− r

)

− n

(1.2.77)

where the prime indicates that the α = β term is dropped from the sum. However, using

now eqns. (1.2.74) and (1.2.75), we obtain from the above equation the result

(r − r



) = n

δ(r − r



) + n

{g(r − r



) − 1}

. (1.2.78)

Now, on taking the Fourier transform (see eqn. (1.3.9) for its deﬁnition) of the eqn. (1.2.78),

we obtain the result

(k) = n



1 + n



dr e

ik · r

{g(r) − 1}



≡ n

S(k), (1.2.79)

where the Fourier transform of the radial distribution function g(r) is expressed in terms

of the Fourier-transformed quantity S(k) for the isotropic liquid,

S(k) = 1 + n



ik · r

h(r)dr, (1.2.80)

with h(r) = g(r) − 1. S(k) is termed the static structure factor for the liquid. This is a

quantity directly measurable from the coherent part of elastic scattering intensities using

a radiation source suitable for the length scale probed in the system. For experimental

methodologies used in scattering experiments see Berne and Pecora (1976) and Hansen

and McDonald (1986).

1.2.4 Integral equations for g(r)

Both (1.2.66) and (1.2.70) give rise to the equation of state for the liquid, via two differ-

ent routes, and in terms of the pair correlation function g(r). Computation of the radial

distribution function g(r) for a liquid thus forms a major part of the study of its equilib-

rium thermodynamic properties. The determination of g(r) is carried out by the solution of

appropriate integral equations. We discuss below the broad outlines of some of the methods

for computing g(r) for a liquid.

The Kirkwood approximation

One of the earlier approaches to computing g(r) comes from the stationary limit of the

BBGKY hierarchy, from which one can obtain a set of equations for the static functions

1.2 Equilibrium properties 25

(s)

deﬁned in eqn. (1.2.56) for the N -particle system. The hierarchy equation for the

s-particle distribution function (in the absence of any external ﬁeld) is obtained from

eqn. (1.1.34) as



i=1

⎡

⎣

⎛

⎝

T ∇

⎧

⎨

⎩

s 



j=1

⎫

⎬

⎭

⎞

⎠

(s)

)

⎤

⎦

=−



i=1





s+1

i,s+1

· f

(s+1)

)



. (1.2.81)

Since eqn. (1.2.81) is independent of s and the value of the momentum p

, the equality

must hold term by term and the space-dependent parts within the square brackets should

be equal. We write the equation now in terms of the spatial distribution functions n

(s)

)

as follows:



T ∇

(s)

) =−



s+1

1,s+1

· n

(s+1)

), (1.2.82)

where we have used the notation

s 



l=1

s 



l=1

∇

u(r

, r

) (1.2.83)

and ∇

represents the derivative with respect to r

. Now, using the deﬁnition (1.2.56) for

the s-particle distribution function g

(s)

), we obtain the hierarchy equations

−k

T ∇

(s)

) =

s 



l=1

∇

u(r

, r

(s)

)

+ n



∇

u(r

, r

s+1

(s+1)

s+1

)dr

s+1

. (1.2.84)

The set of equations described by (1.2.84) is known as the Yvon–Born–Green (YBG) hier-

archy. To solve this, a suitable closure scheme is needed. For an isotropic ﬂuid the ﬁrst

equation of this set, i.e., the s = 2 case, reduces to an integral equation for g

, r

) of

the form (we drop the superscript s for simplicity)

T ∇

, r

) + g

, r

)∇

u(r

, r

) =−n



∇

u(r

, r

)dr

(1.2.85)

The hierarchy is closed by writing the function g

(3)

, involving three particles, in the

Kirkwood superposition approximation (Kirkwood, 1935)as

(3)

, r

) = g

(2)

, r

(2)

, r

(2)

, r

). (1.2.86)

26 Statistical physics of liquids

For the isotropic liquid the pair correlation function depends only on the distance between

the two points, g

, r

) ≡ g

).Using(1.2.86) in eqn. (1.2.85), we obtain the

following equation:

∇

T ln[g

)]+u(r

)}=−n



∇

u(r

){g

) − 1}g

). (1.2.87)

The last term added on the RHS gives a vanishing contribution since for the isotropic liquid

every point is equivalent on average, and hence



u(r

, r

) = 0. (1.2.88)

The integral equation (1.2.87) known as the Yvon–Born–Green equation is good for com-

puting the pair correlation functions in a low-density ﬂuid. Once g(r) is known, the other

thermodynamic properties readily follow, as discussed above. For systems interacting with

two-body potentials the integral-equation approach has been applied widely and the corre-

sponding theoretical formulation of the problem is speciﬁc to the nature of the interaction.

We discuss below the broad outlines of the calculation of the pair correlation function for

two generic cases: (a) for a short-range repulsive potential like the hard-sphere interaction;

and (b) for an interaction having an attractive part effective over a long distance.

Hard-sphere interaction

Subsequent to the Kirkwood approximation for closing the hierarchy, a new class of inte-

gral equations for g(r) was obtained for ﬂuids interacting through a pairwise additive

potential by considering different methods of closing the hierarchy. This involved introduc-

ing a new type of correlation function, termed the direct correlation function c(r), which

was deﬁned from the Ornstein–Zernike relation (Ornstein and Zernike, 1914),

h(r) = c(r) + n



c(|r −r



|)h(r



)dr



. (1.2.89)

Note that from eqn. (1.2.79) it follows that eqn. (1.2.89) also leads to the relation

S(k) =[1 −n

c(k)]

−1

. (1.2.90)

To solve for g(r) and c(r), for a given pair potential u(r), eqn. (1.2.89) is supplemented

with a closure relation. Two standard prescriptions for this, namely the Percus–Yevick (PY)

(Percus and Yevick, 1958) solution and hypernetted chain closure (HNC) (van Leeuwen

et al., 1959), respectively, give

y(r) = 1 + h(r) − c(r)(PY), (1.2.91)

y(r) = exp[h(r) − c(r)] (HNC), (1.2.92)

1.2 Equilibrium properties 27

where the function y on the LHS is deﬁned as y(r) = e

βu(r)

g(r). The motivation for both

of the proposed closures can be reached through different approaches, for which we refer

the reader to Percus (1962, 1964) and Stell (1963). Of the two proposed closures, the PY

solution is most suitable for describing the correlations between particles when the inter-

action potential is harshly repulsive or of short range. The hard-sphere potential is a typical

example of this. The HNC, on the other hand, is well suited for long-range potentials such

as Coulombic systems. However, for strongly coupled systems like high-density or low-

temperature liquids, both these closures lead to severe thermodynamic inconsistency since

the virial and compressibility equations given by (1.2.66) and (1.2.70), respectively, lead

to different equations of state.

For investigating equilibrium theories of simple liquids, the hard-sphere system has been

the most widely studied system, both through computer simulations and using theoretical

methods. For the hard-sphere system the integral equation for g(r) can be solved exactly.

The hard-sphere potential is given by

(r) =

∞ for r ≤ σ,

0forr >σ.

(1.2.93)

Since the barrier height is inﬁnite, with the hard-sphere potential g(r) = 0forr ≤ 0 and

g(r) = y(r) for r ≥ 0. The PY closure eqn. (1.2.91) in this case takes the form

c(r) =

−y(r) for r ≤ σ,

0forr≥σ.

(1.2.94)

With the above closure relation the Ornstein–Zernike equation (1.2.89) is solved using

Laplace-transform methods and the direct correlation function is obtained as (Wertheim,

1963, 1964; Thiele 1963)

c(x) =

−α

− α

(r/σ ) − α

(r/σ )

for r ≤ σ,

0forr >σ.

(1.2.95)

The constants α

appearing in eqn. (1.2.95) are obtained in terms of the packing fraction

ϕ = πnσ

/6 as follows:

(1 + 2ϕ)

(1 − ϕ)

, (1.2.96)

=−6ϕ

(1 + ϕ/2)

(1 − ϕ)

, (1.2.97)

ϕα

. (1.2.98)

Often it is more convenient to express the Fourier transform of the above expression in such

a way as to obtain the static structure factor S(k) using the relation (1.2.90) (see Fig. 1.3).

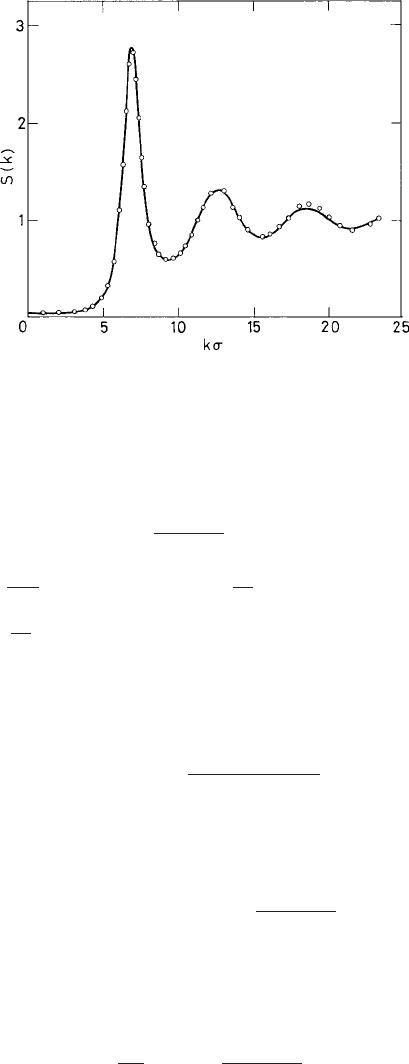
28 Statistical physics of liquids

Fig. 1.3 The static structure factor from MD simulations of Lennard-Jones system at T = 0.723 and

ρ = 0.844 (dots). The solid line corresponds to the hard-sphere mdoel.

Thus the Fourier transform of (1.2.95) gives the result (Ashcroft and Lekner, 1966)

nc(kσ) =−4πnσ



ds s



sin(skσ)

skσ



{α

+ α

s +α

}

=−

24ϕ



(sin x − x cos x) +

{2x sin x − (x

− 2)cosx − 2}

{(4x

− 24x)sinx − (x

− 12x

+ 24)cosx + 24}

(1.2.99)

in terms of the dimensionless variable x = kσ . The above result is useful in obtaining the

compressibility of the hard-sphere ﬂuid using the relation

nc(0) =−ϕ

(4 − ϕ)(2 +ϕ

)

(1 − ϕ)

(1.2.100)

and hence, from eqn. (1.2.90) for the corresponding static structure factor, S(0) is

obtained as

−1

(0) = 1 −nc(0) =

(1 + 2ϕ)

(1 − ϕ)

. (1.2.101)

Since the compressibility is expressed as κ

−1

= n(∂ P/∂n), we obtain from the compress-

ibility condition, i.e., eqn. (1.2.70), the relation



∂ P

∂n



= β

−1

(1 + 2ϕ)

(1 − ϕ)

. (1.2.102)

1.2 Equilibrium properties 29

By integrating the above expression we obtain the equation of state from the compressibil-

ity equation as

1 + ϕ +ϕ

(1 − ϕ)

. (1.2.103)

On the other hand, we obtain the equation of state directly from eqn. (1.2.66), giving that

β P = n −n

2πβ



∞

du(r )

g(r)r

= n + n

2π



∞

δ(r − σ)g(r)r

= n

1 + 4ϕg(σ )

. (1.2.104)

In reaching the above result we used the fact that the discontinuous hard-sphere potential

(r) given by eqn. (1.2.93) decreases discontinuously from ∞ to 0 as r increases from

−

to σ

. Hence the derivative β du(r)/dr =−δ(r −σ). The pair correlation function at

contact g(σ ) directly follows from the PY closure. In the limit r → σ

, g(r) = 0 while

c(r) = 0. On the other hand, for r → σ

−

, g(r) = 0 while c(r) = 0. Since the function

y(r) is continuous through r = σ , we obtain from eqn. (1.2.91) that g(σ

) =−c(σ

−

).It

then follows from eqn. (1.2.95) that

g(σ ) = α

+ α

1 + ϕ/2

(1 − ϕ)

(1.2.105)

and hence the corresponding equation of state is obtained from eqn. (1.2.104):

1 + 2ϕ +3ϕ

(1 − ϕ)

. (1.2.106)

The two different equations of state given by (1.2.103) and (1.2.106) matchuptoO(ϕ

beyond which the difference grows. An accurate equation of state for a hard-sphere system

has been developed by studying the Mayer cluster expansion for such a system. The latter

is generally deﬁned as

= 1 +

∞



i=2

(T )n

i−1

(1.2.107)

in terms of virial coefﬁcients B

. These coefﬁcients can be computed order by order using

cluster diagrams. In fact, for the hard-sphere system B

, B

, and B

are known analytically.

However, the complexity of the calculation increases rapidly with the order. The numbers

of diagrams entering the computation of B

for i = 2,...,6 are, respectively, 1, 3, 10,

56, and 468. Explicit calculations are therefore limited to low orders. For the hard-sphere

30 Statistical physics of liquids

system this calculation has been extended to B

(van Rensburg, 1993; Vlasov et al., 2002)

to obtain

= 1 + 4ϕ + 10ϕ

+ 18.365ϕ

+ 28.325ϕ

+ 39.74ϕ

+ 53.5ϕ

+ 70.8ϕ

+···

≡ 1 +

∞



m=1

. (1.2.108)

The above series has been summed by making the useful observation that the ﬁrst seven

terms on the RHS are well reproduced if the coefﬁcient C

is approximated with the

formula

= 3m + m

. (1.2.109)

The coefﬁcients evaluated with this formula are C

=4 (4), C

=10 (10), C

18 (18.365), C

= 28 (28.325), C

= 40 (39.74), C

= 54 (53.5), and C

= 70 (70.8),

where the numbers in parentheses are the actual values of the coefﬁcient in the series

presented in eqn. (1.2.108). The formula (1.2.109) for C

is therefore taken as a good

approximation for the virial coefﬁcient to all orders. We obtain the series in the form

= 1 +

∞



m=1

+ 3m)ϕ

. (1.2.110)

The sums can be easily evaluated using the results

∞



m=1

mϕ

= ϕ

dϕ

∞



m=1

(1 − ϕ)

, (1.2.111)

∞



m=1



dϕ



∞



m=1

ϕ(1 +ϕ)

(1 − ϕ)

. (1.2.112)

On evaluating the series on the RHS of eqn. (1.2.110) with the results (1.2.111) and

(1.2.112), we obtain the equation of state as

1 + ϕ +ϕ

− ϕ

(1 − ϕ)

. (1.2.113)

which is termed the Carnahan–Starling equation of state (Carnahan and Starling, 1969;

Mansoori et al., 1971). Though it was obtained in an ad-hoc manner in the above simpliﬁed

analysis, eqn. (1.2.113) presents a very accurate equation of state valid for a hard-sphere

liquid up to high packing fractions close to freezing, having discrepancies from molecular-

dynamics simulation results of at most around 1%. The predictions from this equation

of state lie in between those from the other two equations of state given by (1.2.103) and

(1.2.106), respectively, following from the compressibility condition (1.2.70) and the virial

equation (1.2.66). This is shown in Fig. 1.4. Several other equations of state have been

devised (Mulero et al., 1999), though the form (1.2.113) is the simplest and most widely