Das Sh.P. Statistical Physics of Liquids at Freezing and Beyond
Подождите немного. Документ загружается.


2.1 The density-functional approach 61
where H
0
N
is the intrinsic part of the Hamiltonian in which U(r
1
,...,r
N
) is the inter-
action energy of the N -particle system – as has already been introduced in Chapter 1
in eqn. (1.1.16). U
ext
is the external field contribution and is expressed in terms of the
interaction with a local field obtained from a one-body potential φ, U
ext
=
5
α
φ(r
α
).Fol-
lowing the example of equilibrium statistical mechanics, we define the functional [f ] of
f (r
N
, p
N
) as
[ f ]=Tr f (H
N
− μN + β
−1
ln f ), (2.1.2)
where μ is the chemical potential and β = 1/(k
B
T ) denotes the inverse temperature char-
acterizing the grand-canonical ensemble. The symbol Tr in (2.1.2) refers to the classical
trace defined in terms of the integration of the phase-space variables (r
N
, p
N
) (defined in
(1.2.3))as
Tr ≡
∞
N =0
1
h
3N
N !
dr
1
...
dr
N
dp
1
...
dp
N
. (2.1.3)
If we choose f (r
N
, p
N
) to be a trial distribution function representing the probability of
the system in the phase-space region (r
N
, p
N
), then, according to the above definition,
Tr f (r
N
, p
N
) = 1. (2.1.4)
The external field contribution U
ext
, which is a sum of single-particle contributions, is
expressed as an integral,
U
ext
=
N
α=1
φ(r
α
) =
dx ˆn(x)φ(x), (2.1.5)
in terms of the microscopic one-particle density ˆn. At the microscopic level, the one-
particle density ˆn(x) is formally defined as a function of the phase-space variables
(r
N
, p
N
),
ˆn(x) =
N
α=1
δ(x − r
α
). (2.1.6)
The average density function corresponding to the distribution function f is then obtained
as n(x) = Tr ˆn(x) f .
The density-functional model uses the equilibrium averaged density as the order param-
eter. The statistical-mechanical formulation of the problem is often conveniently done in
terms of the grand-canonical ensemble, implying that the volume of the system remains
constant while the number of particles changes. The equilibrium (McQuarie, 2000) distri-
bution function f
0
corresponding to this ensemble is obtained as
f
0
=
−1
exp[−β(H
N
− μN )], (2.1.7)
where (β, μ) is the grand-canonical partition function. Using (2.1.7) for f
0
in the defini-
tions (2.1.2) and (2.1.4) it follows that
[ f
0
]=−β
−1
ln (β, μ) =
EQ
, (2.1.8)

62 The freezing transition
where
EQ
is the equilibrium grand potential for the system.
EQ
=−PV, where P
and V , respectively, denote the pressure and volume of the system in equilibrium. The
corresponding density n
0
(x) is obtained by averaging over the grand-canonical ensemble,
n
0
(x) = Tr ˆn(x) f
0
=
δ ln
δβu(x)
, (2.1.9)
where u(x) = μ − φ(x). For any arbitrary distribution function f satisfying the normal-
ization (2.1.4) the corresponding functional [ f ] is obtained as
[ f ]=Tr f (H
N
− μN + β
−1
ln f )
= [f
0
]+β
−1
Tr[f ln( f / f
0
)]
>[ f
0
]=
EQ
. (2.1.10)
Two points are to be noted with respect to the above results.
(a) The second equality in (2.1.10) is obtained using the definition of the grand-canonical
ensemble being restricted to those distribution functions f for which the ensemble
average of the Hamiltonian H
N
and the number of particles N remain fixed.
(b) The last inequality in (2.1.10) follows from the fact that Tr[f ln( f/f
0
)] is always
positive. To see this, we consider
Tr[f ln( f / f
0
)]=
∞
N =0
1
N !
d f
0
()
[
x ln(x)
]
=
∞
N =0
1
N !
d f
0
()
[
x ln(x) − x + 1
]
, (2.1.11)
where we define f ()/ f
0
() ≡ x (say) with d denoting the elementary volume in the
6N -dimensional phase space. The last equality in eqn. (2.1.11) follows since both f ()
and f
0
() are normalized (see eqn. (2.1.4)), canceling out the last two terms on the
RHS. According to the Gibbs inequality (see Appendix A1.1) the quantity within the
square brackets on the RHS of eqn. (2.1.11) is always positive and hence the integral
is also positive definite. Therefore the functional [ f ] attains its minimum value for
the choice f = f
0
.
We now consider the following question: can two different external potentials φ and φ
cor-
respond to the same equilibrium density n
0
(x)? Let the equilibrium distribution functions
with two such external potentials be f
0
and f
0
, respectively. The Hamiltonian correspond-
ing to the external potential φ
is denoted as
H
N
= H
0
N
+U
ext
, (2.1.12)
where U
ext
=
5
α
φ
(r
α
). The functional [ f ] now has its minimum value for the corre-
sponding equilibrium distribution f = f
0
. By comparing the values of the functional
2.1 The density-functional approach 63
corresponding to f = f
0
and f
0
, respectively, we obtain the inequality
EQ
= Tr f
0
(
H
N
− μN + β
−1
ln f
0
)
< Tr f
0
(
H
N
− μN + β
−1
ln f
0
)
=
EQ
+
dx n
0
(x)[φ
(x) − φ(x]. (2.1.13)
The inequality in the second line of (2.1.13) follows from the fact that the choice f
0
min-
imizes the functional [f ] in this case. To simplify the analysis we assume the chemical
potentials both in the primed and in the unprimed cases to be the same μ. The above argu-
ment also applies in the reverse order on interchanging the primed and unprimed quantities,
i.e., we evaluate the functional [ f ]first for f = f
0
corresponding to the Hamiltonian H
N
with external potential φ to obtain the inequality
EQ
<
EQ
+
dx n
0
(x)[φ(x) −φ
(x)]. (2.1.14)
On adding (2.1.13) and (2.1.14) we obtain the contradictory result
EQ
+
EQ
<
EQ
+
EQ
. Therefore the original assumption linking φ(x) and φ
(x) to the same n
0
(x) is not
valid. We have thus proved the important result that the equilibrium density n
0
(x) is
uniquely determined by the external potential φ(x). The inverse, i.e., a given n
0
(x) uniquely
determining the corresponding field φ(x), also holds in the DFT description for the ther-
modynamic state. This is implied from the finite-temperature generalization (Mermin,
1965) of the ground-state theorem (Hohenberg and Kohn, 1964). On the other hand, from
(2.1.8) it follows that for a given system characterized by H
0
N
, i.e., by the corresponding
interaction U (as defined in (2.1.1), the equilibrium distribution function f
0
is entirely
determined by the external potential φ(x). On combining these two results we obtain that
the equilibrium distribution function f
0
is uniquely determined by the one-particle density
n
0
(x).
Using the unique correspondence between f
0
and n
0
, a functional
φ
of the one-particle
density n(x) for the system in an external potential φ is obtained as
φ
[n]=[ f ]≡Tr f (H
N
− μN + β
−1
ln f ). (2.1.15)
In terms of
φ
[n] we further define a functional F[n(x)],
φ
[n]=F[n]+
dx φ(x)n(x) − μ
dx n(x)
= F[n]−
dx n(x)u(x), (2.1.16)
where u(x) is as defined above with eqn. (2.1.9). It follows directly from the definition
(2.1.2) for [ f ] that F [n] is obtained from the corresponding distribution function f as
F[n(x)]=Tr f
(
H
0
N
+ β
−1
ln f
)
. (2.1.17)

64 The freezing transition
For the equilibrium distribution f = f
0
the corresponding one-particle density is n
0
(x),
and we obtain for the value of
φ
[n
0
]
φ
[n
0
]≡[ f
0
]=
EQ
. (2.1.18)
For any other f = f
0
since [ f ] is higher, i.e., [f ] >[f
0
].Ifn(x) is the one-particle
density corresponding to f , we must have then
φ
[n] >
φ
[n
0
]. Thus we reach the impor-
tant result that the equilibrium density n
0
(x) minimizes the functional
φ
[n] and its value
at the minimum is equal to the equilibrium grand potential. This result is conveniently
expressed in terms of the functional variational principle,
δ
φ
[n]
δn(x)
n(x)=n
0
(x)
= 0. (2.1.19)
Note that, if we were considering the canonical ensemble, then it would follow in an exactly
similar manner that the corresponding functional (of density) to be minimized would be the
one involving the first two terms on the RHS of (2.1.16).
F
φ
[n]=F[n]+
dx n(x)φ(x). (2.1.20)
For the equilibrium density n
0
(x) the minimum value of this functional F
φ
[n] is equal
to the Helmholtz free energy of the system much in the same way as
φ
[n] is equal to
the grand potential
EQ
for the grand-canonical ensemble considered above. The results
(2.1.18) and (2.1.19) form the basis for calculation of the equilibrium densities in studying
the freezing transition. This is described next.
2.1.2 An approximate free-energy functional
Having identified the thermodynamic extremum principle we now construct the proper
free-energy functional F[n] in terms of the density n(x). This functional is then used to
determine the appropriate inhomogeneous density function n
0
(x) at equilibrium satisfying
the extremum principle (2.1.21). Using the definition (2.1.16) and the extremum condition
(2.1.19), we obtain the result
δF[n]
δn(x)
n=n
0
= μ − φ(x) ≡ u(x). (2.1.21)
The free-energy function F[n] has contributions from two different parts,
F = F
id
+ F
ex
, (2.1.22)
to be defined as follows.
(a) The ideal-gas part F
id
is the free-energy functional for a noninteracting system of
particles.
(b) The excess part F
ex
is due to interaction between the particles.

2.1 The density-functional approach 65
The ideal-gas part
F
id
[n] as a functional of density n(x) is obtained by using the definition (2.1.20).This
also involves obtaining the functional relation between the equilibrium density and the
field u(x). For the ideal-gas case with the interaction potential U = 0 this can be done
exactly. In this case H
0
N
has only the kinetic-energy term K =
5
α
p
2
α
/(2m) and hence,
on explicitly integrating out the 3N momentum variables, the grand-canonical partition
function is obtained as
= Tr exp
−β
&
H
0
−
α
u(r
α
)
'
=
∞
N =0
1
N !
−3
0
dx e
βu(x)
N
= exp
−3
0
dx e
βu(x)
, (2.1.23)
where
0
= h/
√
2πmk
B
T is the de Broglie or thermal de Broglie wavelength for the
liquid particles. From eqns. (2.1.9) and (2.1.23) one obtains for the noninteracting case the
equilibrium density for the inhomogeneous state in the presence of the field φ(x) as
n
0
(x) =
exp[βu(x)]
3
0
, (2.1.24)
i.e., βu(x) = ln
!
3
0
n
0
(x)
"
. We obtain the free-energy functional F [n
0
] by evaluating the
expression (2.1.16) at n = n
0
as
β F
id
[n
0
]=
dx n
0
(x)
ln
#
3
0
n
0
(x)
$
− 1
, (2.1.25)
where we have used for the ideal-gas equation of state
−β
EQ
= β PV =
¯
N ≡
dx n
0
(x) (2.1.26)
for the average number of particles
¯
N .
We choose the ideal-gas part of the free energy F
id
[n]as a functional of the density func-
tion n(x) such that for the equilibrium density n(x) = n
0
(x) it reduces to the expression
(2.1.25) for F
id
[n
0
]. F
id
[n] is thus obtained by generalizing the above result as
F
id
= β
−1
dx n(x)
ln
(
3
0
n(x)
)
− 1
. (2.1.27)
The equilibrium density for the noninteracting system is obtained as
n
0
(x) = z exp[−βφ(x)], (2.1.28)
where the normalization constant z = exp(βμ)/
3
0
.

66 The freezing transition
The ideal-gas part of the free energy is an entropic contribution. See also Appendix A1.1
for a deduction of F
id
for a coarse-grained density function n(x) using an occupation-
number representation. It follows from the result (2.1.27) that an inhomogeneous density
function implies a higher degree of mass localization and hence reduction of entropy. For
asystemofN particles the difference between the F
id
values corresponding to a uniform
state of density n
0
and one with an inhomogeneous density distribution n(x) is given by
β F
id
= n
0
dx ˜n(x)[ln ˜n(x)], (2.1.29)
where we assume that ˜n(x) = n(x)/n
0
. Since by definition ˜n(x) is always positive, from
the Gibbs inequality (see Appendix A1.1) it follows that
dx
!
˜n(x)ln ˜n(x) −˜n(x) + 1
"
≥ 0 (2.1.30)
for any density distribution n(x). For a fixed number of particles we have
6
dx[˜n(x) −
1]=0, we have from the relation (2.1.29) F
id
≥0. Entropy always drops upon local-
ization of the particles in a state with inhomogeneous density profiles, as a result of the
restriction of available phase space.
The interaction part
For the interacting system we include in F the contribution from the excess part of the free
energy F
ex
. The functional-extremum principle (2.1.21) now reduces to the form
ln
3
0
n
0
(x)
− c
(1)
(x;n
0
) = β{μ − φ(x)}=βu(x), (2.1.31)
where we have used the definition
β
−1
c
(1)
(x;n
0
(x)) =
δF
ex
δn(x)
n(x)=n
0
(x)
. (2.1.32)
Using the result (2.1.31), we obtain for the equilibrium density n
0
(x)
n
0
(x) = z exp[−βφ(x) +c
(1)
(x;n
0
(x))], (2.1.33)
showing that c
(1)
(x;n
0
(x)) acts as a one-body potential due to the interaction between
the fluid particles. The higher-order direct correlation functions are defined in terms of
functional derivatives of c
(1)
with respect to n
0
(x). We demonstrate in Appendix A2.1 that
the two-point function c
(2)
(x
1
, x
2
) is related to the pair correlation function g
(2)
(x
1
, x
2
) in
the fluid by a relation that reduces to the Ornstein–Zernike relation for the uniform liquid
discussed in Chapter 1.
The expression for the one-body potential in (2.1.33) is simplified by expanding it
around its value c
l
for the uniform liquid state of density n
l
=
¯
N /V . For the uniform
liquid in the absence of any external field we have from eqn. (2.1.33) for the uniform den-
sity n
l
= z exp(c
l
). The inhomogeneous density function n
0
(x) is then obtained in terms
2.1 The density-functional approach 67
of the corresponding one-particle direct correlation function c
(1)
(r),
n
0
(x) = n
l
exp
#
c
(1)
(x;n
0
(x)) − c
l
− βφ(x)
$
. (2.1.34)
A simple Taylor expansion for c
(1)
(x;n
0
(x)) around the uniform liquid state gives
c
(1)
[x
1
;n
0
(x)]=c
l
(n
l
) +
dx
2
c
(2)
[x
1
, x
2
;n
l
]δn
0
(x
2
)
+
1
2
dx
2
dx
3
c
(3)
[x
1
, x
2
, x
3
;n
l
]δn
0
(x
2
)δn
0
(x
3
) +···, (2.1.35)
where δn
0
(x) = n
0
(x) − n
l
is the fluctuation of the equilibrium density in the inhomoge-
neous state from the uniform liquid-state density n
l
.Ineqn. (2.1.35) we use the following
definitions for the direct correlation functions c
(i)
as the successive functional derivatives
of F
ex
evaluated at the liquid-state density n
l
,
c
(i)
(x
1
,...,x
i
;n
l
) =
δ
i
F
ex
δn(x
1
)...δn(x
i
)
n=n
l
. (2.1.36)
For practical calculations one usually adopts the simplest approximation, keeping terms
only up to the second-order term (i = 2) in the expansion (2.1.35) to obtain the following
expression for the inhomogeneous density in equilibrium:
n
0
(x
1
) =¯n
l
exp
dx
2
c
(2)
(x
1
, x
2
;n
l
)δn
0
(x
2
)
, (2.1.37)
where we identify ¯n
l
= z exp[−βφ + c
l
]≡n
l
exp[−βφ].Foreqn. (2.1.37) the trivial
solution is then the uniform density n
0
(x
1
) = n
l
in the absence of any external field. The
solution of eqn. (2.1.37) is the starting point for the subsequent analysis for testing the pos-
sibility of an inhomogeneous density state. The two-point kernel function c
(2)
(x
1
, x
2
;n
l
)
which is defined in terms of the functional derivative of the one-body potential c
(1)
is
required in order to completely specify eqn. (2.1.37) for the inhomogeneous density. The
excess free energy in the solid state F
ex
is expressed as a functional Taylor expansion
(Courant and John, 1965; Abramowitz and Stegun, 1970) in the density fluctuations
δn
0
(x) =n
0
(x) −n
l
,
F
ex
= F(n
l
) −
dx
1
c
(1)
(x
1
;n
l
)δn
0
(x)
−
1
2
dx
1
dx
2
c
(2)
(x
1
, x
2
;n
l
)δn
0
(x
1
)δn
0
(x
2
) +···. (2.1.38)
The series involves the functions c
(i)
defined in (2.1.36) at the liquid-state density
n
0
(x) =n
l
. In the present case we have only kept terms up to second order in the density
difference.
68 The freezing transition
2.1.3 The Ramakrishnan–Yussouff model
We now discuss the density-functional approach to the freezing transition of an isotropic
liquid into a crystalline state, using an order-parameter description in terms of the density.
We begin with the eqn. (2.1.37) for the inhomogeneous density function n(x) obtained
from the functional extremum principle (2.1.19). This equation is solved using the kernel
function c(x
1
, x
2
) ≡ c(|x
1
− x
2
|) for the isotropic homogeneous liquid state with density
n
l
. The stable solid state at freezing is identified from the solution of the implicit relation
(2.1.37) obtained by using test density functions corresponding to a chosen lattice struc-
ture. The present theoretical approach therefore does not solve the problem of spontaneous
breaking of the translational symmetry; rather it allows one to identify the crystal symme-
try in the inhomogeneous state by picking up the appropriate density function n
0
(x) which
satisfies the functional extremum principle (2.1.19). The density function defined with a
suitable parametrization constitutes the order parameter of the transition. In this regard
there are two main choices for the test density function that have been made in the liter-
ature and will be considered below. Before discussing specific details of the solution, we
first outline the general scheme of locating the freezing-transition point.
At low densities there is only one trivial solution, n(x) = n
l
,ofeqn. (2.1.37) refer-
ring to the homogeneous liquid state. For densities n
l
above a certain value n
∗
l
(dependent
on the temperature T and the chemical potential μ of the liquid), inhomogeneous solu-
tions n(x) with spatially periodic densities corresponding to one or more crystalline states
are possible. Such inhomogeneous solutions are obtained for a continuous range of den-
sities above n
∗
l
above which for every n
l
there is a corresponding inhomogeneous state
with density n
0
(x). The homogeneous state and the inhomogeneous state are at the same
temperature and chemical potential. The particular pair which represents true phase coex-
istence is then chosen from the corresponding Maxwell construction (Huang, 1987)inthe
present case of a grand-canonical ensemble. In the context of liquid–vapor transition the
total number of particles N remains fixed, and for the isobaric ensemble the correspond-
ing Gibbs free energies of the two states are equal. In the grand-canonical ensemble for
the density-functional theory considered here, the volume V is fixed and the correspond-
ing thermodynamic potential which is minimized is the grand potential . The coexisting
states with respective densities n
l
and n
0
(x) have the same temperature T and chemical
potential μ. The location of the true transition point is inferred by equating the grand
potentials in the two states. The difference between the grand potentials in the inhomoge-
neous crystalline state with density n
0
(x) and the homogeneous liquid state with density
n
l
(in the absence of the external potential φ) is obtained as
≡ [n
0
(x)]−[n
l
]
= F
id
[n
0
(x)]+F
ex
[n
0
(x)]−μ
dx[n
0
(x) − n
l
]. (2.1.39)
The difference F
id
= F
id
[n
0
(x)]−F
id
(n
l
) in the ideal-gas part of the free energy is
directly calculated from (2.1.27). The difference F
ex
= F
ex
[n
0
(x)]−F
ex
(n
l
) between
2.1 The density-functional approach 69
the excess free energies of the liquid and solid states is expressed as a functional Taylor
expansion in the density fluctuations δn
0
(x) = n
0
(x) − n
l
from (2.1.38) as
F
ex
=−
dx
1
c
(1)
(x
1
;n
l
)δn
0
(x)
−
1
2
dx
1
dx
2
c
(2)
(x
1
, x
2
;n
l
)δn
0
(x
1
)δn
0
(x
2
) +···. (2.1.40)
On substituting (2.1.40) into (2.1.39) and using the relation (2.1.31) for the case in which
the external field φ = 0, we obtain the following result for the grand potential difference
between the crystalline and liquid states:
=
dx
1
n
0
(x
1
)ln
n
0
(x
1
)
n
l
−
dx
1
(n
0
(x
1
) − n
l
)
−
1
2
dx
1
dx
2
c
(2)
(x
1
, x
2
;n
l
)δn
0
(x
1
)δn
0
(x
2
) −···. (2.1.41)
Therefore, by equating in (2.1.41) to zero the the coexisting density at the freezing-
transition point is obtained. Since the volume V is kept constant, the equality of the grand
potential =−PV for the two states also implies the equality of pressure P. In summary,
among all pairs of points with equal temperature and chemical potential, the one with equal
pressure (up to the same order in perturbation theory) marks the phase-transition point. This
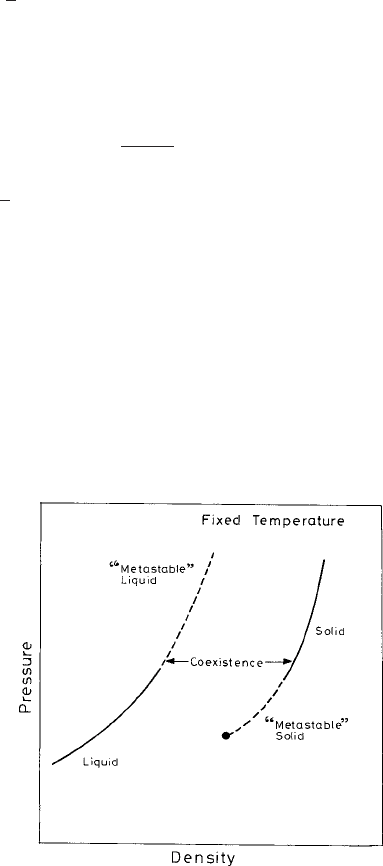
identification is displayed schematically in Fig. 2.1 with a phase diagram.
In the scheme described above for locating the freezing point of the liquid into a crystal,
a crucial ingredient is the choice of the test density function which involves the order
parameters of the associated thermodynamic phase transition. Two functional forms for
Fig. 2.1 The density-functional theory in the grand-canonical ensemble relates each of the liquid
states to a corresponding solid state having the same chemical potential and temperature. (Schematic
diagram from Haymet and Oxtoby (1986).)
c
American Institute of Physics.

70 The freezing transition
the density have been used extensively in the existing literature. The formulation originally
adopted by Ramakrishnan and Yussouff (1979)aswellasbyHaymet and Oxtoby (1981)
and Oxtoby and Haymet (1982) uses the expansion in the reciprocal-lattice-vector (RLV)
space. The first choice for the density function in terms of RLVs is described in some
detail below to clarify the dependence of the order parameter on the lattice symmetry of
the crystal structure. It is also useful for the discussion on the nucleation process for the
growth of the crystal phase, which will be described in the next chapter. The second choice
for the density function in terms of the Gaussian profiles located at the lattice points is
discussed in the next section together with the weighted-density-functional theories.
In the Ramakrishnan–Yussouff theory the solid-state density with underlying crystal
symmetry is expressed exactly in terms of an order-parameter expansion,
n
0
(x) = n
l
1 + η +
∞
m=1
A
m
e
iK
m
· x
. (2.1.42)
The sum in (2.1.42) is over the RLVs {K
m
}of the corresponding crystal structure (Ashcroft
and Mermin, 1976) being tested. The amplitudes A
m
represent the order parameters of the
transition. If all of the A
m
and η are set to zero, the uniform liquid state is obtained. The
average density of the solid state is defined as
n
s
=
1
V
dx n
0
(x). (2.1.43)
η = (n
s
−n
l
)/n
l
denotes the fractional change in density at freezing. Using the expansion
(2.1.42) for the density function, the integral in the exponent on the RHS in (2.1.37) is
obtained as
dx c(x −x
)δn
0
(x
) =˜c
0
η +
∞
m=1
˜c
m
A
m
e
iK
m
· x
. (2.1.44)
We have simplified the notation above by defining the dimensionless quantity ˜c
m
≡
n
l
c(|K
m
|) (for m = 0, 1,...), where c(K
m
) is the Fourier transform of the direct cor-
relation function c(r) of the uniform liquid evaluated at the RLV K
m
. For the isotropic
liquid ˜c
m
is a function only of the magnitude of the wave vector. At the phase-transition
point the grand potentials for the two phases are equal. In Appendix A2.2, the expression
(2.1.41) for the difference of the thermodynamic potential between the two phases is
obtained in terms of the order parameters η and A
m
:
= n
l
V
⎡
⎣
( ˜c
0
− 1)η +
1
2
˜c
0
η
2
+
1
2
m=0
ξ
2
m
˜c
m
⎤
⎦
, (2.1.45)
where ξ
m
denotes the rescaled amplitudes defined as ξ
m
=˜c
m
A
m
.
A nonzero set of solutions for the amplitude parameters in the inhomogeneous density
function (2.1.42) from the above DFT equations marks a stable crystalline phase. The
amplitudes η and A
m
corresponding to the crystalline state in which the liquid freezes are
obtained with the following two inputs.
