Das Sh.P. Statistical Physics of Liquids at Freezing and Beyond

Подождите немного. Документ загружается.

2.4 Applications to other systems 91

used to describe the crystalline state has been modiﬁed to include the presence of vacancy

defects in a crystal and obtains an estimation of the equilibrium density of vacancies. Here

the basic interaction potential between the particles is the only input used in the theory. A

general description of these extensions can be found in Henderson (1992). In the present

section we discuss two important applications linked to the basic theme of this chapter,

namely the study of systems with long-range attractive forces and the nature of liquid–solid

interfaces.

2.4.1 Long-range interaction potentials

So far we have discussed the density-functional theories of the freezing of a hard-sphere

ﬂuid. Geometric packing considerations play an important role in determining the ther-

modynamic properties of the condensed state. However, inclusion of only the hard-core

form of the interaction potential in the Hamiltonian is inadequate for understanding the

symmetry-breaking transition in real systems and hence consideration of more physical

interactions is required. The crystalline phase is generally characterized by strong coher-

ence, which is absent in the hard-sphere case. In the present section we discuss recent

developments of models applicable to liquids having more realistic interaction potentials

going beyond the simple hard-sphere type. For the Ramakrishnan and Yussouff model dis-

cussed in Section 2.1.3, of course, there is no speciﬁc limitation to the hard-sphere interac-

tion potential. Only the structural properties of the homogeneous liquid state in terms of the

direct correlation functions are required as input in solving the model equations and hence

the theory can, in principle, be applied to systems with any interaction potential. However,

the weighted-density-functional models described above require accurate knowledge of the

equation of state of the homogeneous liquid in order to obtain the correlations correspond-

ing to the inhomogeneous crystalline state. For the hard-sphere ﬂuid such information

is readily available from various standard integral-equation approaches. Extending the

density-functional model to systems with attractive potentials, e.g., Lennard-Jones inter-

action, requires special treatment of the long-range attractive forces between the particles.

The perturbation theory

We now discuss formulation of the density-functional theory for a system with a realistic

interaction potential that has a long-range attractive part. The treatment is analogous to the

earlier perturbative treatment of Weeks et al. (1971) (referred to above as the WCA theory)

for computing the thermodynamic properties of such systems in the homogeneous liquid

state. Let us consider a system interacting through a two-body potential that is character-

ized in terms of a reference potential and a perturbation, involving a small parameter κ,as

u(x

;κ) = u

) + κu

), (2.4.1)

representing the reference and the perturbative components of the two-body potential,

respectively. To formulate the density-functional theory of the inhomogeneous state of the

system with a realistic interaction potential u(x

) as described above, we ﬁrst construct

92 The freezing transition

the appropriate free-energy functional. A formal expression for the free energy is obtained

by starting from the exact deﬁnition of the two-point distribution function f

, x

) as

, x

) =ˆn(x

) ˆn(x

), (2.4.2)

where ˆn represents the microscopic one-particle density and the angular brackets refer to

the average over the equilibrium distribution. The two-point distribution function repre-

sents the probability of particles 1 and 2, respectively, being simultaneously at x

and x

The Boltzmann factor for obtaining the statistical average on the RHS of (2.4.2) is deter-

mined by the potential-energy part V of the Hamiltonian H .

The dependence of the total potential energy V on spatial coordinates is expressed in

terms of the two-body potential u(x

;κ) as follows:

(2)



ˆn(x

) ˆn(x

)u(x

;κ). (2.4.3)

From eqn. (2.4.3) it follows that the functional derivative of the partition function

Z =



exp[−β H ] (2.4.4)

with respect to the two-body potential u(x

) involves the product of two one-point den-

sity functions appearing between the angular brackets on the RHS of (2.4.2). Since the

Helmholtz free energy is given by

F =−k

T ln Z, (2.4.5)

the corresponding two-point function denoted by f

, x

;κ) is obtained formally in

terms of a functional derivative with respect to the two-body potential,

, x

;κ) =

δF[n

(x)]

δu(x

;κ)

. (2.4.6)

We integrate the relation (2.4.6) formally along κ = 0 to 1 to obtain the result

F[n

(x)]−F

(x)]=



dκ



, x

;κ)u

) ≡ F

, (2.4.7)

where F

[n(x)]is the Helmholtz free energy of the reference system having the interaction

potential u

. To lowest order in κ we obtain F



, x

), (2.4.8)

where f

, x

) denotes the two-particle distribution function for the system with inter-

action potential u

. Thus the free energy of the solid with interaction potential u(x

) is

obtained as

F[n

(x)]=F

(x)]+



, x

). (2.4.9)

2.4 Applications to other systems 93

In general an angularly averaged quantity

) for the two-point function f

, x

)

is deﬁned as

(x) =



d

4π



, x

+ x), (2.4.10)

d being the differential solid angle around x. Using the deﬁnition (2.4.10) for the angu-

larly averaged correlation function

f we obtain from (2.4.9) the following expression for

the free energy per particle of the inhomogeneous state for the system with interaction

potential u:

f [n

(x)]= f

(x)]+2πn



dr r

(r)u

(r). (2.4.11)

Thus both the free energy f

and the angularly averaged two-point distribution function

(r) of the reference system are required in order to construct the free-energy functional

for the system with interaction potential u(x

). Since the thermodynamic properties of the

hard-sphere system are well known, it becomes a natural choice for the reference system.

The interaction potential for the liquid is divided into a harshly repulsive part (representing

a hard core) and a long-range attractive part to be treated as a weak perturbation. The next

step in this calculation is therefore to choose a suitable description for the reference system

with interaction potential u

in terms of an equivalent hard-sphere system. The diameter of

the hard-sphere system is determined by setting suitable conditions, to be described below.

The reference system

For a short-range repulsive u

), the free-energy functional F

[n(x)] of the reference

system is obtained in terms of an equivalent hard-sphere system. The diameter d

of this

equivalent hard-sphere system is treated as an adjustable parameter in the theory and is

determined by applying a suitable criterion obtained from thermodynamic considerations.

To identify d

, the free energy of the reference system is written in terms of an expansion

around that for the hard-sphere system in powers of a blip function e(x

, x

= F



δF

(x)]

δe

, x

)

e(x

, x

) +···, (2.4.12)

where

e(x

, x

) = exp(−βu(x

)) (2.4.13)

is the Boltzmann factor for the interaction potential u(x

). The blip function is deﬁned as

e(x

, x

) = e

, x

) − e

, x

), (2.4.14)

namely as the difference between the Boltzmann factors for the reference potential u

and a

hard-sphere potential u

. If the range of the reference potential is comparable to the hard-

sphere diameter then the function e is nonzero only over a range of ξ d

with ξ<1,

whence the name blip function. Since the potential u is related to the Boltzmann factor e

94 The freezing transition

as −βu = ln e, it follows from (2.4.6) that the functional derivative of the Helmholtz free

energy with respect to e

, x

) is related to the two-point distribution function,

−β

δF[n

(x)]

δe(x

, x

)

= f

, x

βu

)

≡ y

, x

). (2.4.15)

On using the relation (2.4.15) and evaluating the angular part of the integral on the RHS of

(2.4.12) we obtain the result for the free energy as

(r)]=F

(r)]+2π V



dr r

˜y

(r)e(r) + O((e)

), (2.4.16)

where ˜y

(r) denotes the angular average of the hard-sphere function y

, x

) and is

obtained by averaging the latter over all orientations. The diameter d

of the equivalent

hard-sphere system with potential u

is adjusted so as to ensure that the ﬁrst-order term

in the expansion of eqn. (2.4.16) for the free energy vanishes. This is done by solving the

relation



∞

dr r

˜y

(r) =



∞

dr r

˜y

(r)e

−βu

, (2.4.17)

where d

is the diameter of the equivalent hard-sphere system. The discussion so far

is applicable to an equivalent hard-sphere system irrespective of whether the system is

homogeneous or not. For the isotropic liquid state translational invariance holds and the

angularly averaged quantity ˜y

(r) → g

(r), the uniform liquid-state radial distribu-

tion function for the reference system. From the solution of eqn. (2.4.17) using the pair

correlation function g

we obtain the corresponding value of the diameter d

of the equiv-

alent (uniform) hard-sphere system. For the above two key quantities f

and

(r) the

respective functional dependences on density are assumed to be the same as those of the

corresponding quantities for an equivalent hard-sphere system of radius d

The free energy

The free energy of the system with interaction potential u in the inhomogeneous solid state

is computed by making use of the above perturbation theory. We will discuss below two

approaches along these lines.

Model A The free energy f [n

(r)] per particle of the inhomogeneous system with interac-

tion potential u is obtained as an expansion around the corresponding uniform liquid state

(of density n

) constructed in terms of direct correlation functions of the liquid,

f [n

(r)]= f [n

]−

∞



n=2

β Nn!



dr ...



(n)

,...,r

)n

)...n

(2.4.18)

where c

(n)

is the n-particle direct correlation function of the liquid of density n

.Forthe

free energy f (n

) of the uniform state we substitute the corresponding limit of the RHS of

eqn. (2.4.11),

2.4 Applications to other systems 95

f [n

(r)]=f

]+2πn



dr r

(r)u

(r). (2.4.19)

We now choose the uniform reference system of density n

, in terms of an equivalent

hard-sphere system. The expansion (2.4.18) reduces in terms of the equivalent hard-sphere

system (as

(r) → g

(r))to

f [n

(r)]=f

]+2πn



dr r

(r;n

(r)

−

∞



n=2

β Nn!



dr ...



(n)

,...,r

)n

)...n

), (2.4.20)

Next we write the direct correlation function of the system in terms of that of the hard-

sphere system as c

(n)

= c

(n)

+ c

(n)

. Substituting this form of the direct correlation

function into the above equation gives

f [n(r)]=f

]−

∞



n=2

β Nn!



dr ...



(n)

,...,r

)n

)...n

)

+ 2πn



dr r

(r)u

(r)

−

∞



n=2

β Nn!



dr ...



c

(n)

,...,r

)n

)...n

(2.4.21)

The sum of the ﬁrst two terms on the RHS of eqn. (2.4.21) is equal to the inhomogeneous-

state free energy of the hard-sphere system, giving the result

f [n(r)]= f

]+2πn



dr r

(r)u

(r)

−

∞



n=2

β Nn!



dr ...



c

(n)

,...,r

)n

)...n

(2.4.22)

Let us now consider the example of the Lennard-Jones (LJ) interaction potential u(r) ≡

(r) which is deﬁned for two particles at a separation r in eqn. (1.2.117). u

is divided

into two parts, namely a hard-core repulsive part, u

, and an attractive potential, u

respectively deﬁned as

w(r ) + 

, for r <σ

0, for r >σ

(2.4.23)

96 The freezing transition

and

−

, for r <σ

w(r ), for r >σ

(2.4.24)

where σ

= 2

1/6

σ and w(r) is the RHS of eqn. (1.2.117). For the homogeneous liquid

state, its thermodynamic properties are obtained by treating the weak attraction u

as a

perturbation over a reference system having an interaction potential u

The free energy of the solid is determined by evaluating the RHS of eqn. (2.4.22).Asa

typical case the ﬁrst term on the RHS for the free energy of a hard-sphere system is com-

puted using the MWDA method. The second term is a mean-ﬁeld term (de Kuijper et al.,

1990) that depends on the pair correlation function g

(r) of the uniform hard-sphere ﬂuid

of diameter d

. The third term depends on the density function of the inhomogeneous

system and on the form of the c

(n)

. For simplicity we neglect the higher-order terms in

c

(n)

(n > 2). Estimations of c

(2)

are made for large and small distances with simple

approximations. For short distances both systems have a hard core and hence c

(2)

→ 0.

This ensures that the self-interaction does not inﬂuence the results. On the other hand, for

large r , e.g., beyond the potential-well minimum at σ

, the direct correlation functions are

approximately equal to the potentials and hence the difference is simply w(r). Over inter-

mediate distances of the order of the diameter of the equivalent hard sphere, c

(2)

(r) is dif-

ferent. The following approximation for c

(2)

has been used (Curtain and Ashcroft, 1986):

c

(2)

⎧

⎪

⎨

⎪

⎩

0, 0 < r < r

−β

, r

≤ r < 2

1/6

−βw(r), 2

1/6

≤ r,

(2.4.25)

where r

is a parameter related to the inter-particle spacing in the crystal and 

is the

depth of the potential well. The free energy of the stable solid is obtained by minimizing it

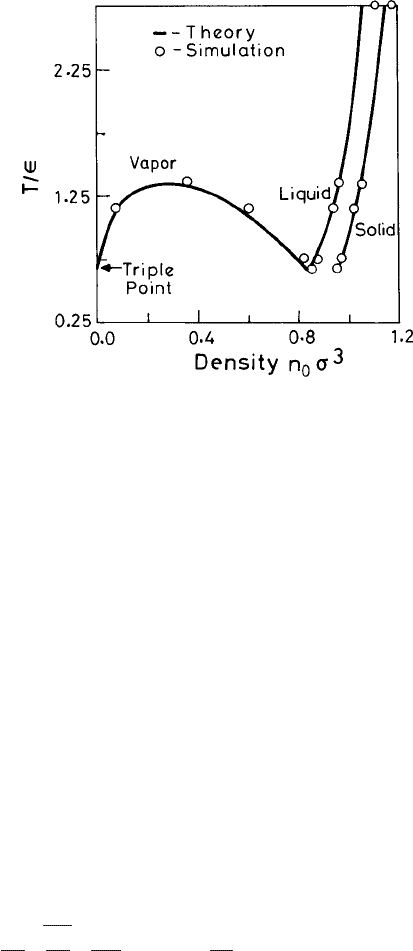
with respect to the variations of the parameters of the density function n(r).InFig. 2.5 the

temperature–density phase diagram of the Lennard-Jones system as calculated by applica-

tion of the present theory is shown. The Lindemann parameter L

remains nearly constant

at about 0.12–0.13 along the coexistence line.

Model B A somewhat different scheme for computing the free energy of the inhomoge-

neous state for systems with interaction potentials having a long-range attractive part has

been developed by Rascón et al. (1996). In this case the WCA approach is applied directly

to the inhomogeneous solid state and the free energy is computed from eqn. (2.4.11) in

terms of the reference state which itself is inhomogeneous. By using the hard-sphere

(r)

functional of the inhomogeneous solid state described above, a better estimation for the

mean-ﬁeld contribution to the free energy is obtained. The calculation of the corresponding

two-particle distribution function f

requires some special steps. An approximate eval-

uation of the two-point distribution function f

, x

) for the hard-sphere system as a

functional of the density n(x) for a Lennard-Jones interaction potential is done as follows.

2.4 Applications to other systems 97

Fig. 2.5 The phase diagram of a Lennard-Jones system obtained from model A is shown as a solid

line. The corresponding computer-simulation results are shown as circles. Reproduced from Curtain

and Ashcroft (1986).

 American Physical Society.

The two-point distribution function f

. Since the individual particles in a crystal are

sharply localized to their corresponding lattice sites, f

, x

) is approximated at the

simplest level as the product of the individual average single-particle densities,

, x

) = n

). (2.4.26)

The above approximation for f

, which is deﬁned in (2.4.2), amounts to neglecting the two-

point correlation in the crystal and is better applicable when the separation |x

−x

|is large.

To proceed further we need the inhomogeneous density function for the solid state. The

inhomogeneous density n

(x) for the hard-sphere system is expressed as a sum of Gaussian

proﬁles as deﬁned in (2.2.14) parametrized in terms of the WP α

(say). On substituting

this ansatz for n

(x) into the expression (2.4.26), and taking an angular average as deﬁned

in (2.4.10), we obtain an approximate expression

(r) for the two-point function:

(r) =



(r), (2.4.27)

where the functions f

(r) represent Gaussian peaks,

(r) =

4π

2π





exp



−

(r − R

)



, i = 2, 3,... (2.4.28)

Here R

is the radius of the ith shell around a lattice site chosen as the origin and w

is the

number of sites in the ith shell in the lattice. In deriving (2.4.28) we neglected contributions

involving exponential terms like e

−α

(r+R

)

, since for large α

values (correspond-

ing to the highly localized structures in the crystal) such factors are negligible at ﬁnite r

98 The freezing transition

values. Note that in (2.4.28) the angularly averaged two-point function is a function of the

hard-sphere packing fraction ϕ

for the equivalent hard-sphere system. The parameter α

in the expression for f

represents its functional dependence on the density function n

(x).

In deﬁnition (2.4.28) above we have not included the case i = 1 corresponding to the peak

at shortest r in

(r). The approximation used in obtaining (2.4.27) is valid at large r

but proves inadequate for including the correlations in the system at short length scales.

For short distance

(r) is parametrized using the known thermodynamic properties of the

corresponding hard-sphere solid as follows:

(r) =

/r) exp

−(α

/2)(r −r

)

, if r ≥ σ

0, otherwise.

(2.4.29)

The three parameters A

, α

, and r

are determined from the numerical solutions of three

coupled nonlinear equations obtained by imposing the following three constraints on

(r).

(a) The normalization of the angular-average two-point distribution function

(r)

over the ﬁrst shell is equal to the coordination number of that shell in the corresponding

crystal structure.

(b) The virial equation relating the pressure P of the system to the

(σ

) of the corre-

sponding hard-sphere crystal (σ

is the hard-sphere diameter) at contact applies.





calculated with

(21)

(r) should be the same as that computed with

In the scheme for obtaining

(r) for small r, outlined above, the pressure P at pack-

ing fraction ϕ

of the equivalent hard-sphere system is required as an input. The pressure

is obtained by computing the free energy of the solid with any of the standard density-

functional methods discussed above for hard-core systems. For an optimum value of the

width parameter α

=¯α in the hard-sphere density function, the free-energy functional

[n] of the equivalent hard-sphere system is a minimum. This minimum value corre-

sponds to the equilibrium free energy of the hard-sphere system of packing fraction ϕ.The

corresponding pressure P is determined from the numerical derivative with respect to the

density n

of the free energy F

at the minimum. Using this value of the pressure P as

well as the other constraints described above, the three constants in (2.4.29) are computed.

The two formulas, given by (2.4.28) and (2.4.29), respectively, lead ﬁnally to the angularly

averaged two-point distribution function,

(r) =

(r) +



i=2

(r). (2.4.30)

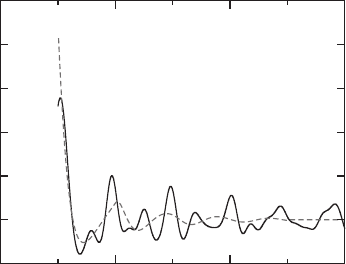
In Fig. 2.6 the angularly averaged correlation function

(r) of the hard-sphere f.c.c. solid

at packing fraction ϕ = 0.537, is plotted against the distance r scaled with the corre-

sponding hard-sphere radius. For the results presented here we have used the modiﬁed

weighted-density-functional approximation (MWDA) for computing the hard-sphere free

energy. It is important to note in this respect that the value of the equilibrium free energy

for the hard-sphere system considered above is different from F

of the reference

system. The latter is just a part of the total free energy of the LJ system. The DFT treat-

ment of the hard-sphere system (at packing fraction ϕ

for the equivalent system) with

2.4 Applications to other systems 99

0246

Fig. 2.6 The angularly averaged correlation function

(r) deﬁned in eqn. (2.4.10) vs. the radial

distance r/σ for a hard-sphere system at packing fraction 0.52. σ is the hard-sphere diameter.

density function characterized by Gaussian width α

as developed above is solely aimed at

determining the functional dependence of the free energy F

and the two-point distribution

function

(r) of the reference system on the inhomogeneous density function n

(x).

The total free energy for the inhomogeneous crystalline state is now obtained from

(2.4.11) for a chosen density n

and temperature T of the LJ system. This involves com-

puting the two parts f

and

in terms of the equivalent hard-sphere functionals obtained

above. The density function n

(x) is characterized by a width parameter denoted by α.The

equilibrium state corresponds to the minimum of the free energy f per particle obtained for

an optimum value of α. The hard-sphere system’s free energy for computing f

is obtained

here using the MWDA. The free energy of the Lennard-Jones crystal obtained theoretically

with the DFT approach described above is in very good agreement with corresponding

computer-simulation results (van der Hoef, 2000).

2.4.2 The solid–liquid interface

The density-functional theory of freezing outlined above has also been applied for mod-

eling a number of related physical systems. Among those of particular interest to our

present discussion is the study of the interface between coexisting solid and liquid phases

(Evans, 1990, 1992). The structure of the interface between the crystal and the liquid is

characterized by the sharp density peaks of the solid phase becoming gradually broader

with a corresponding decrease in height as the homogeneous-liquid side is approached.

The density peaks become more strongly overlapping, with the interface appearing like

a perturbed liquid and gradually smoothing into the homogeneous-liquid state of uni-

form density. The nature of the density proﬁles determines the overall width of the inter-

face. Following the general approach of the DFT of inhomogeneous solids, the density

distribution for the interface is determined from the minimization of the corresponding

excess grand potential ,

100 The freezing transition

 = F[n(x)]−μ



dx n(x) + PV, (2.4.31)

with the density n(x) approaching asymptotically the uniform-liquid density n

and the

solid-state density n

(x) on the two sides of the interface. Both phases are at the coexis-

tence values of the set of thermodynamic parameters (μ, P, T ).

The ﬁrst step in the formulation of a density-functional model for a theoretical descrip-

tion of the liquid–solid interface involves parametrization of the density n

(x) in the inter-

face region. Following the prescription (2.1.42) for the inhomogeneous density in the bulk

phase, we write down the density n

(x) in the interface region with the function

(x) = n

+ (n

− n

(z) +



(z)e

· x

, (2.4.32)

with the z axis being chosen perpendicular to the interface. In (2.4.32) the functions B

and B

are introduced to take into account the variation of the density n

(x) across the

interface. The criteria followed in constructing them are as follows.

(i) Each of the B

(for m = 0, 1, 2,...) is constructed so as to have values 0 and 1

corresponding to the bulk liquid and bulk solid phases, respectively.

(ii) The B

associated with the corresponding reciprocal wave vector K

must decay over

a shorter distance as the magnitude of K

increases. To maintain positive density, it is

necessary also that the larger K

is, the closer to the crystal the corresponding function

vanishes.

We consider here the ansatz for the B

as follows:

(z) =

⎧

⎪

⎨

⎪

⎩

1, z

> |z|,



1 + cos



z − z





0, z

< |z|.

⎫

⎪

⎬

⎪

⎭

, z

< |z| < z

, (2.4.33)

The quantity 

=|z

− z

| which represents the width of the density-variation range

corresponding to wave vector K

is parametrized in the form



=|z

− z







, 0 ≤ ν ≤ 1, K

≥ K

, (2.4.34)

with K

denoting the smallest nonzero RLV. 

is the width of the interface. Equations

(2.4.33) and (2.4.34) represent an interface slab geometry with the bulk solid phase in

|z| < z

, the bulk liquid phase in |z| > z

+ 

, and the interfacial region completely

conﬁned within the region z

< |z| < z

. This is shown schematically in Fig. 2.7.The

quantities n

and {n

} for a suitably chosen set of RLVs K

correspond to the coexist-

ing bulk liquid and solid phases, respectively. These are inputs for the test density function

(x) to be used in the free-energy calculation of the interface. In the parametrization of