Das Sh.P. Statistical Physics of Liquids at Freezing and Beyond

Подождите немного. Документ загружается.

2.1 The density-functional approach 71

Table 2.1 Comparison of the freezing parameters for hard spheres as obtained in

the Ramakrishnan–Yussouff theory, using the Percus–Yevick (PY) structure factor

(with and without the Verlet–Weiss (VW) correction) for the uniform liquid state,

and the simulation of Hoover and Ree (1968). From Haymet and Oxtoby (1986).

Structure factor Structure factor

(PY with VW) (PY without VW) Simulation

Average liquid density n

0.9460 0.9665 0.939–0.948

Average solid density n

1.037 1.033 1.036–1.045

Fractional density change η 0.0907 0.0690 0.0928–0.1129

Entropy change s/k

−1.047 −0.944 −1.16

(a) A suitable set of RLVs K

representing the crystal lattice into which the isotropic

liquid changes at the freezing point. Although the ansatz (2.1.42) for the inhomoge-

neous density can in principle involve an inﬁnite number of wave vectors, for practical

computations this series is terminated with a ﬁnite number of RLV values.

(b) The structural information of the uniform liquid state in terms of the c

. These quan-

tities are obtained as the Fourier transforms of the Ornstein–Zernike direct correlation

function c(r). In the present discussion we are restricting the computation to terms of

up to second order in density ﬂuctuations in the expression for the free energy and

hence only two-point direct correlation functions are involved.

The required input information of uniform liquid structure for obtaining the order parame-

ters of the freezing transition is in terms of the direct correlation function c(r). In principle

any simple liquid with available structural information (from experiment, computer simu-

lations or theoretical models) can therefore be studied with this model. In practice, how-

ever, the most widely investigated system is the hard-sphere ﬂuid. In their seminal paper

Ramakrishnan and Yussouff (1979) studied the hard-sphere system, restricting the set of

RLVs to two shells only. Subsequently Haymet and Oxtoby (1986) included up to 20 sets

of RLVs. We discuss this treatment in more detail in Appendix A2.2 and the results are

listed in Table A2.4. The scaled direct correlation functions c

of the hard-sphere system

are approximated with the Percus–Yevick (PY) (Percus and Yevick, 1958; Percus, 1962,

1964) structure factor with Verlet–Weiss (VW) corrections (described in Chapter 1). Fol-

lowing the scheme described above, this calculation tells us that the freezing transition

occurs at n

= 0.946 (σ is the hard-sphere diameter), to an f.c.c. solid with average

density n

= 1.03 and a fractional density change η = 0.09. These numbers are in good

agreement with the corresponding computer-simulation results as indicated in Table 2.1.

The entropy change (per particle) on freezing is obtained from the Clapeyron equation

(McQuarie, 2000),

s



−η

1 + η



. (2.1.46)

72 The freezing transition

The results with two different structural inputs of c

(with and without Verlet–Weiss correc-

tions to the structure factor) are listed in Table 2.1. The derivative dP/dT at the transition

point is directly computed from the corresponding equation of state, i.e., the empirical

Carnahan–Starling and the PY equation of state, respectively (described in Chapter 1).

The Ramakrishnan–Yussouff theory outlined above is a basic step towards our under-

standing of freezing phenomena. It provides a formulation of the ﬁrst-order phase transition

through identiﬁcation of the proper order parameters of the transformation process. The

density-functional formalism involved provides the thermodynamic properties of the inho-

mogeneous crystalline state in terms of those of the liquid state. However, in spite of the

usefulness of this model mentioned above, some severe approximations are made. The

most important is the truncation of the functional expansion of the excess free energy F

in terms of the density difference δn

(x) = n

(x) − n

. The particles in the crystal are

highly localized about the respective lattice sites and hence the average solid-state density

is strongly inhomogeneous, implying that the density difference δn is not small. Attempts

to include higher-order corrections in this series (Haymet, 1983) only make the situation

worse and result in poor predictions for the crystal–liquid coexistence conditions for the

hard-sphere system (Curtain, 1989). Furthermore, the density distributions in the crystal

as obtained from the calculation outlined above are much sharper than those found in sim-

ulation studies. The improvement of the theory of the freezing transition comes from the

weighted-density-functional theory for studying inhomogeneous ﬂuids. This is discussed

in the next section.

2.2 Weighted density functionals

The DFT for freezing involves studying the stability of the inhomogeneous solid by com-

paring its thermodynamic properties with those of the homogeneous liquid. In the previous

section we have discussed the calculation of the excess contribution to the free energy of

the crystal (over the so-called ideal-gas contribution for a noninteracting system) by retain-

ing low-order terms in a perturbation series. This excess part due to the interaction between

the particles is computed using the basic interaction potential between the particles as an

input. Improvement of the DFT has been achieved by making nonperturbative approxima-

tions for the excess free energy in terms of that of an equivalent system. The characteristics

of the coarse-grained system are determined from a weighted average of the inhomoge-

neous density of the original system. The corresponding weighting function(s) therefore

constitute a basic ingredient of this approach to studying inhomogeneous solids. It is

either self-consistently dependent on the density itself or chosen to be density-independent,

being determined from geometric considerations of the constituent particles. The density-

functional formulation with weighting is termed the weighted-density-functional theory.

The equivalent system is generally determined in terms of a local density, but schemes

with a position-independent density have also been formulated. The theory also requires

as an input a standard framework for computing the thermodynamic properties of the

equivalent low-density system. This makes a hard-sphere ﬂuid particularly suitable for

2.2 Weighted density functionals 73

developing such theories. In our treatment of the weighted-density-functional theories we

follow closely the developments due to Ashcroft and coworkers (Curtain and Ashcroft,

1985, 1986; Curtain, 1987; Denton and Ashcroft 1989) and also the fundamental-measure

theory (Rosenfeld, 1988, 1989; Rosenfeld et al., 1990) applicable to hard-sphere systems.

In the following we also discuss applications for systems whose interaction potentials have

a long-range attractive part in addition to the short-range repulsion.

In this approach the thermodynamic properties of the crystal are approximated with

a free-energy functional constructed using the following mapping. The free-energy den-

sity of the inhomogeneous system at a given point x

is the same as that of a homoge-

neous system, but evaluated at an auxiliary density ¯n

(x). The excess free energy F

obtained as



dx n

(x) f

WDA

[¯n

(x)]. (2.2.1)

The weighted density function ¯n

(x) is constructed by weighting the physical density



) over a relevant region around the point x



with a suitable weighting function w.

The dependence of ¯n on n should reﬂect the nature of the inhomogeneity present in a solid

phase and yet be general enough to be applicable to the different phases of the system.

For example, if the structured phase is a crystal, then the high degree of correlation in it

should be reﬂected in the corresponding coarse-grained system. On the other hand, for a

homogeneous liquid of constant density, the coarse-grained density should be the same

as the original density. This is achieved by making the functional dependence of ¯n

(x)

self-consistent and nonlocal:

¯n

(x) =





w(x − x



, ¯n

(x))n



). (2.2.2)

To satisfy the constraint that for a uniform system with density n

the weighted density

should also be n

, we have the normalization condition





w(x − x



, n

) = 1. (2.2.3)

Equations (2.2.1) and (2.2.2), which form the basis of the weighted-density approximation

(WDA), can in fact be justiﬁed from general considerations of the free-energy functionals.

We demonstrate this in Appendix A2.3.

The simplest functional dependence between the coarse-grained density ¯n

(x) and the

physical n

(x) is that provided by Tarazona (1984, 1985). Here w is assumed to be inde-

pendent of density. For a hard-sphere system, if the sphere of inﬂuence affecting the density

at a point is taken to be the hard-sphere diameter σ , then w has the form w(r ) = 3/(4πσ

)

for r ≤ σ and is zero otherwise. Other forms have also been studied in the literature

(Nordholm et al., 1980; Baus and Colot, 1985). As we will explain below, the weighting

74 The freezing transition

function can be computed in a self-consistent manner taking into account the correlations

present in the inhomogeneous solid. The basic idea behind the WDA is to take into account

how the short-ranged nonlocal effects in the interacting, inhomogeneous system (the crys-

tal) inﬂuence its thermodynamic properties. In the WDA the excess free energy of the

solid is interpreted as that of an effective liquid of much lower density than the average

solid density. It follows then in a natural way that the low-density liquid is what is required

to account for the correlations in the solid state. By choosing the weighting function in an

optimal way, an approximate re-summation of functional expansion (in terms of density)

of the exact excess free energy can be reached in the WDA.

In general the weighting function serves to smooth out the sharp density variations over

a spatial range by virtue of its being nonlocal in nature. Since the available information for

the inhomogeneous liquid is minimal, the weighting function is ﬁxed by using the known

properties of the uniform liquid state. w is chosen such that the known relation between the

two-point direct correlation function c

(2)

, x

) and the second functional derivative

in density of the excess free energy F

is strictly obeyed at the homogeneous limit of

(x) → n

(2)

, x

) =−β



WDA

[n]

δn(x

)δn(x

)



n(x)=n

. (2.2.4)

By deﬁnition of the weighted density function ¯n(x), the excess free energy is deﬁned as

WDA

(x)]=



dx n

(x) f

( ¯n

(x)), (2.2.5)

where f

) is the free-energy density for the homogeneous liquid of density n

.The

knowledge of a suitable function for f

) is a required input in formulating the weighted-

density-functional theory of the inhomogeneous liquid. Using the WDA form of the excess

free energy and evaluating the RHS of (2.2.4), one obtains (for the proof see Appendix

A2.3) the following relation between the direct correlation function c

(2)

(x, n

) of the

homogeneous liquid and the WDA weighting function w,

−β

−1

(2)

(x − x



) = 2 f



)w(x − x



)

+ n



)



w(x − x

)w(x

− x



)

+ n



)





w(x − x



− x



)

+ w



(x − x

)w(x

− x



)



. (2.2.6)

Since the direct correlation function c

(2)

(x − x



) of the homogeneous liquid is known,

the weighting function w is obtained from the solution of (2.2.6). Alternatively, the above

equation is Fourier-transformed to obtain

−β

−1

(2)

(k;n

) = 2 f



)w(k;n

) + n



(k;n

)

+ 2n



)w(k;n



(k;n

). (2.2.7)

2.2 Weighted density functionals 75

In the zero-wave-number limit, since the normalization condition (2.2.3) implies

w(0;n

) →1, the above relation reduces to the compressibility rule (Hansen and

McDonald, 1986)

−1

(2)

(0;n

) =−2 f



) − n



). (2.2.8)

Using c

(2)

(k;n

) as input, eqn. (2.2.7) is solved for w(k), which is then inverse Fourier-

transformed to obtain w(r). Hence the weighted density ¯n

(x) is also obtained from (2.2.2).

Let us consider the main features of the weighted-density-functional approach for the

thermodynamic description of the inhomogeneous crystalline state outlined above. With

the weighting function w determined from the solution of (2.2.6), a functional expansion of

−F

WDA

about a uniform reference state is guaranteed to be identical to the corresponding

expansion of −F

to second order in density differences. The higher-order terms in this

functional expression can also be obtained within the WDA by taking further functional

derivatives of −F

WDA

, since the relation

(m)

(k, 0,...;n

) =

∂

m−2

∂n

n−2

(2)

(k;n

) (2.2.9)

between c

(2)

(k;n

) and c

(n)

(k, k



,...;n

) is preserved for all m > 2. The WDA approxi-

mates the excess part of the free energy in a manner that is exact to lowest order in density

variations with arbitrarily large spatial ﬂuctuations typical of the crystalline state. It also

includes terms to all higher orders in a density expansion, since it provides the approxi-

mate expressions for three-point and all higher-point direct correlation functions using the

two-point functions of the homogeneous liquid.

2.2.1 The modiﬁed weighted-density approximation

The weighted-density-functional approach for computing the free energy of the inhomo-

geneous liquid is simpliﬁed to a large extent by further reﬁning the theory into a form

that has been termed the modiﬁed weighted-density-functional approximation (MWDA)

by Denton and Ashcroft (1989). In the MWDA the effective liquid in terms of which the

correlations in the solid are expressed has a constant density ˆn

rather than the ¯n

(x) of the

WDA. The excess free energy of the solid is now obtained in the form

= Nf

[ˆn

]. (2.2.10)

The density ˆn

of the equivalent liquid is obtained from the global average

ˆn





˜w(x − x



, ˆn

) (2.2.11)

in terms of a weighting function ˜w that is analogous to the corresponding quantity w of

the WDA. Similarly to in the case of the WDA, the basic MWDA equations (2.2.10) and

(2.2.11) can also be justiﬁed at a formal level. This is shown in Appendix A2.4.Wealso

76 The freezing transition

demonstrate in Appendix A2.4 that the weighting function ˜w(x) of the MWDA is obtained

in the form

˜w(x, x



, ˆn

) =−

2 f





−1

(2)

(x, x



) +

ˆn



( ˆn

)



, (2.2.12)

where f



represents the second derivative of the free-energy density f (n

) with respect

to the density. Now, on substituting this equation into the deﬁning relation for the basic

MWDA equation (2.2.11), we obtain the following self-consistent expression for the den-

sity ˆn

ˆn

=−

2 f





ˆn



( ˆn

) + β

−1



dx n

(x)





)



(2)

(x, x



;ˆn

)



. (2.2.13)

The above self-consistent relation is solved for a chosen density function n

(x) to obtain

ˆn

. The only input required is the two-point direct correlation function c

(2)

for the uniform

liquid state. The free energy of the inhomogeneous solid is obtained in terms of the relation

(2.2.10).

The necessary steps required to compute the free energy of the inhomogeneous solid in

the WDA and in the MWDA are similar. The following inputs are necessary in both cases.

(a) A suitable prescription for the inhomogeneous density function n

(x) of the solid state.

(b) The direct correlation function c

(2)

(r) of the homogeneous liquid.

) for the homogeneous liquid of density n

Parametrization of the inhomogeneous density function constitutes the basic step in the

DFT model. We consider in the next section a standard choice of the inhomogeneous

density function n

(x) for the crystalline state.

2.2.2 Gaussian density proﬁles

In the stable crystalline phase for standard materials the root-mean-square displacements

of the atoms are only a small fraction of the nearest-neighbor separations. The Hamiltonian

for the crystal reduces to a harmonic expansion in terms of displacement from the lattice

sites. The corresponding excitations of the dynamic crystalline state are the phonons. The

inhomogeneous density function is suitably approximated as a sum of Gaussians,

(x) =





3/2



−α(x−R)

, (2.2.14)

where the parameter α is the inverse width of the Gaussian. The α =0 limit corresponds

to the uniform liquid with inﬁnitely wide Gaussian proﬁles and increasing values of α

correspond to more strongly localized density proﬁles. The Lindemann parameter L

asso-

ciated with the melting of a solid is deﬁned as the ratio of the root-mean-square displace-

ment of an atom of the solid from its lattice site to the nearest-neighbor distance in the

crystal at coexistence. The width parameter α is inversely proportional to L

= 3/(αa

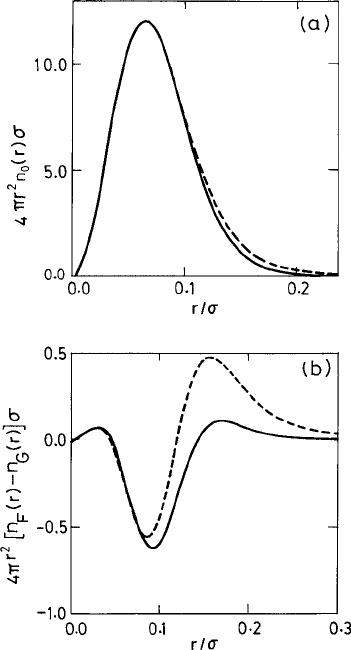
2.2 Weighted density functionals 77

Fig. 2.2 (a) The radial density function 4πr

(r)σ for the Lennard-Jones particles at the freezing

point measured from a lattice site with r in the (100) and (111) directions (solid line) and in the (110)

direction (dashed line). The deviations of n

(r) from the Gaussian form n

is shown in (b) by the

corresponding curves. Adapted from Laird et al. (1987).

 American Institute of Physics.

where a = (4/n

)

1/3

is the lattice constant of the f.c.c. lattice. For the hard-sphere system

the single-particle density function is also described quite accurately in terms of the above

expression of the sum of Gaussian proﬁles. The suitability of the Gaussian density approx-

imation is further clariﬁed in Fig. 2.2, where the radial density function 4πr

(r)σ for a

system of particles interacting through the Lennard-Jones (L-J) potential is shown (see eqn.

(1.2.117) for the deﬁnition of the L-J potential). Figure 2.2 clearly shows that the density

proﬁle in the crystalline phase is well approximated in the Gaussian form.

The single-parameter formulation (2.2.14) of the density function is simply related to the

earlier expansion (2.1.42) in terms of RLVs. To see this, let us consider the Ramakrishnan–

Yussouff parametrization of the inhomogeneous density function n

(x),

Note that this expression is slightly different from that of (2.1.42).

78 The freezing transition

(x) = n



1 +

∞



m=1

· x



. (2.2.15)

By Fourier transforming the density function as given by both of the above two expressions,

(2.2.14) and (2.2.15), we obtain for n

)

= n

)





3/2





dx e

−α(x−R)

−K

· x

. (2.2.16)

On completing the square in the exponential and evaluating the Gaussian integral we obtain

the result

= exp



−K

/(4α)

, (2.2.17)

which links the order parameters

in terms of the width parameter α. The parametriza-

tion (2.2.14) for the density function is closely associated with the Debye model (McQuarie,

2000) of the crystal and is further discussed in Appendix A2.5. The parametrization of

the density in terms of the Gaussian proﬁles has been particularly useful for describing

the inhomogeneous solid, as we will demonstrate in a number of applications in

this book.

2.2.3 The hard-sphere system

In the weighted-density-functional theories (both WDA and MWDA) the free energy of the

solid is obtained in terms of an effective liquid of much lower density. Accurate knowledge

of the thermodynamic properties (equilibrium correlation functions) of the homogeneous

liquid is therefore essential for computing those properties for the solid state. The hard-

sphere ﬂuid satisﬁes the criteria very well since the various integral-equation theories

provide a very good account of the correlations in a hard-sphere system at low densities.

The self-consistent equations (2.2.7) and (2.2.13) of the WDA (Curtain and Ashcroft, 1985,

1986) and the MWDA (Denton and Ashcroft, 1989), respectively, are solved, using the

direct correlation function c(r) of the Percus–Yevick (PY) solution (see Chapter 1)for

the hard-sphere ﬂuid. The the excess-free-energy function f

is obtained by computing the

pressure P of the system from the corresponding equation of state which relates P to

the density n

of the liquid. For the PY solution this is given by

β P

1 + ϕ +ϕ

(1 − ϕ)

. (2.2.18)

ϕ = πn

/6 is the packing fraction of the ﬂuid and σ is the hard-sphere diameter. The

excess free energy f

is computed by integrating the equation

2.2 Weighted density functionals 79

β P/n

= 1 + ϕ

∂β f

∂ϕ

, (2.2.19)

leading to the result



(1 − ϕ)

− 1



− ln(1 −ϕ). (2.2.20)

The calculation of the thermodynamic properties of the inhomogeneous solid using the

weighted-density-functional theory therefore involves the following basic steps.

Calculation of the free energy of the solid

For a chosen density function, determined by the width parameter α, the WDA (MWDA)

free energy is calculated by obtaining the corresponding weight function w ( ˜w). Hence we

obtain the density for the corresponding equivalent liquid ¯n

(ˆn

)oftheWDA(MWDA).

The free energy thus computed is then minimized with respect to the parameter α of the

test density function to obtain the density distribution for the thermodynamic state. By

comparing the free energies of the liquid and solid states, the thermodynamic parameters

for the freezing point are obtained. To determine the coexisting densities of the two phases,

the respective grand potentials () are equated for two states having the same chemical

potential (μ).

The thermodynamically stable inhomogeneous structure for the crystalline state is iden-

tiﬁed from the minimum of the total free energy F = F

+ F

. At a given density (below

the freezing point) this free energy corresponds to a certain value of the width parameter α

lying between the homogeneous-liquid limit of α → 0 and the strong-localization case of

α →∞.

The key aspect of the weighted-density-functional approach for studying inhomoge-

neous solids can be understood as follows. For the very localized density proﬁles charac-

teristic of the crystal, the expression (2.1.25) for the ideal-gas part F

of the free energy

reduces to the form

β F

(α)/N =−

+ ln





(

)

3/2



(2.2.21)

corresponding to the large-α limit. It is monotonically increasing with α. On the other

hand, the excess or interaction part of the free energy evaluated with the MWDA or the

WDA approximation monotonically decreases, favoring strong localization of the particles

around the lattice sites. Physically this implies that with increasing localization each parti-

cle feels the effects of its neighbor to a lesser extent. This is very different from the case of

a high-density liquid in which the particles are strongly interacting. It is therefore possible

to map the interaction contribution to the free energy of the solid to that of a uniform liquid

of much lower density. The solid-state correlations are modeled by an effective liquid of

much lower density.

80 The freezing transition

Let us now consider the explicit computation of the excess free energy of the hard-sphere

crystal in the WDA and MWDA schemes.

A. In the WDA the equation (2.2.7) is solved to obtain w(k), which is then Fourier-

transformed to obtain w(r). The density ¯n

(x) of the effective liquid is obtained for

a given choice of the density function n

(x) (which is ﬁxed by a corresponding value

of α). The excess free energy of the liquid is obtained by computing locally the function

( ¯n

(x)).

B. In the MWDA the density ˆn

for the equivalent liquid is obtained by solving self-

consistently the single equation (2.2.13) for a chosen value of the width parameter α.

The excess free energy of the solid is then calculated as f

( ˆn

Clearly the WDA calculation is computationally more cumbersome since calculation of

the weight function w requires solving a differential equation. This is much simpler in

the case of the MWDA, for which the density ˆn

is obtained at much less computational

effort. Furthermore, unlike in the MWDA, in the WDA the excess free energy f

has to

be computed locally and then integrated over the system.

In order to illustrate the weighted-density-functional approximation it will be useful to

discuss the details of the calculation in the simplest case, i.e., the MWDA model for the

freezing transition in a hard-sphere system. For the f.c.c. solid into which the liquid freezes,

the lattice constant is given by a = (4/n

)

1/3

. Self-consistent solution of (2.2.13) gives the

equivalent liquid density ˆn

for a given value of α. The free-energy contributions corre-

sponding to the ideal and excess parts are computed as functions of α, and the minimum of

the total free energy at the optimum parameter value α ≈ 127 corresponds to the equilib-

rium density distribution. The corresponding weight function ˜w of the MWDA is obtained

by using the self-consistent solution ˆn

on the RHS of (2.2.12). The curves for the liquid-

and solid-state free energies (see Fig. 2.3) cross at an intermediate density that marks the

phase transition of the system from a homogeneous liquid state to a more localized density

distribution with f.c.c. crystal structure. The free energy of the liquid state shown in Fig. 2.3

is computed from the Carnahan–Starling equation of state (see Chapter 1), which provides

an accurate description of the thermodynamics near freezing point. A higher degree of

mass localization (higher α values) occurs with increasing average density n

Determination of the densities of the coexisting phases

The densities of the coexisting phases in the MWDA are determined by a common-tangent

construction to ensure that the appropriate thermodynamic conditions are satisﬁed. The

chemical potential and the thermodynamic potential of the solid phase are computed using

the relations

μ(n

) =

∂ f (n

)

∂n

(n

) = F(n

) − μ(n

. (2.2.22)

The corresponding quantities for the uniform liquid state are obtained using the Carnahan–

Starling equation of state. The coexisting solid and liquid densities satisfy simultaneously