Das Sh.P. Statistical Physics of Liquids at Freezing and Beyond

Подождите немного. Документ загружается.

5.1 Conservation laws and dissipation 211

in the pressure P in terms of the density ﬂuctuations (ignoring any coupling to the energy

ﬂuctuations for simplicity):

δ P =



∂ P

∂ρ



δρ = c

δρ , (5.1.43)

where c

turns out to be the speed of sound in the ﬂuid. Using the relations (1.2.52) and

(1.2.70), the thermodynamic derivative on the RHS of (5.1.43) can be expressed in terms

of the static structure factor S(0) as c

= 1/(βmS(0)). The dissipation matrix L

relates

to the viscosities,

(

)

∇

+ η

∇

, (5.1.44)

and h = e + P is the enthalpy density with e and P the energy density and pressure at

equilibrium, respectively. Conventional hydrodynamics generally refers to the region of

low frequency ω and small wave number k so that ωτ

 1 and kl  1, where τ

is the

mean time between collisions and l is the mean free path. In eqns. (5.1.41) and (5.1.42) the

dissipative terms representing transport in the nonuniform state are only up to linear order

in gradients of the local thermodynamic ﬁelds and therefore only slow processes occurring

over long length and time scales are considered. The transport coefﬁcients appearing in the

hydrodynamic equations are constants and are treated as known inputs. Equations (5.1.40)

and (5.1.41) will be the primary focus in the subsequent chapters on our discussion of the

dynamics of a one-component ﬂuid.

5.1.4 Tagged-particle dynamics

The dynamics of a single particle moving in a surrounding ﬂuid can be described in terms

of the density of the single particle ˆn

(r, t), which is deﬁned by eqn. (1.3.27) in Chap-

ter 1. The average ˆn

 of the tagged-particle density is obtained in eqn. (1.3.28) and is of

O(1/V ). It goes to zero in the thermodynamic limit V →∞. The velocity of this particle

is v

. In the very-long-time limit the behavior of the tagged-particle correlation is expected

to be diffusive. In order to demonstrate this we note that tagged-particle density n

(x, t) is

a conserved density and its integral over the whole volume is ﬁxed at unity. By taking a

time derivative of eqn. (1.3.27) we obtain the following balance equation:

∂ ˆn

∂t

+∇·

= 0, (5.1.45)

where the current

= v

δ(x − r

). The above equation is closed by assuming for long

times the constitutive relation between the averaged macroscopic particle current v and the

density n

. This phenomenological relation linking the macroscopic particle current with

the gradient of the tagged-particle density is given by Fick’s law,

(x, t) =−D

∇n

(x, t), (5.1.46)

212 Dynamics of collective modes

where the constant of proportionality D

is a kinetic coefﬁcient. Substituting the closing

relation (5.1.46) into the coarse-grained version of eqn. (5.1.45), now leads to a closed

equation for the average tagged-particle density n

(r, t):

∂n

∂t

− D

∇

= 0. (5.1.47)

The above diffusive equation represents the hydrodynamic behavior of the single-particle

motion in terms of the diffusive process with the phenomenological constant D

5.1.5 Two-component systems

The equation of the hydrodynamics for the one-component system is easily extended to a

two-component mixture. In this case the densities of the individual species are separately

conserved quantities. The set of slow variables therefore consists of the two partial densities

(x), s = 1, 2, and the total momentum density g(x). The mass densities are deﬁned

microscopically as

ˆρ

(x) = m



δ(x − r

(t)), (5.1.48)

where m

and r

(t) denote the mass and the position of the αth particle of the sth species,

respectively. The momentum densities g

for the two species are represented similarly as

(x) =



δ(x − r

(t)), s = 1, 2, (5.1.49)

where p

is the momentum of the αth particle of species s (s = 1 or 2) and N

is the

number of particles of the sth species in the mixture. N is the total number of particles

in the system, N = N

+ N

. The relative abundances of the two species are given by

= N

/N for s = 1, 2, such that x

+ x

= 1. The number of particles of species s per

unit volume V is deﬁned as n

= N

/V with n

= N/V = n

. The average mass

density ρ

is obtained as ρ

= m

+ m

. The total momentum density g = g

+ g

in a binary mixture is a conserved property and hence a hydrodynamic variable. The total

density

ˆρ(x, t) =ˆρ

(x, t) +ˆρ

(x, t) (5.1.50)

satisﬁes the continuity equation as in the one-component system. Since the individual den-

sities ρ

and ρ

are separately conserved in the binary system, in addition to the total

density there is an extra conserved quantity. This is the concentration variable ˆc deﬁned as

5.1 Conservation laws and dissipation 213

ˆc(x, t) = x

ˆρ

(x, t) − x

ˆρ

(x, t). (5.1.51)

For simplicity we avoid inclusion of the energy variable in the set here. The set of micro-

scopic equations for the dynamics now includes an additional equation for ˆc. The equation

for the momentum density is now modiﬁed from that corresponding to the one-component

system,

∂ ˆρ

∂t

+∇·

g = 0, (5.1.52)

∂ ˆg

∂t



∇

ˆσ

= 0, (5.1.53)

with the corresponding currents being given by

g(r) =



s=1



δ(r − r

), (5.1.54)

ˆσ

(r) =



s=1

⎡

⎣



δ(r − r

) +

















⎤

⎦

, (5.1.55)

where the sum over α

and β



excludes the case α

= β



. We have used the deﬁnitions of

the following quantities in terms of the force F



acting on the particle at r

due to the

particle at r









dwδ(r − r

+ wr



), (5.1.56)



αβ

= (r



· F



)ˆr



ˆr



. (5.1.57)

The vector r



= r

−r



and ˆr



is the ith component of the unit vector



.Note

that 



= 



and the quantity 



is also symmetric under exchange of {α

,β



}

as well as {i, j }. The microscopic stress tensor is symmetric, ˆσ

=ˆσ

, as in the case of

the one-component liquid. The microscopic balance equation satisﬁed by the concentration

variable c(r, t ) is obtained in the form

∂ ˆc

∂t

+∇·

= 0, (5.1.58)

where the current

is obtained as

= x

− x

. (5.1.59)

Considering as above the currents from the frame moving with the local velocity v(x, t),

we obtain that the average current is given by

(x, t)

= c(x, t)v(x, t ) (5.1.60)

214 Dynamics of collective modes

and the corresponding reversible equation for the variable c(r, t) is obtained in the form

∂c(r, t )

∂t

+∇· [v(r, t)c(r, t)]=0. (5.1.61)

The dissipative part of the concentration equation is computed by a similar procedure to

that above. The local equilibrium distribution (5.1.15) now involves an extra coupling to

the concentration variable,

(

, t)

= Q

−1

exp

−



dr β(r, t)



ˆe(r) − v(r, t) · ˆg(r)

−



(r, t) +

(r, t) −

(r, t)



ˆρ(r) − μ(r, t) ˆc(r)

4

(5.1.62)

where μ = μ

− μ

is the difference between the chemical potentials of the

two species. In the one-component limit the above expression for the distribution function

reduces to the form (5.1.15). The corresponding part of the dissipative current is obtained

for a positive deﬁnite rate of entropy production as

(x, t)

=−γ

∇μ, (5.1.63)

where γ

is a phenomenological kinetic coefﬁcient introduced to include the dissipative

effects. The equations for the total density ρ(x, t ) and the total momentum density g(x, t)

are respectively similar to eqns. (5.1.40) and (5.1.41) for the one-component case. By

exploiting the thermodynamic relation of the differential for the pressure P and that for

the chemical potential μ,

δ P =



∂ P

∂ρ



δρ +



∂ P

∂c



δc, (5.1.64)

δμ =



∂μ

∂ρ



δρ +



∂μ

∂c



δc, (5.1.65)

in terms of the concentration ﬂuctuation δc and density ﬂuctuation δρ a closed set of dis-

sipative equations of motion for the slow variables in the binary mixture is obtained. The

equation of motion for c(r, t ) is obtained in the form

∂c(r, t )

∂t

+∇· [v(r, t)c(r, t)]−D

∇

c(r, t) − D



∇

ρ(r, t) = 0, (5.1.66)

where

= γ



∂μ

∂c



, (5.1.67)



= γ



∂μ

∂ρ



(5.1.68)

are related to the inter-diffusion constant.

5.2 Hydrodynamic correlation functions 215

5.2 Hydrodynamic correlation functions

In the previous section we obtained the deterministic equations for the time evolution

of the coarse-grained densities ψ

(r, t) ≡{ρ,g, e}. These dissipative equations involve

transport coefﬁcients that act as material-dependent inputs in the theory. The correspond-

ing time correlation functions

(r, t)ψ



, t



)

of the coarse-grained densities (e.g., the

autocorrelation of the density variable ρ(k, t)) can be computed with the understanding

that the angular brackets now imply the average over the initial conditions. This averaging

is generally done in terms of the probability of the initial distribution of the local densities

and is determined by the local equilibrium distribution. The resulting correlation functions

correspond to long distances and times (or, equivalently, small wave numbers and frequen-

cies) and are termed the hydrodynamic correlation functions. They involve the transport

coefﬁcients representing the dissipation. Turning the argument the other way around, the

correlation functions can be used to deﬁne the transport coefﬁcients. Furthermore, if we

work with the plausible hypothesis that these hydrodynamic correlation functions are iden-

tical to the microscopic correlation functions in the proper limit, then this leads us to a

microscopic deﬁnition of the transport coefﬁcients in terms of equilibrium correlation func-

tions. This is also in agreement with the fact that the linear response of the system to an

external perturbation is related to the equilibrium correlation functions. In the following

we will obtain such hydrodynamic correlation functions for the dissipative equations for

the one-component system discussed in the previous section. This will ﬁnally lead us to

microscopic expressions for the transport coefﬁcients in terms of equilibrium correlation

functions.

We begin with eqns. (5.1.40) and (5.1.41) for the density ρ and momentum density g,

respectively. For simplicity and keeping in mind our primary focus in this book, we ignore

coupling to the energy ﬂuctuations. We also restrict our consideration to the linear form of

the equations of motion for ρ and g

. On multiplying both eqn. (5.1.40) and eqn. (5.1.41)

by ρ(x



, 0) and taking the thermal average, we obtain, respectively,

∂

∂t

ρρ

(k, t) +



(k, t) = 0, (5.2.1)

∂

∂t

(k, t) + ic

ρρ

(k, t) −



(k, t) = 0, (5.2.2)

where the spatial dependence has been Fourier-transformed with wave vector k. On multi-

plying eqn. (5.2.2) by k

and summing over i, we obtain, using eqns. (5.2.1), (1.3.25), and

(5.1.44), the following equation for the density correlation function:



∂

∂t

+ 

∂

∂t

+ c



ρρ

(k, t) = 0. (5.2.3)

The above equation represents the damped sound waves of speed c

in the ﬂuid. The

damping or sound attenuation is given by the kinetic viscosity 

= D

/ρ

, where

216 Dynamics of collective modes

= ζ

+ 4η

/3 is the longitudinal viscosity of the ﬂuid. By taking a Laplace trans-

form, as deﬁned in eqn. (1.3.73),ofeqn. (5.2.3) and using the general result (1.3.8) for the

intial time derivative of the density–density correlation function, we obtain G

ρρ

(q, z) in

the form of a continued fraction,

ρρ

(k, z) =−G

ρρ

(k, t = 0)



z −

z + i 



−1

, (5.2.4)

where G

ρρ

(k, t = 0) = β

−1

χ is the equal-time density–density correlation function. Next,

on multiplying eqn. (5.1.41) by g



, 0) and taking the thermal average, we obtain for the

time evolution of the current correlation function

∂

∂t

(k, t) + c

ρg

(k, t) −



(k, t) = 0. (5.2.5)

Now we choose both of the components i and j in the direction transverse to the vector k

such that

= 0. Using eqns. (1.3.25) and (5.1.44), we obtain the following

equation for the transverse-current correlation function G

(q, t):

∂

∂t

(k, t) + ν

(k, t) = 0, (5.2.6)

with the kinetic viscosity ν

= η

/ρ

. The Laplace transform G

(k, z) of the transverse-

current correlation function is obtained from the above equation as

(k, z) =

(t = 0)

z + ik

, (5.2.7)

where the equal-time correlation G

(t = 0) = ρ

−1

. The above relation leads to a useful

expression for the shear viscosity,

lim

ω→0

lim

k→0

(k,ω). (5.2.8)

As a consequence of the continuity equation (5.1.33), the longitudinal-current correlation

function G

(k,ω)is related to the density correlation function through the relation

ρρ

(k,ω) = k

(k,ω). (5.2.9)

Using this and the expression (5.2.4) for the density correlation function, it is straight-

forward to reach the following limiting expression for the longitudinal viscosity, which is

similar to eqn. (5.2.8) for the shear viscosity:



+ ζ

lim

ω→0

lim

k→0

(k,ω), (5.2.10)

wherewehaveusedtherelationχ

ρρ

(k) =mn

S(k) and in the small-k limit

1/(βmS(0)) = c

5.2 Hydrodynamic correlation functions 217

5.2.1 Self-diffusion

In an identical manner, by averaging over the initial distribution, we obtain from the

coarse-grained equation (5.1.47) for the tagged-particle density n

(r, t) the equation for

the corresponding hydrodynamic correlation function G

(r, t). For long times and long

distances it satisﬁes the diffusion equation

∂G

∂t

− D

∇

= 0. (5.2.11)

The solution for G

(r, t) is easily obtained in the form

(r, t) =

(4π D

3/2

exp



−



, (5.2.12)

where the normalization constant has been chosen to satisfy the condition (1.3.30).The

corresponding solution for the Fourier transform of G

(r, t) is obtained as

(k, t) = exp



−D

. (5.2.13)

The frequency wave-vector transform of G

(r, t) is denoted as S

(k,ω) and has the

Lorentzian form

(k,ω) =

+ (D

)

. (5.2.14)

(k,ω)follows the sum rule



+∞

−∞

dω

2π

(k,ω) = 1 (5.2.15)

to ensure that F

(k, t = 0) = 1. Finally, the diffusion coefﬁcient D

for the decay of the

tagged-particle correlation is obtained from the relation

lim

ω→0

lim

k→0

(k,ω). (5.2.16)

In a similar manner we also reach an equation for the autocorrelation of the concentration

variable c(r, t), which is an extra conserved density for a two-component system. The

linearized equation of motion in this case is obtained by an averaging of eqn. (5.1.66),



∂

∂t

+ D

c(k, t)



(k, t) + D



ρc

(k, t) = 0. (5.2.17)

If the coupling with the density ﬂuctuations is ignored then the Laplace transform of the

concentration correlation is obtained in the simple diffusive-pole form as in eqn. (5.2.7).

The corresponding inter-diffusion constant D

is given by an expression similar to (5.2.16),

lim

ω→0

lim

k→0

(k,ω), (5.2.18)

where χ

is the equal-time correlation of the concentration variable c.

218 Dynamics of collective modes

5.2.2 Transport coefﬁcients

In the above discussion of the dynamics of the ﬂuid in terms of the dissipative equations we

have considered the transport coefﬁcients such as the viscosity and thermal conductivity.

The latter were introduced as constants that deﬁned the dissipative parts of the correspond-

ing currents representing a microscopic conservation law for the ﬂuid. While the basic

form of the hydrodynamic equations is the same for different ﬂuids, the actual values of

the transport coefﬁcients appearing in these equations depend on the material properties

of the corresponding ﬂuid. A basic goal for the theory, therefore, is to obtain the transport

coefﬁcients in terms of the characteristic microscopic parameters for the system. As we

have seen above, the linear response of a nonequilibrium system to an external perturba-

tion is related to the corresponding equilibrium correlation of spontaneous ﬂuctuations.

Indeed, the linear transport coefﬁcients appearing in the hydrodynamic equations can be

obtained in terms of the equilibrium time correlation functions (see eqn. (1.3.3)). In eqns.

(5.2.8), (5.2.10), and (5.2.16), respectively, we have expressed the shear, longitudinal, and

self-diffusion coefﬁcients of a one-component ﬂuid. We demonstrate below that these rela-

tions reduce to integrals over time correlation functions of projected currents, which are

termed the Green–Kubo relations for the transport coefﬁcients.

Green–Kubo relations

We start from the expression (5.2.8) for the shear viscosity to obtain

lim

ω→0

lim

k→0



(k,ω)

lim

ω→0

lim

k→0



+∞

−∞

d(t − t



iω(t−t



)

∂

∂t ∂t



(k, t − t



). (5.2.19)

The above steps follow directly from partially integrating twice. Now, using the deﬁnition

for the Fourier transform of the tagged-particle correlation function,

(k, t − t



) =

g

(k, t)g

(−k, t



), (5.2.20)

in eqn. (5.2.19), we obtain

lim

ω→0

lim

k→0



+∞

−∞

d(t − t



iω(t−t



)

∂g

(k, t)

∂t

∂g

(−k, t



)

∂t



The spatial Fourier transform of the balance equation for the momentum density g in terms

of the stress tensor is

∂g

(k, t)

∂t

= k

(k, t). (5.2.21)

5.2 Hydrodynamic correlation functions 219

Now, choosing the direction of k in the z direction, we obtain the transverse component

along the x direction from the RHS of (5.2.21) as

lim

ω→0

lim

k→0



+∞

−∞

d(t − t



iω(t−t



)

σ

(k, t)σ

(−k, t



). (5.2.22)

Since the equilibrium correlation function of the stress on the RHS above is dependent

only on the difference of the two times it is an even function of time. Hence we obtain

= lim

k→0



∞

dtσ

(k, t)σ

(−k, 0). (5.2.23)

In an identical way, starting from the relation (5.2.10), we obtain for the longitudinal

viscosity the corresponding relation



= lim

k→0



∞

dtσ

(k, t)σ

(−k, 0).

However, the diagonal element of σ

(k, t) is nonzero in the long-time limit. As already

deﬁned in eqn. (A5.1.25), the nonzero average value of the diagonal element is the hydro-

dynamic pressure P in the ﬂuid,

lim

k→0

(k, t) = PV. (5.2.24)

This makes the integral on the RHS of eqn. (5.2.24) diverging. This is rectiﬁed by subtract-

ing out the constant part from the diagonal element of the stress, thereby obtaining ﬁnite

transport coefﬁcients in terms of the correlation of stress ﬂuctuations:



= lim

k→0



∞

dt{σ

(k, t) − PV}{σ

(−k, 0) − PV}. (5.2.25)

The above examples for the Green–Kubo relation are easily extended to the self-diffusion

coefﬁcient D

. We start from the expression (5.2.16) to obtain, in an identical manner to

that above,

lim

ω→0

lim

k→0



(k,ω)

lim

ω→0

lim

k→0



+∞

−∞

d(t − t



iω(t−t



)

∂n

(k, t)

∂t

∂n

(−k, t



)

∂t



lim

k→0



+∞

−∞

d(t − t



)

v

(k, t)v

(−k, t



). (5.2.26)

In the small-k limit the equilibrium correlation of the velocity of the αth particle is diagonal

and is proportional to δ

. Using this in eqn. (5.2.26),

220 Dynamics of collective modes



+∞

d(t)ϕ

(t).

(t) =v(t) · v(0) represents the correlation of the single-particle velocities at two dif-

ferent times. The self-diffusion coefﬁcient is expressed as an integral over the equilibrium

time correlation function of tagged-particle velocities at two different times. Note that the

hydrodynamic form (5.2.13) of the tagged-particle correlation is then identical to what

is obtained for the microscopic quantity in eqn. (1.3.57), provided that we identify D

from the Green–Kubo relation (5.2.27). For a purely Gaussian system the tagged-particle

correlation F

(k, t) is entirely determined by D

or the current correlation function ϕ

(t).

Using the relation (1.3.56), it also follows that the mean-square displacement of the

tagged particle is given by

r

(t)=6D

t, (5.2.27)

which is termed the Einstein relation. In a dense liquid the tagged particle is caught in

a cage formed by its neighbors and the rattling motion of the particle in the cage causes

a negative tail for the velocity correlation function. Eventually, over structural-relaxation

times, the cage breaks and the correlation ϕ

(t) decays to zero. The relation (5.2.27) shows

that the negative tail results in a fall of the self-diffusion coefﬁcient D

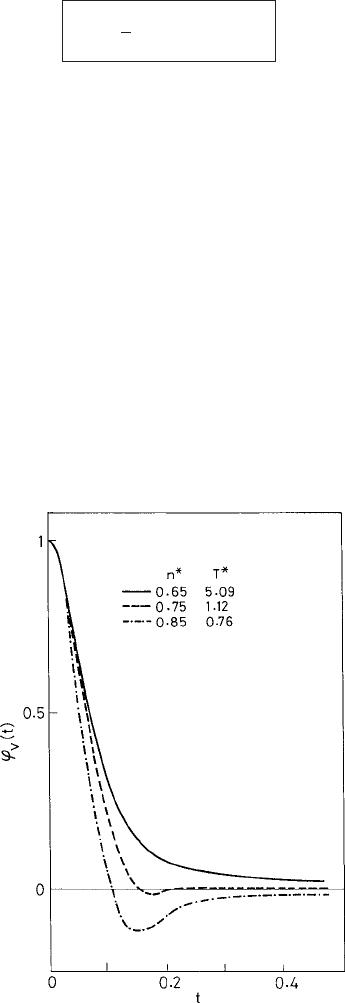
.InFig. 5.1 we show

Fig. 5.1 The tagged-particle velocity autocorrelation function ϕ

(t) vs. time t for a Lennard-Jones

ﬂuid at various values of the temperature T

∗

and density n

∗

. The dimensionless units are as given in

(5.2.28).FromLevesque and Verlet (1970).

 American Physical Society.