Das Sh.P. Statistical Physics of Liquids at Freezing and Beyond

Подождите немного. Документ загружается.

4.3 The landscape paradigm 191

Fig. 4.9 The time evolution of the overlap function q(t) deﬁned in (4.3.20) vs. time t for packing

fractions η ≡ ϕ = 0.312 (solid line), 0.440 (short-dashed line), and 0.491 (long-dashed line). Time

is expressed in Monte Carlo steps per site. Reproduced from Fuchizaki and Kawasaki (1998).



Physical Society of Japan.

in the single minimum within the time scale of the computation. For values of the packing

fraction beyond ϕ =0.49 with the initial time scale τ

∼1000 Monte Carlo steps (MCSs)

per site, the function q(t) relaxes at two different levels: ﬁrst, at t ∼20 000 MCSs and then

at t ∼60 000 MCSs per site. This is interpreted as the system being initially trapped in

a local free-energy minimum and eventually relaxing towards the states with lower free

energies through thermally activated hopping.

Earlier than these works Dasgupta and Valls (1994) studied the dynamics of free-energy

landscapes by locating the free-energy minimum of the RY functional mentioned above

nearest to an initial metastable conﬁguration of the density ﬁeld ρ. These initial conﬁgura-

tions {ρ(x)} were the ones reached by simulating the nonlinear Langevin equations (to be

discussed in the next chapter) on a grid. Their results are also consistent with a crossover

from a dynamics around the uniform liquid-state minimum at high temperature to an

activated-hopping scenario at low temperatures. The above study of the dynamics suggests

the following scenario for the dynamics for a hard-sphere system. At low densities the sys-

tem essentially ﬂuctuates around the liquid-state minimum. The relaxation time grows with

increasing density. At this initial stage of supercooling the liquid-state dynamics is still con-

trolled by continuous-ﬂuid-type motion of the particles. As the packing fraction increases

beyond a crossover value ϕ

the dynamics is controlled by thermally activated hopping of

the system in the free-energy landscape to conﬁgurations having inhomogeneous density

distributions. In the high-density state the system is caught in a local minimum of the free

energy with only vibrational motion in the free-energy basin. In real space this implies that

the particles vibrate around their mean positions lying on a disordered lattice structure. As

192 The supercooled liquid

the temperature of the liquid is supercooled to the glass-transition temperature T

the liquid

essentially freezes into a solid and attains a ﬁnite shear modulus.

4.4 Dynamical heterogeneities

A characteristic behavior seen in a deeply supercooled liquid suggests that the dynamics

in some regions of the system can be orders of magnitude faster than that in the neigh-

boring regions. Indeed, with time the nature of the heterogeneity seen in one region of

the space changes and is redistributed (Stillinger and Hodgdon, 1994; Cicerone and Edi-

ger, 1996). This spatially heterogeneous nature of the dynamics of the undercooled liquid

has been an area of much current research interest. The study of the dynamical hetero-

geneities generally refers to the length scales over which they occur and most naturally to

the corresponding time scales over which they exist.

Dynamical heterogeneities have important consequences for the transport properties of

supercooled liquids. The relaxation of a typical correlation function in a supercooled liquid

follows the stretched exponential form,

C(t) ∼ exp

−(t/τ )

, (4.4.1)

where τ is the relaxation time. The stretched-exponential exponent β decreases from its

high-temperature value of unity (simple exponential relaxation or what is termed Debye

relaxation) to smaller values near the glass-transition temperature T

. Generally stretched-

exponential relaxation is interpreted as a consequence of having several characteristic

relaxation times, i.e., expressed in terms of the distribution of the relaxation time τ by

g(τ ) as

C(t) ∼



∞

dτ g(τ )e

−(t/τ )

. (4.4.2)

The stretching of the relaxation in the supercooled liquid can be interpreted as a conse-

quence of the distribution of relaxation modes (each being exponential) corresponding to

the spatially heterogeneous dynamics from different regions of the system.

The observation of such heterogeneities in deeply supercooled liquids has been made

through dynamic hole-burning experiments (Schmidt-Rohr and Spiess, 1991; Cicerone and

Ediger, 1995; Schiener et al., 1997). Fujara et al. (1992) showed by means of NMR exper-

iments that a strong slowing down of translational diffusion occurs with supercooling.

In a very standard glass former, o-terphenyl (OTP), translational diffusion has a weaker

temperature dependence than the viscosity and rotational correlation time. The size of

regions over which the dynamics becomes heterogeneous grows strongly with temperature

on approaching T

. The length scale over which the dynamics of a single particle becomes

simple diffusive grows much longer as the temperature approaches T

. NMR experiments

have been used (Tracht et al., 1999) to measure directly the size of regions with hetero-

geneous dynamics. In our discussion in the present book we focus in particular on the

aspects of dynamic heterogeneities observed in computer MD simulations. These studies

4.4 Dynamical heterogeneities 193

are generally limited to much simpler molecules and much shorter time scales than those

in real experiments. However, a number of interesting characteristics of the dynamics can

be identiﬁed since the dynamics is probed here at a very microscopic level.

4.4.1 Computer-simulation results

The simplest quantity representing the structure of the disordered liquid is the pair correla-

tion function g(r) or the static structure factor S(k) discussed in the earlier chapters. It has

been widely found in simulations (Kob, 2003) that the liquid does not undergo any drastic

change in its equilibrium structure with an increase in supercooling. On the other hand, the

liquid dynamics becomes increasingly slow in the metastable supercooled state. The slow-

ing down with fall of temperature in the present context is far more drastic than the fall in

the average speed of the particles (∝

√

T ). The characteristic relaxation time corresponding

to the time correlation functions (introduced in Section 1.3) grows by orders of magnitude

when the liquid is supercooled. This is generally manifested in a two-step relaxation pro-

cess. At short times, i.e., times less than the average collision time between two particles,

the dynamics is of free-particle type (see eqn. (1.3.33) for example). This is followed by the

dissipative dynamics in which the correlation function decays to zero. At high temperature

this ﬁnal relaxation process is exponential and the corresponding relaxation time grows at

lower temperatures. However, with increasing supercooling or an increase of density, the

nature of the decay of the correlation function shows a qualitative change. The correlation

function after the initial ballistic regime remains on a plateau for some time (on a logarith-

mic time axis) and ﬁnally decays to zero. This two-step process is a very typical feature

of the dynamics of the dense liquid state. This behavior is most easily demonstrated by

considering the tagged-particle correlation F

(q, t) (see eqn. (1.3.23) for its deﬁnition) in

a dense ﬂuid. In Fig. 4.10(a) the decay of the tagged-particle correlation in a binary mix-

ture is displayed for a wave vector near the structure-factor peak. For high temperature the

correlation decays exponentially, and it develops a plateau as the temperature is lowered.

The dynamics of the supercooled liquid becomes increasingly heterogeneous in different

regions. To illustrate this further, let us consider the plot of the mean-square displacement

r

(t) with respect to time. This is shown in Fig. 4.10(b). For short times the mean-square

displacement grows as t

, conforming to the free-particle behavior. At low temperatures

the mean-square displacement remains on a plateau over an intermediate time scale. This

behavior signiﬁes rattling of the tagged particle in the cage formed by surrounding par-

ticles. With increasing density the cages persist for longer time and hence the length of

the plateau increases. However, the height of the plateau remains the same, indicating that

the size of the cage does not drastically change with the fall of temperature. Over longer

times the mean-square displacement grows linearly in time, indicating the self-diffusion

process. Over this ﬁnal time range the slope of the r

(t) vs. t curve gives the diffusion

coefﬁcient D

through the Einstein relation (1.4.27). D

falls by a few orders of magnitude

in these systems. If the glass transition is considered as a jamming transition in which the

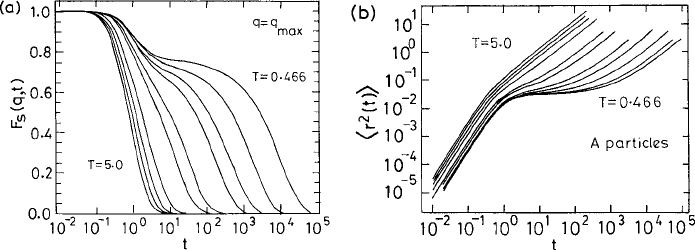
194 The supercooled liquid

Fig. 4.10 Single-particle dynamics for the A particles in a BMLJ system. (a) The tagged-particle

density correlation F

(q, t) at q = q

, the ﬁrst peak of the static structure factor. (b) The mean-

square displacement r

(t) vs. time t. The curves from right to left in both (a) and (b) correspond

to temperatures T = 5.0, 4.0, 3.0, 2.0, 1.0, 0.8, 0.6, 0.55, 0.50, 0.475, and 0.466. Reproduced from

Kob and Andersen (1994). Both parts

 American Physical Society.

particles are trapped for long times then this will imply that with supercooling the break-

ing of the cage, or, for a tagged particle, escaping from its cage, becomes a very slow

process.

In the supercooled state the relaxation process becomes spatially heterogeneous. The

detailed nature of this heterogeneity has been investigated in a number of studies using

MD simulations (Perera and Harrowell, 1998; Yamamoto and Onuki, 1998a). A key aspect

of this dynamical heterogeneity is violation of the Stokes–Einstein (SE) relation D

η/T =

constant which relates the translational diffusion D

to the shear viscosity (see eqn. (1.4.28)

in Chapter 1). The SE relation generally holds in normal liquids but breaks down with

increased supercooling (Fujara et al., 1992; Chang et al., 1994; Cicerone and Ediger, 1995,

Cicerone et al., 1995; Blackburn et al., 1996).

The translational diffusion constant D

is found to be larger than that expected from the

SE relation, although the rotational diffusion continues to scale with the shear viscosity η.

The temperature dependences of 1/D

and η are different in the supercooled region. A

phenomenological explanation of this behavior has been provided in terms of the existence

of a spatially heterogeneous and transient distribution of local relaxation times (Perera and

Harrowell, 1998). The mean-square displacement and hence D

are controlled by the pres-

ence of a set of particles that are more mobile than the rest. The shear viscosity η,on

the other hand, is dominated by the relaxation of the slower regions. Molecular-dynamics

simulations of soft disks in two dimensions by Perera and Harrowell (1998) provided evi-

dence for such a heterogeneous distribution. Simulations of a similar soft-sphere mixture

with slightly different parameters (Yamamoto and Onuki, 1998a) demonstrated the hetero-

geneous nature of the diffusion of a tagged particle of a three-dimensional ﬂuid. The van

Hove self-correlation function G

(r, t) (see eqn. (1.3.29) for its deﬁnition) in the deeply

supercooled state has a large-r tail that scales as r/t

1/2

for t ≤ 3τ

(Yamamoto and Onuki,

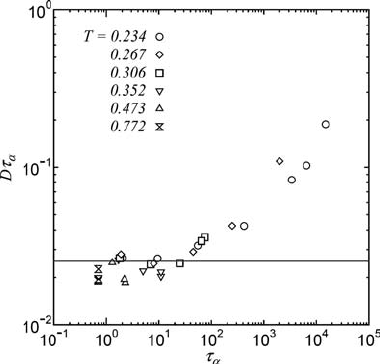
4.4 Dynamical heterogeneities 195

Fig. 4.11 The breakdown of the Stokes–Einstein relation seen in simulations of a soft-sphere binary

mixture, in a plot of the self-diffusion coefﬁcient D

times the α-relaxation time τ

vs. τ

. The solid

line represents the corresponding Stokes–Einstein value of D

. Reproduced from Yamamoto and

Onuki (1998a).

 American Physical Society.

1998a). This represents a departure from a simple diffusion process over time scales less

than that for relaxation of the heterogeneous structures (τ

). For times long compared with

the diffusion is homogeneous and the corresponding diffusion coefﬁcient is determined

from the mean-square displacement. In the high-temperature regime the stress-relaxation

time τ

and the self-diffusion coefﬁcient D

scale according to the SE law. Deviation

from this is observed, with an enhanced diffusion coefﬁcient, as the liquid is increasingly

supercooled. This is displayed in Fig. 4.11.

The van Hove self-correlation function G

(r, t) obtained from the computer simulation

of a BMLJ type-I system in the supercooled region has been very useful for a careful analy-

sis of the heterogeneous dynamics. In the discussion of G

(r, t) in Chapter 1 (Section 1.3.2)

we have seen that for the isotropic ﬂuid a strictly Gaussian form of this function is entirely

determined in terms of the mean-square displacement of the tagged particle r

(t).The

departure from Gaussian behavior is expressed in terms of the non-Gaussian parameter

(t) deﬁned in eqn. (1.3.61). The latter involves the quantity r

(t) and in fact relates

to four-point correlation functions in the liquid. Indeed, it follows from eqns. (1.3.53) and

(1.3.54), respectively, that the self-diffusion coefﬁcient D

is determined in terms of a two-

point velocity correlation function, while the non-Gaussian parameter α

(t) is linked to a

four-point velocity correlation function. The non-Gaussian parameter α

(t), obtained from

the computer simulation (Kob et al., 1997) of the BMLJ type-I system, has a peak at times

intermediate between the short-time ballistic regime and the structural-relaxation time τ

This is shown in Fig 4.12(a). The height of the peak as well as the time t

at which the peak

appears increases with the fall of temperature.

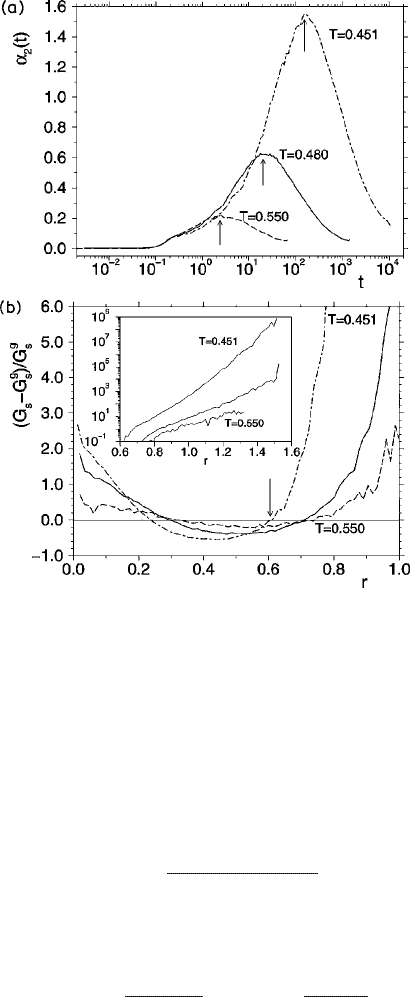
196 The supercooled liquid

Fig. 4.12 The non-Gaussian parameter α

(t) vs. time t for T = 0.550, 0.480, and 0.451. The arrows

indicate the peak t

of the corresponding α

(t).(b)(r, t) deﬁned in eqn. (4.4.3) vs. r at the time

t = t

obtained in (a). The temperatures are the same as for the corresponding curves in (a). The

arrow marks the location of r

for T = 0.451. The inset shows the same quantity on a log scale.

Reproduced from Kob et al. (1997). Both parts

 American Physical Society.

The tagged-particle correlation G

(r, t) has been used by Kob et al. to establish a crite-

rion for identifying a set of particles that are more mobile than the rest of the particles. The

relative difference is deﬁned as

(r, t) =

(r, t) − G

(r, t)

(4.4.3)

of the van Hove function from the corresponding Gaussian quantity G

(r, t). The latter is

obtained as

(r, t) =



2πr

(t)



3/2

exp



−

2r

(t)



(4.4.4)

in terms of the mean-square displacement r

(t) of the tagged particle of species A. From

aplotof(r, t

) vs. r (see Fig. 4.12(b)), one can identify a distance r =r

corresponding

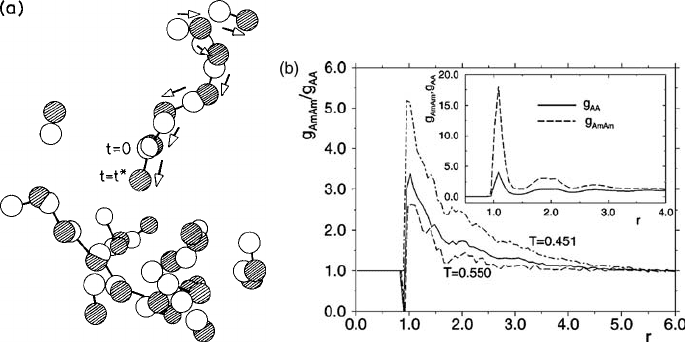
4.4 Dynamical heterogeneities 197

Fig. 4.13 (a) A demonstration of the string-like cooperative dynamics seen in simulation of a super-

cooled BMLJ system. Mobile particles (see the text for their deﬁnition) in the subregion of the

simulation box are shown at two different times, t = 0 (light spheres) and the same particle at a

later time (shaded spheres), with the bold dark lines connecting the corresponding pairs for identi-

ﬁcation. Arrows mark the paths followed by some of the particles. Reproduced from Donati et al.

(1998). (b) From the BMLJ simulations of Fig. 4.12. The inset shows the radial distribution functions

of particles of type A, g

for the bulk particles and g

AmAm

for the corresponding mobile particles

at temperature T =0.451 in reduced units. The main ﬁgure of part (b) shows the ratio between the

two types of correlation g

and g

AmAm

for T =0.550, T =0.480, and T =0.451. Reproduced

from Kob et al. (1997). Both parts

 American Physical Society.

to the maximum r at which (r, t

) vanishes. Particles that have traveled a distance r > r

within a time t

are then deﬁned as “mobile” particles. Snapshots of these mobile parti-

cles show that they tend to form a cluster. The regions involved in these clusters are not

compact but string-like. A superposition of two successive snapshots of a set of mobile

particles is shown in Fig. 4.13(a). Explicit tracking of the mobile particles shows that they

undergo a string-like motion. The average string length increases with decreasing temper-

ature. The correlated nature of the dynamics of the mobile particles is manifested in the

corresponding pair correlation function g

AmAm

of the mobile particles. The ratio R

the pair correlation function g

AmAm

to that of the bulk particles g

of species A is large

> 1) at small r and decays to 1 for large r. R

grows with lowering of the tempera-

ture, displaying enhanced correlation in the deeply supercooled state. The behavior of the

ratio of pair correlation functions is shown in Fig. 4.13(b). The time correlation G

(r, t)

for the mobile particles decays faster than the corresponding bulk G

(r). Finally, the prob-

ability P(t) that a particle that is mobile at t =0 continues to remain so at t =t falls with

time t. The time scale of the decay for P(t) is the same as that of the corresponding G

for the mobile particles. Synchronous movements of a set of ﬂuid particles have been used

to search for a suitable mechanism for a ﬂuid particle to escape from the surrounding cage

(Langer, 2006a, 2006b) in the supercooled liquid. The formation of the string-like motion

198 The supercooled liquid

as described above is a signature of the dynamical heterogeneities in the dense system over

intermediate time scales. However, its relevance in producing the extremely slow dynamics

near glass formation is unclear at this stage.

4.4.2 Dynamic length scales

In the discussion of dynamical heterogeneities in the supercooled liquid in the previous

section we have seen that in the supercooled liquid a set of particles is more mobile than

the rest and they tend to form a cluster or string-like structure. The time scale of this string-

like cooperative dynamics deﬁnes the time over which dynamical heterogeneities persist.

These observations naturally give rise to speculation about whether a growing correlation

length can be associated with the supercooled liquid state. Various efforts (Dasgupta et al.,

1991; Ernst et al., 1991) to identify such a length scale associated with the supercooled

state have been made. In the following we will discuss some of the more recent results

seen in simulations of liquids in the metastable supercooled state.

In order to focus on the cooperative nature of the dynamics it is useful to consider the

possible correlation in the respective displacements over time t between two particles situ-

ated at two spatial points separated by a distance r at an initial time “0.” The displacement

(0, t) of the ith particle from time 0 to t is deﬁned as

(t, 0) = r

(t) − r

(0). (4.4.5)

We have dropped the vector notation on μ

and r

to avoid clutter. The average of μ

(t, 0)

is the same for all particles in the liquid at equilibrium. Hence the displacement ﬂuctuation

is obtained as

μ

(0, t) = μ

(t, 0) −μ(t, 0). (4.4.6)

The correlation of this displacement over time t for two different particles i and j is deﬁned

in terms of the correlation function S

(r, t) as

(r, t) =

i, j

μ

(0, t)μ

(0, t)δ(r −r

(t))

i, j

δ(r − r

(t))

, (4.4.7)

where r

(t) = r

(t) − r

(t). The denominator on the RHS is in fact the pair correlation

function g(r) in the liquid. The function S

(r, t) in fact involves the information from

four different points, (0, 0), (0, t), (r, 0), and (r, t). If the ﬂuctuations of μ

and μ

are completely uncorrelated (for two points that are widely separated), we have S

(r, t) =

μ

→0. At a given time t the correlation function S

(r, t) integrated over all distances

r is a time-dependent function involving the correlation of four points and hence can be

denoted as

4.4 Dynamical heterogeneities 199

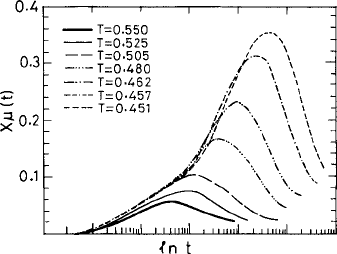
Fig. 4.14 The mobility correlation function χ

(t) vs. time t at various temperatures from a

simulation of a BMLJ system. Reproduced from Donati et al. (1999).

 American Physical

Society.

(t) =



dr S

(r, t). (4.4.8)

At a certain time t,ifS

(r, t) is not falling off fast enough (long-ranged) with r then χ

(t)

will develop a peak at that ﬁxed time. From MD simulation of a BMLJ type-I system

Donati et al. (1999) obtained the function χ

(t) at several temperatures in the supercooled

region. We show in Fig. 4.14 that the correlation χ

(t) exhibits a distinct peak at t =

∗

.Botht

∗

and the peak height increase as the liquid is increasingly supercooled. The

height of the peak also increases with fall of temperature. Indeed, as noted above, the

peak in χ

(t) at t = t

∗

indicates a slower spatial decay of the function S

(r, t

∗

).For

simulations of polymer melts similar results were obtained (Bennemann et al., 1999). The

at different temperatures scaled with respect to their corresponding values at the peak t

∗

collapse into a single curve. If the spatial decay of this function is associated with a length

scale, then the increase in the peak of χ

at lower temperature implies a corresponding

growth in the correlation length ξ

(T ). Note that this enhanced correlation occurs only near

∗

and therefore the associated correlation length ξ

(T ) is purely dynamical. Multi-particle

correlation functions have been investigated widely in order to reach a growing correlation

length (Berthier et al., 2005, 2007a, 2007b). The above treatment in terms of the four-

point functions can be generalized to identify an order parameter for the supercooled liquid

state.

Density ﬂuctuations play a very crucial role in describing the liquid state, and the time

correlation function of density ﬂuctuations is therefore a key quantity of interest. We will

see in subsequent chapters that a discontinuous change in the long-time limit of the den-

sity correlation function is used to deﬁne a dynamic transition in the supercooled liquid.

Let us denote ψ(x, t) ≡ δρ(x, t)δρ(x, 0). For the ergodic liquid we have for the density

correlation function

lim

t→∞

δρ (x, t)δρ(x, 0)= lim

t→∞

ψ(x, t)=0. (4.4.9)

200 The supercooled liquid

On the other hand, the RHS of the deﬁnition (4.4.9) getting frozen at a nonzero value

deﬁnes the nonergodic state. The discontinuous change in the time correlation function

δρ (x, t)δρ(x, 0) represents the nonergodicity parameter.

Let us now generalize this beyond the two-point level. Speciﬁcally, we consider the

four-point correlation function, which has been of much current interest for understanding

the physics of supercooled liquids. Starting from this, we deﬁne the four-point function

(x, t) in terms of the spatial correlation of ψ(x, t),

(x, t) =δρ (0, t)δρ(0, 0)δρ(x, t)δρ(x, 0)

−δρ (0, t)δρ(0, 0)δρ (x, t)δρ(x, 0)

=ψ(0, t )ψ(r, t)−ψ(0, t)ψ(r, t). (4.4.10)

If we deﬁne the bulk property φ(t) corresponding to ψ(x, t),

φ(t) =



dx ψ(x, t ), (4.4.11)

then it follows that one can deﬁne a four-point susceptibility function χ

(t) as

(t) =



dx G

(x, t)



ψ(x, t)ψ(y, t)−ψ(x, t)ψ(y, t)

= V

+

(t)

−φ(t)

. (4.4.12)

Using the above approach, the four-point correlation function of a BMLJ mixture of type

I was been investigated by Berthier et al. (2007a, 2007b). In this case the correlations

are deﬁned using the tagged-particle density ρ

(x, t). In terms of the Fourier-transformed

quantities we deﬁne the two-point function ϕ

(k, t) as

(k, t) =



i=1

(k, t)ρ

(−k, 0), (4.4.13)

where ρ

(k, t) = exp(ik · r

(t)) and N

is the total number of particles of the species

A. The intermediate scattering function is obtained as F

(k, t) =ϕ

(k, t).Usingthe

deﬁnition for the four-point function given in eqn. (4.4.12), the corresponding result for

the tagged particle in the present case is obtained as

(t) = N



+

(k, t)

− F

(k, t)

. (4.4.14)

The sum over the wave vector on the RHS of the expression for χ

(t) has been approx-

imated by keeping only the dominant contribution at k = k

corresponding to the peak

In general the characteristic order parameter of the ergodic–nonergodic (ENE) transition is expected to be deﬁned in terms of

the difference between some property of the system being calculated using a complete ensemble average and the same

property evaluated by taking an inﬁnite-time average. We pursue here a different approach using a restricted phase-space

average and deﬁne the transition in terms of a ﬁnite jump in the long-time limit of the crucial density–density correlation

function. The average

ψ(x , t) is therefore the order parameter for the ENE transition.