Das Sh.P. Statistical Physics of Liquids at Freezing and Beyond

Подождите немного. Документ загружается.

4.4 Dynamical heterogeneities 201

of the structure factor and is also angularly averaged for the isotropic system. A plot of

the simulation data of χ

(t) for the species A of the BMLJ type-I system displays a clear

peak (Berthier et al., 2007a, 2007b) at t =t

∗

(say). This represents a time scale over which

the correlation is strongest and is found to be less than the structural-relaxation time in the

supercooled liquid.

A correlation length ξ(T ) is also identiﬁed from the above analysis of the four-point

correlation functions. For this we deﬁne the spatial ﬂuctuation of the instantaneous value

of the self-intermediate scattering function

δϕ

(q, k, t) =



iq · r

(0)



cos(

k(r

(t) − r

(0)))F

(k, t)

. (4.4.15)

Let us consider δϕ

(q, k, t) for a ﬁxed k = k

near the structure-factor peak, angular aver-

aged and denote this as δϕ

(q, t). The four-point dynamic structure factor is obtained as

(q, t) =



δϕ

(q, t)δϕ

(−q, t)



. (4.4.16)

The above correlation has been angularly averaged over different directions of q to

obtain the corresponding result for the isotropic liquid as a function of only the magni-

tude of q. The averaged function denoted simply as S

(q, t) is directly obtained from the

simulation data. S

(q, t = t

∗

) at the time t = t

∗

at which χ

develops a peak near q → 0

and is ﬁtted to the following Ornstein–Zernike form:

(q, t

∗

) =

(q = 0, t

∗

)

1 + (qξ)

. (4.4.17)

In the above ﬁtting α is a ﬁtting parameter. The four-point function is determined for

different values of q lying within the range allowed by the size of the simulation box.

The simulation data at different temperatures are compatible with the value α ≈ 2.4in

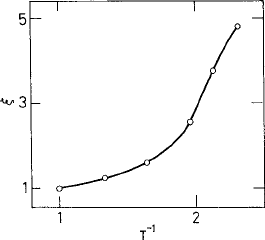
the above ﬁtting form and give a dynamic correlation length ξ(T ). This is displayed in

Fig. 4.15. Although the growth of the correlation length ξ with the fall of temperature

is not as drastic as it is near the critical point, it increases with increasing supercooling.

Besides the four-point functions, three-point correlation functions or response-type func-

tions have also been linked to a corresponding correlation length that is similar to the above

form. Berthier et al. (2007a, 2007b) considered the three-point correlation

(q, t) =



δϕ

(q, t)δe(−q, t)



(4.4.18)

linking the tagged-particle density to the ﬂuctuation of the energy density at time t accord-

ing to

e(q, t) =



iq · r

(t)

(t) −e], (4.4.19)

where e

(t) = p

/(2m) +

u(r

(t)) is the energy of the ith particle at time t and e

is the average energy per particle. The ﬁtting of the angularly averaged S

(q, t) to the

Ornstein–Zernike form (4.4.17) corresponds to the parameter value α = 3.5 and the same

202 The supercooled liquid

Fig. 4.15 The length scale ξ obtained from analysis of the four-point correlation function S

(q, t) as

well as the three-point functions S

(q, t) (see the text) vs. the inverse temperature 1/T . The results

correspond to MD as well as Monte Carlo simulations of a BMLJ system. The y axis is a linear scale.

Reprinted from Berthier et al. (2007a).

 American Institute of Physics.

correlation length ξ(T ) as that displayed in Fig. 4.15. Fitting of the four-point functions

calculated from MD simulations to ﬁnite-size scaling has also been used to extract a grow-

ing correlation length in the supercooled state (Karmakar et al., 2009). In all these cases the

correlation length calculated from the computer simulations of a small number of particles

in a box grows with supercooling and approaches the system size.

Independently from the above analysis, a dynamic length scale has also been identiﬁed

from considerations pertaining to the propagating shear waves in the supercooled liquid.

In general, shear waves of very short wavelengths can exist even in a normal liquid, giving

a characteristic solid-like response to a very-high-frequency perturbation. Thus, at a given

temperature the liquid can sustain shear waves of a maximum wavelength. This maximum

wavelength l

(say) or corresponding minimum wave number q

min

= 2π/l

grows with the

fall of temperature. This was observed in the MD simulation (Mountain, 1995)ofa50: 50

soft-sphere mixture of size ratio 1.2. The length l

grows with increasing supercooling.

In general, for a soft-sphere potential of u(r) = (σ/r)

, the thermodynamic prop-

erties at density n

and temperature T (T = (k

β)

−1

) are expressed in terms of a single

dimensionless parameter 

eff

=(β)

3/n

, which increases with supercooling. A binary

mixture of soft spheres with an equimolar mixture of particles of masses m

and 2m

and

diameters σ

and σ

(σ

= (σ

+ σ

)/2), respectively, interacting with u

(r) =

(σ

/r)

, with the parameter 

eff

= (β)

1/4

, is considered. The simulation of this

mixture showed that, with a change of 

eff

from 0.9 to 1.4, the length scale l

is seen to

grow by an order of magnitude. The increase of l

is essentially linked to that of the shear

viscosity, which sharply increases with supercooling.

A common feature among the different types of dynamic length scales identiﬁed from

computer simulations of the supercooled liquids is the following: all of them grow during

the initial stages of supercooling and ﬁt well to a power-law divergence around some lower

temperature T

. However, before T

is reached the power-law divergence is cut off and the

correlation length ξ

is ﬁnite at T

.WewillseeinChapter 8 that at the theoretical level this

4.4 Dynamical heterogeneities 203

behavior of the dynamic correlation length is linked to a crossover in the dynamics of the

liquid around a characteristic temperature T

that lies between the freezing point T

and the

laboratory glass-transition point at T

. This has been achieved by extending the statistical-

mechanical model for the liquid-state dynamics to the supercooled region. In particular,

this involves understanding the strongly correlated motion of the ﬂuid particles as well as

the effects of liquid structure on the dynamics at high density. We have discussed above the

evidence for such correlations in the dynamics as seen in computer simulations. To develop

the theoretical models for the dynamics, we will ﬁrst introduce the proper formalism and

derive an appropriate model for the time dependence of the correlation. This is discussed

in the next three chapters.

Dynamics of collective modes

Theoretical developments on the dynamics of a dense liquid using a statistical-mechanical

approach primarily involve a small set of slow collective densities termed hydrodynamic

modes. The time scales of relaxation of these modes are much longer than those for the

microscopic modes of the system. The basic approach adopted here is the analysis of

the time correlation functions (introduced earlier in Chapter 1) of the slow modes. In

the present chapter and the next two chapters we discuss microscopic methods for cal-

culating the correlation functions involving the ﬂuctuation or hydrodynamic approach. We

focus primarily on the simplest type of correlation functions involving ﬂuctuations at two

different spatial and time coordinates. Owing to time translation invariance, equilibrium

two-point correlation functions of hydrodynamic modes at the same time over different

spatial points are time-independent and provide us with information on the thermodynamic

behavior of the system. On the other hand, the dynamic behavior of the system is linked

to the correlation of physically observable quantities at two different times. The time cor-

relation function of density ﬂuctuations is particularly important for our discussion of the

slow dynamics in a liquid. In the simplest of the theoretical models, the decay of the corre-

lation with time is exponential. We discuss here how such exponential relaxation behavior

can be understood using linear dynamics of the ﬂuctuations. The formalism developed in

the later parts of this chapter allows in a natural way the extension of the macroscopic

hydrodynamics to intermediate length and time scales, and is referred to as generalized

hydrodynamics. At low densities or high temperature we obtain the standard forms of the

correlation function for the normal liquid state. For liquids supercooled below the freezing

point T

, this approach ﬁnally leads to a set of microscopic models for the slow dynamics

observed in those systems. This development is discussed in the next two chapters. The

primary result predicted from these models is a crossover in the dynamic behavior of the

liquid at a temperature below T

, i.e., in the moderately supercooled state. The character-

istic temperature around which this happens has been termed the mode-coupling-theory

(MCT) transition temperature T

. The present chapter is aimed at introducing some basic

concepts for the liquid-state dynamics. We ﬁrst obtain the basic conservation laws for the

liquid and demonstrate how they give rise to the dissipative equations of hydrodynam-

ics. The hydrodynamic correlation functions and the expressions for transport coefﬁcients

204

5.1 Conservation laws and dissipation 205

follow next. We then introduce the linear equations of the ﬂuctuating hydrodynamics,

which form the basis of the discussion in the subsequent chapters.

5.1 Conservation laws and dissipation

In a ﬂuid with a large number of particles moving and colliding at random the average

time between successive collisions of the ﬂuid particles is extremely short, ∼10

−15

s, even

at moderate liquid densities, and it decreases with increasing density. The corresponding

mean free path also shortens as the liquid becomes more dense. Within the background

of this apparently chaotic dynamics there are some collective modes in the many-particle

system relaxing over time scales that are many orders of magnitudes longer than those

for the fast modes. The dynamic behavior of a ﬂuid is described primarily in terms of the

relaxation of a few such slow modes. As we will see in subsequent chapters, there are

several reasons for the occurrence of the slow modes, such as microscopic conservation

laws or breaking of some continuous symmetry of the microscopic Hamiltonian, or even

some associated slow parameter such as the heavy mass of a Brownian particle. The most

basic dynamic variables giving rise to the equations of macroscopic hydrodynamics for

the ﬂuid relate to conserved properties of the ﬂuid. In an isotropic system there are ﬁve

conserved densities corresponding to the total mass, momentum, and energy.

5.1.1 The microscopic balance equations

In terms of the actual phase-space coordinates of the constituent particles, the microscopic

density at a given point r at time t is deﬁned as

ˆρ(r, t) =



mδ(r − r

(t)), (5.1.1)

g(r, t) =



δ(r − r

(t)), (5.1.2)

ˆe(r, t) =



δ(r − r

(t)), (5.1.3)

where we have used the deﬁnition e

= p

/(2m) +(1/2)



u(r

αβ

), with the prime in the

sum implying that the α = β term is absent from the sum. We put a hat on the slow variable

to indicate the dependence on the phase-space coordinates of this variable. Note that the

mass density ˆρ(r, t) is similar to the single-particle density n(r, t) deﬁned in eqn. (1.2.76).

For the one-component system in fact we have ˆρ = m ˆn. The signiﬁcance of the above

deﬁnitions for the microscopic variables is apparent in the coarse-grained picture. Thus,

for example, with the above deﬁnition for the density ˆρ(r), its integral over all volume is

equal to the total mass of the system mN, which is a conserved quantity. The respective

conserved densities ˆa(r) ≡{ˆρ(r),

g(r), ˆe(r)} satisfy the following microscopic-balance

equations (for their deduction starting from the microscopic deﬁnitions (5.1.1)–(5.1.3) see

Appendix A5.1):

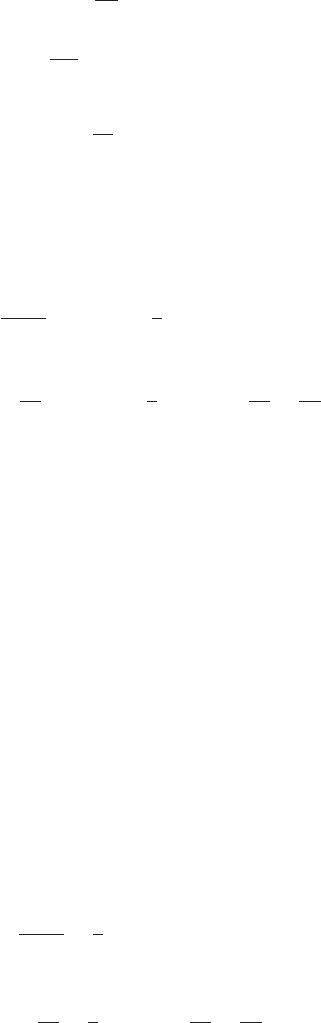
206 Dynamics of collective modes

∂ ˆρ

∂t

+∇·

g = 0, (5.1.4)

∂ ˆg

∂t



∇

ˆσ

= 0, (5.1.5)

∂ ˆe

∂t

+∇·

= 0, (5.1.6)

with the corresponding currents being given by

g(r) =



δ(r − r

), (5.1.7)

ˆσ

(r) =



δ(r − r

) +





α,β



αβ



αβ

, (5.1.8)

(r) =



δ(r − r

) +





α,β



αβ







αβ

, (5.1.9)

where we have used the deﬁnitions of the following quantities in terms of the force F

αβ

acting on the particle at r

due to the particle at r



αβ



ds δ(r − r

+ sr

αβ

), (5.1.10)



αβ

= (r

αβ

· F

αβ

)ˆr

αβ

ˆr

αβ

. (5.1.11)

ˆr

αβ

is the ith component of the unit vector

αβ

. Note that 

αβ

= 

βα

, and the quantity



αβ

is also symmetric under exchange of {α, β} as well as {i, j}. The microscopic stress

tensor is symmetric,

¯σ

. The microscopic-balance equations obtained above with

the formal manipulations are exact and symmetric under time reversal. However, they are

not local in nature. In the case of short-range potentials the force F

αβ

between the two

particles is appreciable only if R

αβ

is small. In this limit we can ignore the last part in the

argument of the delta function in eqn. (5.1.10) such that 

αβ

= δ(r − r

) and obtain the

currents in the local form as follows:

ˆσ

(r) =



⎡

⎣





α,β



αβ

⎤

⎦

δ(r − r

), (5.1.12)

(r) =



⎡

⎣





α,β



αβ





⎤

⎦

δ(r − r

). (5.1.13)

5.1 Conservation laws and dissipation 207

5.1.2 Euler equations of hydrodynamics

The above microscopic equations for the slow conserved densities are reversible in time.

These are exact balance equations. In order to obtain the hydrodynamic equations for the

smoothly varying local densities of mass, momentum, and energy respectively denoted

by {ρ(r, t), g(r, t), e(r, t)}, we need to average the above balance equations. The aver-

aging in principle needs to be done over the nonequilibrium ensemble. Indeed, if the

system is in equilibrium then by averaging the densities one obtains the corresponding

time-independent equilibrium value. The nonequilibrium average is obtained by extending

the notion of the Gibbsian ensemble to include systems that are out of equilibrium. In this

regard the nonequilibrium system which we describe here is assumed to be in the time

regime where it has reached a state of local equilibrium. This is termed the stage at which

the set of local densities {ˆa(r)} is sufﬁcient to describe the state of the system. This is a

plausible hypothesis, particularly at high densities, since the stage of local equilibrium is

reached rapidly through frequent inter-particle collisions. The probability function for the

local equilibrium state is obtained in analogy with that of the equilibrium state. For the

equilibrium state with a set of extensive conserved quantities A ={N, H, P,...},wehave

the canonical distribution (1.2.7), i.e.,

) ∼ exp[−β(H − μN +P · v)]. (5.1.14)

The respective intensive thermodynamic variables given by the set b ={β, μ,v} refer

to the temperature, chemical potential, and velocity, respectively. Analogously, the local

equilibrium state is characterized by the nonuniform densities

a(r) ≡{ˆe,

g, ˆn} with the

distribution function

(

, t) = Q

−1

exp

−



dr β(r, t)



ˆe(r) − v(r, t) · ˆg(r)

−



μ(r, t) −

(r, t)



ˆn(r)

4

, (5.1.15)

where we denote the phase point 

by the set of 6N variables 

≡{r

, p

,...,r

, p

The number density ˆn is deﬁned as m ˆn(r) =ˆρ(r). Q

−1

is the necessary normalization

constant, which therefore satisﬁes the relation

= Tr

⎡

⎣

exp

⎧

⎨

⎩

−





{a}

(r, t) ˆa(r)

⎫

⎬

⎭

⎤

⎦

. (5.1.16)

The conserved property A (extensive) deﬁnes the local density ˆa(r),

A =



dr ˆa(r). (5.1.17)

is the corresponding local thermodynamic property (intensive) in terms of which the

local equilibrium is deﬁned. The local ensemble average of ˆa is obtained from the relation

208 Dynamics of collective modes

ˆa(r)

=−

δ ln Q

(t)

δα

(r, t)

. (5.1.18)

In the form considered in eqn. (5.1.15) we therefore have the following α

corresponding

to the set ˆa ≡{ˆe,

g, ˆn}:

= β(r, t)



μ(r, t) −

(r, t)



= β(r, t)v(r, t), α

= β(r, t). (5.1.19)

In analogy with the equilibrium case, the set of local thermodynamic variables is given by

{β(r, t), μ(r, t ), v(r, t)}, referring to the local temperature, local chemical potential, and

local velocity, respectively. These nonuniform parameters characterizing the local equilib-

rium are determined by imposing the self-consistency condition that the nonequilibrium

state average of a local density ˆa can be approximated by taking the average over the local

equilibrium distribution,

a(r, t) =ˆa(r)

=ˆa(r)

. (5.1.20)

The averaged local densities a(r, t) then are treated as smooth functions of the space and

time dependence, termed hydrodynamic ﬁelds. The time evolution of these nonuniform

densities in a state perturbed from the thermodynamic equilibrium is given by the average

of the balance equation for the corresponding microscopic densities {ˆa}, i.e.,

∂a(r, t)

∂t

+∇· j

= 0. (5.1.21)

The local equilibrium average j

of the microscopic currents

(r, t) for the one-component

ﬂuid presented in eqn. (5.1.7) is obtained in Appendix A5.1.1. We have

g ≡

g

= ρv, (5.1.22)

≡ˆσ



= Pδ

+ ρv

, (5.1.23)

≡





 +ρ

+ P



v, (5.1.24)

where v(xt) is the local velocity so that the ﬂuid appears to be at rest in the vicinity of this

point x from a frame moving locally with velocity v(xt). On substituting these equations we

obtain the Euler equations for the hydrodynamics for an ideal ﬂuid without any dissipative

effects,

∂ρ

∂t

+∇· g = 0, (5.1.25)

∂g

∂t



∇





+∇

P = 0, (5.1.26)

∂e

∂t

+∇·



(e + P)



= 0. (5.1.27)

5.1 Conservation laws and dissipation 209

The above set of equations for the slow modes {ρ,g, e} is invariant under time reversal

and represents reversible dynamics. In order to construct the equations for the irreversible

dynamics we need to include the dissipative effects. The forms of the dissipative terms in

the equations of motion are obtained in a phenomenological manner. To do this we consider

the rate at which the entropy of the ﬂuid is changing. The entropy of the ﬂuid in the local

equilibrium state is obtained by extending to this case the Boltzmann prescription relating

the thermodynamic entropy to the mechanical probability of the state,

S(t) =−



ln f

(

, t)



. (5.1.28)

We deﬁne the entropy density s(r, t) whose spatial integral gives the total entropy S(t),

S(t) =



dr s(r, t). (5.1.29)

The dynamics corresponding to the local-equilibrium description is described by the Euler

equations. It has been shown (see Appendix A5.1.2) that the entropy density s(r, t) satisﬁes

a continuity equation with a current sv:

∂s

∂t

+∇· (sv) = 0. (5.1.30)

There is no net production of entropy in the isolated system with reversible dynamics.

The positive entropy production is a signature of the irreversible or dissipative effects in

the ﬂuid.

5.1.3 Dissipative equations of hydrodynamics

The dissipative effects due to irreversible transport in the ﬂuid are included in the dynamic

equations for the local densities in a phenomenological manner. To make inferences about

the form of the dissipative terms, we extend the currents in the equations for the dynamics

in terms of a dissipative part,

≡ σ

+ σ

= Pδ

+ ρv

+ σ

, (5.1.31)

≡ j

+ j



 +ρ

+ P



v + j

. (5.1.32)

The corresponding equations of motion for the coarse-grained or averaged densities

ˆa(r, t ) are given by

210 Dynamics of collective modes

∂ρ

∂t

+∇· g = 0, (5.1.33)

∂g

∂t



∇

= 0, (5.1.34)

∂e

∂t

+∇· j

= 0. (5.1.35)

There is no dissipative part in the mass current g, which is itself a conserved quantity.

The continuity equation remains unaltered at the coarse-grained level. The other dissipa-

tive currents are expressed in terms of the gradients of the corresponding thermodynamic

properties such as the local temperature T (r, t ) = β

−1

(r, t) and velocity v(r, t),

=−η

ijkl

∇

, (5.1.36)



=−λ

∇

T, (5.1.37)

where the summation convention of repeated indices has been used. The tensor η

ijkl

and

refer to the viscosity and thermal conductivity of the liquid, respectively. In Appendix

A5.1.2 we demonstrate that the above forms for the dissipative currents (5.1.36) can be

argued from general thermodynamic considerations such as that of positive entropy pro-

duction in the irreversible process. For an isotropic ﬂuid the transport matrices are further

simpliﬁed,

ijkl

= η

(δ

+ δ

) +



−

2η



, (5.1.38)

= λδ

, (5.1.39)

where η

and ζ

correspond to the shear and bulk viscosities, respectively, while λ is

the thermal conductivity. The constant coefﬁcients on the RHS of (5.1.38) are chosen

such that the transverse modes couple to the shear viscosity η. The second term in the

expression for σ

in (5.1.31) keeps the equations of hydrodynamics invariant under a Gal-

lelian transformation. A set of hydrodynamic equations for the averaged local densities

{ρ(r, t), g(r, t), (r, t)} is then obtained in the following form:

∂ρ

∂t

+∇· g = 0, (5.1.40)

∂g

∂t

+∇





+∇

P − L

= 0, (5.1.41)

∂

∂t

+ v · ∇ +h ∇ · v − λ ∇

T = 0, (5.1.42)

where terms of up to linear order in the gradients of T (r, t) and v(r, t) have been kept in

the dissipative parts of the currents. To close the set of equations we express the ﬂuctuation