Das Sh.P. Statistical Physics of Liquids at Freezing and Beyond

Подождите немного. Документ загружается.

4.3 The landscape paradigm 181

Fig. 4.7 The nucleation time τ

(solid line) and relaxation time τ

(dashed line) in a schematic

model. If the two do not cross (left panel) the liquid can equilibrate without nucleation setting in.

If τ

>τ

at temperature T

nucleation starts before the liquid equilibrates. T

is the kinetic

spinodal. Reproduced from Cavagna et al. (2005).

 American Physical Society.

According to eqn. (4.2.8) the nucleation time τ

increases since the denominator of the

exponent on the RHS is reduced as a result of including the elastic contribution to the free

energy. The above relation has schematically been solved (Cavagna et al., 2005) assuming

that the prefactor τ

is inversely proportional to the shear viscosity and that the Stokes–

Einstein relation continues to hold τ

≈ τ

,theα-relaxation time. In the schematic model,

the likelihood of the curve of the relaxation time τ

crossing that of the nucleation time

and hence the possibility of the spinodal point at an intermediate temperature T

has

been demonstrated. In Fig. 4.7 this scenario of the existence of a kinetic spinodal due to

the viscoelastic contribution to the free energy of the nucleus is shown.

4.3 The landscape paradigm

A useful approach to the study of the complex behavior of a many-particle system has been

studying the multi-dimensional potential-energy landscape or sometimes the so-called free-

energy landscape of a small number of particles. This has been particularly effective in

recent years with the availability of fast computers. The application of energy landscapes

has been a useful method for various disciplines of chemical physics (Wales, 2003) con-

cerning clusters, glassy systems, and proteins. In the present section we mainly focus on

some of the recent results obtained using the landscape paradigm for the structural glasses.

182 The supercooled liquid

4.3.1 The potential-energy landscape

In 1969, in a seminal paper Goldstein presented a picture of the dynamics of a supercooled

liquid that was based on the evolution of the system in the multi-dimensional phase space

of all the conﬁgurational degrees of freedom. In a simple monatomic system of N particles

in three dimensions this refers to a set of 3N coordinates in total. The total potential energy

U (r

) of the system deﬁnes a hypersurface that is often termed the potential-energy land-

scape (PEL). The PEL is characterized by different minima of the potential energy. In the

consideration of the metastable supercooled liquid the lowest minimum, corresponding to

the crystalline state, is ignored. The local minima represent only the amorphous structure

here. The system is represented by a single point moving over the PEL. At a ﬁnite temper-

ature there are ﬂuctuations of the energy, allowing the system to move from one minimum

to another by crossing barriers. For the equilibrium liquid, which is ergodic, these jumps

occur of course between minima that on average have similar energy values. The average

potential energy thus remains constant in time. The PEL is related to the mechanical prop-

erties of the N-particle system and is not dependent on the temperature T which refers to

the thermodynamic state of the system. However, it is important to realize in this respect

that, even though the PEL is not dependent on T , the part of the landscape explored by the

system is strongly linked to the temperature of the system.

The key aspect of the Goldstein picture is that at low temperature the the point rep-

resenting the system remains conﬁned to a local minimum until it moves out by making

activated jumps over potential barriers. Thus the atoms are held in positions correspond-

ing to small (vibrational) motions around a local minimum of the potential energy until

a large enough ﬂuctuation causes the system to jump over the potential barrier to move

to another minimum. There are thus two different time scales characterizing the behavior

of the system in this situation: ﬁrst, vibrations for the system around a local minimum;

and second, the system eventually crossing over from one minimum to another. At high

temperature the thermal energy of the system is very comparable to the height of the barri-

ers between different minima and the activated hopping does not control the dynamics. In

this situation relaxation is fast and the normal ﬂuid dynamics prevails. The above scenario

indicates that with the fall of temperature there is a crossover in the dynamics of the liq-

uid from continuous ﬂuid-type motion to activated barrier hopping over potential barriers.

From qualitative considerations Goldstein estimated that this occurs around a relaxation

time scale of 10

−9

s. This is fast compared with the relaxation times of the order of 10

near T

, but slow compared with the usual relaxation time of the order of 10

−13

s near T

Since the growth of relaxation times is very fast near T

, the above crossover occurs at a

temperature intermediate between T

and T

The activated barrier hopping in the PEL for the supercooled liquid was interpreted by

Goldstein as a rearrangement of particles in a small region of the system in real space.

Such rearrangements can occur independently in different parts of the system at low tem-

perature. The crucial point here is that this activated barrier hopping of the system implies

rearrangement of a number n of the liquid particles which is sub-extensive, i.e., n/N → 0

4.3 The landscape paradigm 183

in the thermodynamic limit. The height of the potential barrier which is to be surmounted

in order to hop from one minimum to another in such a rearrangement is O(n) and is sub-

extensive. Understanding the growth of the barrier height or n in this PEL picture with

increasing supercooling is therefore a key aspect of the theory of vitriﬁcation.

The conﬁgurational entropy S

)

We discuss below a formal way of partitioning the conﬁgurational space as a sum of contri-

butions from distinct basins of the potential-energy landscape. The partition function Z

for a system of N particles is

N !



−βV (r

)

, (4.3.1)

where 

is the thermal de Broglie wavelength and β = 1/(k

T ). Assuming that the

sum in Z

can be partitioned into basins, the integral on the RHS over the conﬁgurational

space is expressed as a sum over individual basins,



−βV (r

)



−βe



∈i

−β

V (r

)

, (4.3.2)

where “∈i” implies that the integral is computed for the i th basin. V (r

) = e

V (r

V represents the vibrational part of the potential energy over the minimum at e

.To

sum the contributions from the different basins we denote the partition function for the

system conﬁned in the basin with an energy e

as Z

, T , V ). This is obtained by

doing a constrained sum in which only the basins with energy e

are counted,

, T , V ) =



(e

)



−βe



∈i

−β

V (r

)

, (4.3.3)

where (e

) =

counts the total number of basins of depth e

. The above def-

inition allows us to formally write the full partition function deﬁned in eqn. (4.3.1) as the

sum over different basin energies e



(e

, T , V ). (4.3.4)

The combinatorial factor of N ! in the denominator of the RHS of eqn. (4.3.1) disappears

since the sum over all distinct basins and permutations of the particles does not change the

basin. We deﬁne a basin free energy f

basin

, T , V ) as

basin

, T , V ) =−k

T ln Z

, T , V ) (4.3.5)

to obtain the result



(e

−β f

basin

,T ,V )

. (4.3.6)

184 The supercooled liquid

The number of local minima in the PEL (e

) corresponding to a given e

deﬁnes the

conﬁgurational entropy S

of the supercooled liquid as

) = k

ln (e

). (4.3.7)

The partition function is written in terms of the basin free energy and the conﬁgurational

entropy as



(e

−β[ f

basin

,T ,V )−TS

)]

. (4.3.8)

The terms in the exponent on the RHS are extensive quantities, i.e., proportional to the

number of particles. Hence, in the thermodynamic limit we evaluate the integral in terms of

the corresponding saddle point at e

=¯e

(T , V ). The latter is obtained from the solution

of the equation at given V and T ,

∂ S

)

∂e

∂ f

basin

)

∂e

. (4.3.9)

The free energy as a function of temperature and volume is obtained in terms of ¯e

F = f

basin

(¯e

) − TS

(¯e

). (4.3.10)

The RHS is the free energy of the liquid constrained to remain in one of its characteris-

tic basins plus an entropic term −TS

) that counts the number of basins explored at

temperature T .

Computer models for supercooled liquids

Computer-simulation methods (Allen and Tildesley, 1987) have generally been extremely

useful for studying the dynamics of supercooled liquids, including nonequilibrium phe-

nomena such as aging. In traditional molecular-dynamics (MD) simulations, the classical

equations of motion for a small number of particles (a few hundred) are solved in the

computer. The maximum time scale over which the particles are simulated in a typical

MD simulation is not comparable to the time scales of glassy relaxation seen in real

experiments. However, MD simulations easily obtain a variety of correlation functions

not accessible to experimental techniques. Real-space correlation functions are as easily

computed as their Fourier-transformed counterparts. The motion of a single particle in the

ﬂuid and its heterogeneous dynamics over different time scales are also easily obtained

in simulations. Monte Carlo (MC) methods in which a physical property of the ﬂuid is

obtained by generating a possible set of conﬁgurations used for ensemble averaging are

also used. The particles interacting through a known potential are assigned an arbitrary set

of coordinates, which evolves through successive random displacements. Here the particle

momenta do not enter into the computation and no time scale is involved (unlike in MD). A

problem often faced in computer simulation of liquids in the supercooled state is that crys-

tallization intervenes. Traditionally nucleation is avoided more easily by studying binary

mixtures of spherical particles of different diameters (Bernu et al., 1985; 1987). As an alter-

native approach, the dynamics of the monatomic system has also been studied (Angelani

4.3 The landscape paradigm 185

et al., 1998) with the master equation for a model system (consisting of a small number of

particles) evolving in the PEL. Crystallization is avoided here by simply ignoring the corre-

sponding minima from the landscape. We list below a few examples of simulated systems

consisting of a small number of particles interacting through a simple interaction potential.

1. A binary mixture of Lennard-Jones (BMLJ) liquids: an 80 :20 mixture of 8000 particles

of two species A and B. The spherically symmetric interaction u

αβ

between two types

of particles α, β ∈{A, B} at a distance r is deﬁned as

αβ

(r) = 4

αβ



(

αβ

)

−

(

αβ

)



, (4.3.11)

with the following choices for 

αβ

and σ

αβ



= 1.0,

= 1.5,

= 0.5,

= 1.0,σ

= 0.8,σ

= 0.88. (4.3.12)

The potential u

αβ

(r) is cut off at r > 2.5σ

αβ

or minor variations of it in different cases.

The AB interaction is stronger (deeper well) than both AA and BB interactions. The

results of the simulation are generally expressed in reduced units: length is scaled with

respect to σ

, temperature in units of 

, and time in units of



mσ

/



1/2

where m is the mass of particles of either species A or species B. This system is usually

termed the Kob–Andersen mixture or BMLJ type I.

2. A 50 : 50 mixture of BMLJ systems with different potential parameters (Sastry et al.,

1998) has been used by various authors. Here all attractive interactions have the same

strength 

= 

and σ

= (σ

+ σ

)/2.WerefertothisasaBMLJ

type-II mixture.

3. A 50 : 50 mixture of soft-sphere particles of species A and B with u

αβ

(r) = 

(σ

αβ

/r)

where α, β ∈{A, B}. Barrat and Latz (1990) simulated this mixture of soft spheres

for studying liquid dynamics in the supercooled state. Yamamoto and Onuki (1998a,

1998b) simulated a soft-sphere mixture with σ

= (σ

+σ

)/2 and the interaction

is truncated at r = 4.5σ

in two dimensions and r = 3σ

in three dimensions. The

ratio of the sigmas is σ

/σ

= 1.4 (1.2) in two (three) dimensions. The mass ratio

of the two species is chosen as m

= 2. For the mixture of soft spheres an effective

diameter is computed as

eff



α,β=1

αβ

, (4.3.13)

where x

= N

/(N

+ N

) for s = 1, 2. The state of the binary mixture is sometimes

characterized by a single parameter 

eff

deﬁned as



eff

= n







d/12

eff

, (4.3.14)

where n

= (N

+ N

)/V is the total number of particles per unit volume.

186 The supercooled liquid

With the availability of modern computers it is possible to calculate the potential-energy

function U(r

) for a system with a large number (though much smaller than that for the

thermodynamic limit) of particles. Stillinger and Weber (Stillinger and Weber, 1982, 1984;

Stillinger 1995) developed a technique for studying the PEL in a systematic manner. The

nature of this hypersurface is analyzed in a statistical way in terms of basic quantities

such as the number of local minima and the density of such minima as a function of the

energy. The shape of the surface near the local minimum and the hypervolume associ-

ated with a minimum are also important ingredients in the PEL approach to the physics

of supercooled liquids. Starting from each point in the conﬁguration space, a steepest-

descent minimization of the potential-energy function is performed until a local minimum

is found. The position of the local minimum in the conﬁguration space deﬁnes an inherent

structure denoted “IS.” The set of all points connected to a given local minimum in the

above procedure deﬁnes a basin for the corresponding IS. Except for a set of points of zero

measure accounting for the saddles and ridges between the different basins, all points in

the conﬁguration space are associated with a corresponding local minimum.

Crossover in the dynamics

Simulation of a Kob–Andersen BMLJ system of 256 particles has been done in order to

analyze (Sastry et al., 1998) the dynamics within the IS structure approach. Three char-

acteristic temperatures were observed by analyzing the nature of the dynamics of the

representative point of the Kob–Andersen BMLJ system of 256 particles on the PEL. First,

for T > T

≈1.0 the average energy ¯e

of the IS for the equilibrium liquid is insensitive

to the temperature T . The corresponding self-intermediate function decays exponentially

with time and the relaxation time grows with temperature in an Arrhenius manner. For

T < T

, the energy corresponding to the IS, ¯e

, falls with temperature. The relaxation is

nonexponential and the temperature dependence of the relaxation time is non-Arrhenius in

this region. Around T

≈ 0.42 there is another crossover in the dynamics. The potential

energy barriers between IS basins increase and the system remains largely in the harmonic

regions of the basins. The dynamics below T

is controlled largely by activated hopping

processes. The temperature range between T

and T

has been called the landscape-

inﬂuenced regime. At a much lower temperature T

the system gets trapped in a single

low-energy basin. For the slowest cooling rate of the system T

≈ 0.25. The temperature

range from T

to T

has been called the landscape-dominated regime. In the landscape-

inﬂuenced regime, as the temperature of the system approaches T

from above the inter-

basin hopping becomes increasingly rare. This temperature marks a clear separation of

time scales between intra-basin dynamics and activated hopping between barriers.

In a related study Schröder et al. (2000) studied the successive conﬁgurations produced

in an MD simulation of a BMLJ type-II mixture containing 251 A particles and 249 B

particles. The successive conﬁgurations of the particles were mapped into a corresponding

time series of local minima (IS). The self-intermediate scattering functions both for the

actual structure (representing the true dynamics) and for the corresponding IS (representing

inherent dynamics) were compared. Beyond a crossover temperature T

(say), it is found

4.3 The landscape paradigm 187

that the inherent dynamics is the same as the true dynamics from which the effects of

vibrations has been removed. Beyond T

the dynamics of the system in the conﬁguration

space consists of its fast vibrational motion (intra-basin) in a local minimum and slow

diffusive motion among different basins. The landscape scenario has been used to study

the thermodynamics of supercooled liquids in a number of works in recent years (Doliwa

and Heuer, 2003; Sciortino, 2005; Heuer, 2008).

Our understanding of the dynamics of the representative point of the system on the PEL

grew clearer as the landscape was studied in terms of local minima as well as the sad-

dles (Angelani et al., 2000; Broderix et al., 2000). The type-I BMLJ system of particles

at ﬁxed density 1.2 was equilibrated at a given temperature T , using standard MD tech-

niques, and the saddle of the PEL U (x) was located by looking for the absolute minima of

W (x) =∇U · ∇U . All the extrema were classiﬁed in terms of their potential energy u and

the number of unstable directions K(u) (number of negative eigenvalues of the Hessian

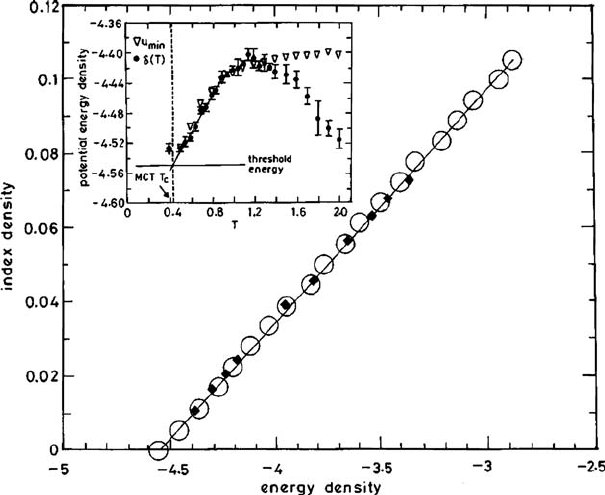
matrix) called the index density, corresponding to the energy u.InFig. 4.8 aplotofthe

index density K(u) vs. the corresponding energy density is shown. The data were obtained

Fig. 4.8 The index density vs. the potential energy. An average over all data was obtained by sam-

pling at T

∗

∈[0.3, 2.0]. The solid line is a linear ﬁt meeting the energy axis at u

. The inset shows

the average density of the local minima u

min

(triangles) as a function of the temperature of the

initial MD trajectory. Circles represent δT , the average potential-energy density U/N(T ) minus

the vibrational energy 3T /2 in the harmonic approximation. The threshold energy u

=−4.55 is

reached at T

∗

= 0.44 ≈T

. Reproduced from Broderix et al. (2000).

 American Physical Society.

188 The supercooled liquid

by (a) averaging the energy for all the extrema (irrespective of the temperature correspond-

ing to the initial conﬁguration) with a given index density (geometric average) and (b), at

a given temperature T , averaging all the energies and the corresponding index densities

(parametric average). The K(u) curve meets the energy axis at a threshold value u

that

marks the border between the saddle-dominated part of PEL and the minima-dominated

part. u

is above the lowest-lying minimum, u

, which is found in the PEL, indicating

the existence of a ﬁnite energy-density interval within which there are overwhelmingly

more minima than saddles. With increasing temperature, u

increases and eventually, at

a critical temperature T

, crosses u

. Thus, for T > T

the representative point of the

system is in the part of the PEL which is dominated by saddles. This temperature T

there-

fore indicates a crossover from nonactivated dynamics (above T

) to activated dynamics

(below T

). The evidence from the landscape studies on model systems strongly suggests

that T

is close to the T

at which the extrapolated self-diffusion coefﬁcient of a parti-

cle in the liquid goes to zero. For the BMLJ system at ρ =1.2 one obtains T

=0.435

(Angelani et al., 2000), or 0.44 (Broderix et al., 2000). Computer simulation (Kob and

Andersen, 1994, 1995a, 1995b) of the same system shows that the self-diffusion coefﬁ-

cient goes to zero with a power law at T

= 0.435 (see Section 8.2.3 in Chapter 8 for more

details). The results from another typical fragile liquid, i.e., soft-sphere, mixture (simu-

lated using MC methods) indicate a similar relation: T

=0.242 ± 0.012 (Grigera et al.,

2002) and the corresponding T

= 0.226 (Roux et al., 1989). We will see in Chapter 8 that

this temperature T

can be identiﬁed with the dynamic transition point of mode-coupling

theory (MCT) in the sense that power-law growth of the relaxation time occurs.

4.3.2 The free-energy landscape

The thermodynamic free energy is a function of temperature and has a characteristic value

corresponding to an equilibrium state. For the study of the glassy state this concept is often

generalized to a coarse-grained Hamiltonian in terms of a set of suitable order parameters.

The most obvious choice of the parameters for the coarse-grained Hamiltonian of a system

with aperiodic density proﬁles is a set of spatial coordinates {R

} that corresponds to the

centers of the inhomogeneous density proﬁles. In other words the {R

} denote the average

positions of the constituent particles in a localized state. Such a parametrization deﬁnes

a multi-dimensional landscape. With the entropic contribution included this is generally

referred to as the free-energy landscape. Such models for supercooled liquids have been

studied by evaluating the free-energy functional for a small number of particles. The size

of the system considered is much smaller than the thermodynamic limit. The spirit of such

models is similar to that of MD simulations with a ﬁnite-sized system.

The optimization of the Ramakrishnan–Yussouff (RY) free-energy functional with

respect to aperiodic density proﬁles was done numerically (Dasgupta, 1992) in the super-

cooled regime. This involved computing the free energy for a small volume L

having

L = 4σ to 6σ , where σ is the hard-sphere diameter with periodic and free boundary

conditions. The volume was divided into a cubic grid with lattice constant a

= 0.2σ ,

4.3 The landscape paradigm 189

using the hard-sphere Percus–Yevick (PY) structure factor in the free-energy functional.

The system underwent the freezing transition to an f.c.c. lattice at a somewhat lower pack-

ing fraction value of 0.43 (the corresponding simulation value is 0.49). The glassy minima

were found to have free energies above that of the f.c.c. crystal and lower than that of the

liquid for packing fractions below the crystallization transition point. The calculation of the

local bond-orientational order parameters (see eqn. (3.4.1) for their deﬁnition) gave values

indicative of local icosahedral order in the metastable glassy state.

A lattice-gas model

The dynamics of the dense ﬂuid in terms of its evolution in the free-energy landscape was

studied by Fuchizaki and Kawasaki (1998) by mapping the problem to a kinetic lattice-

gas-type model. Here density is considered as the only relevant variable and a discretized

version of the Fokker–Planck equation is considered in the form of a mesoscopic kinetic

equation (Kawasaki, 1966a). In the lattice description the system is divided into an assem-

bly of primitive cells with lattice constant h. The dynamics is governed by the following

master equation for the probability distribution P

[n, t] of having density proﬁles denoted

as n at time t:

∂

[n, t]=





(n|n



, t) − w



|n)P

(n, t)

. (4.3.15)

The proﬁle n ≡{n

} denotes a set of occupation numbers with n

=0 or 1 depending on

whether the ith lattice site in the grid is vacant or occupied, respectively. The transition

probability from {n



} to {n} is denoted as w

(n|n



), which satisﬁes the detailed-balance

condition. The energy of the conﬁguration {n} is obtained in terms of the Hamiltonian

[{n

}] = −



i=j

c(|r

− r

|)n

, (4.3.16)

where r

denotes the position vector of the ith site and c(r) is the two-point direct cor-

relation function. Equations (4.3.15) and (4.3.16) for the kinetic Ising model are solved

by the Monte Carlo method to obtain a time sequence of n(t) (Fuchizaki and Kawasaki,

1998). A system of size

L =15 consisting of

lattice points with lattice constant h is

chosen. c(r) is taken from the solution of the PY equation with the hard-sphere diame-

ter as σ =3.3h. The incommensurability of σ/h prevents crystallization setting in. The

occupation number n

(t) in the lattice-gas formulation is related to the local particle den-

sity ρ(r, t) =

δ(r − r

) in the continuum (for convenience we take the particle mass

m = 1) by the relation

n



=ρ(r

, t)

, (4.3.17)

with the time average ...

taken over the typical relaxation time τ . The occupation num-

bers n

in the present context actually refer to entities that are different from a real ﬂuid

particle. On coarse-graining the system over a length 

(say) larger than h, but smaller

than σ , the identity of an individual particle is lost. The master equation (4.3.15) on coarse

190 The supercooled liquid

graining reduces (Fuchizaki and Kawasaki, 1999) to the Fokker–Planck equation (8.1.126)

for a density distribution {ρ

}, where the subscript α corresponds to the αth cell in the

coarse-grained description. Since the PY direct correlation function c(r) is generally nega-

tive, the equations for the dynamics are the same as those corresponding to a spin-one-half

Ising Hamiltonian with anti-ferromagnetic interaction in an external magnetic ﬁeld. The

solution of the master equation (4.3.15) at the initial stage of the dynamics (Fuchizaki and

Kawasaki, 1998) correctly captures the role of the slowly decaying density ﬂuctuations. For

low densities corresponding to packing fraction ϕ ≤0.490 the density correlation func-

tion follows the stretched exponential form exp[−(t/τ

(q))

]. With increasing packing

fraction the stretched exponential relaxation ﬁrst appears at larger wave numbers.

Let us focus on the results obtained for the late stage of the dynamics dominated by

thermally activated transitions between different free-energy minima. For this a reference

state is deﬁned in terms of the state vector

(t)=



i=1

(t)|e

, (4.3.18)

where n

(t) is the occupation variable, which is equal to 0 or 1 depending on whether

the ith lattice site is empty or occupied at time t and |e

=|0 ...0.

.0 ...0 is the ith

orthonormal basis (of size

) in the Fock space. The superscript α refers to a particular

initial state. Now an average state vector is deﬁned as

ref

|¯n

≡



+τ



)

, (4.3.19)

where the origin

of the observation is chosen to be sufﬁciently large to ensure equilibra-

tion. The duration τ is much longer than the microscopic time scale (phonon characteristic

time) but shorter than the time scale of thermally activated jumps. N

is the norm of the

state |¯n

, so that N

1/2

≥N

≥ N /(

3/2

, N being the number of particles in the ﬂuid.

The ﬁrst equality holds when the system is completely frozen during the time interval over

which the average is taken, while the second one holds when the occupied sites are uni-

formly distributed. The state of the system at some later time t is denoted by

with the

averaging process done as deﬁned in (4.3.19). In order to study how the system explores

the free-energy landscape, an overlap function q(t) is considered,

q(t) =

ref

. (4.3.20)

The time scale over which correlation is studied extends from t to t +τ

, τ

being the time

scale of decay of density ﬂuctuations. The result is shown in Fig. 4.9 for three packing

fractions, ϕ = 0.312, 0.440, and 0.491. For ϕ =0.312, q(t) is almost time-independent

(close to unity) since

is independent of t and is essentially the same as

ref

.This

indicates that the system stays around a single global liquid-state minimum. As the system

becomes more dense, ϕ = 0.440, beyond the equilibrium crystallization packing fraction

of ϕ = 0.430, the amplitude of ﬂuctuation of q(t ) increases but the system is still trapped