Das Sh.P. Statistical Physics of Liquids at Freezing and Beyond

Подождите немного. Документ загружается.

3.4 Computer-simulation studies 151

For characterization of the solid-like phase being formed in the liquid an unambiguous

numerical criterion needs to be speciﬁed. For analyzing the nature of a crystal structure

various methods have been developed (Mandell et al., 1976; Honeycutt and Andersen,

1984; Yang et al., 1990). A widely used approach is the analysis of the Voronoi polyhedron

(VP) (Ashcroft and Mermin, 1976) associated with a given particle in the crystal. This

polyhedron for a particle is the set of all points of space that are closer to it than to any other

particle. It is customary to represent the VP for a given crystalline structure in terms of a set

of numbers {n

}≡(n

, n

,...)called signatures. n

represents the number of faces of

the polyhedron with l sides. For a perfect crystal the VP is the corresponding Wigner–Seitz

cell (Wigner and Seitz, 1933). Thus a perfect b.c.c. structure is represented by signatures

(0, 6, 0, 8, 0,...) representing six squares and eight hexagons. At ﬁnite temperature this

representation will be modiﬁed by thermal vibrations. As a consequence a given crystal

structure is described by a distribution of signatures of the corresponding VPs. A similar

description can be constructed in terms of a suitable order parameter for the problem and

will be considered in the present context.

Liquid and solid-like clusters

We describe below the scheme developed by Frenkel and coworkers (ten Wolde et al.,

1996) for studying nucleation phenomena with computer simulations. This method uses the

deﬁnition of a liquid-state order parameter by Steinhard et al. (1983). The main advantage

of this scheme lies in the fact that it identiﬁes the solid-like clusters from the disordered

liquid state and is rather insensitive to the type of the speciﬁc crystalline order. In the

metastable liquid undercooled below its freezing point the embryo of the crystal forming

in the melt consists of particles (solid-like) that are in an environment qualitatively different

from that of the particles in the melt (liquid-like). In order to classify the different particles

of the system evolving during the simulation process as being solid-like or liquid-like, a

local criterion is developed in terms of the local orientational order parameter ¯q

(i).The

order parameter is deﬁned as follows.

We consider a set of neighbors N

(i) of the particle i consisting of all the particles which

lie within a radius of, say, r

around it. The unit vector

along r

depends on the polar

and azimuthal angles, denoted by θ

and φ

, respectively. The local orientational order

parameter is deﬁned in terms of spherical harmonics as

(i) =

(i)



j=1

(

). (3.4.1)

Using the above deﬁnition of the local order parameters, we average over all particles to

obtain the global order parameter Q



i=1

(i)q

(i), (3.4.2)

152 Crystal nucleation

with the normalization factor N being equal to

(i) summed over all the particles i

in the system. From Q

a rotationally invariant form of the order parameter is obtained as



4π

2l + 1



m=−l



1/2

. (3.4.3)

Owing to the presence of the sharp cutoff r

the spatial derivative of the order parameter

is not smooth and hence one must introduce suitable smoothing functions (ten Wolde

et al., 1996). For studying the nucleation phenomena it is convenient to deﬁne for the

many-particle system a suitable quantity that measures the degree of long-range order as

it changes from the disordered liquid to the ordered crystalline state. The quantity Q

for l =6) deﬁned as above has the desirable property that it vanishes in the bulk liquid

and acquires values O(1) for simple crystal lattices. Additionally, its value is insensitive to

any speciﬁc type of crystal symmetry. Another suitable reaction coordinate for the nucleus

is the number of particles n in a given cluster. The free-energy barrier for the cluster is

obtained as a function of the reaction coordinate.

In order to analyze the structure of the nucleus a local order parameter q

(i) (similar to

the global quantity Q

) is deﬁned at the individual particle level,

(i) =



4π

2l + 1



m=−l

(i)|



1/2

, (3.4.4)

representing the extent of local order around i . Focusing on the l =6 case, corresponding

to the particle i a normalized ((2 ×6) + 1)-dimensional vector

O is deﬁned with properly

normalized components such that

O(i) ·

O(i) =1. Using this deﬁnition of the local order-

parameter vectors, two particles i and j are treated as being “connected” if the dot product

of the corresponding

O vectors exceeds a certain threshold value, say 0.5 (ten Wolde et al.,

1996). In order to classify a solid-like particle, it is checked whether the number of its

neighbors to which it is “connected” exceeds a certain threshold value. In Fig. 3.10 we

show in a Lennard-Jones system at coexistence (P =5.68 and T =1.15) the distribution of

the number of connections per particle corresponding to the thermally equilibrated liquid,

f.c.c., and b.c.c. structures. From Fig. 3.10 the usefulness of the above criteria in identifying

solid-like particles is clear. If we take a threshold value of seven connected neighbors to

characterize a particle as solid-like, then 99% of the particles in the f.c.c. structure and 97%

of the particles in the b.c.c. structure are solid-like. On the other hand, for the liquid state

less than 1% of the particles are solid-like.

3.4.1 Comparisons with CNT predictions

The formation of the critical nucleus is studied with a biased Monte Carlo method (van

Duijneveldt and Frenkel, 1992; ten Wolde et al., 1996) with the cluster size or the number

3.4 Computer-simulation studies 153

Fig. 3.10 In a Lennard-Jones system at coexistence (P =5.68 and T =1.15) the distribution of the

numbers of connections per particle (see the text) corresponding to the thermally equilibrated liquid,

f.c.c., and b.c.c. structures are shown. The distributions are based on averages over 50 independent

atomic conﬁgurations. From ten Wolde et al. (1996).

 American Institute of Physics.

of particles n in it as a reaction coordinate for the nucleation process. The probability

P(n) for its formation is computed to obtain the Gibbs free energy using the relation

G(n) = G

− k

T ln[P(n)], (3.4.5)

where G

is a constant. In order to obtain reliable results for all n values, an umbrella

sampling technique (Torrie and Valleau, 1974) was adopted for sampling the conﬁgura-

tion space. This involved using the biased Monte Carlo technique to sample a part of

the conﬁguration that would have been inaccessible in direct simulations. The simula-

tions were carried out at constant temperature and pressure. In Fig. 3.11 the values of the

Gibbs free energy of a hard-sphere system compressed to P =15, 16, and 17 at volume

fractions ϕ ≡ ϕ

liq

=0.5207, 0.5277, and 0.5343, respectively, are shown. These packing

fractions correspond to a relatively low range of super-saturations and the pressures used

in the simulation are all higher than the coexistence value P

coex

=11.67. The maximum in

the plot of the Gibbs free energy against the number of particles in the cluster represents

the critical nucleus and gives the corresponding free-energy barrier. Compared with the

experimental data from crystallization of liquids (colloidal systems) the simulation results

are low by approximately a factor of 3 (Schätzel and Ackerson, 1993; Harland and Van

Megen, 1997). The corresponding quantities as predicted from the CNT in eqn. (3.1.50)

are obtained using phenomenological estimates of the speciﬁc volume v

and chemical

potential difference μ for pressure P of the hard-sphere system (Hall, 1970). Using the

surface tension γ

as a free parameter the simulation data ﬁt to the CNT predictions as

shown in Fig. 3.11 and the best-ﬁt estimate for γ

differs from its value at the coexistence

pressure obtained through independent simulation studies. However, if the above best-ﬁt

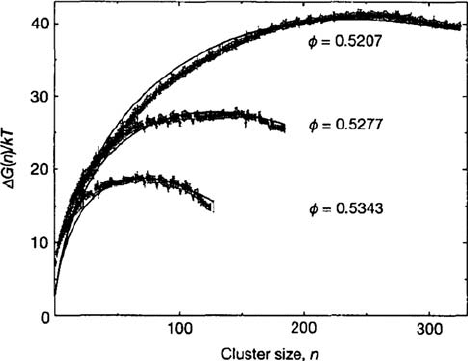
154 Crystal nucleation

Fig. 3.11 The free-energy barrier G(n) (in units of k

T ) to homogeneous crystal nucleation in

a hard-sphere model of colloids vs. the number of particles in the largest solid-like cluster in the

system. Results for the barrier computed using (3.4.5) are shown for three volume fractions ϕ

liq

denoted as φ =0.5207, 0.5277, and 0.5343, corresponding to pressures P =15, 16, and 17, respec-

tively. See also the schematic drawing of Fig. 3.1. The curves drawn are ﬁts to the CNT expression

(3.1.9) using the capillary approximation. The ﬁts obtained for the surface tension γ give the values

(P =15) =0.699, γ

(P =16) =0.738, and γ

(P =17) =0.748. From Auer and Frenkel (2001).

 Nature Publishing Group.

results obtained for γ

from the simulations at various pressures are linearly extrapolated

to the coexistence pressure, the agreement is good. This conforms to the usual criticism of

the CNT, namely that it underestimates the free-energy barrier since it uses the value of the

surface tension at the coexistence pressure.

For the Lennard-Jones system the free-energy barrier to the nucleation is computed

by using similar techniques to those mentioned above. In what follows we represent the

temperature and pressure of the Lennard-Jones system in reduced units (see Chapter 1).

A convenient way of identifying the critical nucleus is to plot the dependence of the

Gibbs free energy on the reaction coordinate Q

to locate the maximum barrier height.

For small values of Q

, corresponding to the liquid state, the solid-like clusters have

few particles. At this stage of the simulation several small clusters are formed, signify-

ing that it is entropically favorable to distribute a given amount of crystalline phase in

several units. As the top of the barrier is approached, the surface energy dominates and

the small solid-like clusters merge, forming a bigger cluster, which is the critical nucleus.

The simulations are performed (ten Wolde et al., 1996) at two reduced pressures, P =0.67

and P =5.68, which correspond to the transition points of T =0.75 and T =1.15, respec-

tively. The temperatures are kept at 20% undercooling from the respective transition points,

i.e., at T =0.60 and T =0.92. The barrier height studied as a function of the reaction

coordinate Q

displays a maximum for the corresponding critical nucleus. According to

3.4 Computer-simulation studies 155

the CNT the free-energy barrier height corresponding to the critical nucleus is given by

(3.1.50). Using results from independent simulation data on Lennard-Jones systems near

freezing for the enthalpy change (Hansen and Verlet, 1969) and the average surface free

energy γ

(Broughton and Gilmer, 1986), the CNT prediction for the barrier height is com-

puted. This procedure leads to G/(k

T ) =17.4 and 8.2 for pressures P =0.67 and 5.68,

respectively. The results from simulations done at those two pressure values are given by

G/(k

T ) ≈ 19.4 and G/k

T ≈ 25.1, respectively. Clearly the agreement between

the CNT prediction and the simulation is much better at P = 0.67 than at P = 5.68.

This is somewhat expected since the simulation value of γ

(Broughton and Gilmer, 1986)

used in evaluating the formula of the CNT predictions was obtained at a pressure closer to

P =0.67. The discrepancy between the corresponding CNT result and that of the simula-

tion at the higher pressure P =5.68 is often ascribed to the fact that the surface free energy

should be higher in this case. In fact, an increase of approximately 45% in γ

will make

the two results agree. More recently it has also been argued (Trudu et al., 2006) that the

CNT predictions can be brought closer to the simulation data under such conditions by

taking into account the fact that the critical nucleus is not exactly spherical.

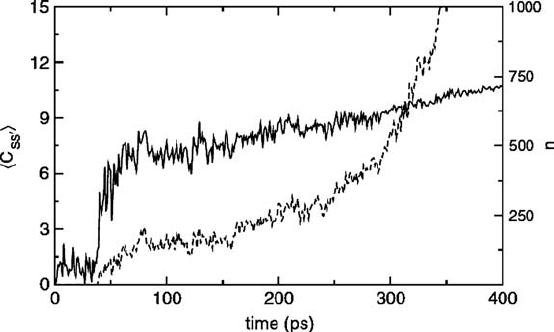
In a recent simulation of the Lennard-Jones system with techniques outlined above

Trudu et al. (2006) studied the crystallization process from the stage of a small embryo

to the critical stage. Here the following criteria were adopted: two particles are considered

as neighbors if their separation is less than r

min

, a distance equal to the position of the ﬁrst

minimum of the radial distribution function. For a solid-like particle (s) in the nucleus C



is the number of its neighbors (s



) that are also solid-like particles. In the liquid phase on

average C



is close to zero until the formation of the embryo with a small number of par-

ticles occurs. This is signalled by an abrupt jump in C



, which takes place at a stage much

earlier than that at which the critical nucleus is reached. This is shown in Fig. 3.12 with

the dashed line. On the other hand, the average number of particles in the nucleus keeps

steadily increasing and would not register this stage in which the coordination number

jumps. Thus at moderate supercooling the crystallization is a two-step process, involving a

precritical embryo followed by a slower growth to the critical nucleus.

3.4.2 The structure of the nucleus

Once the solid-like particles in the undercooled melt have been identiﬁed using the criteria

described above, the crystallites formed by them are determined with the standard cluster

analysis. A typical scheme is to adopt the notion that two solid-like particles that are neigh-

bors belong to the same cluster. It is useful to note that, according to the above deﬁnitions,

every crystal structure formed in the melt is characterized by its own unique distribution

of the value of the local bond-orientational order parameter q

(i) which was introduced

above in eqn. (3.4.4). This distribution is determined by constructing a histogram of the

distribution functions of the bond-order parameter values of the particles corresponding to

a given nucleus. From this histogram we construct a vector ˆv that has as many compo-

nents as the number of bins in the histogram. For example, for a perfect crystal the local

156 Crystal nucleation

Fig. 3.12 The formation of an embryo in the melt, showing the time evolution of the average

coordination number C



between solid-like particles at T/T

=0.8 (solid line) and the number

of solid-like particles in the largest cluster (dashed line). From Trudu et al. (2006).

 American

Physical Society.

bond-order parameter q

(i) is the same for all particles and the histogram has contributions

in a single bin. In general the vector ˆv for a given cluster obtained in the simulation is then

identiﬁed as a linear combination of the corresponding “basic” vectors which represent

the equilibrated liquid, b.c.c., and f.c.c. structures in the same description. The appropriate

values for these coefﬁcients are obtained by minimizing



v −{f

liq

+ f

bcc

+ f

fcc

}

, (3.4.6)

where

bcc

is the vector associated with the histogram of the b.c.c. structure and so on. The

coefﬁcients f

liq

, f

bcc

, and f

fcc

of the basic vectors in this expansion then respectively rep-

resent the relative abundance of the corresponding lattice symmetry in the given structure.

For the Lennard-Jones system at 20% undercooling at T =0.92 and pressure P =5.68 the

structural composition of the largest cluster has been identiﬁed in terms of f

liq

, f

bcc

, and

fcc

. The amplitudes for the different structures are plotted in Fig. 3.13 with respect to the

corresponding value of the reaction coordinate Q

. For small values of Q

, corresponding

to precritical nuclei, the structure is predominantly “liquid-like” and has b.c.c. character.

These nuclei are clearly more b.c.c. ordered than f.c.c. This result of the simulation is

indicative of the Ostwald (1897) “step rule,” which states that crystallization from the melt

takes place by transforming to the phase which is closest in free energy to the liquid state.

Alexander and McTague (1978) extended the Landau theory, arguing from general sym-

metry considerations that in three dimensions for simple liquids freezing into the b.c.c.

crystal phase is favored. For Q

values corresponding to the top of the free-energy bar-

rier Fig. 3.13 shows that the nucleus has predominantly f.c.c. character, which is also in

agreement with the simulations of Swope and Andersen (1990).

3.4 Computer-simulation studies 157

0.005

0.0

1.0

0.8

f, Δ

fcc

bcc

liq

0.6

0.4

0.2

0.015 0.025

0.035 0.045

Fig. 3.13 The structural composition of the largest cluster in terms of f

liq

, f

bcc

, f

fcc

,and

dis-

played as a function of Q

at 20% undercooling, pressure P = 5.68, and temperature T = 0.92.

This is based on 50 independent atomic conﬁgurations. From ten Wolde et al. (1996).

 American

Physical Society.

Assuming the shape of the nucleus to be spherical, the above analysis is extended to

study the nature of its crystallinity as a function of the distance from the center of the

nucleus. The amplitudes f

liq

, f

bcc

, and f

fcc

are computed for a spherical shell of radius r

and shown in Fig. 3.14. The core of the nucleus has mostly f.c.c. structure while in the liq-

uid f

fcc

and f

liq

smoothly go to 0 and 1, respectively. The crystal–melt interface is rather

broad, approximately 4σ , which is similar to what follows from the density-functional

models discussed above and in contrast with the sharp-interface model of the CNT. Also

the plot of the density in the different concentric shells as well as the coordination num-

ber C



deﬁned above against distance indicates a broad interface as shown in Fig. 3.15.

The density falls more sharply over the interface than does the structural order parame-

ter – which is also in agreement with the predictions of the density-functional models (see

Figs. 3.5 and 3.6). The amplitude f

bcc

exhibits a sharp increase near the interface, indicat-

ing its predominantly b.c.c. symmetry. Thus the simulation results indicate that the f.c.c.

core of the critical nucleus is wetted by a shell having a more b.c.c. character. Indeed,

such a behavior is also obtained from the density-functional model, as we have already

discussed above (see Fig. 3.9).

A similar analysis of the structure of the nuclei obtained in simulations of the hard-

sphere system at pressures P =15, 16, and 17 above the coexistence value P

coex

=11.67

has also been done by Auer and Frenkel (2001). The results obtained in this case are

qualitatively different from those for the Lennard-Jones system described above. Analysis

158 Crystal nucleation

0.0

1.0

0.8

f, Δ

0.6

0.4

0.2

1.0 3.0 5.0

7.0 9.0

fcc

bcc

liq

Fig. 3.14 The structure of the critical nucleus, indicated by f

liq

, f

bcc

, f

fcc

,and

, as a function

of the distance r to the center of mass, at 20% undercooling, pressure P =5.68, and temperature

T =0.92. This is based on 50 independent atomic conﬁgurations. From ten Wolde et al. (1996).

 American Physical Society.

1.04

1.02

density

NCP

1.00

0.98

1.0 3.0 5.0 7.0

CNT

9.0

3.0

5.0

7.0

NCP

9.0

11.0

Fig. 3.15 The density and number of connections per particle (NCP) given by C



(see the text)

as a function of the distance r to the center of mass, at 20% undercooling, pressure P =5.68, and

temperature T =0.92. The vertical coordinate axes for density (left) and NCP (right) are chosen over

a range that covers the liquid up to the bulk-solid value in each case. From ten Wolde et al. (1995).

 American Physical Society.

3.4 Computer-simulation studies 159

of the largest cluster formed in the simulation of the hard-sphere system shows that at the

precritical stage the nucleus with a small number of particles has some liquid-like or b.c.c.

structure while the random hexagonal close-packed (r.h.c.p.) structure (Sadoc and Mosseri,

1999; Nelson, 2002) is dominant for larger clusters. Thus, unlike for the Lennard-Jones liq-

uid, the simple b.c.c. structure is not favored in the hard-sphere system during the ﬁrst stage

of crystallization. It nucleates into the metastable r.h.c.p. structure, which at a later stage

transforms into a stable f.c.c. structure.

While the simulation results are in quite good agreement with theoretical predictions for

equilibrium structures, the situation is far less convincing in the case of the nucleation rate.

Using the result (3.1.52), the nucleation rate is given by

J = J

−G

∗

/(k

T )

, (3.4.7)

where the prefactor J

= ZA(T ) is a product of two terms, namely (a) the Zel’dovich

factor Z given in (3.1.39) and (b) a kinetic prefactor A(T ), which is determined by the

frequency ν

exp

− f

∗

/(k

T )

of attachment of a monomer to the nucleus. The latter is

approximated as the inverse of the time taken by a particle to traverse the average inter-

particle distance l

(say). Assuming the Einstein relation of root-mean-square displacement

in diffusive motion, this inverse time is given by 6D

, where D

is the self-diffusion

coefﬁcient. D

is obtained directly through simulation. On approximating l

∼ N

−1/3

the prefactor A is obtained while the Zel’dovich factor Z is computed from the formula

(3.1.40). The nucleation rate is directly estimated from simulation (ten Wolde et al., 1996)

and, by dividing it by the factor exp

− f

∗

/(k

T )

as obtained in the CNT, the prefactor

can be estimated. The value of J

obtained in this way exhibits a discrepancy of two

orders of magnitude from the corresponding simulation results.

Appendix to Chapter 3

A3.1 The schematic model for nucleation

We present below the calculation of the order-parameter proﬁles and the free-energy barrier

for the critical nucleus in the schematic nonclassical model presented in Section 3.2.

A3.1.1 Critical nucleus

Equations (3.2.10) and (3.2.11) are solved in terms of the Yukawa function Y(r) =

exp(±αr)/r, which satisﬁes the equation



≡ α

Y. (A3.1.1)

The boundary conditions of ψ are obtained using the constraints that, for r →∞, ψ → 0

representing the liquid minimum, and dψ/dr → 0asr →0, signifying that the nucleus

at the center has ψ resembling the bulk-crystalline value. Thus eqns. (3.2.10) and (3.2.11)

have respective solutions of the following forms which are valid in two different regimes

controlled by the two free-energy minima at ψ = 0 and ψ = ψ

ψ(r) − ψ

− e

−r

, for small r, (A3.1.2)

ψ(r) =

−¯νr

, for large r. (A3.1.3)

Since the crossover of the free energy is marked by ψ = ψ

, it is plausible that the above

two solutions (A3.1.2) and (A3.1.3) should match at this value ψ

. Let this crossover hap-

pen at r = r

, which is used to evaluate the constants A

and B

, leading to the following

solutions in the two respective regimes:

(r) − ψ

− ψ

r/r



− e

−r

− e

−r



, for r < r

, (A3.1.4)

out

(r) =

r/r

−¯ν(r−r

)

, for r > r

. (A3.1.5)

160