Das Sh.P. Statistical Physics of Liquids at Freezing and Beyond

Подождите немного. Документ загружается.

4.1 The liquid–glass transition 171

A useful quantity in this description is the probability of having an amount of free vol-

ume v

per particle on average. This can easily be calculated assuming the distribution

of this volume to be totally random. Let v

be the free volume associated with N

ﬂuid

particles, then for a total of N particles we have the average free volume v

given by



= N, (4.1.8)



= Nv

, (4.1.9)

where γ is a geometric factor that corrects for the overlap of the free volumes. Note that the

choice of γ as a single constant factor is a gross simpliﬁcation of the situation of complex

dynamics of a strongly interacting many-particle system. The number of different ways in

which the free volumes can be distributed is given by the simple combinatorial factor

 =

N !

. (4.1.10)

By maximizing  for the equilibrium distribution subject to the above two constraints

(4.1.8) and (4.1.9), we obtain the probability of having free volume v and v + dv (treated

as a continuous variable) is obtained as

p(v)dv =

exp



−

γv



dv, (4.1.11)

where the constants on the RHS are chosen so that the probability p(v) is normalized

and the average of the free volume is v

. The above form for the probability (4.1.11) is a

consequence of the random nature of the free-volume distribution in the dense liquid.

4.1.3 Self-diffusion and the Stokes–Einstein relation

The above-described free-volume picture of the supercooled liquid is useful, albeit in

a merely phenomenological way, for modeling the transport process in a dense liquid

(Spaepen, 1977). At the microscopic level, a ﬂow occurs in a dense ﬂuid as a result of

a number of individual atomic jumps. This process can be described using the following

simple picture. Around a ﬂuid particle a cage of volume v

is formed by the nearest neigh-

bors. When a large enough hole occurs, allowing the particle to pass on, a jump occurs. In

modeling this jump process we assume that the positions of the particle before and after

the jump are positions of relative stability and represented by local free-energy minima for

the particle. Let the activation energy or the height of the barrier required to be crossed

be G

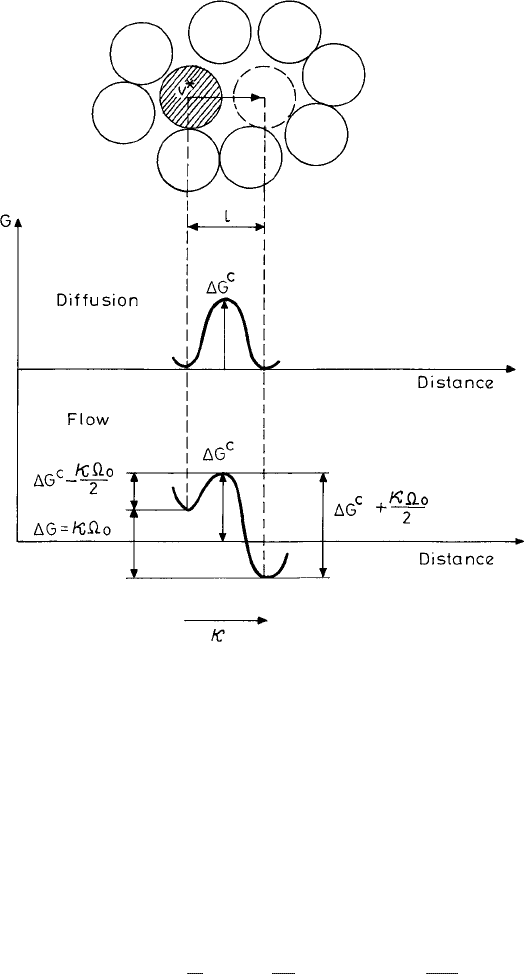
. This is shown by the diagram of a simple two-level system in Fig. 4.4.Inthe

absence of an external force this energy is obtained from thermal ﬂuctuations and hence

equally many jumps occur in the two directions. In this case a tagged particle is undergo-

ing diffusive motion. If, on the other hand, an external force like a shear is applied then

the jumps in the direction of the shear (we call it the forward direction) are favored and

172 The supercooled liquid

Fig. 4.4 The two-level system, showing transport in a dense liquid. The nature of the free-energy

barrier for a ﬂuid particle (shown by the shaded disk) for transport to the position shown by the

dashed circle in two situations, namely by diffusion (upper panel) and in ﬂow in the presence of a

shear (lower panel). Reproduced with kind permission from Spaepen (1977). Reprinted from Acta

Metallurgica with permission from Elsevier.

the two-level free-energy curve for ﬂow is biased in the way shown in Fig. 4.4. As a result

there is a net forward ﬂux of atoms, resulting in a ﬂow. For a quantitative estimate of this

process we need to take into account two factors.

First, if the free volume available is greater than v

, the probability of a jump from a site

occurring is obtained, by integrating eqn. (4.1.11),as



∞

p(v)dv =



∞

exp



−

γv



dv = exp



−

γv



, (4.1.12)

assuming the ﬂow to be homogeneous, i.e., every site is taking part in the ﬂow uniformly.

Second, in the presence of an external shear κ (say) the net number of forward jumps is

obtained using rate theory. The force on an atom is κα

, where α

is the projected area for

4.1 The liquid–glass transition 173

the particle on the shear plane. If the atom makes a jump of length l the work done is κα

Since l is roughly of the same magnitude as the atomic diameter we can take α

l ∼ 

,the

volume of the atom. Therefore the work done is κ

. If in the absence of the shear the free

energies of the two states, before and after the jump, were the same, then in the presence

of the shear they differ by an amount κ

as shown in Fig. 4.4. Therefore the net number

of jumps in the forward direction over the barrier of height G

− κ

/2 is obtained as

ν = ν



exp



−

G

− κ



− exp



−

G

+ κ



, (4.1.13)

where ν

is the atomic vibration frequency. Now, if all the particles in the specimen make a

forward jump of length one atomic diameter, a uniform shear κ = 1 occurs in the system.

If just some of the atoms jump, then the shear rate is equal to the net number of forward

jumps per second. From the above estimation, therefore, the shear rate

ϑ is obtained as

ϑ = S



exp



−

G

− κ



− exp



−

G

+ κ



= 2ν

exp



−

γv



sinh



κ



exp



−

G



. (4.1.14)

For low shear rate κ we assume κ

 2k

T , such that sinh[κ

/(2k

T )]≈κ

(2k

T ). The shear viscosity η is therefore obtained as the ratio of the applied stress κ and

shear rate

ϑ as

η =



exp



γv



exp



G



. (4.1.15)

In the case of diffusion of the particle in a ﬂuid without any shear, the particle is undergoing

a random motion. Hence the states before and after the jump have the same free energy as

shown in Fig. 4.4 and the number of jumps per second (in either direction) from the above

analysis is obtained as

= ν

exp



−

γv



exp



−

G



. (4.1.16)

The diffusion coefﬁcient D

is related to the mean-square displacement d

(t), per unit

time by d

(t)=6D

. Assuming that each of the jumps has an average length l and that

jumps occur with a frequency ν

per second, this relation reduces to

= 6D

. (4.1.17)

Using the expression (4.1.16) for ν

, we obtain the diffusion coefﬁcient for the tagged

particle in a sea of identical particles as

exp



−

γv



exp



−

G



. (4.1.18)

174 The supercooled liquid

From eqns. (4.1.15) and (4.1.18) we obtain the relation

η =

6

, (4.1.19)

where 

is an atomic length. Equation (4.1.19) is the Stokes–Einstein relation for a liq-

uid of identical particles. Note that we have obtained the relation given in eqn. (1.4.28) for

the massive Brownian particle in a surrounding liquid of smaller particles. The above anal-

ysis demonstrates in a phenomenological manner that the same result holds for a liquid of

identical particles. As we discuss in Section 5.2.2, with a model of the liquid that takes into

account only short-time collisions in the transport behavior (the Enskog theory) no such

relation holds. The above analysis applies only for a dense liquid. In the deeply supercooled

state the above relation often breaks down due to decoupling of the rotational and transla-

tional motion of the ﬂuid particle. A microscopic-level explanation of Stokes–Einstein-law

violation in the dense liquid attributes it to the existence of spatial domains with different

rates of atomic mobilities in this state. The translational diffusion is mostly conﬁned to

the fast domains, while the structural relaxation and hence viscosity is controlled by the

reduced mobility in the slow domains (Stillinger and Hodgdon, 1994).

The idea of free volume described above was used by Cohen and Turnbull (1959) and

Turnbull and Cohen (1961, 1970) to model the liquid–glass transition as a thermody-

namic phase transition. Subsequently Cohen and Grest (1979) and Grest and Cohen (1981)

extended the free-volume picture to formulate the thermodynamics of the supercooled liq-

uid. A phenomenological form of the free energy of the supercooled liquid (Debenedetti,

1997) was proposed using the ideal of a cell constituting a molecule and its surrounding

cage. In the Cohen–Grest phenomenological picture cells with volume v>v

are termed

liquid-like whereas those with v<v

are called solid-like. The excess amount v

= v −v

is the free volume associated with a liquid-like cell. Free exchange of free volume can

occur from one liquid-like cell to another when the number of liquid-like cells neighbor-

ing the former exceeds a threshold value z

∗

. Such a combination of liquid-like cells is

termed a liquid-like cluster. In the Cohen–Grest theory the glass transition is viewed as a

dynamic percolation transition in this system. This occurs when the fraction of liquid-like

cells drops below a critical value, causing the clusters to be isolated from one another.

The phase above the percolation transition corresponds to the liquid state with an inﬁnite

liquid-like cluster. The theory describes the liquid–glass transition as an underlying ﬁrst-

order transition that is masked by the system falling out of equilibrium at an earlier stage

due to growing relaxation times. It provides detailed predictions for such as the thermody-

namic quantities discontinuity of the speciﬁc heat and thermal expansion. For example, the

temperature dependence of the viscosity η is expressed as

log

η = C

T − T

+{(T − T

)

+ 4v

T }

1/2

. (4.1.20)

The formula is arrived at with the use of a phenomenological expression (involving

adjustable parameters) for the free energy of the supercooled liquid in terms of free

4.2 Glass formation vs. crystallization 175

volumes associated with the liquid-like and solid-like cells (Grest and Cohen, 1981). The

above formula with a large number of adjustable parameters (C

, D

,ζ

, and T

)

has served as a useful tool for ﬁtting experimental data on viscosity over 14 orders of

magnitude. Molecular-dynamics simulations with simple liquids have also been used to

study the free-volume model (Hiwatari, 1982).

4.2 Glass formation vs. crystallization

The ease of glass formation in a given material depends on the likelihood of avoiding

the onset of crystallization in the supercooled liquid. We now consider the conditions

which control this process in the supercooled liquid approaching vitriﬁcation. Crystal for-

mation from the melt takes place through the nucleation process in which a nucleus of

the crystalline phase grows at the expense of adjacent liquid. We consider only homoge-

neous nucleation here. In Section 3.1.2, we discussed the dependence of the nucleation

rate on the extent of undercooling. The prefactor J

of the nucleation rate was linked

there to the viscosity η of the undercooled liquid using the Stokes–Einstein relation and

the role of the temperature dependence of the shear viscosity η was ignored. The sharp

enhancement of the viscosity of the supercooled liquid with lowering of the temperature,

however, has important implications relating to the prefactor J

. The exponential factor

exp[−f

∗

/(k

T )]in (3.1.52) for J

becomes important near T

. On approaching the tran-

sition the energy barrier  f

∗

grows substantially, making the time τ

taken by a monomer

to cross the interface and become attached to a nucleus very long. This crossover time is

inversely proportional to the self-diffusion coefﬁcient D

of the monomer. Assuming the

Stokes–Einstein relation to hold, τ

grows linearly with η. Hence the prefactor J

in eqn.

(3.1.54) for the nucleation rate is inversely proportional to η. Near T

the time τ

is ﬁnite

but the barrier to nucleation G

∗

is very high and hence, from (3.1.56), it follows that

the nucleation rate J is very low. For low temperatures distant from T

the barrier is low

but τ

grows very fast due to a sharp fall in the self-diffusion coefﬁcient and makes J very

low. Thus, at an intermediate temperature J develops a maximum. This maximum sets the

value of the minimum cooling rate since only if the sample is cooled at a faster rate does

crystallization not intervene.

To see this in more detail, let us assume here that the temperature dependence of η fol-

lows the Vogel–Fulcher temperature dependence (4.1.5). Let the temperatures be expressed

relative to the freezing temperature T

, i.e., T

= T /T

and T

= T

.InFig. 4.5

the dependence of the nucleation rate J on the scaled temperature T

= T /T

is dis-

played using the the constants η

= 10

−3.3

P and E

= 3.34 in eqn. (4.1.5). All other

parameters are kept the same as in Fig. 3.3. All of the curves displayed in Fig. 4.5 corre-

spond to 

= 0.5(seeFig. 3.3 for the deﬁnition of 

). The variation of the nucleation

rate over different stages of the undercooling is therefore strongly dependent on the value

of T

characteristic of the different glass-forming materials (Binder and Kob, 2005). For

higher T

the nucleation rate J changes more sharply and does so over a temperature

range closer to T

. The value of the nucleation rate J also decreases with increasing T

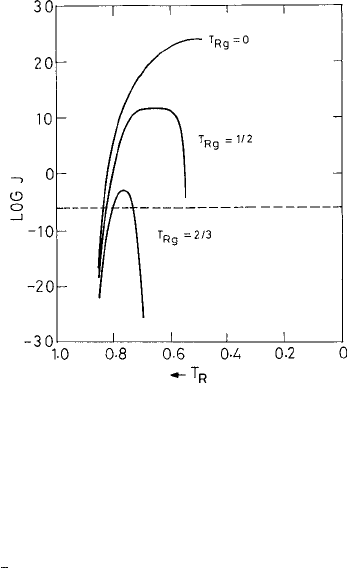
176 The supercooled liquid

Fig. 4.5 The logarithm of the rate J (in cm

−3

−1

) of homogeneous nucleation in the undercooled

liquid vs. the reduced temperature T

= T/ T

for 

= 0.5(seeFig. 3.3). The temperature depen-

dence of the viscosity η present in the prefactor J

in (3.1.52) is taken here in the Vogel–Fulcher

form (see the text) with the parameter T

≈ T

= T

.FromTurnbull (1969).

 Taylor &

Francis Group, http://www.informaworld.com

For example, at T

≈

the nucleation rate is above the threshold value (see Fig. 4.5) only

within a narrow temperature window in the supercooled region, 0.75 < T

< 0.80. On the

other hand, for T

≈ 0.5 the crystallization rate is much higher, opening up a wider tem-

perature window in the supercooled region within which crystallization is likely to occur.

For materials in which the glass-transition temperature T

is closer to T

≈T

∼1),

the temperature window within which nucleation is likely to start in the undercooled liquid

becomes narrower. Hence the tendency toward glass formation grows as T

approaches T

However, once crystallization has started, the liquid is warmed by the latent heat released

in the crystallization process of the rapidly growing crystal and freezing continues up to

a temperature slightly less than T

. The resistance of a liquid to the formation of the crit-

ical cluster for nucleation is in fact much greater than its resistance to the growth of the

cluster.

4.2.1 The minimum cooling rate

Since the nucleation process occurs at the interface between the crystal and the surrounding

liquid, at a given instant only a very small part of the system is involved in the crystalliza-

tion process. For example, it is straightforward to see that within the volume of the liquid

a surface area of 1 cm

involves only 10

−7

or less volume. From the deﬁnition of the

steady-state nucleation rate J it follows that the number of crystalline nuclei δn appearing

4.2 Glass formation vs. crystallization 177

in a volume V of the liquid in time δt is given by JV δt. Hence the number of such nuclei

formed in time t

is obtained as

= V



Jdt, (4.2.1)

where we have ignored the temperature dependence of V . Thus the possibility of forming

a nucleus increases as we increase the volume V ,orJ , or the time t

. Let us assume that in

order to have n

= 1 we need to go up to time t

= t

∗

. This implies that, in order to bypass

the process of crystallization in this volume (so that not even a single nucleus is formed in

V ) and succeed in forming the glass, one must undercool the liquid to the glass-transition

temperature T

in time less than t

∗

. This sets a minimum cooling rate for bypassing the

crystallization process. The liquid must be cooled faster than this rate in order to suppress

the nucleation of the crystalline phase from the liquid. With a steady nucleation rate, the

time t

∗

is inversely proportional to the volume V in which the nucleation is taking place.

For a nucleation rate J in the steady state for the molar volume v

, the corresponding time

∗

≡ τ

is deﬁned to be the nucleation time,

J v

≡ τ

exp



G

∗



, (4.2.2)

where we have used (3.1.38) in writing the last equality and τ

= 1/(J

From eqn.

(4.2.1) it follows that in order to have n

< 1, so as to avoid crystallization, V and t

∗

should be correspondingly small. For example, Fig. 4.5 indicates that as T

increases

the corresponding nucleation rate falls, making t

∗

lower. Therefore, for a material with

higher T

≈ T

, a comparatively higher cooling rate is necessary in order to avoid

crystallization.

4.2.2 The kinetic spinodal and the Kauzmann paradox

As indicated above, a simple resolution of the Kauzmann paradox comes from assuming

the existence of a spinodal at a temperature T

> T

. The classical nucleation theory pre-

sented in the previous chapter does not consider the possibility of a spinodal (Trudu et al.,

2006; Wang et al., 2007). The spinodal refers to a situation in which a metastable phase

becomes locally unstable against ﬂuctuations. Whereas such conditions generally appear

in superheated liquids or overcompressed gases, for a supercooled liquid the situation is

not clear. From a computer-simulation study of freezing in a Lennard-Jones system (Trudu

et al., 2006) it appears that crystallization proceeds in a continuous and collective fashion

with increased supercooling. At deep supercooling the liquid is unstable and crystallization

is inevitable.

For volumes even lower than v

the volume dependence of the nucleation rate is rather ambiguous, since the corresponding

number of monomers involved is comparable to the critical size of the nucleus.

178 The supercooled liquid

Violation of the Stokes–Einstein relation

The possibility of the existence of a spinodal is controlled by two competing time scales,

namely the structural relaxation τ

of the undercooled liquid and the nucleation time τ

Generally, in order to make the supercooled liquid survive in the metastable equilibrium

state, the characteristic relaxation time τ

should be less than the corresponding nucle-

ation time τ

given in eqn. (4.2.2). This will ensure that ﬂuctuations in the metastable state

do not survive for long enough to start crystallization in the sample through nucleation.

At the freezing point T = T

the barrier to nucleation diverges (see eqn. (3.1.17)) and

hence the corresponding nucleation time τ

deﬁned in eqn. (4.2.2) becomes inﬁnite. The

relaxation time τ

, on the other hand, is ﬁnite at T

. Hence, near T

, τ

τ

and crys-

tallization is easily bypassed. As the liquid is further supercooled below T

, if there exists

a temperature T

< T

) at which the relaxation time τ

of the liquid exceeds the

corresponding nucleation time τ

, this will represent a limit of metastability. Below T

the supercooled liquid is unable to equilibrate and crystallization cannot be bypassed. Here

the crystalline state is the only equilibrium phase below T

. Such a temperature, if found

for a given liquid, represents a kinetic spinodal point. The barrier to nucleation is nonzero

at this temperature and the loss of stability is not of any thermodynamic origin. However,

it is not even clear a priori whether such a point exists for all liquids.

To test the above possibility, let us examine the prefactor τ

on the RHS of eqn. (4.2.2)

for τ

. As indicated in eqn. (3.1.56), τ

depends inversely on the average jump time τ

the monomers in the interfacial region. The movement of the monomer across the interface

is essential for the growth of the nucleus. The jump time τ

is inversely proportional to the

self-diffusion coefﬁcient, i.e., it is directly proportional to the viscosity η, assuming that the

Stokes–Einstein relation (Einstein, 1956) holds. In this case τ

(∼τ

) will tend to diverge

at T

introduced in the Vogel–Fulchure expression (4.1.5). However, it is clear from the

relation (4.2.2) that τ

will always be greater than τ

and hence the supercooled liquid

will seem to be able to stay along the metastable line without crystallization stepping in.

Hence there will be no spinodal at an intermediate T

. This possibility is shown by dashed

lines in Fig. 4.6. The crucial assumption involved in the above comparison of τ

and τ

is the validity of the Stokes–Einstein relation. If, however, there is a decoupling of the

translational diffusion from the structural relaxation, the Stokes–Einstein relation breaks

down and there is scope for an intermediate T

We can estimate the nucleation time in an independent manner. Let u

denote the growth

velocity of the crystallization nucleus front formed in an undercooled melt. It is expected

that u

will be inversely proportional to the jump time τ

of the monomers in the interfacial

region. As a simple approximation we assume the relation

(T

), (4.2.3)

where F

(T

) is a function of the relative undercooling T

from the freezing point. For

temperatures close to T

, F

should be directly proportional to T

, similarly to chemical

potential difference δμ given by (3.1.50). The number of nuclei per unit volume formed

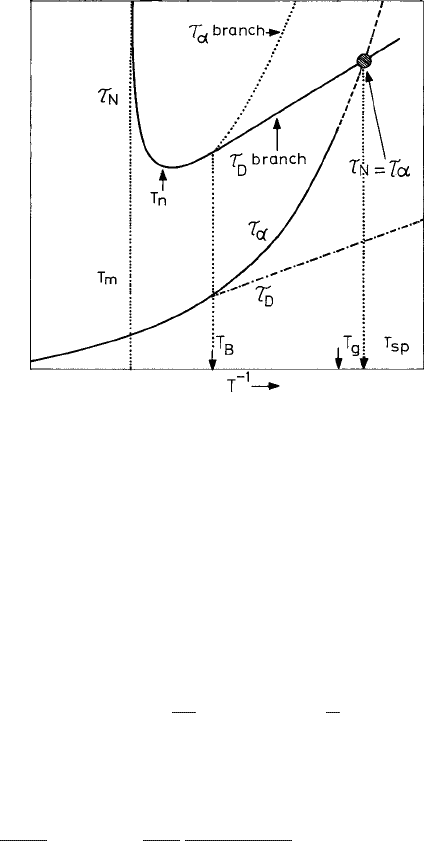
4.2 Glass formation vs. crystallization 179

Fig. 4.6 The role of violation of the Stokes–Einstein relation in resolving the Kauzmann paradox.

Temperature dependences of three characteristic times of a glass-forming liquid: (a) the structural

relaxation time τ

follows the Vogel–Fulcher law diverging at a low temperature T

; (b) the trans-

lational diffusion time τ

which decouples from τ

at T

; and (c) the nucleation time τ

,whichis

controlled by τ

below T

(see the text). τ

crosses τ

at T

, below which crystallization always

occurs before the liquid can relax to metastable equilibrium. Reproduced from Tanaka (2003).



American Physical Society.

between τ and τ + dτ is Jdτ . Therefore, after a time τ

each of these Jdτ nuclei has

grown for time τ

− τ at speed u

. Hence each of the nuclei in the unit volume grows to

radius u

(τ

− τ). The total volume fraction crystallized in time τ

is obtained as



dτ J

4π

(τ

− τ)

. (4.2.4)

Hence the time required for the crystallization of a small volume (fraction φ

of the liquid)

is obtained as



3φ

π Ju



1/4

= τ



3φ

πC

exp

[

βG

∗

]

(T )



1/4

≡ τ

(φ

, T ), (4.2.5)

wherewehaveusedtheresult(3.1.56) in Section 3.1.2 for the nucleation rate J . τ

has

contributions from τ

and f

(φ

, T ) with opposite trends. Near T

the function F

is large

while τ

is ﬁnite. On the other hand, at low temperatures below T

, F

is ﬁnite but the

time τ

grows sharply due to the fall of the self-diffusion in the deeply supercooled state.

Thus the nucleation time τ

has a minimum (nose) slightly below T

. With increased

supercooling τ

, however, grows much less rapidly than the structural relaxation time τ

This is because τ

is related to the inverse of the self-diffusion constant D

. The latter

now falls less rapidly than τ

since the Stokes–Einstein relation no longer holds.This

180 The supercooled liquid

is indicated in Fig. 4.6, showing that τ

eventually meets the τ

curve at a temperature

> T

, making crystallization dominant below this temperature. Thus the existence of

a kinetic spinodal above T

(and below T

) is feasible, leading to a possible resolution of

the Kauzmann paradox.

As an alternative to the above considerations, the existence of a kinetic spinodal has

been argued even in situations where the Stokes–Einstein relation continues to hold. This

involves taking into account the role of viscoelasticity of the melt in the formulation of the

classical nucleation theory.

Viscoelasticity of the melt

In the classical nucleation theory (CNT) described in the previous chapter, the conse-

quences of time-dependent stress relaxation (Turnbull, 1969) in the high-density melt due

to the formation of the nucleus are ignored. The initial response to an applied stress is

elastic over time scales short compared with that of structural relaxation. At high temper-

atures, close to the melting point T

, stress relaxation is fast while the nucleation time

is very large. At this stage the liquid quickly relaxes and viscoelastic effects are small.

However, at low temperatures τ

is large and the liquid develops solid-like behavior over

shorter time scales. Including the viscoelastic effect in the formulation of CNT at the sim-

plest level will involve taking into account the free-energy cost for the formation of the

nucleus the elastic contribution E

elastic

. An extension of the CNT has been proposed by

Cavagna et al. (2005). This involves modifying the expression (3.1.17) for the free-energy

difference G

to include an elastic contribution to the change in energy (G

−E

elastic

The elastic energy E

elastic

is approximated with a simple viscoelastic model in the form

elastic

= ε f (t), (4.2.6)

where ε denotes the scale of the elastic contribution to the free energy of the nucleus

and f (t) ≡ f (t/τ

) is a relaxation function satisfying the limiting values f (0) =1 and

f (∞) = 0. These limiting values of f (t) imply that for t  τ

, i.e., for time scales short

compared with the structural relaxation time τ

, the liquid exhibits solid-like behavior,

whereas for t  τ

the liquid is able to relax the stress, making the elastic contribution

to the free energy negligible. The barrier to the nucleation is now time-dependent and is

obtained as

G

∗

16πγ

3{|G

|−ε f (t/τ

)}

. (4.2.7)

The nucleation time deﬁned in (4.2.2) is now determined by imposing the self-consistent

relation

= τ

exp



16πγ

3{|G

|−ε f (τ

/τ

)}



(4.2.8)