Das Sh.P. Statistical Physics of Liquids at Freezing and Beyond

Подождите немного. Документ загружается.

3.2 A simple nonclassical model 131

3.2 A simple nonclassical model

We now discuss the process of formation of the critical nucleus in terms of a simple

schematic model (Bagdassarian and Oxtoby, 1994) in which the solid–liquid interface is

described in terms of a single order parameter. The present model is treated analytically and

also captures the important aspects of a more realistic density-functional approach to be

described in subsequent sections. The theory involves choosing simple approximate forms

for the free-energy proﬁle of the undercooled liquid having minima corresponding to the

stable and metastable bulk phases. The single order parameter ψ(r, t) used in the present

model is assumed to have ψ(r, t) = 0 for the metastable bulk liquid phase and some char-

acteristic constant value, say ψ

, for the stable bulk solid phase. The relative depth of the

deeper minima denotes the extent of supercooling of the system. The time evolution of this

order parameter is written in the standard time-dependent Ginzburg–Landau (TDGL) (Ma,

1976)form

∂ψ(r, t)

∂t

=−

δ[ψ]

δψ

, (3.2.1)

where [ψ] is the grand-canonical free energy expressed as a functional of the order

parameter ψ(r, t) and 

is the bare kinetic coefﬁcient. The term δ/δψ on the RHS of

(3.2.1) acts like a driving force (de Groot and Mazur, 1984) controlling the time variation

of the order parameter. Hence the equation

δ[ψ]

δψ

= 0 (3.2.2)

corresponds to a stationary nucleus. Now we write the grand potential functional of the

inhomogeneous solid liquid in the square-gradient approximation (Cahn and Hilliard, 1958)

of the order-parameter ﬂuctuation in terms of the simple expression

[ψ]=



ω[ψ]+|∇ψ(r, t)|

. (3.2.3)

Using this form of free energy in eqn. (3.2.1), the time evolution of ψ(r, t) becomes

− 

−1

∂ψ(r, t)

∂t

δω[ψ]

δψ

−∇

ψ(r, t). (3.2.4)

For the free-energy density ω(ψ) we choose the suggestive form

ω(ψ) = min

(ψ − ψ

)

+ 

(3.2.5)

which represents two intersecting parabolas as shown in Fig. 3.4, with their respective

minima at ψ = 0 and ψ = ψ

. The depths of the two minima differ by an amount 

which is a measure of the undercooling of the system. 

= 0 corresponds to the sit-

uation in which the two minima in ω are equal, signifying the coexistence of the liquid

and crystalline phases. The curvatures of the two parabolas corresponding to the liquid

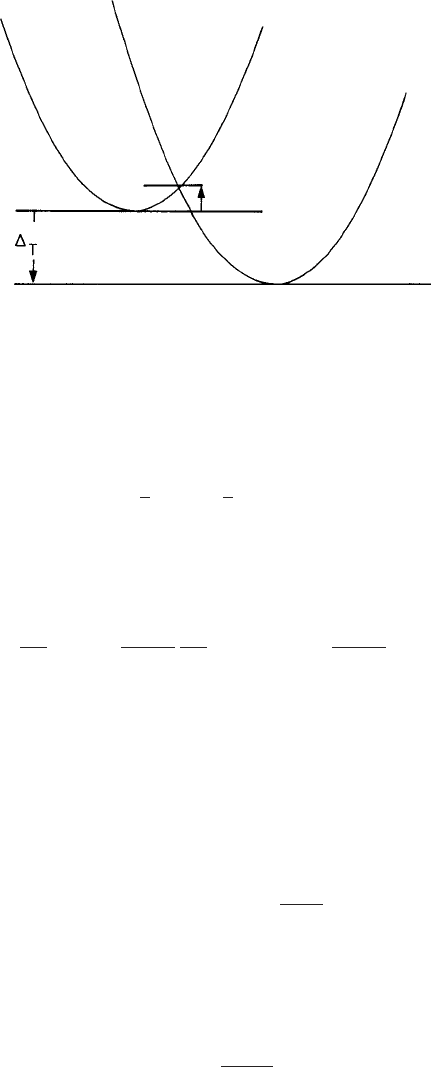
132 Crystal nucleation

Fig. 3.4 The schematic form of the potential energy taken as a combination of two parabolas as given

by eqn. (3.2.5). The height 

of the free-energy barrier between the two minima of the free energy

represents the extent of supercooling of the system.

and crystalline states are denoted by λ

and λ

, respectively. The parabolas intersect at the

order parameter value ψ = ψ

, which can be related to the undercooling 



−

(ψ

− ψ

)

. (3.2.6)

ψ(r, t) is the order parameter through the solid–liquid interface. The critical nucleus is rep-

resented by eqn. (3.2.2), which represents a saddle point for the free energy [ψ] (Bender

and Orszag, 1978). Note that

∂

∂t



δ[ψ]

δψ

∂ψ

∂t

=−





δ[ψ]

δψ



, (3.2.7)

so that  always decreases while the optimum order-parameter proﬁle is being determined

by the condition (3.2.2). In solving this equation for ψ, we note that for the part ψ>ψ

we need to use the solid part of the free-energy proﬁle (the parabola with its minimum at

), whereas for ψ<ψ

the liquid part (the parabola with its minimum at 0) is to be used.

In the above choice of the free energy in the double-parabola form there is automatically

the limit in which the liquid loses its metastability with respect to the solid, i.e., ψ

= 0.

This limiting situation is characterized by the undercooling 

obtained from (3.2.6) as



≡ 

=−

(3.2.8)

and represents a spinodal in the present model.

The basic equation describing the critical nucleus therefore follows from (3.2.4) in the

form of a second-order differential equation for the order-parameter ﬁeld in the steady

state,

∇

ψ =

δω[ψ]

δψ

. (3.2.9)

3.2 A simple nonclassical model 133

For representing the spherical nucleus we consider a spherically symmetric order-parameter

proﬁle. Using the corresponding spherically symmetric form of the ∇

operator, we obtain

the following differential equations for the order parameter from eqn. (3.2.2):

ψ(r)

dψ(r)

−[ψ(r) − ψ

]=0, for ψ<ψ

, (3.2.10)

ψ(r)

dψ(r)

−¯ν

ψ(r) = 0, for ψ>ψ

. (3.2.11)

In writing the above two differential equations we express length r in units of 1

√

(i.e.,

√

r → r) and deﬁne the parameter ¯ν =

√

/λ

. The two differential equations stated

above are obtained by using in the equation (3.2.2) the respective parabolic form for the

grand potential function  as stated in eqn. (3.2.5). The parameter ¯ν denotes the relative

curvatures of these two parabolas representing the order-parameter dependence of the free

energy . The crossover value of the order parameter ψ = ψ

marks the proximity to

the stable liquid or the crystalline minimum. The crystalline nucleus is identiﬁed with the

order-parameter value ψ>ψ

, since in this case the system is closer to the free-energy

minimum at ψ = ψ

. The order-parameter values ψ<ψ

, on the other hand, correspond

to the liquid state, which is characterized by the minimum at ψ = 0.

3.2.1 The critical nucleus

Equations (3.2.10) and (3.2.11) are solved to obtain the following relation among ψ

, ψ

and r

for the critical nucleus:

= ψ

1 −r

−1

tanh r

1 +¯ν tanh r

. (3.2.12)

The solution of eqns. (3.2.10) and (3.2.11) under appropriate boundary conditions to reach

the above result (3.2.12) is given in Appendix A3.1. The boundary r = r

therefore is a

marker for the crystalline phase in this case and is a natural identiﬁcation of the radius

of the critical nucleus corresponding to the condition (3.2.2).Asweseeineqn. (A3.1.4)

of Appendix A3.1.1, ψ

(0) →ψ

, i.e., the order parameter at the center of the nucleus

approaches the bulk-solid value. The relation (3.2.12) between ψ

and ψ

is useful in deter-

mining how the critical radius changes with the undercooling 

. Two limiting cases are

of interest here.

Near coexistence

In this limit the undercooling 

→0 and it then follows from (3.2.6) that ψ

→ψ

(1+¯ν). Identiﬁcation of the same relation from (3.2.12) requires tanh r

→ 1 and r

−1

→0.

This corresponds to r

→∞. In order to ﬁnd the leading-order relation between r

and 

we simplify the relation (3.2.6) to leading order in 

− ψ

=¯νψ



1 −





. (3.2.13)

134 Crystal nucleation

Upon inverting the above relation expressing ψ

in terms of ψ

with the approximation

≈ (1 +¯ν)ψ

, we obtain

1 +¯ν



¯νλ

+ O

(



)

. (3.2.14)

For large r

, to leading order (3.2.12) reduces to

= ψ



1 +¯ν

−

−1

1 +¯ν



. (3.2.15)

On comparing (3.2.14) and (3.2.15) we obtain the relation



=−



¯ν

1 +¯ν



. (3.2.16)

In the above limit of coexistence 

→ 0(r

→∞)wehave





¯ν

1 +¯ν



, (3.2.17)

where



=

/

is the undercooling of the system relative to that at the spinodal point.

The spinodal limit

This is characterized by the situation ψ

→0, with the corresponding undercooling 

being given by (3.2.8). In this case it follows from (3.2.12) that tanh r

→r

, i.e., r

→0,

implying that the liquid state is always unstable. In the limit r

→0 the relation (3.2.12)

reduces to the form ψ

≈ ψ

/3. On using this in the deﬁnition (3.2.8) for the undercool-

ing 

we obtain



=−



1 −

2ψ



=−



1 −



. (3.2.18)

The radius of the critical nucleus r

approaches zero with the supercooling 

correspond-

ing to the spinodal point as,

∼



1 −



1/2

. (3.2.19)

3.2.2 The free-energy barrier

The free energy for the formation of the critical nucleus relative to the liquid is computed

in the present schematic model as



= 4π



∞

dr r



ω[ψ(r, t)]+

|∇ψ(r, t)|



, (3.2.20)

where the subscript NC refers to a nonclassical quantity to distinguish it from the corre-

sponding quantity in classical nucleation theory. In Appendix A3.1.1 we demonstrate that

3.2 A simple nonclassical model 135

evaluating the RHS of eqn. (3.2.20) corresponding to the critical nucleus proﬁle

leads to



4πr



− 4πr





1 −r

−1

tanh r

1 +¯ν tanh r



(

¯ν +r

−1

)

. (3.2.21)

The last equality above is reached by using the relation (3.2.12) for ψ

/ψ

.Usingthe

leading-order expansion of tanh r

≈ 1 − 2exp(−2r

) for large r

the second term on the

RHS can be further simpliﬁed to obtain



4πr



− 4πr



¯ν

1 +¯ν

−1





. (3.2.22)

Upon identifying the RHS of (3.2.22) with the surface term in the classical expression

(3.1.9) for the free energy of the critical nucleus, we obtain the following expression for

the surface free energy:

=−



¯ν

1 +¯ν



≡



¯ν

1 +¯ν



. (3.2.23)

The free energy 

and radius r

of the optimum cluster in the present schematic

model can be compared with the corresponding results of the CNT. To make such a com-

parison we need to identify the relevant quantities in the present model with their corre-

sponding counterparts in the CNT. This is done primarily on the basis of the similarities

between the expression (3.2.22) for the free energy in the schematic model and the classical

expression for the same quantity as given by (3.1.17). Thus r

is taken as the radius of the

critical nucleus and 

as the free-energy difference G

in the CNT. The surface tension

is chosen from (3.2.23). Using the expression for the (3.1.17) for G

∗

we obtain the

free energy (in units of 

)as



∗

16π





¯ν

1 +¯ν



. (3.2.24)

The radius of the critical nucleus in the CNT is obtained from (3.1.18) as

∗

=−

2γ





¯ν

1 +¯ν



, (3.2.25)

which agrees with the corresponding result (3.2.17) in the schematic model close to coex-

istence. For a chosen free-energy landscape (characterized by ¯ν) and a given undercooling

(determined by



), the CNT expressions for the free energy and the radius of the critical

nucleus are given by (3.2.24) and (3.2.25), respectively.

In the nonclassical schematic model, on the other hand, estimates of the free energy and

radius of the critical nucleus are obtained by directly solving eqns. (3.2.12) and (3.2.6).

These two equations can be conveniently written as

136 Crystal nucleation

ϒ ≡

1 −r

−1

tanh r

1 +¯ν tanh r

, (3.2.26)

where ϒ is obtained from the solution of the equation

(

1 −¯ν

)

− 2ϒ +

(

1 −



)

= 0. (3.2.27)

For a given value of ¯ν the critical radius r

is obtained as a function of the relative under-

cooling



. The free-energy barrier 

∗

(expressed in units of 

) to formation of the

critical nucleus is obtained from (3.2.21) as



∗

4πr



− 4πr

(

¯ν +r

−1

)

. (3.2.28)

Therefore the critical radius r

(¯ν,



) and 

∗

(¯ν,



) are determined simultaneously.

The radius r

of the critical nucleus in the present model can be either higher or lower than

its counterpart R

∗

in the CNT depending on the value of the parameter ¯ν and the extent

of undercooling



. Results for the radius of the critical nucleus from these two theories

agree in the limit of zero supercooling, i.e., at coexistence, at which r

→∞.Thesame

behavior is observed with respect to the height of the free-energy barrier to critical-nucleus

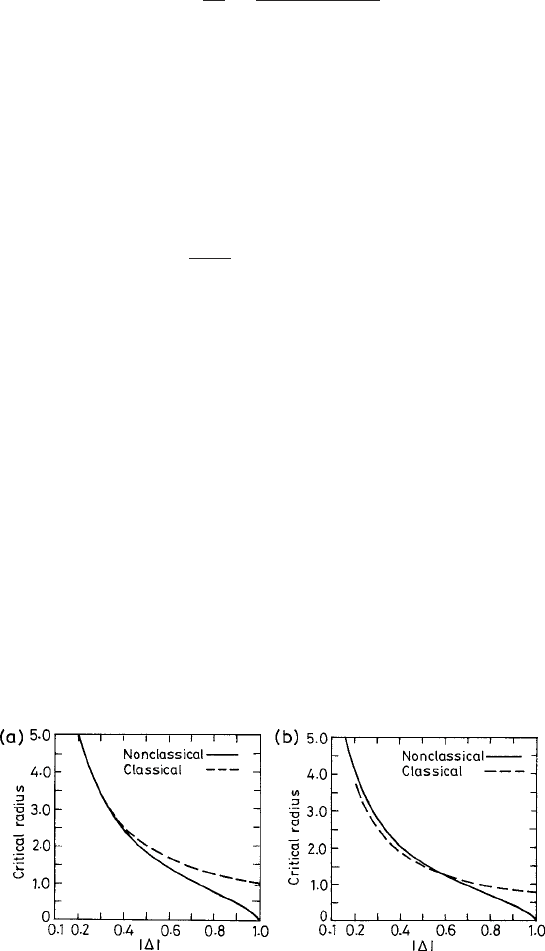
formation computed in the above two theories. The dependence of the critical radius r

on the degree of undercooling



is shown in Fig. 3.5. We choose for the parameter

¯ν = 0.5 here. In Fig. 3.5, we see that the predictions of the nonclassical theory can be

higher and lower than the corresponding CNT predictions, depending on the undercool-

ing. Both trends are also predicted within the different types of DFT models discussed in

the next section. We have focused here primarily on the formation of the critical nucleus.

The dynamics of its evolution is also obtained (Bagdassarian and Oxtoby, 1994) by solv-

ing the corresponding TDGL equations (3.2.1) for speciﬁc choices of the free-energy

landscape deﬁned in terms of ¯ν.

Fig. 3.5 The critical radius r

in units of λ

−1/2

(see the text) vs. the undercooling



(see the text)

for two values of the parameter ¯ν (see text): (a) 1.0 and (b) 0.6. The corresponding values of the

critical radius obtained from the CNT in the respective cases are also shown for comparison. From

Bagdassarian and Oxtoby (1994).

 American Institute of Physics.

3.3 The density-functional approach 137

3.3 The density-functional approach

The density-functional theory outlined in the previous chapter has been used for under-

standing the nucleation phenomena starting from basic principles of statistical mechanics.

Compared with the model described in the previous section, here a more realistic descrip-

tion of the crystal and the liquid state is chosen. In this formulation the interaction potential

between the constituent particles in the system is the primary input. As we have seen

in Chapter 2 regarding studying the bulk crystalline phase or the interfaces, the grand-

canonical potential is minimized with respect to the inhomogeneous density function in

order to identify the critical nucleus. In the DFT formulation, unlike in the CNT described

above, the effect of curvature of the interface in the computation of the free energy of the

clusters is taken into account. The difference  between the grand-canonical potentials

of the inhomogeneous state (consisting of the nucleating bubble) and of the homogeneous

liquid state is optimized with respect to the inhomogeneous density function. This auto-

matically identiﬁes the critical nucleus, i.e., corresponding to the optimum density function

(x) representing the crystal nucleus in the melt, we have

[n

(x)]=

+ G

∗

, (3.3.1)

where G

∗

denotes the free energy required for the formation of the critical nucleus (see

eqn. (3.1.15) in the discussion of the CNT above). In formulating the appropriate DFT

for the present case it is important to notice that the critical nucleus is in fact dynami-

cally unstable. However, this instability is with respect to the variation of the number of

monomers in the critical nucleus, which can either grow or shrink as a result of ﬂuctuations

in the number of monomers. This is therefore relevant when the grand-canonical ensemble

is used to describe the critical nucleus (with a ﬁxed number of particles, on the other hand,

the critical nucleus is the state of minimum free energy and hence corresponds to a ther-

modynamically stable state). The critical nucleus represents a saddle point in the function

space of density, having one unstable direction with respect to the particle number. Hence

the optimum density distribution of the critical nucleus is determined from the solution of

the Euler–Lagrange equation



δ

δn(r)



n(r)=n

(r)

= 0. (3.3.2)

The identiﬁcation of the critical nucleus and its size as depicted through the optimum den-

sity proﬁle follows in a natural way from the optimization of the thermodynamic function

in the DFT approach to this problem. However, it is still a mean-ﬁeld approach and the

treatment of the smallest clusters containing a few molecules can only be approximate.

3.3.1 The square-gradient approximation

A crucial ingredient of the DFT is the choice of the test density function with respect

to which the appropriate thermodynamic functional is minimized. We have discussed in

138 Crystal nucleation

the previous chapter (see, for example, eqn. (2.4.32)) how the density-functional model is

extended to study the plane interface of the liquid and the crystal. The parametrization of

the density function for the critical nucleus is done in a manner similar to that done in the

DFT studies for the plane interface of the liquid and crystal. The spatial dependences of the

parameters in the inhomogeneous density function characterizing the nucleus are chosen

in such a manner that, away from the surface of the nucleus, near the center, the structure is

crystalline, while at large radial distances the uniform liquid state of the melt is obtained.

A typical example follows from the ansatz (2.1.42) for the density function generalized in

the following manner for the spherical nucleus (Harrowell and Oxtoby, 1984):

(r) = n



1 + η(r ) +



(r)e

· r



, (3.3.3)

in terms of a set of local order parameters, γ(r) ≡{η(r), A

(r)}. The corresponding

boundary conditions are η(r →∞) = 0 for the liquid state and η(r → 0) = (n

−n

)/n

which is the fractional change of density on solidiﬁcation, n

being the average density

of the solid state. In the discussion below we generalize this approach. We assume that

the inhomogeneous density function n

(r;γ) is parametrized in terms of locally vary-

ing amplitudes denoted by γ ≡{γ

(r)} for i = 1,...,m.Theγ

form a set of local

order parameters. The grand potential function  for the inhomogeneous state is computed

within the square-gradient approximation. The latter is applied to evaluate the nonlocal

contributions to the thermodynamic potential involving the densities at two different spa-

tial points. To illustrate this approximation, we consider the local and nonlocal parts of

[n(r)],

[n]=F

+ F

− μ



n(r)dr. (3.3.4)

The subscripts of the ﬁrst and second terms on the RHS denote the ideal and the excess

parts of the Helmholtz free energy, respectively. The ideal part F

is represented in terms

of a local functional of the density and the interaction or the excess part F

involves

nonlocal contributions. For the uniform state with constant order parameters these are given

in Chapter 2 in eqns. (2.1.27) and (2.1.38), respectively. The grand potential  of the

inhomogeneous state corresponding to the density function n

(x, {γ

}) is obtained in terms

of a functional Taylor-series expansion around the uniform liquid state.

β=



;γ)ln



;γ)



−



;γ)− n

)



c(x

, x

)δn

;γ(x

))δn

;γ(x

)) +···, (3.3.5)

where the direct correlation function c(r) (Ohnesorge et al., 1991) is deﬁned as

c(x

, x

) =−β



]

δn

;γ)δn

;γ)



. (3.3.6)

The above expression is similar to the expansion around the uniform liquid state shown

in eqn. (2.1.41) in Chapter 2. Note that the RHS of (3.3.5) involves the inhomogeneous

3.3 The density-functional approach 139

densities and hence the corresponding order parameters γ

at two different spatial points

and x

in the interaction part. This part is simpliﬁed by adding to the local contribu-

tion corrections evaluated within the square-gradient approximation. On expanding the

amplitudes {γ } up to second order in spatial derivatives, we obtain for the ith member of

the set

) = γ

) +{x

· ∇}γ

) +

· ∇}

), (3.3.7)

where x

−x

= x

and ∇ indicates the derivatives with respect to the spatial variation of

the local order parameters. The density δn

;γ(x

)) is now expressed within the above

square-gradient approximation as

;γ(x

)) = n

;γ(x

)) +



∂n

)

∂γ



· ∇}γ

· ∇}





∂

)

∂γ

· ∇}

, (3.3.8)

where ∂n

)/∂γ

denotes the partial derivative of the density n

;γ(x

)) with respect

to its dependence on the order parameter γ

. We will assume here a linear dependence

of the ﬁeld γ

on the density function (similar to the relation (2.4.32) stated above for the

interface problem) and hence ignore contributions from the last term on the RHS of (3.3.8).

Substituting (3.3.8) for the density ﬂuctuation δn

;γ(x

)) reduces (3.3.5) to the form

β=



;γ)ln



;γ)



−



;γ)− n

)



c(x

, x

)δn

;γ(x

))δn

;γ(x

))





∂n

)

∂γ

c(x

, x

)δn

;γ(x

)){x

· ∇}

. (3.3.9)

In obtaining the above result we have set the contribution from the linear term in the

expansion (3.3.7) to zero using the fact that the spatial Fourier transform c(k) of the direct

correlation function c(r) at the RLV is c



) = 0 since the K

correspond to peaks of the

structure factor. Let us consider the different terms on the RHS of (3.3.9).

(a) The ﬁrst three terms on the RHS of (3.3.9) constitute to leading orders a contribution

that is expressed in terms of a grand potential density D(x) as

β

[γ ]=



;γ(x

)) ln



;γ(x

))



− δn

;γ(x

))



c(x

, x

)δn

;γ(x

))δn

;γ(x

))

≡



dx D[γ

(x)]. (3.3.10)

140 Crystal nucleation

D involves the order parameter γ

(x) only locally. This part of the grand potential is

denoted as 

with the subscript u signifying the fact that the functional dependence

of 

is the same as that for the uniform system with constant order parameters. In

(3.3.9) 

is being evaluated with the Ramakrishnan–Yussouff functional Taylor-series

expansion. Alternatively, this local contribution can be computed using the MWDA in

the same manner as formulated for the bulk phases, for a more accurate evaluation of

the grand potential.

(b) The last term on the RHS of (3.3.9) is further simpliﬁed with a partial integration and

using the substitution

∇

;γ(x

)) =



∂n

)

∂γ

∇

), (3.3.11)

where ∇

denotes the spatial derivative with respect to the corresponding spatial com-

ponent x

. The coefﬁcient of the square-gradient term, i.e., of ∇

∇

, is expressed

as a kernel #

αβ

. The latter is evaluated to leading order in terms of the integral per-

formed with V

−1

and is expressed in terms of the local order parameters γ(x),

αβ

[γ(x)]=−



∂n

)

∂γ

∂n

)

∂γ

c(x

, x

;γ(x))dx

. (3.3.12)

On combining the above terms we therefore obtain the following result for the differ-

ence between the grand potential of the inhomogeneous state and that of the uniform

liquid:





⎧

⎨

⎩

D[γ

(x)]+

αβ



i, j

αβ

[γ(x)]∇

(x)∇

(x)

⎫

⎬

⎭

. (3.3.13)

Thus, in summary, the ﬁrst term on the RHS of (3.3.13) represents the thermody-

namic potential  obtained as a local functional of the order parameter γ(x) while the

second term represents the contribution (evaluated within the square-gradient approxi-

mation) due to the variation of the local amplitudes γ

through the interface region. The

critical nucleus is identiﬁed by optimizing the thermodynamic grand-canonical poten-

tial , i.e., solving the corresponding Euler–Lagrange equation (3.3.2). In the present

context these equations simplify to ordinary differential equations,



δ

δγ

(r)



= 0. (3.3.14)