Das Sh.P. Statistical Physics of Liquids at Freezing and Beyond

Подождите немного. Документ загружается.

5.3 Linear ﬂuctuating hydrodynamics 241

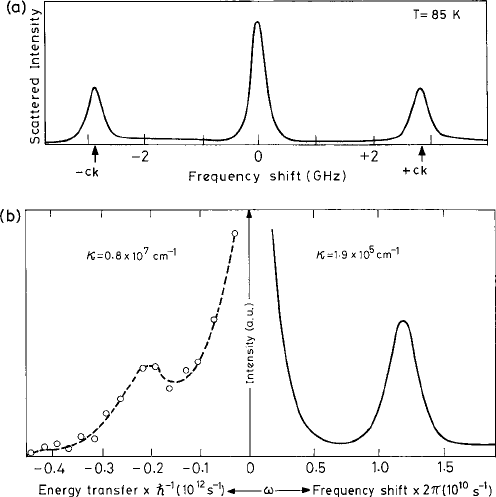
Fig. 5.2 (a) A schematic diagram showing the Fourier transform S(k,ω) of the density–density

correlation function in a liquid. The two symmetrically placed “Brillouin peaks” at ω =±cq are

of Lorentzian form with half-width ∝k

and are caused by propagating sound waves in the isotropic

liquid. The central “Rayleigh peak” is of width ∝ k

and represents heat diffusion. Note that this heat

mode has been ignored in the formulation of expression (5.3.87). Reproduced from Fleury and Boon

(1969, 1973). (b) Brillouin peaks in liquid neon. Left panel: neutron-scattering data for T = 70 K,

ρ = 0.48 g cm

−3

shown by open circles. The dashed line is a ﬁt with a hydrodynamic model similar

to what is described in the text but including the heat mode. Right panel: light scattering data at

T = 25 K and normal liquid density from Fleury and Boon (1969). The intensities of the scattering

are shown in arbitrary units. The κ denotes corresponding wave-vector values in inverse Ångström

units (Å

−1

).FromBell et al. (1975). Both parts

 American Physical Society.

The correspondence to experimental results is displayed in Fig. 5.2(b). The two Lorentzian

peaks at ω =±cq with half-width 

correspond to the sound poles and are termed Bril-

louin peaks. The shear diffusion mode appears as a central diffusive peak of width ν

Note that we have considered only four of the hydrodynamic modes, out of the total of ﬁve

modes present in the isotropic ﬂuid, and ignored the energy conservation for simplicity.

The latter gives rise to a diffusive heat mode (Forster, 1975) in the liquid and would have

added a central diffusive peak, termed the Raleigh peak (as shown in Fig. 5.2(a)), of width

proportional to the thermal conductivity of the liquid. The result for the maximum fre-

quency ω

(k) of the longitudinal-current correlation function seen in MD simulations for

various wave numbers k is shown in Fig. 5.3. The ﬂuctuating-hydrodynamics description is

242 Dynamics of collective modes

Fig. 5.3 A plot of the maximum frequency ω

(k) of the longitudinal-current correlation function

seen in MD simulations by Rahman (1968) of hard spheres vs. the wave vector in inverse Ångström

units (Å

−1

). The solid line is a ﬁt with an empirical model with adjustable ﬁtting parameters.

Reproduced from Akcasu and Daniels (1970).

 American Physical Society.

easily generalized to more complex systems, such as multi-component ﬂuids (Cohen et al.,

1971; March and Tosi, 1976) and molecular liquids (Gray and Gubbins, 1984).

The generalized hydrodynamics

In the discussion of hydrodynamic modes above we have ignored in the theoretical treat-

ment for simpliﬁcation any wave-vector dependence of the bare-transport-coefﬁcient matrix

as well as the structure factor χ of the liquid. In reality, however, the structure factor

has a strong wave-vector dependence with a sharp peak at the wave number corresponding

to the hard core of the particle interactions (see Chapter 1). The bare transport coefﬁ-

cients are also dependent on the corresponding length scales over which transport is being

considered. The concept of hydrodynamic modes can be extended to short distances by

considering the hydrodynamic equations at wave vectors that are large – comparable to

that of the ﬁrst peak in the static structure factor. Although the assumption of slow vari-

ations used in obtaining the hydrodynamic equations is not valid at short length and time

scales, it is plausibly assumed that the deviations occur in a subtle and gradual manner.

Thus, while retaining the basic structure of the equations, the hydrodynamic description

can be extended by replacing the relevant thermodynamic properties or transport coefﬁ-

cients by functions that can vary in space or in both space and time (Chung and Yip, 1969;

Akcasu and Daniels, 1970; Ailawadi et al., 1971). The resulting theory, which describes

the dynamic behavior of the ﬂuid over a wider range of spatial and temporal variations,

is termed generalized hydrodynamics (Kadanoff and Martin, 1963; Boon and Yip, 1991).

In applying this continuum hydrodynamic description to liquids, it is useful to note that

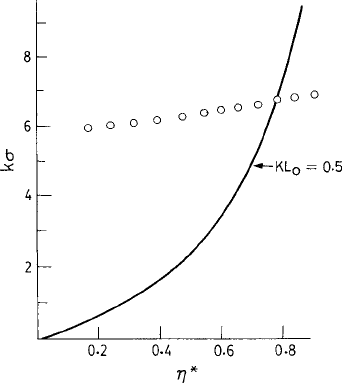
5.3 Linear ﬂuctuating hydrodynamics 243

Fig. 5.4 A plot of kσ vs. the density nσ

for the hard-sphere system corresponding to kl

= 0.5,

where l

is the corresponding mean free path. Hydrodynamics applies below this line. The positions

of the structure-factor peaks are also shown with open circles. Reproduced from Lutsko et al. (1989).

 American Physical Society.

the length scale of the ﬂuctuations does become comparable to the coarse-graining length

involved in such a picture. However, with increasing density of the liquid the mean free

path becomes smaller than the particle size and the validity of the continuum hydrody-

namic treatment improves. In Fig. 5.4 we display for a hard-sphere system a comparison at

various liquid densities between the structure-factor peak k

and the k at which hydro-

dynamics is valid (i.e., kl

< 1, where l

is the mean free path at the corresponding

density). For a dense liquid the two wave numbers are comparable. We discuss below

the generalization of the hydrodynamics along these lines speciﬁcally for the case of a

hard-sphere ﬂuid.

The nature of the dynamics of the ﬂuctuations of the conserved densities at short wave-

lengths is obtained by making an extension of the conventional hydrodynamics to short

length scales. A hard-sphere system provides the simplest example. We consider here the

complete set of variables consisting of {ρ,g, T }, respectively denoting the density, momen-

tum, and kinetic energy. There is no potential energy in this case of hard spheres. From the

matrix eqn. (5.3.23) correlation functions are computed in the crucial short-time approxi-

mation. In this limit the contribution from the dynamic part K

(d)

of the memory function

K is set equal to zero. For the hard-sphere system with instantaneous collisions this is

still a reasonable approximation for studying the dynamics up to even long times. The

treatment is considered at the level of uncorrelated binary collisions, which is a reason-

able approximation at densities close to freezing. The static part of the memory function

(d)

is computed from (5.3.31) involving the Liouville operator L. For the special case

244 Dynamics of collective modes

of discontinuous hard-sphere potentials, the time dependence of the dynamic variable

A(t) = e

A is generated by operators L

and L

−

for t > 0 and t < 0, respectively.

respectively involve the corresponding hard-sphere collision operators T

(Résibois

and de Leener, 1977). The operators L

are identical for ﬂuids with continuous interaction

potentials. The matrix elements K

(s)

are computed using the explicit forms of the collision

operator. The equal-time correlation-function matrix S

in this case is diagonal with the

nonzero elements

ρρ

= m

nS(x), (5.3.94)

2β

, (5.3.95)

= S

, (5.3.96)

where we denote the wave number q by a dimensionless variable x =qσ involving the

hard-sphere diameter σ . S(x) is the static structure factor for the hard-sphere liquid.

A straightforward calculation gives for the static part, K

(s)

⎡

⎣

0 x 0

(x) i

(x) xξ(x)

0 −xξ(x) iD

(x)

⎤

⎦

, (5.3.97)

where c

= 1/(βmS(x )) is now the wave-vector-dependent speed of sound. The various

wave-vector-dependent functions are given by

ξ(x) = 1 + 3y

(x)

, (5.3.98)

(x) = ν

[1 − j

(x)], (5.3.99)



(x) = ν

[1 − j

(x) + 2 j

(x)], (5.3.100)

with j

denoting the spherical Bessel function of order l. D

(x) and 

(x) are, respectively,

the generalized heat-diffusion constant and sound attenuation. ν

represents a microscopic

frequency ν

= 2/(3t

), t

being the Enskog time between collisions (Résibois and de

Leener, 1977) of the hard spheres,

√

, (5.3.101)

where v

= 1/(βm) is the thermal velocity of the ﬂuid particles and Y = 4πϕg(σ )

expressed in terms of the hard-sphere packing fraction ϕ = πnσ

/6. This is the same as the

time deﬁned in eqn. (1.3.41). The density–density correlation function F(q, t) (normalized

with respect to its equal-time value) at large q is obtained in terms of the three exponentially

relaxing modes, i.e.,

F(q, t) =



μ=1

(x)e

−z

(x )t

, (5.3.102)

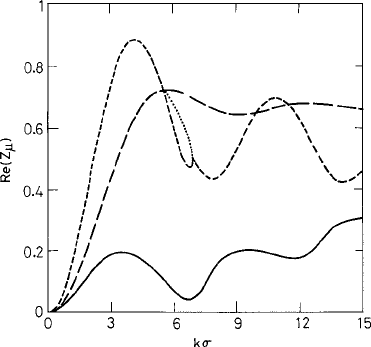
5.3 Linear ﬂuctuating hydrodynamics 245

Fig. 5.5 The real part of the eigenvalues −z

(k) (μ = 1,...,5) vs. k for the hard-sphere ﬂuid at

packing fraction ϕ = πnσ

/6 = 0.471. The curves correspond to the pair of complex-conjugate

sound modes (dotted), the heat mode (solid), and two degenerate shear modes (dashed). Reproduced

from Das and Dufty (1992).

 American Physical Society.

where z

(x) are the three eigenvalues of the matrix (5.3.97). These z

(μ =1, 2) in the

small-q limit reduce to the propagating modes described above in eqn. (5.3.89).Thewave-

number-dependent functions D

(x), 

(x), and η

(x) play the role of generalized trans-

port coefﬁcients representing dissipative effects over short length scales. These generalized

transport coefﬁcients in the small-wave-number limit reduce to the corresponding results

obtained from the Enskog theory (Résibois and de Leener, 1977) for a hard-sphere system

in which only the collision contribution has been kept (Kirkpatrick, 1985b). Similarly, the

eigenvalues for the shear modes are z =−η

(q), where

(q) = ν

1 − j

(x) − j

(x)

(5.3.103)

is the generalized shear viscosity. Figure 5.5 shows the real part of the eigenvalues −z

(q)

(μ = 1,...,5) extended to large q, for the hard-sphere system at packing fraction ϕ =

0.471. The Percus–Yevick solution (Ashcroft and Lekner, 1966) with Verlet–Weiss correc-

tion (Verlet and Weiss, 1972; Henderson and Grundke, 1975) for the structure factor S(q)

has been used in computing the matrix elements of (5.3.97). The propagating pair of sound

modes (shown by the dotted line) crosses over to a pair of real modes for an intermediate

wave-number range. The most interesting feature is the behavior of the heat mode (solid

line), which close to the freezing point becomes soft near the peak of the structure factor

of the liquid. This is a consequence of S

−1

(q) being small there. Analysis of the ampli-

tude factors of the eigenmodes of the matrix K

(s)

at this wave number indicates that the

soft mode essentially represents density ﬂuctuations. At high density the softening is pro-

nounced and it corresponds to very slow dynamics near the diffraction peak (de Gennes,

1959) and is generally termed de Gennes narrowing in liquid-state physics. The two shear

246 Dynamics of collective modes

modes (dashed lines) are identical in the isotropic liquid. From the continuity equation

it follows directly that the longitudinal-current correlation function is simply related to

the density correlation function. The result for the maximum frequency ω

(k) of the

longitudinal-current correlation function seen in MD simulations for various wave num-

bers k is shown in Fig. 5.3. For small wave numbers simple propagating sound waves are

obtained and near the structure-factor peak there is strong slowing down as predicted from

the theory. The nature of the ﬂuctuations of the conserved densities at short length scales as

obtained from the generalized hydrodynamic approach described above closely resembles

that of a microscopic kinetic-theory approach (de Schepper and Cohen; 1980, 1982).

5.4 Hydrodynamics of a solid

The ﬂuctuating-hydrodynamics description of the crystal is obtained with the equations of

motion for an extended set of slow modes consisting of the usual hydrodynamic modes due

to the microscopic conservation laws (similar to those for an isotropic liquid) as well as

the new modes which occur due to long-range order in the system. The latter are referred

to as the Nambu–Goldstone modes. In the context of the freezing of a liquid into a crys-

tal these are the transverse sound modes characteristic of the solid state and occur as a

consequence of the breaking of the isotropic symmetry of the liquid state. Breaking of a

microscopic symmetry and having long-range order makes the static correlation soft (i.e.,

diverging as q

−2

) and gives rise to the slow modes as described by the Goldstone theorem.

We discuss this theorem below, starting from general considerations. This also provides a

suitable recipe for deﬁning the additional slow modes which occur due to symmetry break-

ing. We apply it to the case of the crystal in order to deﬁne the Goldstone modes for the

crystal.

The Goldstone theorem

The Goldstone theorem in relativistic quantum ﬁeld theory refers to the existence of a

massless boson particle corresponding to the breaking of a continuous symmetry of the

Lagrangian. We discuss this theorem here in the context of breaking of the continuous

symmetry of a many-particle system. The operator

Q which generates the continuous sym-

metry is conserved, i.e., it commutes with the Hamiltonian operator

H. In the classical

description this will imply that the Poisson bracket of the conserved quantity Q with the

Hamiltonian H vanishes,

{Q, H}=0. (5.4.1)

The density a(x) corresponding to A is deﬁned as

Q =



dx a(x), (5.4.2)

and satisﬁes the continuity equation

∂a

∂t

+∇· j

= 0, (5.4.3)

5.4 Hydrodynamics of a solid 247

with the corresponding current being j

. In the Fourier-transformed form eqn. (5.4.3) takes

the form

˙a(q, t) + qj

(q, t) = 0, (5.4.4)

where j

is the longitudinal component of the current j

(q) in the direction of q.Now,let

us assume that there exist two ﬁelds ψ(x) and ˜ϕ(x) such that the Poisson bracket of the

former with Q is proportional to the latter,

{˜ϕ(x), Q}=ξ

ψ(x), (5.4.5)

where ξ

is a constant. The equilibrium average of ψ(x) is given by

ψ(x)=



dψ(x)

(), (5.4.6)

where 

() is the equilibrium probability distribution for the phase-space element d.It

is straightforward to prove that



dψ(x)

() = ξ

−1



d{˜ϕ(x), Q}

()

= ξ

−1



d ˜ϕ(x){

(), Q}, (5.4.7)

wherewehaveusedeqn. (5.4.5) in writing the ﬁrst equality. For the second equality we

have used the general properties of the phase-space average, similarly to what was done in

the mathematical manipulations involved in reaching eqns. (5.3.34)–(5.3.39) in Section

5.3.1. If the continuous symmetry generated by Q is maintained thermodynamically, then

from eqn. (5.4.1) it follows that

{

(), Q}=0 (5.4.8)

and hence, using the relation (5.4.7), we obtain that

ψ(x)=0. (5.4.9)

On the other hand, when the continuous symmetry generated by Q is broken, the Poisson

bracket on the LHS of eqn. (5.4.8) is nonzero and hence

ψ(x)=ψ

= 0. (5.4.10)

Therefore, with the triad of ﬁelds {˜ϕ, ψ, a} satisfying eqn. (5.4.5), we can identify an order

parameter ψ(x) to describe the broken symmetric state with long-range order. With the

breaking of the continuous symmetry generated by Q the system passes into a phase that

is characterized by the order parameter ψ

We now prove the important result that in the broken-symmetric state the Fourier trans-

form of the static susceptibility corresponds to ˜ϕ(x).Letϕ

be the spatial Fourier transform

of ˜ϕ(x), so that

(q) ≡|ϕ

 (5.4.11)

248 Dynamics of collective modes

diverges as q

−2

for small q. In real space this signiﬁes long-range order in ˜ϕ(x) correlation,

i.e., the equilibrium averaged time correlation of ˜ϕ(x) over long distances decays over long

times. In order to establish the diverging of the correlation S

(q) in the small-q limit, we

make use of the Schwarz inequality (Dennery and Krzwicki, 1967)

(q)S

(q) ≥|S

(q)|

, (5.4.12)

where S

, S

, and S

are the static correlations between two variables A(q) and

B(q), with S

(q) =A(q)B(q) etc. In particular, we make the choice A(q) = ϕ

and

B(q) =˙a(q). The diagonal elements of the static correlation matrix are now obtained as

= S

(q), (5.4.13)

= q

(q). (5.4.14)

The susceptibility S

(q) =

, which follows from the continuity eqn. (5.4.4). Since

B(q) =˙a(q, t) =−{H, a(q, t)} (5.4.15)

the susceptibility S

is obtained as

=−ϕ

˙a(−q)=ϕ

{H, a(−q, t)}. (5.4.16)

We use the following result involving the Poisson bracket (the proof is given in the appendix

to this chapter):

=ϕ

{H, a(−q)} = β

−1

{ϕ

, a(−q)}. (5.4.17)

Since we are interested in the small-q limit, the equilibrium average on the RHS of (5.4.17)

is obtained as

lim

q→0

{ϕ

, a(−q)} = V

−1



dx dy{˜ϕ(x), a(y)}

={˜ϕ(x), Q}, (5.4.18)

assuming that the equilibrium average { ˜ϕ(x), Q} is independent of x. Using the condition

(5.4.5), the average of the Poisson bracket is expressed in terms of the longitudinal part of

the order parameter,

{˜ϕ(x), Q} = ξ

ψ(x)≡ξ

(5.4.19)

(say). Now, using the Schwarz inequality (5.4.12), we obtain

lim

q→0

(q) ≥

, (5.4.20)

where κ = (k

T ξ

)

(0). In the absence of any long-range force in the system, S

(0)

remains bounded.

5.4 Hydrodynamics of a solid 249

Goldstone modes in a crystal

The order-parameter ﬁeld for the crystalline state with inhomogeneous density ρ(x) is con-

structed to be proportional to δρ (x) = ρ(x) −ρ

. The order-parameter ﬁeld corresponding

to the RLV K is deﬁned as

(x) =[ρ(x) − ρ

]cos(K · x), (5.4.21)

where ρ

is the equilibrium density in the homogeneous liquid state. It is obvious that

the above deﬁnition ensures that the crystal symmetry is maintained in the order parameter

(x) = ψ

(x+R), where R is the lattice vector for the crystal. The continuous symmetry

which is broken when the liquid freezes into a crystal is the translational invariance. The

generator of the symmetry in this case is the total momentum Q ≡ P and the corresponding

density a(x) ≡ g(x),

P(x) =



dxg(x). (5.4.22)

Now, we need to ﬁnd the third ﬁeld ˜ϕ

(x), which forms a triad with ψ

(x) and g(x)

satisfying the commutation relation (5.4.5). We deﬁne

˜ϕ

(x) ≡ u

(x) = ρ(x)

sin(K · x)

(5.4.23)

and consider the Poisson bracket

(x), P

sin(K · x)

{ρ(x), P

}. (5.4.24)

We now adopt the deﬁnitions (5.1.1) and (5.1.2) for the density and the momentum density.

Using the fundamental Poisson bracket (Landau and Lifshitz, 1975a) it is straightforward

to obtain

{ρ(x), P





{ρ(x), g

(x)}=−∇

ρ(x). (5.4.25)

Using eqn. (5.4.25) in the result (5.4.24) gives

(x), P

}=−

sin(K · x)

∇

ρ(x)

cos(K · x)[ρ(x) − ρ

]−∇



sin(K · x)

δρ (x)



(x) −∇



sin(K · x)

δρ (x)



. (5.4.26)

Taking the Fourier transform of eqn. (5.4.26), we write to leading order in the wave vector

q the Poisson-bracket relation similar to the form (5.4.5),

(q), P

(q). (5.4.27)

We can therefore interpret ψ

(q) as the order-parameter ﬁeld for the crystal and u

(q)

as the new slow variable representing the Nambu–Goldstone modes. We attach the αth

250 Dynamics of collective modes

(α = 1,...,N ) particle to a parent lattice denoted by R

displaced by a distance u

(t)

from it such that

(t) = R

+ u

(t). (5.4.28)

Then, using eqn. (5.4.28) in the expression (5.4.23), we obtain

(x) =



sin



K ·



+ u



δ(x − r

(t))



sin(K · u

)

(

x − R

(t)

)

K ·



(t)δ

(

x − R

(t)

)

+ O(u

), (5.4.29)

wherewehaveusedsin



K · R



= 0 in reaching the last equality.

If the





represent a regular crystalline lattice and K the corresponding RLVs, this

holds by deﬁnition. If the





represent a random structure for an amorphous solid, this

holds only locally for large K. Assuming that the displacements u

(t) are small, the above

deﬁnition for u

(x) reduces to the longitudinal component of the so-called displacement

vector u(x, t), which is deﬁned in terms of the displacement of the particles around their

respective parent sites as follows:

u(x, t) =



(t)δ

(

x − R

)

, (5.4.30)

so that u

(x) = n

K · u (x).Hereρ

= mn

is the average density with n

= N/V

being the average number of particles per unit volume. The extra slow mode for the crystal

is therefore the displacement ﬁeld u(x, t ). If we ignore the presence of vacancies in the

crystal, we can attach every particle (α) to its corresponding parent lattice site at R

and

its location is then described in terms of its displacement u

from the parent site. With

this assumption of zero vacancy density, the number of lattice sites is equal to that of the

particles. We write the inhomogeneous density function ρ(x, t ) in the form

ρ(x, t) =



α=1

mδ(x − r

(t)) =



α=1

mδ

(

x − R

− u

(t)

)



α=1

mδ

(

x − R

)



(t) · ∇

(

x − R

= ρ

(x) − ρ

∇ · u(x). (5.4.31)

Therefore the density ﬂuctuation at a given point in the solid is simply the divergence of

the displacement ﬁeld, i.e., δρ ≡−ρ

∇ · u(x). For a crystal in which defects are present,

this relation no longer holds. The difference of these two quantities has been often treated