Dake L.P. Fundamentals of reservoir engineering

Подождите немного. Документ загружается.

REAL GAS FLOW: GAS WELL TESTING 251

8.5 COMPARISON OF THE PRESSURE SQUARED AND PSEUDO PRESSURE

SOLUTION TECHNIQUES

Much has been written

3,4,5

about the conditions under which the p

and m(p) solution

techniques give identical results. Comparison of the methods can best be summarised

by directly comparing equ. (8.5) and equ. (8.15) i.e.

when is

−

equivalent to

()

pdp

mp mp 2

−=

()()

wf wf

pp pp

+−

equivalent to

pdp

(8.17)

where both

and Z appearing on the left hand side are evaluated at

(p p ) / 2+ . As

shown in fig. 8.6, the equivalence expressed in equ. (8.17) is only established if p

/Z is

a linear function of the pressure.

Pressure

Fig. 8.6 p/µZ as a linear function of pressure

In this case the area under the curve between p and p

is the integral in equ. (8.17),

which is equal to

()

⋅−

However, in general p/

Z is non-linear and has the typical shape shown in fig. 8.7.

It can be seen that p/

Z versus p is only linear at high and very low pressures, the

latter corresponding to the ideal gas state. In between, there is a very definite curved

section in the plot where the two different solution techniques are liable to give different

results.

REAL GAS FLOW: GAS WELL TESTING 252

∆

Pressure

Fig. 8.7 Typical plot of p/µZ as a function of pressure

The diagram also shows that even in the non-linear part of the plot, providing the

drawdown,

pp dp,−= is small, the two methods will always give approximately the

same answers. It is only when the drawdown is very large (i.e. for low kh reservoirs

producing at high rates) that the results using the two methods will be significantly

different. Under these circumstances the assumption implicit in the Russell Goodrich

approach, namely that pressure gradients are small, is no longer valid.

With the exception of the brief description of the history of gas well testing in sec. 8.10,

all the equations for the flow of a real gas, in the remainder of this chapter, will be

expressed in terms of real gas pseudo pressures. The reasons for adopting this

approach are:

- it is theoretically the better method and in using it one does not have to be

concerned about the pressure ranges in which it is applicable, as is the case when

using the p

method

- with a bit of practice, it is technically the more simple method to use once the basic

relationship for m(p) as a function of p has been derived

- the necessity for iteration in solving the inflow equation for p

is avoided

- the technique is widely used in the current literature and readers are expected to be

quite familiar with its application.

8.6 NON-DARCY FLOW

For the horizontal flow of fluids through a porous medium at low and moderate rates,

the pressure drop in the direction of flow is proportional to the fluid velocity. The

mathematical statement of this relationship is Darcy's law, which for radial flow is

dr k

= (8.18)

where u is the fluid velocity =

2rh

⋅

REAL GAS FLOW: GAS WELL TESTING 253

At higher flow rates, in addition to the viscous force component represented by Darcy's

equation, there is also an inertial force acting due to convective accelerations of the

fluid particles in passing through the pore spaces

. Under these circumstances the

appropriate flow equation is that of Forchheimer (1901), which is

dr k

βρ

=+ (8.19)

In this equation the first term on the right hand side is the Darcy or viscous component

while the second is the non-Darcy component. In this latter term,

is the coefficient of

intertial resistance and, as the following dimensional analysis shows, has the

dimension (length)

-1

[]

22 3 2

dp ML 1 M L

dr LTL L T

βρ

éùéù éù

êúêú êú

ëûëû ëû

−

The non-Darcy component in equ. (8.19) is negligible at low flow velocities and is

generally omitted from liquid flow equations. For a given pressure drawdown, however,

the velocity of gas is at least an order of magnitude greater than for oil, due to the low

viscosity of the former, and the non-Darcy component is therefore always included in

equations describing the flow of a real gas through a porous medium.

Because of this it should be necessary to use the Forchheimer equation, rather than

that of Darcy, in deriving the basic radial differential equation for gas flow (refer

Chapter 5, sec. 2). Fortunately, even for gas, the non-Darcy component in equ. (8.19)

is significant only in the restricted region of high pressure drawdown, and flow velocity,

close to the wellbore.

Therefore, the non-Darcy flow is conventionally included in the flow equations as an

additional skin factor, that is, as a time independent perturbation affecting the solutions

of the basic differential equation in the same manner as the van Everdingen skin

(Chapter 4, sec. 7). Forchheimer's equation was originally derived for the flow of fluids

in pipes where at high velocity there is a distinct transition from laminar to turbulent

flow. In fluid flow in a porous medium, however, for most practical cases in reservoir

engineering, the macroscopic flow is always laminar according to the definitions of

classical fluid dynamics. What is referred to as the non-Darcy component does not

correspond with classical ideas of turbulent flow but, as stated earlier, is due to the

accelerations and decelerations of the fluid particles in passing through the pore

spaces. Nevertheless, Forchheimer's equation can be used to describe the additional

pressure drop due to this phenomenon, by integrating the second term on the right

hand side of equ. (8.19), as follows.

non Darcy

pdr

2rh

βρ

æö

∆=

ç÷

èø

or expressed as a drop in the real gas pseudo pressure, using equ. (8.8)

REAL GAS FLOW: GAS WELL TESTING 254

()

2p q

mp dr

2rh

βρ

µπ

æö

∆=

ç÷

èø

(8.20)

Also since

= γ

× density of air at s.c. × E

constant

=××

ΖΤ

where γ

is the gas gravity (air=1)

Then equ. (8.20) can be written as

()

m p constant dr

æö

∆= ×

ç÷

ΖΤ

èø

(8.21)

and since

sc sc

constant q

== ×

ΖΤ

then for isothermal reservoir depletion equ. (8.21) becomes

()

gsc

mp constant

βγ

∆= ×

(8.22)

Since non-Darcy flow is usually confined to a localised region around the wellbore

where the flow velocity is greatest, the viscosity term in the integrand of equ. (8.22) is

usually evaluated at the bottom hole flowing pressure p

and hence is not a function of

position. Integrating equ. (8.22) gives

()

gsc

mp constant

rrh

βγ

æö

∆= × −

ç÷

èø

(8.23)

If equ. (8.23) is expressed in field units (Q - Mscf/d,

- ft

-1

) and assuming

,then

()

12 2

wpw

m p 3.161 10 FQ

βγ

−

∆=× =

(8.24)

where F is the non-Darcy flow coefficient psia

/cp/(Mscf/d)

Since non-Darcy flow is only significant very close to the wellbore, two assumptions are

commonly made in connection with equ. (8.24), these are

- the value of the thickness h is conventionally taken as h

, the perforated interval

of the well

- the pseudo pressure drop ∆m(p)

= FQ

can be considered as a perturbation

which readjusts instantaneously after a change in the production rate.

REAL GAS FLOW: GAS WELL TESTING 255

Because of the latter assumption the FQ

term can be included in equs. (8.15) and

(8.16) in very much the same way as the mechanical skin factor, only in this case it is

interpreted as being a rate dependent skin. Thus equ. (8.15), for instance, including the

non-Darcy flow component, becomes

()

1422 TQ 3

mp mp ln S FQ

kh r 4

æö

−= −++

ç÷

èø

(8.25)

1422 TQ 3

ln S DQ

kh r 4

æö

=−++

ç÷

èø

(8.26)

where in the latter expression, which is commonly used in the literature, DQ is

interpreted as the rate dependent skin factor and

Fkh

1422T

= (8.27)

Either F or D is used in the remainder of this chapter, to allow for non-Darcy flow,

depending on which is the more convenient for the application being considered.

8.7 DETERMINATION OF THE NON-DARCY COEFFICIENT F

Two methods are available for the determination of the non-Darcy flow coefficient,

which are

- from the analysis of well tests

- by experimentally measuring the values of the coefficient of inertial resistance,

β and using it in equ. (8.24) to calculate F.

Of these two, the well testing method will give the more reliable result just as in the

case of oil well testing in which, from the slope of the pressure buildup plot, a more

meaningful value of the kh product can be obtained than by measuring values of the

permeability on a selection of core samples and trying to average these results over

the entire formation. Furthermore, in the well test F will be measured in the presence of

any liquid saturation in the vicinity of the well. The determination of F by well testing will

be described in detail in secs. 8.10 and 8.11 and will not be discussed further at this

stage.

To determine

experimentally, the procedure is to first measure the absolute

permeability of each of the core samples and then to apply a series of increasing

pressure differentials across each sample by flowing air through the core plugs at ever

increasing rates. Knowing the flow rates and pressure differentials across the plugs,

the coefficient of inertial resistance can be directly calculated using a linear version of

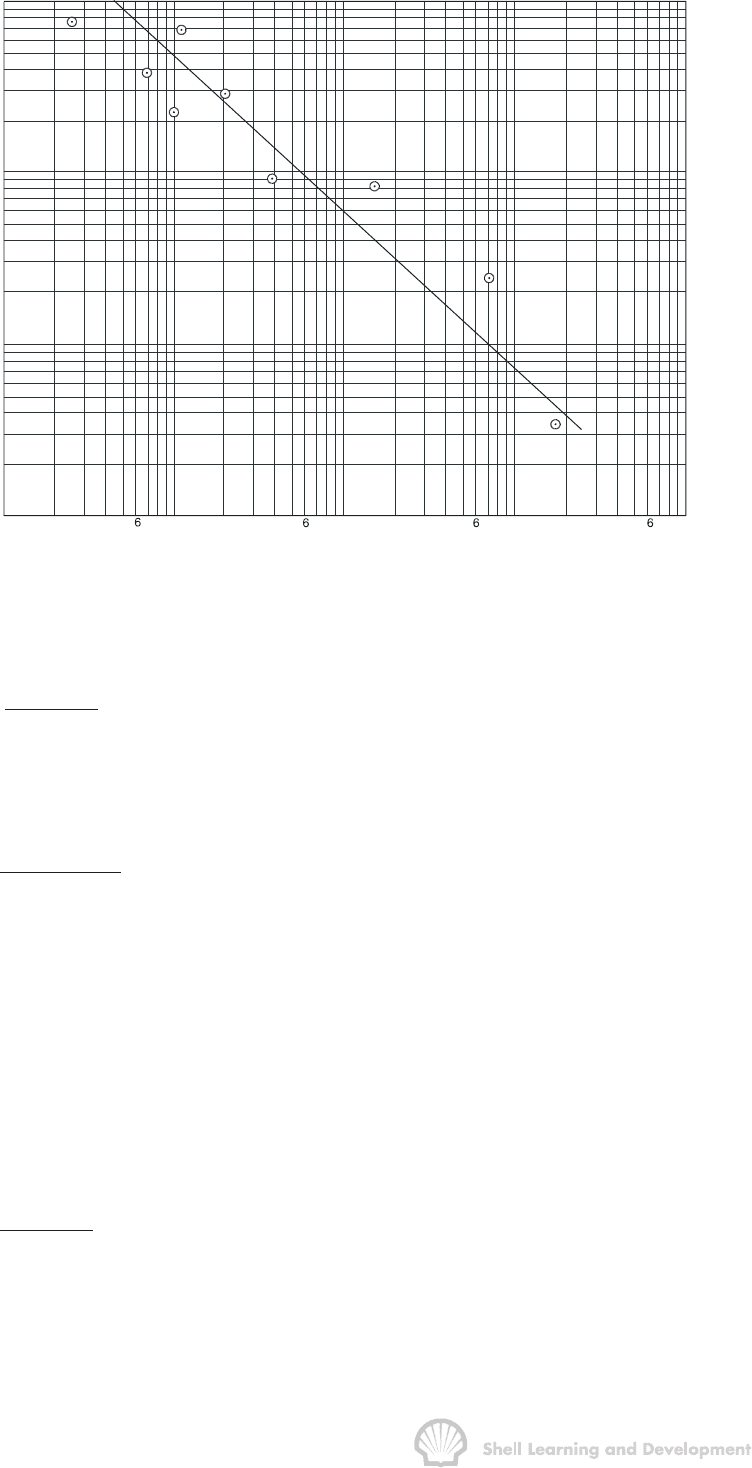
the Forchheimer equation (8.19). The results are usually presented as shown in fig. 8.8

in which

is plotted as a function of the absolute permeability over the range of core

samples tested.

REAL GAS FLOW: GAS WELL TESTING 256

234

2345

789 2 3 4 5 789 2 3 4 5 789

- FACTOR (1/cm)

(

)

Fig. 8.8 Laboratory determined relationship between

ββ

and the absolute permeability

A relationship is usually derived of the form

cons tan t

= (8.28)

in which the exponent

is a constant. For the experimental results shown in fig. 8.8 the

specific relationship is

1.1045

2.73 10

where k is in mD and β in ft

-1

. Providing that the range of porosity variation in the

samples is not too great, the variation of β with

can be neglected in comparison with

the variation of β with the absolute permeability.

The experimental value of β so determined is applicable to the flow of gas at 100%

saturation. In the presence of a liquid saturation, e.g. connate water and immobile

liquid condensate, Gewers, Nichol and Wong

7,8

have experimentally determined that

the permeability term in equ. (8.28) should be replaced by the effective permeability to

gas at the particular liquid saturation S

, thus

()

cons tan t

= (8.29)

It should be noted that the experimental work of Gewers, Nichol and Wong, in directly

measuring β in the presence of a liquid saturation, was conducted on microvugular

carbonate rock samples for which the dry core β values are at least an order of

REAL GAS FLOW: GAS WELL TESTING 257

magnitude greater than for typical sandstone samples. So far, the experiments have

not been repeated on sandstone but in using equ. (8.29) it is assumed that the same

physical principles will apply. Although correlation charts giving β as a function of the

permeability exist in the literature

the reader should be aware that they are not always

applicable. Irregularities in the pores can greatly modify the β versus k relationship

making it advisable, in many cases, to experimentally derive a relationship of the form

given by equ. (8.28).

8.8 THE CONSTANT TERMINAL RATE SOLUTION FOR THE FLOW OF A REAL GAS

The constant terminal rate solution of the radial diffusivity equation

() ()

mp mp

rr r k t

φµ

æö

∂∂

∂

ç÷

∂∂ ∂

èø

(8.11)

for the flow of a real gas, describes the change in real gas pseudo pressure at the

wellbore due to production at a constant rate from time t = 0. Equation (8.11) is

identical in form with equ. (5.20) except that pseudo pressure replaces real pressure as

the dependent variable. Therefore, the constant terminal rate solution of equ. (8.11)

must, by analogy, have the same form as the solution presented for liquid flow in

Chapter 7.

For small flowing times, the transient, constant terminal rate solution of equ. (8.11), in

Darcy units, is similar to equ. (7.10), i.e.

() ( )

iwf

4kt

mp mp constant ln 2S

γφµ

æö

′

−= ×⋅+

ç÷

èø

in which S' = S + DQ. The constant can be evaluated using the relationship

()

mp p

∆=∆

therefore,

() ( )

iwf

2p q 4 kt

mp mp ln 2S

4kh cr

µπ γφµ

æö

′

−= +

ç÷

èø

and converting to field units, using the fact that pq/Z = (p

)T/T

, gives

() ( )

iwf

4t711QT

mp mp ln 2S

æö

′

−= +

ç÷

èø

(8.30)

Taking the analogy with the liquid flow equations a stage further, equ. (8.30) can be

expressed in dimensionless form as

() ( )

()

iwfDD

mp mp m t S

1422QT

′

−=+

(8.31)

REAL GAS FLOW: GAS WELL TESTING 258

in which m

) is the dimensionless real gas pseudo pressure which for transient flow

conditions is simply

()

mt ln

(8.32)

and is identical in form to equ. (7.23).

Similarly, for long flowing times the semi-steady state constant terminal rate solution of

equ. (8.11), in Darcy units, is

() ( )

iwf

2p q 4A kt

mp mp ln 2 S

2kh cACr

µπ φµγ

æö

′

−= + +

ç÷

èø

which is the equivalent of equ. (7.13). In field units this becomes

() ( )

iwf DA

1422QT 4A

mp mp ln 2 t S

kh C r

æö

′

−= + +

ç÷

èø

and therefore the m

) function for semi-steady state flow is

()

DD DA

mt ln 2 t

(8.33)

which is equivalent to equ. (7.27).

To generalise, the dimensionless real gas pseudo pressures are the constant terminal

rate solutions of the equation

DD D D

rr r t

æö

∂∂

∂

ç÷

∂∂∂

èø

(8.34)

and the solution which is valid for all values of the flowing time is

()

D D DA DA

DMBH

mt 2 t ln m t

=+ −

(8.35)

which is the same as equ. (7.42), for liquid flow.

The m

D(MBH)

function, the Matthews, Brons and Hazebroek dimensionless pseudo

pressure, can be read directly from the MBH charts, figs. 7.11-15, for the appropriate

value of the dimensionless time argument t

, in just the same way as the p

D(MBH)

function was evaluated for use in equ. (7.42). Since field units are being used in this

chapter, the abscissa and ordinate of the MBH charts should be interpreted as

()

kt hrs

t 0.000264

φµ

(8.36)

and

REAL GAS FLOW: GAS WELL TESTING 259

()

DMBH

m t mp mp

711QT

æö

=−

ç÷

èø

(8.37)

The right hand side of equ. (8.37) is only used to calculate

()

mp, having already

determined m(p

) from the extrapolated pseudo pressure buildup plot (ref. sec. 8.11).

In the majority of cases, m

D(MBH)

is simply a number read from the MBH charts for the

appropriate value of t

, for use in equ. (8.35).

Because of the equivalence in form of the constant terminal rate solution for both oil

and gas, when expressed in dimensionless parameters, there is no need to elaborate

further on how this solution is used in practice since the subject has been fully

described in the previous chapter. The application of equ. (8.35) to gas well testing will

be demonstrated in secs. 8.10 and 11.

Although the form of the m

and p

functions is the same, it must always be kept in

mind that the m

function applied to real gas flow is less accurate than the p

function

applied to liquid flow. The reason is that the m

functions are derived as solutions of

equ. (8.11), which is non-linear. The non-linearity arises from the fact that both the real

gas viscosity and compressibility in the coefficient

µc/k, in equ. (8.11),are highly

pressure dependent. Fortunately, the gas viscosity is directly proportional to the

pressure while the compressibility, equ. (1.31), is inversely proportional to pressure and

this tends to reduce the pressure dependence of the product.

This favourable effect is particularly pronounced in the high pressure range where the

product is fairly constant. For instance, using the PVT data presented in table 8.1, the

value of µc only increases from 3.54 × 10

-6

cp/psi at 4400 psia to 4.96 x 10

-6

cp/psi at

3400 psia. In evaluating these figures, the isothermal gas compressibility has been

calculated using equ. (1.31), treating the pore and connate water compressibilities as

negligible in comparison to that of the gas. This practice is adhered to in the remainder

of this chapter, thus c

≈ c

= c.

Because of this insensitivity of the µc product to pressure change it is common, when

applying the m

function, to use the product (µc)

evaluated at the initial equilibrium

pressure, which is also the assumption made in generating p

functions for liquid flow.

Thus, t

, t

and 1/2 m

D(MBH )

) in equ. (8.35), which are dependent on the product,

are all evaluated using (µc);. Al-Hussainy, Ramey and Crawford

have demonstrated

that, using this initial value of the product, the m

functions do correlate very favourably

with the p

functions for liquid flow over a wide range of conditions. While the match is

very good for transient flow conditions, it is less reliable for very large values of the

flowing time, once the boundary effects have been felt. Thus, equ. (8.32) correlates

with the p

function better than equ. (8.33). The latter must, therefore, be used with

more caution. Fortunately, the inflow equation (8.15), for semi-steady state flow, which

can be expressed in dimensionless form as

()

wf D

kh 4A

mp mp m t S ln S

1422QT

′′

−=+= +

(8.38)

REAL GAS FLOW: GAS WELL TESTING 260

was found to correlate almost exactly with the equivalent function for liquid flow for all

values of the flowing time. This is to be expected since the, µc product is not present in

equ. (8.38) as a result of the use of pseudo pressures, rather than pressures, in its

formulation. The correlations between m

and p

functions were only checked for a well

producing at the centre of a circular shaped reservoir, equs. (8.35) and (8.38) are

generalized expressions which include the dependence of m

on geometry and well

asymmetry.

In practice, one is interested in applying the constant terminal rate solution

function) to the analysis of well tests and several examples of such usage are

provided in the following sections of this chapter. All the examples considered are for

initial well tests and, for this condition, the evaluation of the m

function using the (µc)

product can be expected to be quite reliable, particularly if the test duration is not

excessively long and the pressure drawdowns imposed are not too large. Problems

arise, however, when analysing routine pressure surveys throughout the producing

lifetime of the reservoir. For instance, if a pressure test is conducted in a well several

years after the start of production, at what pressure should the µc product be

evaluated? This question will be dealt with in sec. 8.11 using the method presented by

Kazemi

, which describes how the average reservoir pressure can be obtained from a

pressure analysis using a µc product which must be iteratively determined. Once the

average reservoir pressure is known, however, the inflow equation (8.38) can be used

with confidence to calculate the long term deliverability of wells.

8.9 GENERAL THEORY OF GAS WELL TESTING

Gas well tests can be interpreted using the following equations

()

nnj1

iwf jDDDnn

mp mp Q m t t QS

1422T

−

′

−=∆ −+

(8.39)

in which

()

nj1

DD D DD DA DA

DMBH

jjj1

mt t mt 2t ln m t

QQQ

and

SSDQ

−

′

′′ ′

−= = + −

∆=−

′

(8.40)

For convenience, equ. (8.39) is frequently expressed in the form

()

nnj1

iwfn jDDDn

mp mp FQ Qm t t QS

1422T

−

−−=∆ −+

(8.41)

in which F is the non-Darcy flow coefficient, equ. (8.27).

These equations are analogous to equs. (7.31) and (7.42) which were used for oilwell

test analysis. Equation (8.39) results from the application of the principle of

superposition in time, as described in Chapter 7, sec. 5. In the summation of the