Dake L.P. Fundamentals of reservoir engineering

Подождите немного. Документ загружается.

REAL GAS FLOW: GAS WELL TESTING 261

individual constant terminal rate solutions it is assumed that the only skin factor term

remaining which influences p

is the value Sn

′

= S + DQn. This is because the rate

dependent skin factor is not, in itself, a time dependent solution of the diffusivity

equation but is merely considered to have a perturbing influence on the bottom hole

flowing pressure which re-adjusts instantaneously when the rate changes. Thus, even

though the DQ terms in the summation leading to equ. (8.39) do not algebraically

cancel, as do the mechanical skin factor components, on changing the rate from Q´

n-1

to Q

the value of

p is only influenced by DQ

. The components DQ

n-1

, DQ

n-2

. . .

n-j

have no transient effects and die out immediately.

The main difference between oil and gas well testing arises from the fact that the total

skin factor in a gas well has two components, one of which is rate dependent. Because

of this, a gas well must be tested with a minimum of two separate flow rates to be able

to differentiate between these two skins.

Thus, at rate Q

the total skin

SSDQ

′

can be obtained from the test analysis, while at rate Q

SSDQ

′

can be similarly determined. The two equations for

′

, and

′

can then be solved

simultaneously to provide S and D (or F).

A further complication in applying equs. (8.39) and (8.40) to gas well test analysis lies

in the fact that the superposition principle itself, which is implicit in the formulation of

equ. (8.39), is strictly only valid when applied to solutions of linear differential

equations. Since it is the constant terminal rate solution of the non-linear radial

diffusivity equation (8.11) that is being superposed, some fundamental mathematical

error might therefore be expected. Al-Hussainy, Ramey and Crawford

have shown, by

comparing superposed m

functions for gas with the superposed p

functions for liquid

flow, that the error is very slight providing that the test is conducted with an increasing

rather than a decreasing rate sequence.

As stated in sec. 8.8, the viscosity-compressibility product used in an initial well test is

(µc)

evaluated for the initial equilibrium pressure p

. In the test analysis exercises

included in the following sections of the chapter, the initial pressure in each case is

taken as 4290 psi and the PVT data and real gas pseudo pressures of table 8.1 are

common to all. The value of (µc)

under these circumstances is 3.6 × 10

-6

cp/psi and no

allowance for its variation is made during the ensuing analyses. It is interesting to note

that, in spite of the high compressibility, the µc product for a gas reservoir (

≈

µc

) is

invariably three or four times smaller than for an oil reservoir, because of the low

viscosity of the gas. This implies that, for a given drainage area, permeability and

porosity, the change from transient to either late transient or stabilized flow can be

expected to occur much more rapidly in a gas than in an oil reservoir. This has

implications which will be discussed in greater detail in secs. 8.10 and 8.11.

REAL GAS FLOW: GAS WELL TESTING 262

In conclusion, it can be stated that the use of equs. (8.39) and (8.40) to analyse gas

well tests is never quite as satisfactory as using the combination of equs. (7.31) and

(7.42) for oilwell tests. Nevertheless, the former equations do provide what is usually

described in the literature as "a reasonable engineering approximation" and their

application will now be described in detail.

8.10 MULTI-RATE TESTING OF GAS WELLS

This section will be presented in the form of a brief history of the subject of multirate

testing of gas wells in which former analysis techniques will be compared with the

method implied in the use of equ. (8.39) and (8.40).

The first and perhaps the best known equation for analysing multi-rate tests is that of

Schellhardt and Rawlins

which was empirically established as the result of the

analysis of some 600 gas well tests during the 1930's. The equation is

()

iwf

QCp p=− (8.42)

"back pressure equation". Using the observed pressures at the end of each flow period

a plot can be made of log

iwf

(p p )− versus log Q, the slope of which has the value 1/n.

Having thus determined n, the value of C can be calculated using equ. (8.42).

It was originally believed that both C and n were constants that, once determined from

the test analysis, could be used for the long term prediction of gas well deliverability.

This being accomplished merely by replacing p

by the current average reservoir

pressure

p . Carter et al.

, have shown, however, that n is a variable with a range

between .5 and 1 depending on whether the value of the non-Darcy flow component

, defined by equ. (8.24), is very large (n = .5) or negligible (n = 1). Furthermore, the

value of C can be shown to be dependent on k, A, C

and S and also on the pressure

dependent functions,

, Z and the flowing time, and can hardly be expected to remain

constant throughout the producing life of the well. These statements will not be

substantiated in this text since it is not intended to use equ. (8.42) which may be

regarded, at best, as being a useful empirical approximation.

Nevertheless, in spite of all the drawbacks mentioned above, it was found that the back

pressure equation could be used with tolerable accuracy in analysing tests in which it

was suspected that semi-steady state flow conditions prevailed during each separate

flow period. As a result, it became, and still is, quite fashionable to test wells in such a

way that stabilized flow is achieved at each rate. Precisely when the change from

transient to semi-steady state flow occurs depends on some minimum value of

= .000264 kt/

(

A, (a fact which is clearly illustrated by the MBH charts,

figs. 7.11-15), which in turn depends upon the geometry of the drainage area and well

asymmetry. As already noted in sec. 8.8, since the

c product for gas is considerably

smaller than for a liquid, there is at least some justification in attempting to analyse gas

well tests assuming stabilized flow conditions, even for a test of relatively short

duration.

REAL GAS FLOW: GAS WELL TESTING 263

The most popular current method of analysing such a test is to use the semi-steady

state inflow equation, (8.38), which, including both skin factor components and

assuming that for an initial test p = p

, becomes

() ( )

iwf

1422QT 4A

mp mp ln S FQ

kh C r

æö

−= ++

ç÷

èø

(8.43)

which can be further simplified as

() ( )

iwf

mp mp BQ FQ−=+ (8.44)

where B is the Darcy coefficient and F the non-Darcy coefficient of the inflow equation.

The purpose of testing is then to determine B and F and to use these values for

predicting the future deliverability of the well, for which p

is replaced by the current

average pressure

p . The method of analysis is simply to plot

()

iwf

mp mp

versus Q

−

(8.45)

in which the Q

are the surface production rates and p

the values of the bottom hole

flowing pressure recorded at the end of each separate flow period. The plot should be

linear with slope F and intercept B, when Q

= 0; an example of such a plot is shown as

fig. 8.9.

This method of analysis is simple and the results obtained in terms of B and F are

considered more reliable parameters for estimating well deliverabilities than the

C and n determined using equ. (8.42).

Nevertheless, the application of the stabilized well inflow equation (8.43), to analyse a

well test is mathematically incorrect and the results obtained from such an analysis can

only be considered as an approximation, although, as will be demonstrated in

exercise 8.1, a perfectly acceptable approximation in many cases. The fault lies in

analysing the test data using an inflow equation rather than the superposed constant

terminal rate solutions, equ. (8.39). It may well be that each flow period in the test is

sufficiently long so that semi-steady state conditions prevail but that does not mean

that, for instance, the wellbore pressure response during the third flow period is

unaffected by what happened during the first and second periods, as implied by the

use of equ. (8.43) in the analysis.

The rigorously correct technique is to use equ. (8.39) in which the m

functions,

equ. (8.40), are evaluated for semi-steady state flow as

()

DDA DA

mt ln 2 t

′′

(8.33)

The test analysis equation is then

REAL GAS FLOW: GAS WELL TESTING 264

()

nnj1

i wf j DA DA n n

kh 4A

m(p ) m(p ) Q 2 (t t ) Q ln S DQ

1422T C r

−

æö

−=∆ −+ ++

ç÷

èø

or alternatively, by re-arranging the summation term

()

iwf jDAn n

kh 4A

m(p ) m(p ) 2 Q t Q ln S DQ

1422T C r

æö

−= ∆+ ++

ç÷

èø

where

jj1

DA DA DA

ttt

−

∆= −

Finally, dividing throughout by Q

, converting to real time (hours) and taking the rate

dependent skin over to the left hand side of the equation gives

()

iwfn

nnAw

m(p ) m(p ) FQ

2.359T 1422T 4A

tlnS

QcAhQkhCr

φµ γ

−−

æö

=∆+ +

ç÷

èø

(8.46)

It can be seen immediately, from this equation, that if the first term on the right hand

side is ignored then it reduces to exactly the same form as the semi-steady state inflow

equation, (8.43). The additional term

()

2.539T

cAh Q

φµ

∆

can be interpreted as a material balance correction required due to the use of the initial

pressure p

in the inflow equation, (8.43), rather than the current average pressure

which, for t > 0, is somewhat lower and changes throughout the test. Therefore, the

difference between equ. (8.46) and (8.43) is generally rather small, especially in cases

of interest, that is, large gas accumulations (large Ah

). Theoretically, a plot of

iwfn

m(p ) m(p ) FQ

versus t

−−

∆

(8.47)

should be linear with slope

() ()

2.359T 2.359T

c Ah c Pore Volume

φµ µ

and intercept

1422T 4A

BlnS

kh C r

æö

ç÷

èø

Of course, to draw this plot requires a knowledge of the non-Darcy flow coefficient F.

As a starting point the value of F determined as the slope of the plot of equ. (8.45) can

be used and the value decreased gradually until the plot of equ. (8.47) becomes linear.

The slope of the latter plot will then yield the value of the pore volume and the intercept

REAL GAS FLOW: GAS WELL TESTING 265

the correct value of the Darcy flow coefficient B. At first sight this analysis technique

appears to be rather useful but the following exercise will reveal the great sensitivity in

the plot to the chosen value of F.

EXERCISE 8.1 MULTI-RATE GAS WELL TEST ANALYSED ASSUMING

STABILIZED FLOW CONDITIONS

A gas well is tested by producing it at four different rates over a total period of

48 hours. The rate-time sequence and pressures recorded at the end of each separate

flow period are listed in table 8.2.

Rate (Q)

Mscf/d

Cum. Flowing time

(t)

hrs

psia

m (p

)

psia

/cp

10 × 10

12 4182 1030.96 × 10

20 " 24 4047 984.29 "

30 " 36 3884 927.94 "

40 " 48 3694 862.26 "

TABLE 8.2

The reservoir temperature and fluid properties are the same as those listed in table 8.1

and therefore, the relationship between real pressure and pseudo pressure, fig. 8.3,

can be used in this exercise. For pressures in excess of 2800 psia, this relationship is

almost linear and can be matched by the equation

m(p) = (0.3457p — 414.76) × 10

psia

/cp (8.48)

from which the real gas pseudo pressures, m(p

), in table 8.2 have been calculated.

The reservoir and well data for the exercise are as follows

= 4290 psi h = 40 ft

(µc)

= 3.6 × 10

-6

cp/psi r

= 0.3 ft

If the correct values of the flow coefficients are

B = 3176 psia

/cp/Mscf/d and F = .04 psia

/cp/(Mscf/d)

1. Calculate both B and F using the interpretation technique suggested by equ. (8.45).

2. If there is a possible error of 10 psi in the measurement of p

, determine the effect

of this error on the analysis.

3. It is proposed to produce this reservoir block at a plateau production rate of

5 MMscf/d down to some fixed minimum wellhead pressure. If the plateau rate can

be maintained until the average reservoir pressure has fallen to 1200 psi, calculate

the error in the estimate of the cumulative gas production, at this stage, due to

REAL GAS FLOW: GAS WELL TESTING 266

using the analysis results determined in the first part of this exercise, instead of the

correct values of B and F.

4. Using, as an initial estimate, the value of F determined in the first part of this

exercise, analyse the test data using the interpretation technique of equ. (8.47).

EXERCISE 8.1 SOLUTION

1) Values of ∆m(p)/Q

required for the plot, equ. (8.45), are listed in table 8.3, for

= 4290 psia; i.e. m(p

) = 1068.29×10

psia

/cp.

(m(p

) − m(p

) ) /Q

psia

/cp/Mscf/dQ

Mscf/d

= 4290 psia: p

= 4280 psia: p

= 4300 psia:

10 × 10

3733 3388 4079

20 " 4200 4028 4373

30 " 4678 4563 4794

40 " 5151 5065 5237

TABLE 8.3

The corresponding plot of ∆m(p)/Q

versus Q

is shown as fig. 8.9. The intercept and

slope of the straight line give

B = 3262 psia

/cp/Mscf/d

and F = 0.047 psia

/cp/(Mscf/d)

2) Also listed in table 8.3 and plotted in fig. 8.9 are values of ∆m(p)/Q

as a function of Q

for initial pressures differing by ± 10 psi from the measured value of 4290 psia.

i.e. p

= 4280 psia: m(p

) = 1064.84×10

psia

/cp

and p

= 4300 psia: m(p

) = 1071.75×10

psia

/cp

These plots exhibit quite a pronounced degree of curvature, even for the relatively

small error in the measured value of p

. Therefore, if the plot of equ. (8.45) appears to

be curved, rather than linear, it is first necessary to determine the correct value of p

, by

trial and error, to obtain a straight line.

3) The inflow equation, using the values of B and F determined in the first part of this

exercise is

()

p − m(p

) = 3262 Q + .047 Q

whereas, using the correct values

()

p − m(p

) = 3176 Q + .040 Q

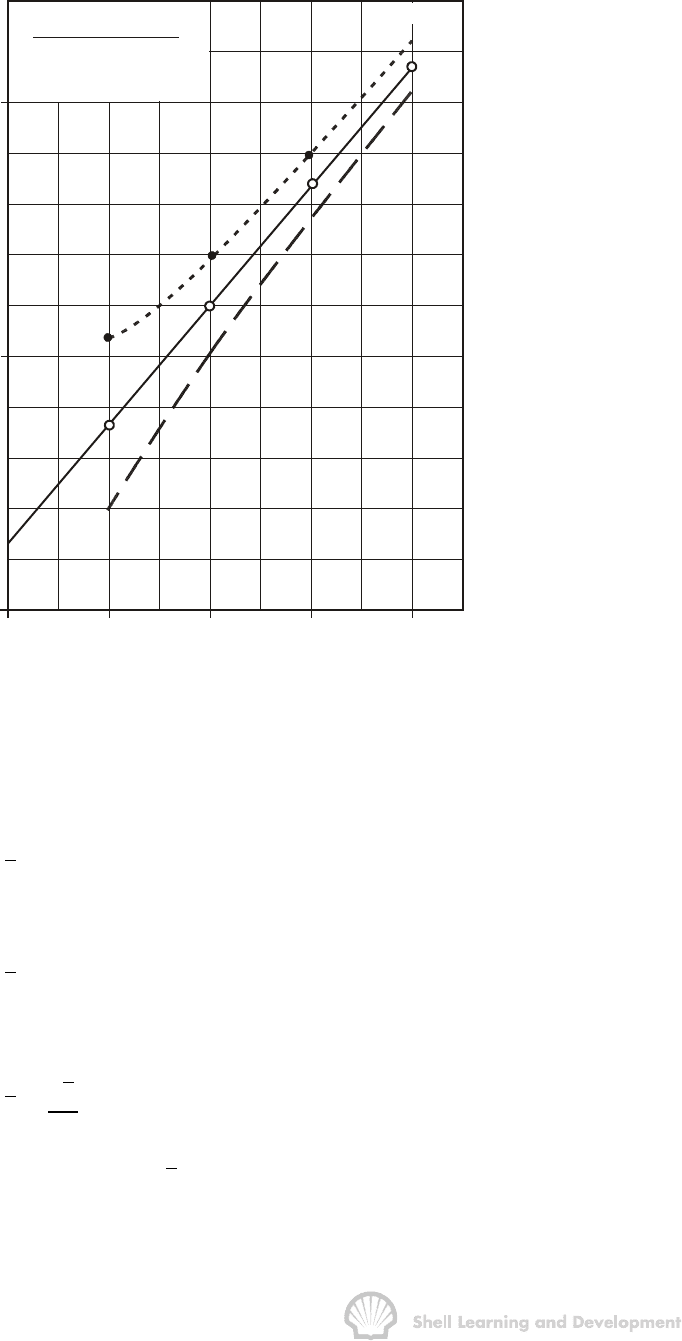
REAL GAS FLOW: GAS WELL TESTING 267

If it is assumed that these expressions will not change throughout the producing

lifetime of the well then, for a given plateau rate of 5 MMscf/d, the duration of the

plateau production is determined by the value of p

. If this pressure drops below the

level

5000

4000

3000

0 10 203040

Q (MMscf/d)

4300

4000

4290

4280

iwf

m(p) m(p )

−

(psia / cp / Mscf/d)

p (psia)

Fig. 8.9 Gas well test analysis assuming semi-steady state conditions during each

flow period. Data; table 8.3

required to maintain the minimum allowable wellhead pressure then the rate must be

reduced. Therefore, at this point the values of m(p

) in both the above equations must

be equal and

()

mp 86Q .007Q∆= +

and for Q = 5 MMscf/d

()

m p .605 10 psia / cp∆=×

Also

()

mp p

∆=∆

and using the data in table 8.1 for p = 1200 psi

REAL GAS FLOW: GAS WELL TESTING 268

.0153 .832 .605 10

p3.21psi

21200

×××

∆= =

Assuming a depletion type material balance, equ. (1.35), then

G()810G

p/Z

−

∆= ∆ ≈−×

Thus the use of the flow coefficients B and F, determined using the inflow equation in

the analysis is only very slightly pessimistic and in general provides a perfectly

acceptable approximation for highly productive wells such as the one described in this

exercise.

4) For the assumed value of F = .047 psia

/cp/(Mscf/d)

, which was determined in the first

part of this exercise, the data for the plot of equ. (8.47) are listed in table 8.4, and the

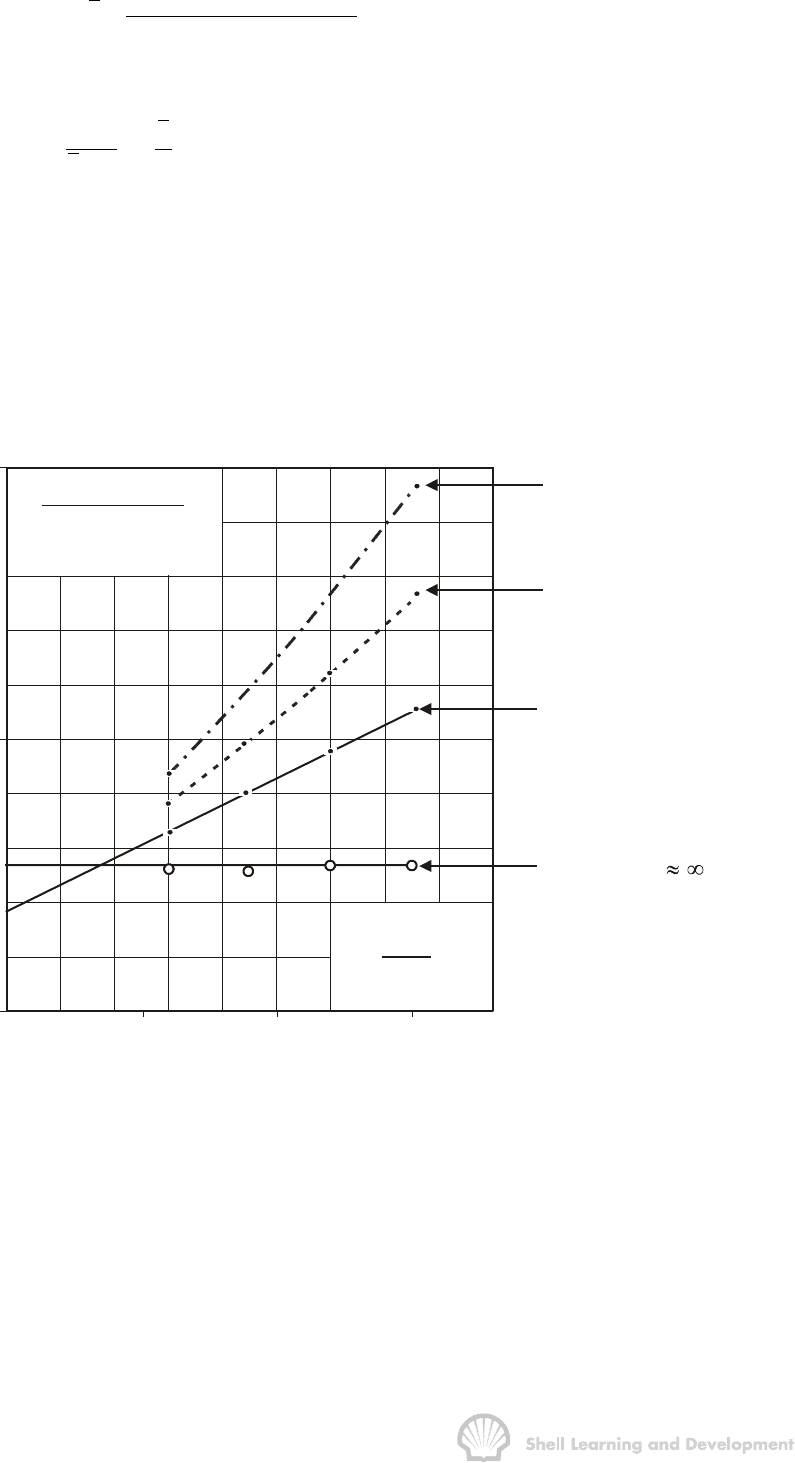
plot itself shown as fig. 8.10.

(psia / cp / Mscf/d)

m(p) FQ

∆−

4000

3500

3000

10 20

F = 0.047; A

∆

F = 0.035; A = 60 ACRES

F = 0.030; A = 43 ACRES

F = 0.040; A = 100 ACRE

Fig. 8.10 Gas well test analysis assuming semi-steady state conditions and applying

equ. (8.47). Data; table 8.4

REAL GAS FLOW: GAS WELL TESTING 269

psia

/cp/(Mscf/d)Q

Mscf/d

hrs

∆

hrs

()

mp FQ

∆−

F = .047

.03 .035 .04

10 × 10

12 12 3263 3433 3383 3333

20 " 24 18 3260 3600 3500 3400

30 " 36 24 3268 3778 3628 3478

40 " 48 30 3271 3951 3751 3551

TABLE 8.4

These data points plot almost as a horizontal straight line which implies an infinite area.

This is to be expected since the value of F determined in the first part of this exercise is

under the assumption that the reservoir pressure remains constant throughout the test,

which implicitly assumes that the reservoir is infinite.

The correct plot should have some positive slope corresponding to the fact that a finite

volume is being drained. This means that the value of F should be decreased on a trial

and error basis until a straight line is obtained. The plot has been re-drawn for values of

F of 0.040, 0.035 and 0.030, refer table 8.4 and fig. 8.10. For the latter two values there

is a slight degree of upward curvature, whereas for the value of F = .04 the plot is linear

with slope 12.2 psia

/cp/Mscf/d/hr, which implies that the pore volume drained is

35.5 × 10

cu ft. Using the values of h = 40 ft and

= .2 as average for the drainage

volume, the area is approximately 100 acres. Further, the intercept gives the value of

the Darcy flow coefficient B as 3186 psia

/cp/(Mscf/d).

It must be admitted that the stabilized analysis technique using the plot of equ. (8.47) is

a precarious business, to say the least. In this exercise any of the plots in fig. 8.10, for

different values of F, could be taken to be linear leading to estimates of the area of

60 acres, for F = .035, or 43 acres for F = .030. In a great many cases the high degree

of sensitivity to the value of F precludes any reliable estimate of the pore volume or

area drained being made.

To summarize the foregoing remarks on stabilized gas well testing; semi-steady flow

conditions will occur for some fixed value of

()

t 0.000264

φµ

= (8.36)

Therefore, such tests will be appropriate in reservoirs which have a high permeability

and small drainage area so that the semi-steady state condition will be reached in a

relatively short period of time. The reader should be cautioned, however, that these are

not the sole criteria. In exercise 8.1, for instance, the actual permeability is 100 mD and

the well is draining from the centre of a square of area 100 acres. Under these

circumstances the value of t

which must be exceeded before semi-steady state

conditions prevail is 0.1 (refer either MBH charts, fig. 7.11, or the Dietz chart fig.6.4).

REAL GAS FLOW: GAS WELL TESTING 270

Therefore, using equ. (8.36) and the data provided in exercise 8.1, the real time before

the semi-steady state condition is reached is

()

.1 c A

.1 .2 3.6 10 100 43560

t11.9hrs

0.000264k 0.000264 100

φµ

−

×× × × ×

== =

which confirms that, in this case, the separate twelve hour flow periods are just

sufficient to permit the test to be analysed using semi-steady state equations. Suppose,

however, the well was not situated at the centre of a square no-flow boundary but

instead, at the centre of one of the four quarters of the same square (graph III of

fig. 7.12(a)). In this case the value of t

before the semi-steady state condition is

reached is 0.5 and consequently, for the same reservoir properties, each flow period

would have to be about 60 hours before semi-steady state analysis could be correctly

applied. In this latter case, if the flow periods were each of twelve hour duration, the

application of the stabilized analysis technique would be inappropriate since the entire

test would be run under the late transient flow condition for which the m

functions

should be evaluated using equ. (8.40) rather than equ. (8.33). For high permeability

reservoirs, such as that tested in exercise 8.1, the error made in using the incorrect

mathematics in the analysis would not have too serious an effect on the values of

B and F determined from the test. For lower permeability reservoirs, however, use of

the incorrect mathematics could produce a more serious error.

One other disadvantage of the stabilized analysis techniques described so far is that

while they provide a value of the Darcy flow coefficient

1422T 4A

BlnS

kh C r

æö

ç÷

èø

there is no way of determining the individual components in this expression. In

exercise 8.1 these values happen to be k = 100 mD, A = 100 acres, C

= 30.9 and

S = 6.0 but, with the exception of A, which was obtained from the rather dubious

analysis in part four of the exercise, none of these can be explicitly calculated from the

test. This can have unfortunate consequences if the value of B, derived from the test, is

used in the inflow equation in an attempt to predict the long term deliverability of the

average reservoir well. For instance, the skin factor can be expected to be high in an

exploration well but this should be improved when drilling the average production well

using a more compatible completion fluid. Indeed, if the skin factor could be reduced to

zero in the well considered in exercise 8.1, the value of the flow coefficient B would be

reduced from 3176 to 1768 psia

/cp/(Mscf/d). Furthermore, if the reservoir is large and

requires more than one well for drainage the value of A and C

, which are implicit in the

value of B determined for the test well, will change during the producing lifetime of the

reservoir. Therefore, the use of the coefficient B in making long term predictions of well

deliverability can be misleading. It would be preferable if some analysis technique

could be employed which could explicitly determine k and S so that the coefficient B

could be calculated from its component parts, and such methods will now be described.

As deeper, less permeable gas reservoirs were discovered and tested it became

evident that the stabilized analysis techniques described so far in this section were