Dake L.P. Fundamentals of reservoir engineering

Подождите немного. Документ загружается.

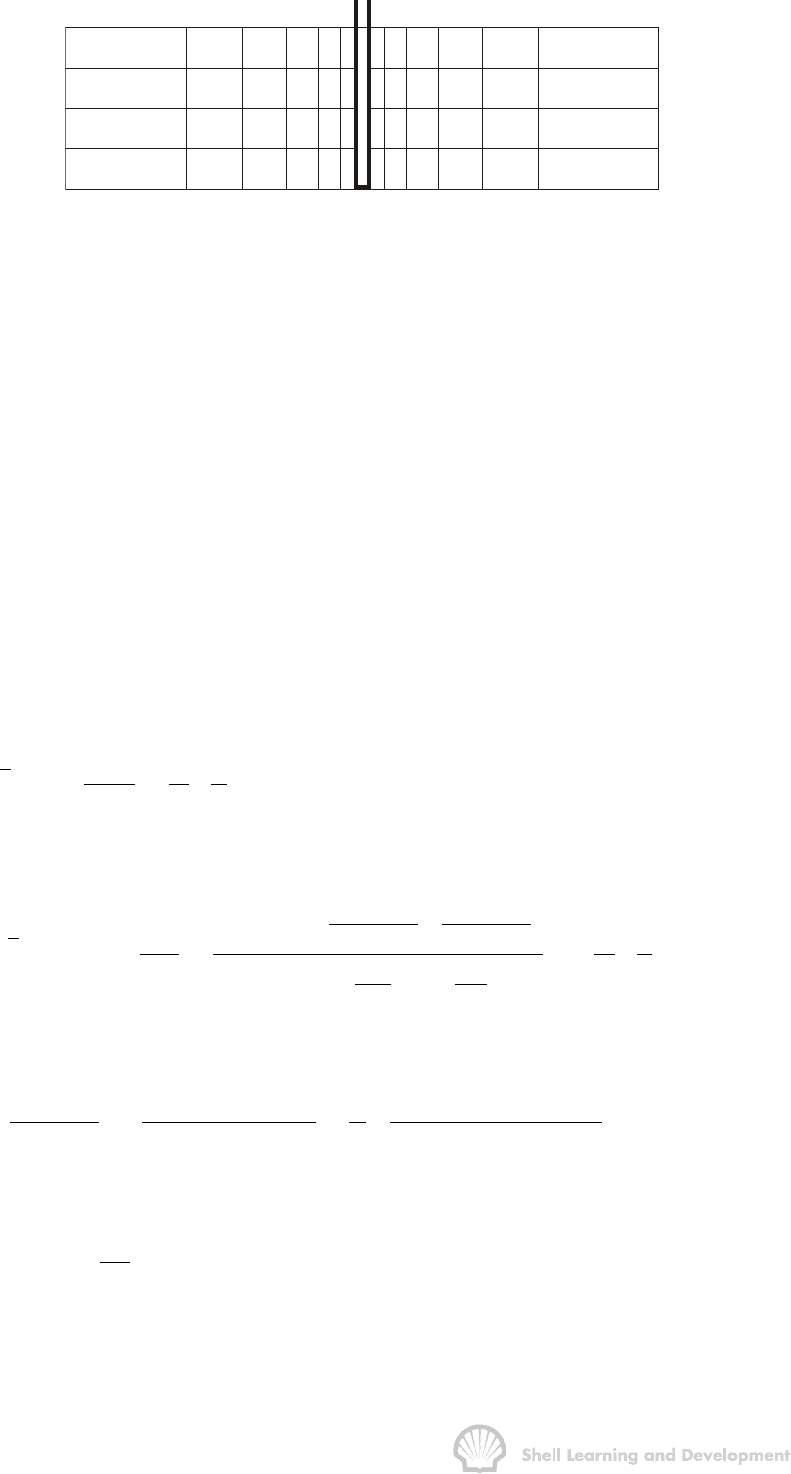
REAL GAS FLOW: GAS WELL TESTING 241

Fig. 8.1 Radial numerical simulation model for real gas inflow

The flow equations from block to block were solved numerically, using a finite

difference approximation, making due allowance for the variation of µ and Z as

functions of pressure. This is equivalent to solving the non-linear second order

differential equation (5.1). The results may be expected to be in slight error due to the

use of finite difference calculus, but the errors were minimized by making the grid

blocks smaller in the vicinity of the wellbore, where the pressure gradients are largest,

thus providing a higher resolution of solution in this region. With this model it was

hoped that some correcting factor could be found which could be used to match the

approximate analytical results, obtained by making the same assumptions as for a

single phase liquid, with the more exact results from the numerical simulation.

As an example of the approach taken by Russell and Goodrich, consideration will be

given to adapting the semi-steady state inflow equation, developed in chapter 6, sec. 2,

for the flow of oil, to an equivalent form which will be appropriate for the flow of gas.

The equation of interest, expressed in Darcy units, is

pp ln S

2kh r 4

æö

−= −+

ç÷

èø

(6.12)

which, when expressed in the field units specified in the previous section, becomes

()

s.cc / sec r.cc / sec

Q Mscf / d

atm 3

Mscf / d s.cc / sec

pp psi ln S

Dcm

psi r 4

2kmD hft

mD ft

éùéù

êúêú

æö

éù

ëûëû

−= −+

ç÷

êú

éù éù

ëû

èø

êú êú

ëû ëû

(8.1)

In this conversion the ratio

r.cc / sec reservoir cc / sec 1 1

s.cc / sec s tandard cc / sec E Gas expansion factor

éù

===

êú

ëû

and in field units



E35.37

(1.25)

and



p , the pressure at which E is evaluated, is as yet undefined. The full conversion of

the rate term in equation (8.1 ) can be expressed as

REAL GAS FLOW: GAS WELL TESTING 242

Mstb / d stb / d s.cc / sec 1

Q Mscf / d q r.cc / sec

Mscf / d Mstb / d stb / d E

éùéùé ù

êúêúê ú

ëûëûë û

[][]



1ZT

Q Mscf / d 1000 1.84 q r.cc / sec

5.615

35.37p

éù

×× =

êú

ëû



QZT

9.265 Mscf / d q r.cc / sec

Including the remaining conversion factors in equ. (8.1 ) yields



711 Q ZT 3

pp ln S

khp

æö

−= −+

ç÷

èø

(8.2)

Russell and Goodrich, comparing equ. (8.2) with the numerical simulation, found that

for the same reservoir and flow conditions the two were in close agreement providing

that the pressure



, at which the gas expansion factor was evaluated, was set equal to

the average of the current, average reservoir pressure and the bottom hole flowing

pressure i.e.



(8.3)

Furthermore, both µ and Z should also be evaluated at this same pressure so that

wf wf

pp pp

and Z Z

µµ

éù éù

êú êú

ëû ëû

(8.4)

and substituting these values of



p , µ and Z in equ. (8.2) gives

1422 Q ZT 3

pp ln S

kh r 4

æö

−= −+

ç÷

èø

(8.5)

Equ. (8.5) is the familiar p

formulation of the well inflow equation, under semi-steady

state conditions, which was tested by Russell and Goodrich and found to be applicable

over a wide range of reservoir conditions and flow rates.

Similarly, the transient line source solution for the same initial and boundary conditions

detailed in chapter 7, sec. 2, is

()

iwf

711 Q ZT 4 .000264kt

pp ln 2S

kh c r

γφµ

æö

−= +

ç÷

èø

(8.6)

wf wf

pp pp

and Z Z

µµ

éù éù

êú êú

ëû ëû

(8.4)

REAL GAS FLOW: GAS WELL TESTING 243

which is the real gas equivalent of equ. (7.10) in field units. This equation was also

found to compare favourably with the numerical simulation results, providing the

viscosity-compressibility product was evaluated as (µc)

, at the initial pressure p

(ref. sec. 8.8).

One obvious practical disadvantage in using the p

formulation can be appreciated by

considering a frequently occurring problem in gas inflow calculations, namely, the

calculation of p

if both p and Q are known using, in this case, the semi-steady state

inflow equation. A schematic of the calculation procedure is shown in fig. 8.2. If it is

assumed that

p has been determined in the drainage volume of the well from material

balance considerations then, for a fixed offtake rate, it will be necessary to solve the

inflow equation by iteration to determine p

since both µ and Z must be evaluated at

the pressure defined in equ. (8.4). In any iteration cycle

p is calculated using values

of µ

and Z

evaluated at the pressure

(p p ) / 2

−

+ , where k is the iteration counter. For

k = 1, both µ

and Z

can be evaluated at some convenient starting pressure, which in

this case has been selected as

p . When the difference between successive values of

p is less than some tolerance value (TOL) the iteration is terminated. Other

disadvantages in using the p

formulation for inflow equations will be discussed in

section 8.5.

8.4 THE AL-HUSSAINY, RAMEY, CRAWFORD SOLUTION TECHNIQUE

In their approach the authors attempted to linearize the basic flow equation, (5.1), using

the following version of the Kirchhoff integral transformation

()

pdp

mp 2

(8.7)

which was given the name, in this present context, of "the real gas pseudo pressure".

REAL GAS FLOW: GAS WELL TESTING 244

k = 1

= ( )

= Z( )p

k = 1

1422 Q Z T 3

plnS

kh r 4

ìü

æö

ïï

=− −+

íý

ç÷

ïï

èø

îþ

k = 1k +

k > 1

-1

éù

êú

ëû

-1

éù

êú

ëû

k = 1k +

accept p

-1

wf wf

TOL

−−

- from material balance

Fig. 8.2 Iterative calculation of p

using the p

formulation of the radial,

semi-steady state inflow equation, (8.5)

The limits of integration are between a base pressure p

and the pressure of interest p.

The value of the base pressure is arbitrary since in using the transformation only

differences in pseudo pressures are considered i.e.

()

bbwf

ppp

pdp pdp pdp

mp mp 2 2 2

ZZZ

µµµ

−= − =

òòò

As will be seen presently, it is possible, and indeed advantageous, to express all flow

equations in terms of these pseudo pressures rather than in the p

formulation of

Russell and Goodrich. However, conceptually it is more difficult and generally

engineers feel more comfortable dealing with p

rather than an integral transformation.

Therefore, it is worthwhile, at this stage, to examine the ease with which these

functions can be generated and used.

REAL GAS FLOW: GAS WELL TESTING 245

PVT data Numerical Integration Pseudo

pressures

p µ Z

p∆

×∆

m(p) p

=Σ ∆

(psia) (cp) (psia)

/cp

400 .01286 .937 66391 33196 400 13.278×10

13.278×10

800 .01390 .882 130508 98449 " 39.380 " 52.658 "

1200 .01530 .832 188537 159522 " 63.809 " 116.467 "

1600 .01680 .794 239894 214216 " 85.686 " 202.153 "

2000 .01840 .770 282326 261110 " 104.444 " 306.597 "

2400 .02010 .763 312983 297655 " 119.062 " 425.659 "

2800 .02170 .775 332986 322985 " 129.194 " 554.853 "

3200 .02340 .797 343167 338079 " 135.231 " 690.084 "

3600 .02500 .827 348247 345707 " 138.283 " 828.367 "

4000 .02660 .860 349711 348979 " 139.592 " 967.958 "

4400 .02831 .896 346924 348318 " 139.327 " 1107.285 "

TABLE 8.1

Generation of the real gas pseudo pressure, as a function of the actual pressure;

(Gas gravity, 0.85, temperature 200°F)

All the parameters in the integrand of equ. (8.7) are themselves functions of pressure

and can be obtained directly from PVT analysis of the gas at reservoir temperature or,

knowing only the gas gravity, from standard correlations of µ and Z, again at reservoir

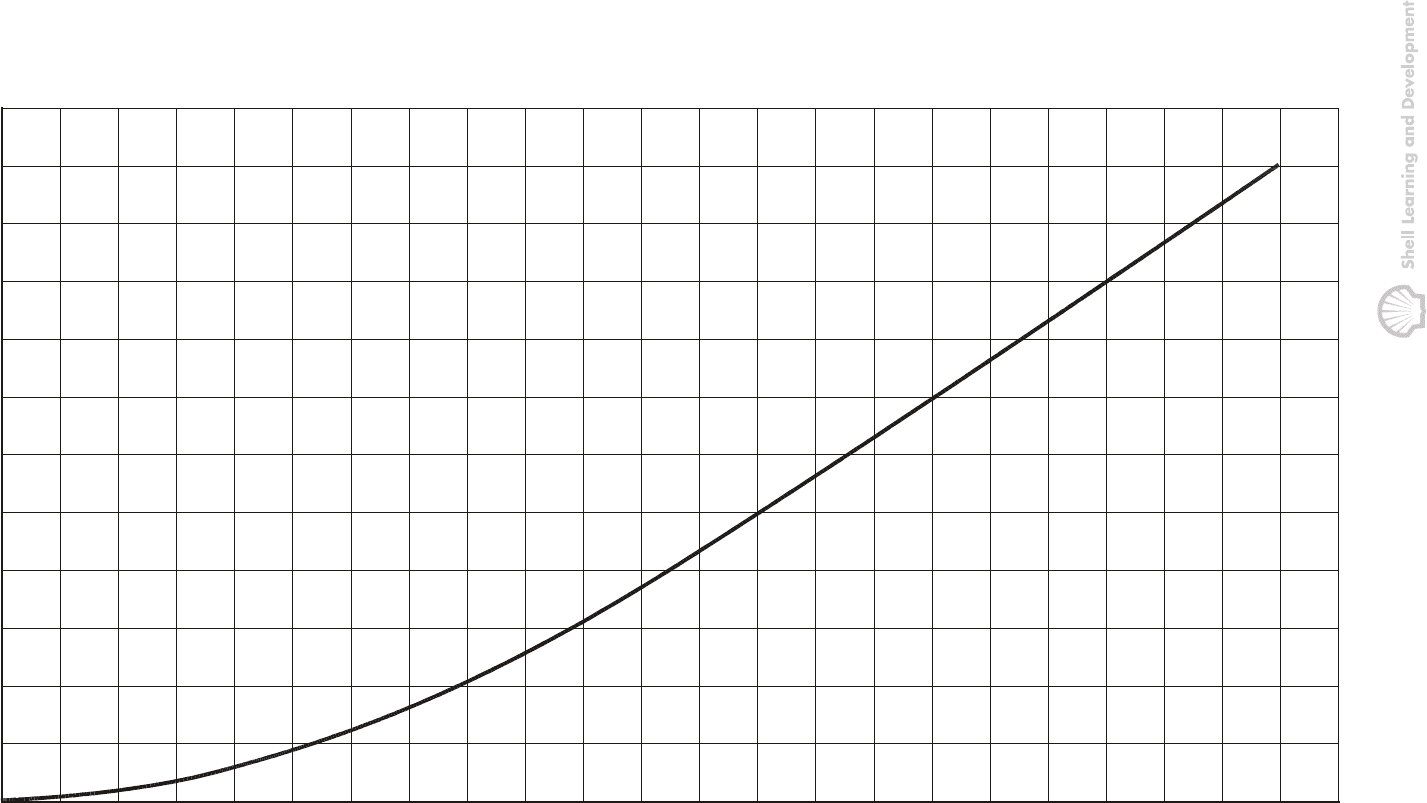
temperature. Table 8.1 lists a set of typical PVT data and shows how, using a simple

graphical method for numerical integration (trapezoidal rule), a table of values of m(p)

can be generated as a function of the actual pressures.

A graph of the values of m(p) versus pressure, corresponding to table 8.1, is included

as fig. 8.3. This plot is used in the gas well test exercises 8.1−3, (secs. 8.10−11), in

which it is assumed that for high pressures, in excess of 2800 psia, the function is

almost linear and can be described by

m (p) = (0.3457p - 414.76)× 10

psia

/cp

Having once obtained this relationship, the resulting plot should be preserved since it

will be relevant for the entire lifetime of the reservoir. Using the plot, it is always quite

straightforward to convert from real to pseudo pressures and vice versa.

REAL GAS FLOW: GAS WELL TESTING 246

In attempting to linearize the basic radial flow equation (5.1), (using, for the moment,

Darcy units), Al-Hussainy, Ramey and Crawford replaced the dependent variable p by

the real gas pseudo pressure m(p) in the following manner.

REAL GAS FLOW: GAS WELL TESTING 247

1200

800

600

400

200

1000

x10

m(p)

psia /cp

1000

2000

3000

4000 PRESSURE (psia)

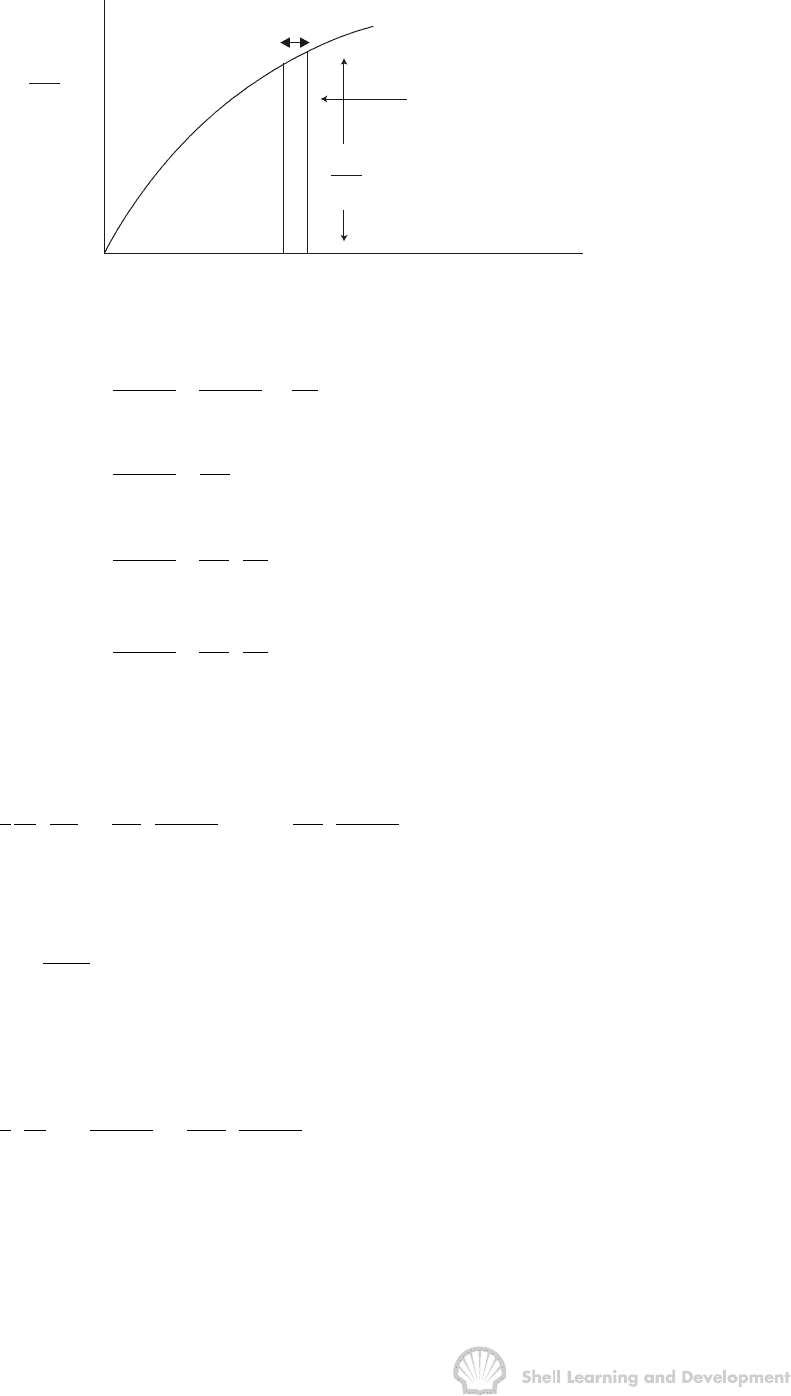
REAL GAS FLOW: GAS WELL TESTING 248

Fig. 8.3 Real gas pseudo pressure, as a function of the actual pressure, as derived in

table 8.1; (Gas gravity, 0.85; Temperature 200°F)

m (p)

∆∆

(Area) = m (p) = (2p / Z)

∆

Pressure

∆

Fig. 8.4 2p/µZ as a function of pressure

Since

() ()

mp mp

rpr

∂∂

∂

=⋅

∂∂∂

and

()

∂

∂Ζ

Then

()

2p p

∂

∂Ζ∂

(8.8)

and similarly

()

2p p

∂

∂Ζ∂

(8.9)

These relations are evident from fig. 8.4 and, substituting for ∂p/∂r and ∂p/∂t in

equ. (5.1), using equs. (8.8) and (8.9) gives

() ()

mp mp

rr 2p r 2p t

ρµ µ

φρ

æö

∂∂

∂Ζ Ζ

ç÷

∂∂ ∂

èø

(8.10)

Finally, using the equation of state for a real gas

ZRT

and substituting this expression for

in equ. (8.10) leads, after some cancellation of

terms, to the simplified expression

() ()

mp mp

rr r k t

φµ

æö

∂∂

∂

ç÷

∂∂ ∂

èø

(8.11)

Equation (8.11) has precisely the same form as the diffusivity equation, (5.20), except

that the dependent variable has been replaced by m(p).

REAL GAS FLOW: GAS WELL TESTING 249

Note that in reaching this stage it has not been necessary to make any restrictive

assumptions about the viscosity being independent of pressure or that the pressure

gradients are small and hence squared pressure gradient terms are negligible, as was

implicit in the approach of Russell and Goodrich.

Therefore, the problem has already been partially solved but it should be noted that the

term

φµ

c/k in equ. (8.11) is not a constant, as it was in the case of liquid flow, since for

a real gas both

and c are highly pressure dependent. Equation (8.11) is therefore, a

non-linear form of the diffusivity equation.

Continuing with the argument; in order to derive an inflow equation under semi-steady

state flow conditions, then applying the simple material balance for a well draining a

bounded part of the reservoir at a constant rate

cV q

∂∂

=− =−

∂∂

(5.8)

and for the drainage of a radial volume element

rh c

∂

=−

∂

(5.10)

Also, using equ. (8.9)

()

2p p 2p q

rh c

µµ

∂

=⋅=−⋅

∂Ζ∂Ζ

(8.12)

and substituting equ. (8.12) in (8.11) gives

()

1c2pq

rr r k rhc

φµ

µπ

æö

∂

=− ⋅ ⋅

ç÷

∂∂ Ζ

èø

()

eres

12pq

rr r rkh

æö

∂

æö

=−

ç÷

∂∂ Ζ

èø

(8.13)

Furthermore, using the real gas equation of state,

sc sc

res

pq T

æö

ç÷

èø

equ. (8.13) can be expressed as

()

sc sc

sce

2p q

rr r Trkh

æö

∂

=− ⋅

ç÷

∂∂

èø

(8.14)

REAL GAS FLOW: GAS WELL TESTING 250

- from material balance

m (p)

m ( )p

p p

m (p)

m (p )

m (p ) = m ( )

m ( )p

1422 QT 3

ln S

kh r 4

−−+

ç÷

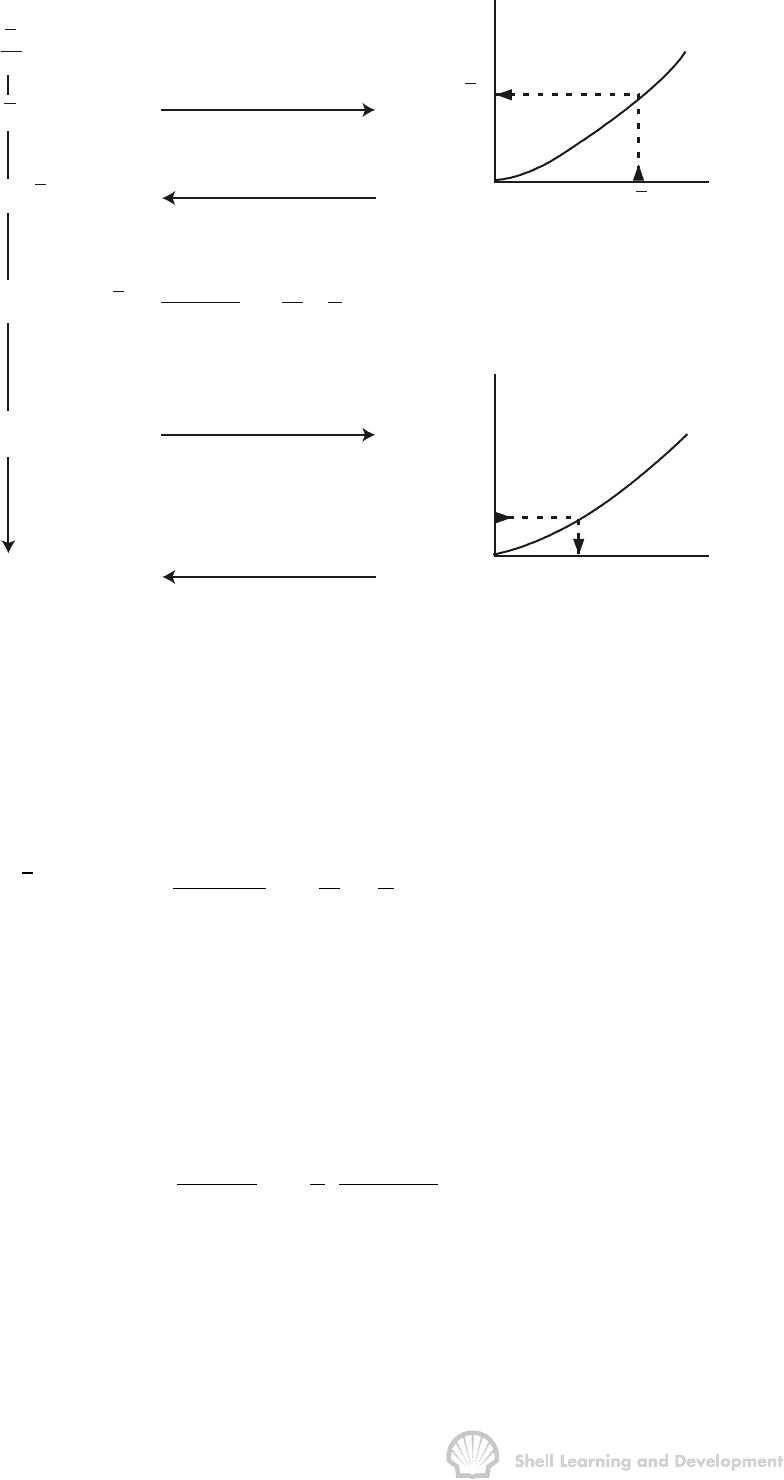
Fig. 8.5 Calculation of p

using the radial semi-steady state inflow equation

expressed in terms of real gas pseudo pressures, (equ. 8.15)

For isothermal reservoir depletion, the right hand side of equ. (8.14) is a constant, and

the differential equation has been linearized. A solution can now be obtained using

precisely the same technique as applied in Chapter 6, sec. 2, for liquid flow. If, in

addition, field units are employed then the resulting semi-steady state inflow equation

can be expressed as

()

1422 QT 3

mp mp ln S

kh r 4

æö

−= −+

ç÷

èø

(8.15)

Note that this equation has a similar form to the p

formulation of equ. (8.5), except that

the right hand side no longer contains the pressure dependent

Z term which is now

implicit in the pseudo pressures. Because of this, the practical difficulty in having to

iterate when solving the inflow equation for p

is removed. The relevant steps

corresponding to fig. 8.2 are shown in fig. 8.5. Similarly, the transient line source

solution, when expressed in pseudo pressures and field units, becomes

() ( )

()

iwf

711 QT 4 .000264kt

mp mp ln 2S

kh c r

γφµ

æö

−= +

ç÷

èø

(8.16)