Cohen I.M., Kundu P.K. Fluid Mechanics
Подождите немного. Документ загружается.


792 Introduction to Biofluid Mechanics
representative of all of the peripheral vessels. The rigid tube offers constant resistance,
R, equal to the total peripheral resistance that was evaluated in the Hagen-Poiseuille
model, equation (17.9). From the law of conservation of mass, assuming blood is
incompressible,
Rate of Inflow into Aorta = Rate of change of volume of elastic chamber
+ Rate of outflow into rigid tube. (17.47)
Let the instantaneous blood pressure in the elastic chamber be p(t), and its volume be
v(t). The pressure on the outside of the aorta is taken to be zero. The rate of change
of volume of an elastic chamber is given by,
dv
dt
=
dv
dp
dp
dt
. (17.48)
In equation (17.48), the quantity
dv
dp
is the compliance, K, of the vessel and is a
measure of the distensibility. Compliance at a given pressure is the rate of change in
volume with respect to a change in pressure. Here pressures are always understood
to be transmural pressure differences. Compliance essentially represents the disten-
sibility of the vascular walls in response to a certain pressure. Also, from equation
(17.9), rate of flow into peripherals is given by
(
p(t)/R
)
, where we have assumed
¯p
V
= 0. Therefore, equation (17.47) becomes,
Q(t) = K
dp
dt
+
p(t)
R
. (17.49)
The equation (17.49) is a linear equation of the form,
Q =
dy
dx
+ Py, (17.50)
whose solution is,
ye
Pdx
= A +
Qe
Pdx
dx. (17.51)
From equations (17.49) and (17.51), with p
0
denoting p at t = 0, the instantaneous
pressure p in the aorta as a function of the left ventricular ejection rate Q(t) is
given by,
p(t) =
1
K
e
−t/RK
t
0
Q(τ )e
τ/RK
dτ + p
0
e
−t/RK
. (17.52)
In equation (17.52), p
0
would be the aortic pressure at the end of diastolic phase.
A fundamental assumption in the Windkessel theory is that the pressure pulse
wave generated by the heart is transmitted instantaneously throughout the arterial
system and disappears before the next cardiac cycle. In reality, pressure waves require
finite but small transmission times, and are modified by reflection at bifurcations,
bends, tapers, and at the end of short tubes of finite length, and so on. We will now
account for some of these features.

3. Modelling of Flow in Blood Vessels 793
Pulse Wave Propagation in an Elastic Tube: Inviscid Theory
Consider a homogeneous, incompressible, and inviscid fluid in an infinitely long,
horizontal, cylindrical, thin walled, elastic tube. Let the fluid be initially at rest. The
propagation of a disturbance wave of small amplitude and long wave length compared
to the tube radius is of interest to us. In particular, we wish to calculate the wave speed.
Since the disturbance wave length is much greater than the tube diameter, the time
dependent internal pressure can be taken to be a function only of (x, t).
Before we embark on developing the solution, we need to understand the inviscid
approximation. For flow in large arteries, the Reynolds and Womersley numbers are
large, the wall boundary layers are very thin compared to the radius of the vessel.
The inviscid approximation may be useful in giving us insights in understanding
such flows. Clearly, this will not be the case with arterioles, venules and capillaries.
However, the inviscid analysis is strictly of limited use since it is the viscous stress
that is dominant in determining flow stability in large arteries.
Under the various conditions prescribed, the resulting flow may be treated as one
dimensional.
Let A(x, t ) and u(x, t) denote the the cross sectional area of the tube and the
longitudinal velocity component, respectively. The continuity equation is:
∂A
∂t
+
∂(Au)
∂x
= 0, (17.53)
and, the equation for the conservation of momentum is:
ρA
∂u
∂t
+ u
∂u
∂x
=−
∂
((
p − p
e
)
A
)
∂x
, (17.54)
where
(
p − p
e
)
is the transmural pressure difference. Since the tube wall is assumed
to be elastic (not viscoelastic), under the further assumption that A depends on the
transmural pressure difference (p − p
e
) alone, and the material obeys Hooke’s law,
we have from equation (17.41), the pressure—radius relationship (referred to as
“tube law”),
p − p
e
=
Eh
a
0
1 −
a
0
a
=
Eh
a
0
1 −
A
0
A
1
2
, (17.55)
where A = πa
2
, and A
0
= πa
2
0
. The equations (17.53), (17.54), and (17.55) govern
the wave propagation. We may simplify this equation system further by linearizing
it. This is possible if the pressure amplitude (p − p
e
) compared to p
0
, the induced
fluid speed u, and (A − A
0
) compared to A
0
, and their derivatives are all small.
If the pulse is moving slowly relative to the speed of sound in the fluid, the wave
amplitude is much smaller than the wave length, and the distension at one cross
section has no effect on the distension elsewhere, the assumptions are reasonable.
As discussed by Pedley (2000), in normal human beings, the mean blood pressure,
relative to atmospheric, at the level of the heart is about 100 mmHg, and there is a
cyclical variation between 80 and 120 mmHg, so the amplitude-to-mean ratio is 0.2,

794 Introduction to Biofluid Mechanics
which is reasonably small. Also, in the ascending aorta, the pulse wave speed, c,is
about 5 m/s, and the maximum value of u is about 1 m/s, and (u/c) is also around
0.2. In that case, the system of equations reduce to
∂A
∂t
+ A
0
∂u
∂x
= 0, (17.56)
and,
ρ
∂u
∂t
=−
∂p
∂x
, (17.57)
and,
p − p
e
=
Eh
2a
0
A
0
(
A − A
0
)
, and
∂p
∂A
=
Eh
2a
0
A
0
(17.58)
Differentiating equation (17.56) with respect to t and equation (17.57) with respect
to x, and subtracting the resulting equations, we get,
∂
2
A
∂t
2
=
A
0
ρ
∂
2
p
∂x
2
, (17.59)
and with equation (17.58), we obtain,
∂
2
p
∂t
2
=
Eh
2a
0
A
0
∂
2
A
∂t
2
=
∂p
∂A
A
0
ρ
∂
2
p
∂x
2
. (17.60)
Combining equations (17.59) and (17.60), we produce,
∂
2
p
∂x
2
=
1
c
2
∂
2
p
∂t
2
, or,
∂
2
p
∂t
2
= c
2
(A
0
)
∂
2
p
∂x
2
, (17.61)
where, c
2
=
Eh
2ρa
0
=
A
ρ
dp
dA
. Equation (17.61) is the wave equation, and the quantity,
c =
Eh
2ρa
0
=
A
ρ
dp
dA
, (17.62)
is the speed of propagation of the pressure pulse. This is known as the
Moens-Korteweg wave speed. If the thin wall assumption is not made, following Fung
(1997), by evaluating the strain on the midwall of the tube,
c =
Eh
2ρ
(
a
0
+ h/2
)
, (17.63)
Next, similar to equation (17.61), we can develop,
∂
2
u
∂x
2
=
1
c
2
∂
2
u
∂t
2
, (17.64)

3. Modelling of Flow in Blood Vessels 795
for the velocity component u. The wave equation (17.61) has the general solution,
p = f
1
t −
x
c
+ f
2
t +
x
c
, (17.65)
where f
1
and f
2
are arbitrary functions; f
2
is zero if the wave propagates only in
the +x direction. This result states that the small amplitude disturbance can propagate
along the tube, in either direction, without change of shape of the wave form, at speed
c(a
0
). Also, the velocity wave form is predicted to be of the same shape as the pressure
wave form.
In principle, the Moens-Korteweg wave speed given in equation (17.63) must
enable the determination of the arterial modulus E as a function of a by noninvasive
measurement of the values of arterial dimensions (a, h), the wave forms of the arterial
inner radius at two sites, the transit time (as the time interval between the wave form
peaks), and hence the pulse wave velocity. More details in this regard are available in
the book by Mazumdar (1999).
Next, consider the solutions of wave equations (17.61) and (17.64),
p =ˆp
1
f(x − ct) +ˆp
2
g(x + ct), (17.66)
and,
u =ˆu
1
f(x − ct) +ˆu
2
g(x + ct), (17.67)
where ˆp
1
, ˆu
1
, ˆp
2
, and, ˆu
2
, are the pressure and velocity amplitudes for waves
travelling in the positive x-direction and negative x-direction, respectively. From
equation (17.57),
ˆp
1
= ρcˆu
1
, and, ˆp
2
=−ρcˆu
2
. (17.68)
This equation (17.68) relates the amplitudes of the pressure and velocity waves.
The above analysis would equally apply if the inviscid fluid in the tube was
initially in steady motion, say from left to right. In that case, u would have to be
regarded as a small perturbation superposed on the steady flow, and c would be the
speed of the perturbation wave relative to the undisturbed flow.
Let us now examine the limitations of the above model. For typical flow in the
aorta, the speed of propagation of the pulse is about 4 m/s (Brown et al. (1999)),
about 5 m/s in the ascending aorta, rising to about 8 m/s in more peripheral arteries.
These predictions are very close to measured values in normal subjects, either dogs
or humans (Pedley (2000)). The peak flow speed is about 1 m/s. The speed of propa-
gation in a collapsible vein might be as low as 1 m/s, and this may lead to phenomena
analogous to sonic flow (Brown et al. (1999)). From equation (17.62), for given E,
h, ρ, and size of vessel, the wave speed is a constant. Experimental studies indicate,
however, that the wave speed is a function of frequency. The shape of the wave form
does not remain the same. The theory must be modified to account for peaking of
the pressure pulse due to wave reflection from arterial junctions, wave front steep-
ening due to nonlinear dispersion effects ( Lighthill (1978)), and observed velocity
wave form by including dissipative effects due to viscosity (Lighthill (1975), Pedley
(2000)). The neglect of the inertial terms and the effects of viscosity have therefore

796 Introduction to Biofluid Mechanics
to be examined to address these concerns and to develop a systematic understanding.
These issues will be addressed in later sections in the following order. First, we will
learn about pulsatile viscous flow in a rigid walled single straight tube. This would
imply the assumption of an infinite wave speed. Subsequent to that, we will examine
the effects of wall elasticity on pulsatile viscous flow in a single tube to gain a more
realistic understanding. This would allow us to understand wave transmission at finite
speed. Following this, we will study blood vessel bifurcation. This will be extended
to understand the effects of wave reflection from arterial junctions under the inviscid
flow approximation.
Pulsatile Flow in a Rigid Cylindrical Tube: Viscous Effects Included, Infinite
Wave Speed Assumption
Consider the axi-symmetric flow of a Newtonian incompressible fluid in a long, thin,
circular, cylindrical, horizontal, rigid walled tube. Clearly, the assumption of a rigid
wall implies that the speed of wave propagation is infinite and unrealistic. However,
the development presented here will provide us with useful insights and these will be
helpful in formulating a much improved theory in the next section.
We shall employ the cylindrical coordinates (r,θ,x) with velocity components
(u
r
,u
θ
, and,u
x
), respectively. Let λ be the wave length of the pulse. This is long, and
a λ. Since the wave speed is infinite, all the velocity components are very much
smaller than the wave speed. These assumptions would enable us to drop the inertial
terms in the momentum equations. With the additional assumptions of axi-symmetry
(u
θ
= 0, and
∂
∂θ
= 0), and rigid tube wall, (u
r
= 0), and omitting the subscript x in
u
x
for convenience, the continuity equation may be written:
∂u
∂x
= 0, (17.69)
and the r-momentum equation is:
0 =−
∂p
∂r
(17.70)
and the x momentum equation is:
ρ
∂u
∂t
=−
∂p
∂x
+ µ
∂
2
u
∂r
2
+
1
r
∂u
∂r
(17.71)
We see that u = u(r, t) and p = p(x, t). Therefore, we are left with just one equation:
µ
∂
2
u
∂r
2
+
1
r
∂u
∂r
− ρ
∂u
∂t
=
∂p
∂x
. (17.72)
In equation (17.72), since p = p(x, t),
∂p
∂x
will be a function only of t . Since the
pressure wave form is periodic, it is convenient to express the partial derivative of
pressure using a Fourier series. Such a periodic function depends on the fundamental

3. Modelling of Flow in Blood Vessels 797
frequency of the signal, ω, heart rate (unit, rad/s), and the time t. Recall that ω is also
called the circular frequency, ω/2π is the frequency (unit, Hz), and λ is the wave
length, (unit, m). Also, λ = c/(ω/2π), where c is wave speed. The wave length is
the wave speed divided by frequency, or the distance travelled per cycle.
We set
∂p
∂x
=−Ge
iωt
, (17.73)
where G is a constant denoting the amplitude of the pressure gradient pulse and
e
iωt
= cos ωt +i sin ωt. With this representation for p(t), equation (17.72) becomes:
µ
∂
2
u
∂r
2
+
1
r
∂u
∂r
− ρ
∂u
∂t
=
∂p
∂x
=−Ge
iωt
(17.74)
This is a linear, second order, partial differential equation with a forcing function.
For ω = 0, the flow is described by the Hagen-Poiseuille model. Womersley (1955a,
1955b), has solved this problem, and we will provide essential details.
For ω = 0, we may try solutions of the form,
u(r, t) = U(r)e
iωt
, (17.75)
where, U(r) is the velocity profile in any cross section of the tube. The real part
in equation (17.75) gives the velocity for the pressure gradient G cos ωt and the
imaginary part gives the velocity for the pressure gradient G sin ωt. Assume that the
flow is identical at each cross section along the tube. From equations (17.74) and
(17.75), we get:
d
2
U
dr
2
+
1
r
dU
dr
−
iωρ
µ
U =
G
µ
. (17.76)
This is a Bessel’s differential equation, and the solution would involve Bessel func-
tions of zeroth order and complex arguments. Thus,
U(r) = C
1
J
0
i
(
iωρ/µ
)
r
+ C
2
Y
0
i
(
iωρ/µ
)
r
+
G
ωρ i
, (17.77)
where C
1
and C
2
are constants. In equation (17.77), from the requirement that U is
finite at r = 0, C
2
= 0. For a rigid walled tube, U = 0atr = a. Therefore,
C
1
J
0
i
3/2
(
ωρ /µ
)
a
+
G
ωρ i
= 0. (17.78)
From equation (17.12), the Womersley number is defined by α = a
√
ω/ν. Therefore,
from equation (17.78), we may write,
C
1
=
iG
ωρ
1
J
0
i
3/2
α
. (17.79)
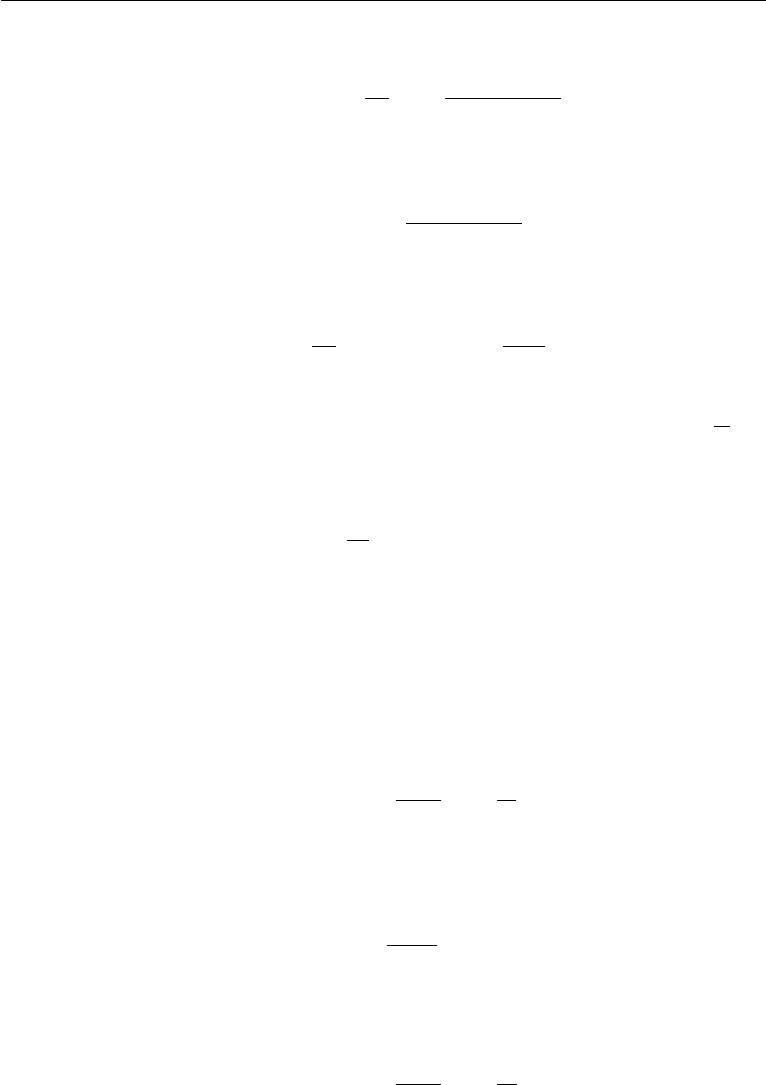
798 Introduction to Biofluid Mechanics
Therefore, from equation (17.77),
U(r) =−
iG
ωρ
1 −
J
0
i
3/2
αr/a
J
0
i
3/2
α
. (17.80)
Introduce, for convenience,
F
1
(α) =
J
0
i
3/2
αr/a
J
0
i
3/2
α
. (17.81)
Now, from equation (17.75),
u(r, t) = U(r)e
iωt
=−
iG
ωρ
(
1 − F
1
(α)
)
e
iωt
=
Ga
2
iµα
2
(
1 − F
1
(α)
)
e
iωt
. (17.82)
In the above development, we have found the velocity as a function of radius r and
time t for the entire driving pressure gradient. Since we have represented both
∂p
∂x
and
u(r, t) in terms of Fourier modes, we could also express the solution for both these
quantities in terms of individual Fourier modes or harmonics explicitly as,
∂p
∂x
=−
N
n=0
G
n
e
inωt
, (17.83)
where N is the number of modes (harmonics), and the n = 0 term represents the
mean pressure gradient. Similarly, for velocity,
u(r, t) = u
0
(r) +
N
1
u
n
(r)e
inωt
(17.84)
In equation (17.84),
u
0
(r) =
G
0
a
2
4µ
1 −
r
2
a
2
, (17.85)
is the mean flow and is recognized as the steady Hagen-Poiseuille flow with G
0
as
the mean pressure gradient, and, for each harmonic,
u
n
(r) =
G
n
a
2
iµα
n
2
(
1 − F
1
(α
n
)
)
(17.86)
We can now write down the expressions for u
n
(r) in the limits of α
n
small and large.
These are, for α
n
small,
u
n
(r) ≈
G
n
a
2
4µ
1 −
r
2
a
2
, (17.87)

3. Modelling of Flow in Blood Vessels 799
which represents a quasi-steady flow, and for α
n
large,
u
n
(r) ≈
G
n
a
2
iµα
n
2
1 − exp
−
ω
2ν
(1 + i)(a − r)
, (17.88)
which is the velocity boundary layer on a plane wall in an oscillating flow. This flow
was discussed in Chapter 9 (Stokes second problem).
The volume flow rate, Q(t), may be obtained by integrating the velocity profile
across the cross section. Thus, from equations (17.85) and (17.86)
Q(t) =
a
0
u 2 πrdr = πa
2
G
0
a
2
8µ
+
a
2
iµ
∞
1
G
n
α
n
2
[
1 − F
2
(α
n
)
]
e
inωt
,
(17.89)
or equivalently, with equation (17.82),
Q(t) =
a
0
2πe
iωt
Ga
2
iµα
2
(
1 − F
1
(α)
)
rdr =
πa
4
iµα
2
G
(
1 − F
2
(α)
)
e
iωt
, (17.90)
where,
F
2
(α) =
2J
1
i
3/2
α
i
3/2
αJ
0
i
3/2
α
. (17.91)
The real part of equation (17.90) gives the volume flow rate when the pressure gradient
is G cos ωt and the imaginary part gives the rate when the pressure gradient is G sin ωt.
Next, the wall shear rate, τ(t)|
r=a
is given by,
τ(t)|
r=a
=
∂u
∂r
r=a
=
G
0
a
2
+
a
2
N
1
G
n
F(α
n
)e
inωt
(17.92)
We may now examine the flow rates in the limit cases of α → 0 and α →∞.As
α → 0, by Taylor’s expansion,
F
2
(α) ≈ 1 −
iα
2
8
− O(α
4
), (17.93)
and, from equation (17.90), in the limit as α → 0,
Q =
πGa
4
8µ
e
inωt
, (17.94)
and the magnitude of the volumetric flow rate, Q
0
, in the limit as α → 0 is,
|Q
0
|=
πGa
4
8µ
, (17.95)
as would be expected (Hagen-Poiseuille result). As α →∞,
F
2
(α) ≈
2
i
1/2
α
1 +
1
2α
, (17.96)

800 Introduction to Biofluid Mechanics
Next, in Hagen-Poiseuille flow, the steady flow rate is the maximum attainable
and there is no phase lag between the applied pressure gradient and the flow. To
understand the phase difference between the applied pressure gradient pulse and the
flow rate in the present flow model, we set,
(1 − F
2
(α)) = Z(α), Z(α) = X(α) + iY (α) (17.97)
Then from equation (17.90),
Q =
πGa
4
µα
2
{
[
Y cos(ωt) + X sin(ωt )
]
− i
[
X cos(ωt) − Y sin(ωt)
]
}
(17.98)
The magnitude of Q is,
|Q|=
πGa
4
µα
2
X
2
+ Y
2
. (17.99)
The phase angle between the applied pressure gradient Ge
iωt
and the flow rate (equa-
tion (17.90)) is now noted to be,
tan φ =
X
Y
. (17.100)
With increasing ω, the phase lag between the pressure gradient and the flow rate
increases, and the flow rate decreases. Thus, the magnitude of the volumetric flow
rate, |Q|, given by equation (17.99) will be considerably less than the magnitude |Q
0
|
given by equation (17.95) as would be expected. For an arterial flow, with α = 8,
X ≈ 0.85, Y ≈ 0.16, the pulsed volumetric flow rate, |Q| would be just about one
tenth of the steady value, |Q
0
|. For more detailed discussions and comparisons with
measured values of pressure gradients and flow rates in blood vessels, see Nichols
and O’Rourke (1998).
The above analysis assumed an infinite wave speed of propagation. In order to
accommodate the requirement of wave transmission at a finite wave speed, we need
to account for vessel wall elasticity. This will be discussed in the next section.
Wave Propagation in a Viscous Liquid Contained in an Elastic Cylindrical Tube
Blood vessel walls are viscoelastic. But in large arteries the effect of nonlinear
viscoelasticity on wave propagation is not so severe (Fung, 1997). Even where vis-
coelastic effects are important, an understanding based on elastic walls will be useful.
In this section, we will first study the effects of elastic walls. Then, we will briefly
discuss the effects of wall viscoelasticity.
Consider a long, thin, circular, cylindrical, horizontal elastic tube containing
a Newtonian, incompressible fluid. Let this system be set in motion solely due to a
pressure wave, and the amplitude of the disturbance be small enough so that quadratic
terms in the amplitude are negligible compared with linear ones.
In the formulation, we have to consider the fluid flow equations together with the
equations of motion governing tube wall displacements. Assume that the tube wall
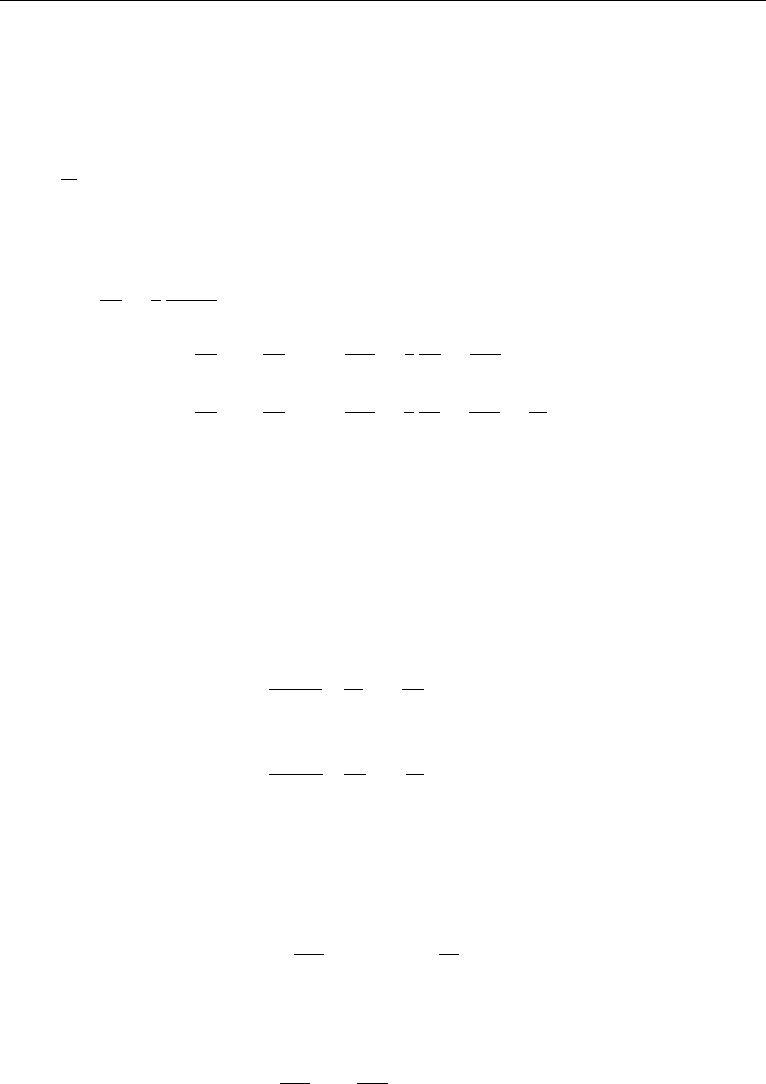
3. Modelling of Flow in Blood Vessels 801
material obeys Hooke’s law. Since the tube is thin, membrane theory for modelling
the wall displacements is adequately accurate, and we will neglect bending stresses.
The primary question is, how does viscosity attenuate velocity and pressure in
this flow?
We shall employ the cylindrical coordinates (r,θ,x) with velocity compo-
nents (u
r
,u
θ
, and,u
x
), respectively. With the assumption of axi-symmetry, u
θ
=
0 and
∂
∂θ
= 0. For convenience, we write the u
r
component as v, and we omit the
subscript x in u
x
.
Restricting the analysis to small disturbances, the governing equations for the
fluid are:
∂u
∂x
+
1
r
∂(rv)
∂r
= 0, (17.101)
ρ
∂u
∂t
=−
∂p
∂x
+ µ
∂
2
u
∂r
2
+
1
r
∂u
∂r
+
∂
2
u
∂x
2
, (17.102)
ρ
∂v
∂t
=−
∂p
∂r
+ µ
∂
2
v
∂r
2
+
1
r
∂v
∂r
+
∂
2
v
∂x
2
−
v
r
2
, (17.103)
where u and v are the velocity components in the axial and radial directions, respec-
tively.
These have to be supplemented with the tube wall displacement equations. Let
the tube wall displacements in the (r,θ,x) directions be (η, ζ, and ξ ), respectively,
and the tube material density be ρ
w
. The initial radius of the tube is a
0
, and the wall
thickness is h.
For this thin elastic tube, the circumferential (hoop) tension and the tension in
the axial direction are related by Hooke’s law as follows:
T
θ
=
Eh
1 −ˆν
2
η
a
0
+ˆν
∂ξ
∂x
, (17.104)
and
T
x
=
Eh
1 −ˆν
2
∂ξ
∂x
+ˆν
η
a
0
, (17.105)
where ˆν is Poisson’s ratio.
By a force balance on a wall element of volume (h rdθ dx), the equations
governing wall displacements may be written as:
• r-direction
ρ
w
h
∂
2
η
∂t
2
= σ
rr
|
r=a
−
T
θ
a
0
, (17.106)
and
• x-direction
ρ
w
h
∂
2
ξ
∂t
2
=+
∂T
x
∂x
− σ
rx
|
r=a
. (17.107)
