Cohen I.M., Kundu P.K. Fluid Mechanics

Подождите немного. Документ загружается.

182 Irrotational Flow

At the surface of the cylinder, velocity is entirely tangential and is given by

r =a

=−2 U sin θ −



2πa

, (6.39)

which vanishes if

sin θ =−



4πaU

. (6.40)

For <4πaU, two values of θ satisfy equation (6.40), implying that there are two

stagnation points on the surface. The stagnation points progressively move down as

 increases (Figure 6.14) and coalesce at  = 4πaU.For>4πaU, the stagnation

point moves out into the ﬂow along the y-axis. The radial distance of the stagnation

point in this case is found from

θ=−π/2

= U



1 +



−



2πr

= 0.

This gives

r =

4πU

[ ±





− (4πaU)

one root of which is r>a; the other root corresponds to a stagnation point inside the

cylinder.

Pressure is found from the Bernoulli equation

p + ρq

/2 = p

∞

+ ρU

/2.

Using equation (6.39), the surface pressure is found to be

r =a

= p

∞



−



−2U sin θ −



2πa





. (6.41)

The symmetry of ﬂow about the y-axis implies that the pressure force on the cylinder

has no component along the x-axis. The pressure force along the y-axis, called the

“lift” force in aerodynamics, is (Figure 6.15)

L =−



2π

r =a

sin θadθ.

Substituting equation (6.41), and carrying out the integral, we ﬁnally obtain

L = ρU, (6.42)

where we have used



2π

sin θdθ =



2π

sin

θdθ= 0.

10. Flow past a Circular Cylinder with Circulation 183

Figure 6.15 Calculation of pressure force on a circular cylinder.

It is shown in the following section that equation (6.42) holds for irrotational ﬂows

around any two-dimensional shape, not just circular cylinders. The result that lift force

is proportional to circulation is of fundamental importance in aerodynamics. Relation

equation (6.42) was proved independently by the German mathematician, Wilhelm

Kutta(1902),andthe Russian aerodynamist,NikolaiZhukhovsky(1906);itis called the

Kutta–Zhukhovskylift theorem. (Older western textstransliterated Zhukhovsky’s name

as Joukowsky.) The interesting question of how certain two-dimensional shapes, such

as an airfoil, develop circulation when placed in a stream is discussed in chapter 15. It

will be shownthere that ﬂuidviscosity isresponsible forthe developmentofcirculation.

Themagnitude of circulation,however, isindependentof viscosity, anddependson ﬂow

speed U and the shape and “attitude” of the body.

For a circular cylinder, however, the only way to develop circulation is by rotating

it in a ﬂow stream. Although viscous effects are important in this case, the observed

pattern for large values of cylinder rotation displays a striking similarity to the ideal

ﬂow pattern for >4πaU; see Figure 3.25 in the book by Prandtl (1952). For

lower rates of cylinder rotation, the retarded ﬂow in the boundary layer is not able

to overcome the adverse pressure gradient behind the cylinder, leading to separation;

the real ﬂow is therefore rather unlike the irrotational pattern. However, even in the

presence of separation, observed speeds are higher on the upper surface of the cylinder,

implying a lift force.

A second reason for generating lift on a rotating cylinder is the asymmetry gen-

erated due to delay of separation on the upper surface of the cylinder. The resulting

asymmetry generates a lift force. The contribution of this mechanism is small for

two-dimensional objects such as the circular cylinder, but it is the only mechanism

for side forces experienced by spinning three-dimensional objects such as soccer,

tennis and golf balls. The interesting question of why spinning balls follow curved

paths is discussed in Chapter 10, Section 9. The lateral force experienced by rotating

bodies is called the Magnus effect.

The nonuniqueness of solution for two-dimensional potential ﬂows should be

noted in the example we have considered in this section. It is apparent that solutions

for various values of  all satisfy the same boundary condition on the solid surface

184 Irrotational Flow

(namely, no normal ﬂow) and at inﬁnity (namely, u = U ), and there is no way to

determine the solution simply from the boundary conditions. A general result is that

solutions of the Laplace equation in a multiply connected region are nonunique. This

is explained further in Section 15.

11. Forces on a Two-Dimensional Body

In the preceding section we demonstrated that the drag on a circular cylinder is zero

and the lift equals L = ρU. We shall now demonstrate that these results are valid

for cylindrical shapes of arbitrary cross section. (The word “cylinder” refers to any

plane two-dimensional body, not just to those with circular cross sections.)

Blasius Theorem

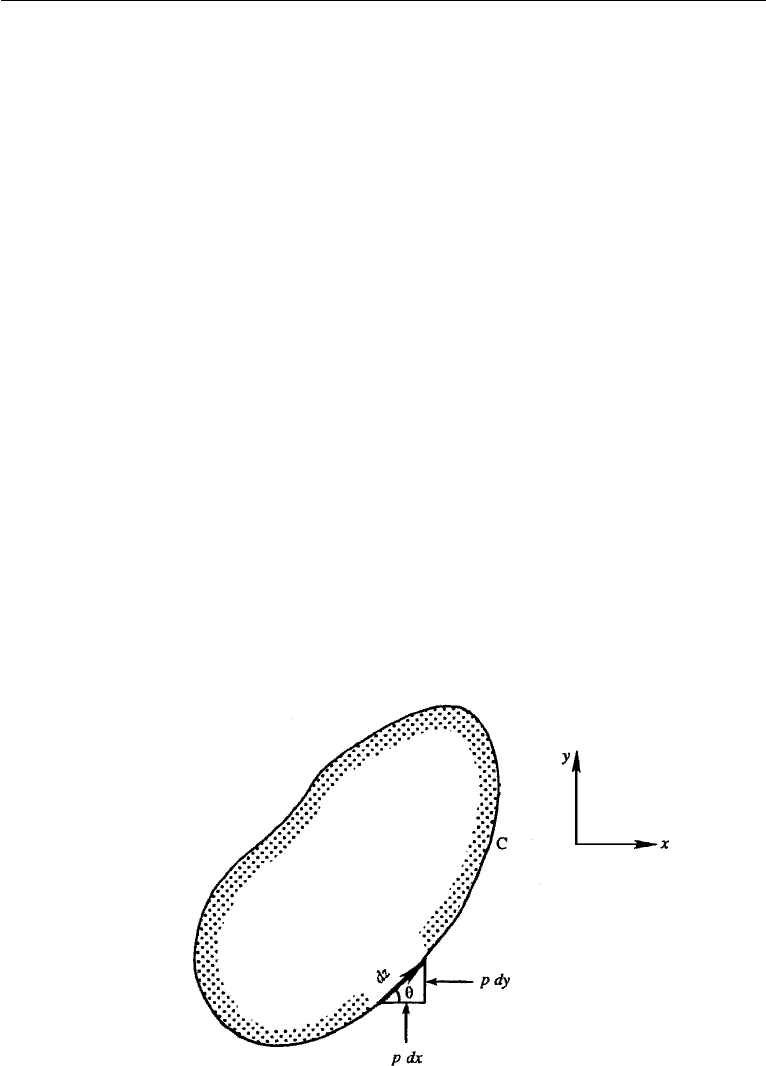
Consider a general cylindrical body, and let D and L be the x and y components of

the force exerted on it by the surrounding ﬂuid; we refer to D as “drag” and L as

“lift.” Because only normal pressures are exerted in inviscid ﬂows, the forces on a

surface element dz are (Figure 6.16)

dD =−pdy,

dL = pdx.

We form the complex quantity

dD −idL=−pdy− ip dx =−ip dz

∗

where an asterisk denotes the complex conjugate. The total force on the body is

therefore given by

D − iL =−i



pdz

∗

, (6.43)

Figure 6.16 Forces exerted on an element of a body.

11. Forces on a Two-Dimensional Body 185

where C denotes a counterclockwise contour coinciding with the body surface.

Neglecting gravity, the pressure is given by the Bernoulli equation

∞

ρU

= p +

ρ(u

+ v

) = p +

ρ(u + iv)(u − iv).

Substituting for p in equation (6.43), we obtain

D − iL =−i



∞

ρU

−

ρ(u + iv)(u − iv)]dz

∗

, (6.44)

Now the integral of the constant term (p

∞

ρU

) around a closed contour is zero.

Also, on the body surface the velocity vector and the surface element dz are parallel

(Figure 6.16), so that

u + iv =



+ v

iθ

dz =|dz|e

iθ

The product (u + iv)dz

∗

is therefore real, and we can equate it to its complex

conjugate:

(u + iv)dz

∗

= (u − iv)dz.

Equation (6.44) then becomes

D − iL =







dz, (6.45)

where we have introduced the complex velocity dw/dz = u −iv. Equation (6.45)

is called the Blasius theorem, and applies to any plane steady irrotational ﬂow. The

integral need not be carried out along the contour of the body because the theory

of complex variables shows that any contour surrounding the body can be chosen,

provided that there are no singularities between the body and the contour chosen.

Kutta–Zhukhovsky Lift Theorem

We now apply the Blasius theorem to a steady ﬂowaround an arbitrary cylindricalbody,

around which there is a clockwise circulation . The velocity at inﬁnity has a magni-

tude U and is directed along the x-axis. The ﬂow can be considered a superposition

of a uniform stream and a set of singularities such as vortex, doublet, source, and sink.

As there are no singularities outside the body, we shall take the contour C in

the Blasius theorem at a very large distance from the body. From large distances, all

singularities appear to be located near the origin z = 0. The complex potential is then

of the form

w = Uz +

2π

ln z +

i

2π

ln z +

+···.

The ﬁrst term represents a uniform ﬂow, the second term represents a source, the third

term represents a clockwise vortex, and the fourth term represents a doublet. Because

186 Irrotational Flow

the body contour is closed, the mass efﬂux of the sources must be absorbed by the

sinks. It follows that the sum of the strength of the sources and sinks is zero, thus we

should set m = 0. The Blasius theorem, equation (6.45), then becomes

D − iL =

iρ





U +

i

2πz

−

+···



dz. (6.46)

To carry out the contour integral in equation (6.46), we simply have to ﬁnd the

coefﬁcient of the term proportional to 1/z in the integrand. The coefﬁcient of 1/z in

a power series expansion for f(z)is called the residue of f(z)at z = 0. It is shown

in complex variable theory that the contour integral of a function f(z) around the

contour C is 2πi times the sum of the residues at the singularities within C:



f(z)dz = 2πi[sum of residues].

The residue of the integrand in equation (6.46) is easy to ﬁnd. Clearly the term µ/z

does not contribute to the residue. Completing the square (U +i/2πz)

, we see that

the coefﬁcient of 1/z is i U/π. This gives

D − iL =

iρ



2πi



iU



which shows that

D = 0,

L = ρU.

(6.47)

The ﬁrst of these equations states that there is no drag experienced by a body in

steady two-dimensional irrotational ﬂow. The second equation shows that there is a

lift force L = ρU perpendicular to the stream, experienced by a two-dimensional

body of arbitrary cross section. This result is called the Kutta–Zhukhovsky lift the-

orem, which was demonstrated in the preceding section for ﬂow around a circular

cylinder. The result will play a fundamental role in our study of ﬂow around airfoil

shapes (Chapter 15). We shall see that the circulation developed by an airfoil is nearly

proportional to U, so that the lift is nearly proportional to U

The following points can also be demonstrated. First, irrotational ﬂow over a

ﬁnite three-dimensional object has no circulation, and there can be no net force on

the body in steady state. Second, in an unsteady ﬂow a force is required to push a body,

essentially because a mass of ﬂuid has to be accelerated from rest.

Let us redrive the Kutta–Zhukhovsky lift theorem from considerations of vector

calculus without reference to complex variables. From equations (4.28) and (4.33),

for steady ﬂow with no body forces, and with I the dyadic equivalent of the Kronecker

delta δ

=−



(ρuu + pI − σ) · dA

11. Forces on a Two-Dimensional Body 187

Assuming an inviscid ﬂuid, σ = 0. Now additionally assume a two-dimensional

constant density ﬂow that is uniform at inﬁnity u = Ui

. Then, from Bernoulli’s

theorem, p + ρq

/2 = p

∞

+ ρq

/2 = p

,sop = p

− ρq

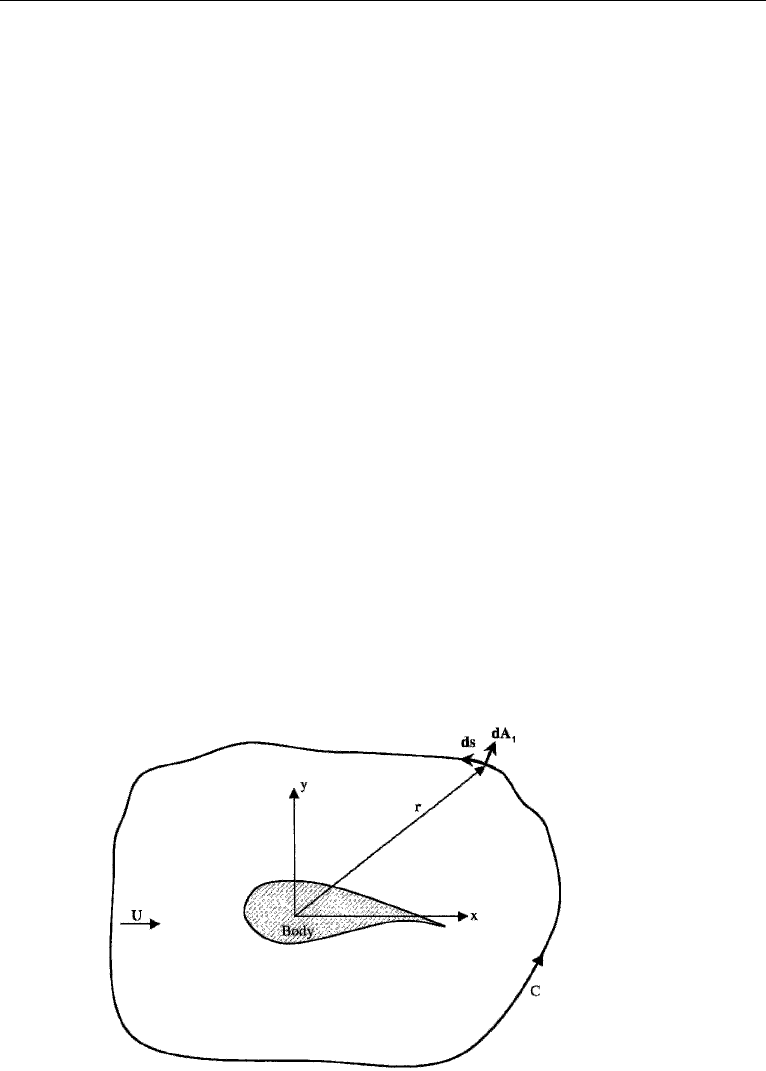
/2. Referring to

Figure 6.17, for two-dimensional ﬂow dA

= ds×i

dz, where here z is the coordinate

out of the paper. We will carry out the integration over a unit depth in z so that the

result for F

will be force per unit depth (in z).

With r = xi

+yi

, dr = dxi

+dyi

= ds, dA

= ds ×i

·1 =−i

dx+i

dy.

Now let u = U i

+ u



, where u



→ 0asr →∞at least as fast as 1/r. Substituting

for uu and q

in the integral for F

,weﬁnd

=−ρ



{UUi

+ U i



+ v



) + (u



+ v



+ u



+ (i

+ i

)[p

/ρ − U

/2 −Uu



− (u

2

+ v

2

)/2]} · (−i

dx + i

dy).

Let r →∞so that the contour C is far from the body. The constant terms U

/ρ, −U

/2 integrate to zero around the closed path. The quadratic terms u



2

+ v

2

)/2  1/r

as r →∞and the perimeter of the contour increases only

as r. Thus the quadratic terms → 0asr →∞. Separating the force into x and y

components,

=−i

ρU



[(u



dy − v



dx) + (u



dy − u



dy)]−i

ρU





dy + u



dx).

We note that the ﬁrst integrand is u



· ds × i

, and that we may add the constant

to each of the integrands because the integration of a constant velocity over a

Figure 6.17 Domain of integration for the Kutta–Zhukhovsky theorem.

188 Irrotational Flow

closed contour or surface will result in zero force. The integrals for the force then

become

=−i

ρU



(Ui

+ u



) · dA

− i

ρU



(Ui

+ u



) · ds.

The ﬁrst integral is zero by equation (4.29) (as a consequence of mass conser-

vation for constant density ﬂow) and the second is the circulation  by deﬁnition.

Thus,

=−i

ρU (force/unit depth),

where  is positive in the counterclockwise sense. We see that there is no force

component in the direction of motion (drag) under the assumptions necessary for

the derivation (steady, inviscid, no body forces, constant density, two-dimensional,

uniform at inﬁnity) that were believed to be valid to a reasonable approximation for

a wide variety of ﬂows. Thus it was labeled a paradox—d’Alembert’s paradox (Jean

Le Rond d’Alembert, 16 November 1717–29 October 1783).

Unsteady Flow

The Euler momentum integral [(4.28)] can be extended to unsteady ﬂows as follows.

The extension may have some utility for constant density irrotational ﬂows with

moving boundaries; thus it is derived here.

Integrating (4.17) over a ﬁxed volume V bounded by a surface A(A = ∂V)

containing within it only ﬂuid particles, we obtain

d/dt



ρu dV =−



A =∂V

ρuu

•

dA +



A =∂V

•

where body forces g have been neglected, and the divergence theorem has been used.

Because the immersed body cannot be part of V , we take A = A

+ A

,as

shown in Figure 4.9. Here A

is a “distant” surface, A

is the body surface, and A

is the connection between A

and A

that we allow to vanish. We identiﬁed the force

on the immersed body as

=−



•

Then,

=−



(ρuu − τ)

•

−



ρuu

•

− d/dt



ρu dV (6.48)

If the ﬂow is unsteady because of a moving boundary (A

), then u

•

= 0, as we

showed at the end of Section 4.19. If the body surface is described by f (x, y, z,t) = 0,

then the condition that no mass of ﬂuid with local velocity u ﬂow across the boundary

is (4.92): Df/Dt = ∂f/∂t + u

•

∇f = 0. Since ∇f is normal to the boundary

12. Source near a Wall: Method of Images 189

(as is dA

), u

•

∇f =−∂f/∂t on f = 0. Thus u

•

is in general = 0 on the body

surface. Equation (6.48) may be simpliﬁed if the density ρ = const. and if viscous

effects can be neglected in the ﬂow. Then, by Kelvin’s theorem the ﬂow is circulation

preserving. If it is initially irrotational, it will remain so. With ∇×u = 0, u =∇φ and

ρ = const., the last integral in (6.48) can be transformed by the divergence theorem

d/dt



ρu dV = ρd/dt



∇φdV = ρd/dt



A =∂V

φI

•

With A = A

+ A

and A

→ 0, the A

and A

integrals can be combined

with the ﬁrst two integrals in (6.48) to yield

=−



(ρuu + pI + ρI∂φ∂t)

•

−



(ρuu + ρI∂φ/∂t)

•

, (6.49)

where τ =−pI +σ and σ = 0 with the neglect of viscosity. The Bernoulli equation

for unsteady irrotational ﬂow [(4.81)], ρ∂φ/∂t +p +ρu

/2 = 0, where the function

of integration F(t) has been absorbed in the φ, can be used if desired to achieve a

slightly different form.

12. Source near a Wall: Method of Images

The method of images is a way of determining a ﬂow ﬁeld due to one or more

singularities near a wall. It was introduced in Chapter 5, Section 8, where vortices

near a wall were examined. We found that the ﬂow due to a line vortex near a wall can

be found by omitting the wall and introducing instead a vortex of opposite strength

at the “image point.” The combination generates a straight streamline at the location

of the wall, thereby satisfying the boundary condition.

Another example of this technique is given here, namely, the ﬂow due to a line

source at a distance a from a straight wall. This ﬂow can be simulated by introducing

an image source of the same strength and sign, so that the complex potential is

w =

2π

ln (z − a) +

2π

ln (z + a) −

2π

ln a

2π

ln (x

− y

− a

+ i2xy) −

2π

ln a

. (6.50)

We know that the logarithm of any complex quantity ζ =|ζ |exp (iθ ) can be written

as ln ζ = ln |ζ |+iθ. The imaginary part of equation (6.50) is therefore

ψ =

2π

tan

−1

2xy

− y

− a

from which the equation of streamlines is found as

− y

− 2xy cot



2πψ



= a

190 Irrotational Flow

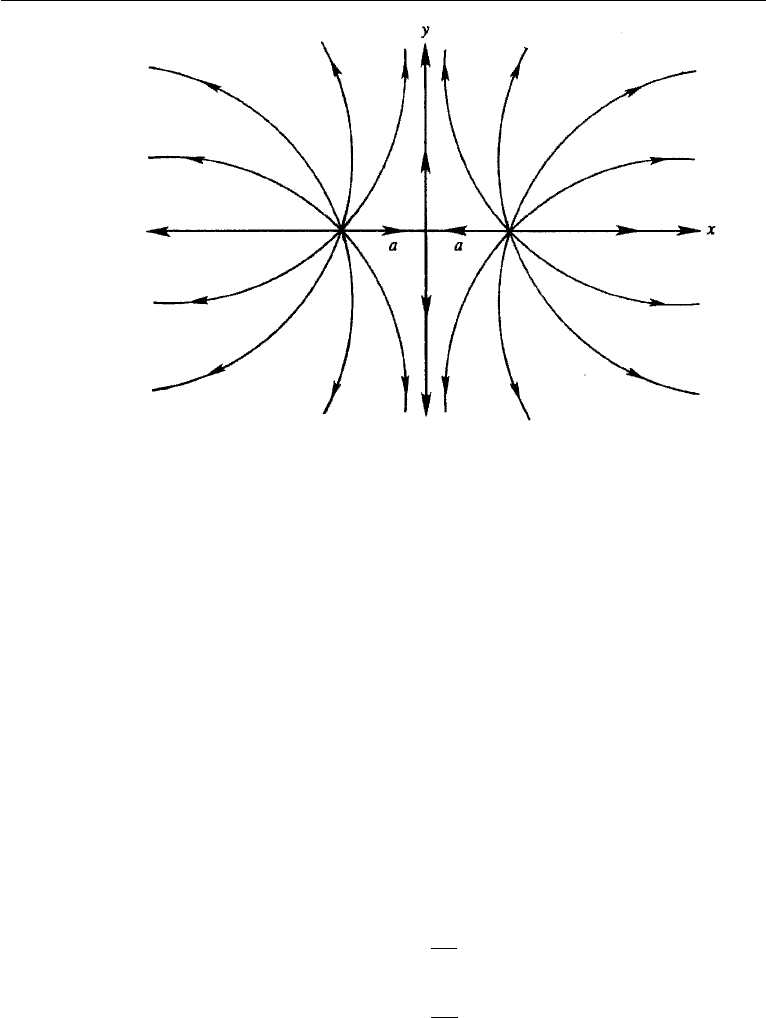
Figure 6.18 Irrotational ﬂow due to two equal sources.

The streamline pattern is shown in Figure 6.18. The x and y axes form part of the

streamline pattern, with the origin as a stagnation point. It is clear that the complex

potential equation (6.48) represents three interesting ﬂow situations:

(1) ﬂow due to two equal sources (entire Figure 6.18);

(2) ﬂow due to a source near a plane wall (right half of Figure 6.18); and

(3) ﬂow through a narrow slit in a right-angled wall (ﬁrst quadrant of Figure 6.18).

13. Conformal Mapping

We shall now introduce a method by which complex ﬂow patterns can be transformed

into simple ones using a technique known as conformal mapping in complex variable

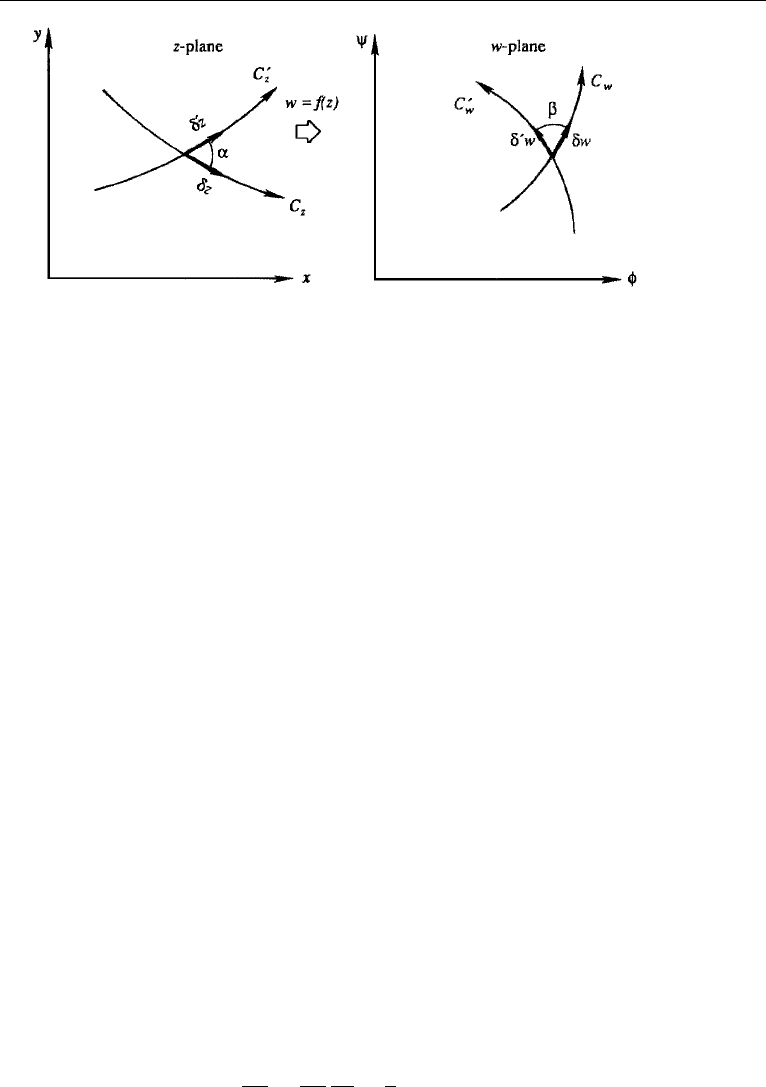
theory. Consider the functional relationship w =f(z), which maps a point in the

w-plane to a point in the z-plane, and vice versa. We shall prove that inﬁnitesimal

ﬁgures in the two planes preserve their geometric similarity if w = f(z)is analytic.

Let lines C

and C



in the z-plane be transformations of the curves C

and C



in the

w-plane, respectively (Figure 6.19). Let δz, δ



z, δw, and δ



w be inﬁnitesimal elements

along the curves as shown. The four elements are related by

δw =

δz, (6.51)



w =



z. (6.52)

If w = f(z) is analytic, then dw/dz is independent of orientation of the elements,

and therefore has the same value in equation (6.51) and (6.52). These two equations

13. Conformal Mapping 191

Figure 6.19 Preservation of geometric similarity of small elements in conformal mapping.

then imply that the elements δz and δ



z are rotated by the same amount (equal to the

argument of dw/dz) to obtain the elements δw and δ



w. It follows that

α = β,

which demonstrates that inﬁnitesimal ﬁgures in the two planes are geometrically

similar. The demonstration fails at singular points at which dw/dz is either zero or

inﬁnite. Because dw/dz is a function of z, the amount of magniﬁcation and rotation

that an element δz undergoes during transformation from the z-plane to the w-plane

varies. Consequently, large ﬁgures become distorted during the transformation.

In application of conformal mapping, we always choose a rectangular grid in the

w-plane consisting of constant φ and ψ lines (Figure 6.20). In other words, we deﬁne

φ and ψ to be the real and imaginary parts of w:

w = φ + iψ.

The rectangular net in the w-plane represents a uniform ﬂow in this plane. The con-

stant φ and ψ lines are transformed into certain curves in the z-plane through the

transformation w = f(z). The pattern in the z-plane is the physical pattern under

investigation, and the images of constant φ and ψ lines in the z-plane form the equipo-

tential lines and streamlines, respectively, of the desired ﬂow. We say that w = f(z)

transforms a uniform ﬂow in the w-plane into the desired ﬂow in the z-plane. In fact,

all the preceding ﬂow patterns studied through the transformation w = f(z)can be

interpreted this way.

If the physical pattern under investigation is too complicated, we may introduce

intermediate transformations in going from the w-plane to the z-plane. For example,

the transformation w = ln (sin z) can be broken into

w = ln ζζ= sin z.

Velocity components in the z-plane are given by

u − iv =

dζ

cos z = cot z.