Cohen I.M., Kundu P.K. Fluid Mechanics
Подождите немного. Документ загружается.

172 Irrotational Flow
y
x
h
-m
m
a
a
x
s
x
s
U
Figure 6.4 Irrotational flow at a wall angle. Equipotential lines are dashed.
Figure 6.5 Stagnation flow represented by w = Az
2
.
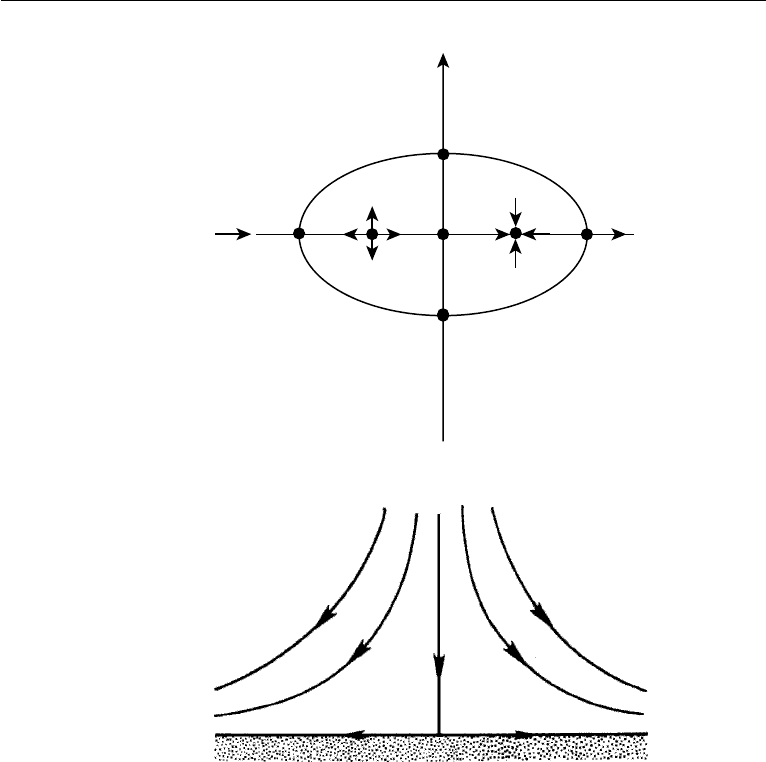
which shows that at the origin dw/dz = 0 for α<π, and dw/dz =∞for α>π.
Thus, the corner is a stagnation point for flow in a wall angle smaller than 180
◦
;
in contrast, it is a point of infinite velocity for wall angles larger than 180
◦
. In both
cases the origin is a singular point.
The pattern for n = 1/2 corresponds to flow around a semi-infinite plate. When
n = 2, the pattern represents flow in a region bounded by perpendicular walls. By
including the field within the second quadrant of the z-plane, it is clear that n = 2
also represents the flow impinging against a flat wall (Figure 6.5). The streamlines
and equipotential lines are all rectangular hyperbolas. This is called a stagnation flow
because it represents flow in the neighborhood of the stagnation point of a blunt body.
Real flows near a sharp change in wall slope are somewhat different than those
shown in Figure 6.4. For n<1 the irrotational flow velocity is infinite at the ori-
gin, implying that the boundary streamline (ψ = 0) accelerates before reaching
5. Sources and Sinks 173
this point and decelerates after it. Bernoulli’s equation implies that the pressure
force downstream of the corner is “adverse” or against the flow. It will be shown
in Chapter 10 that an adverse pressure gradient causes separation of flow and gener-
ation of stationary eddies. A real flow in a corner with an included angle larger than
180
◦
would therefore separate at the corner (see the right panel of Figure 6.2).
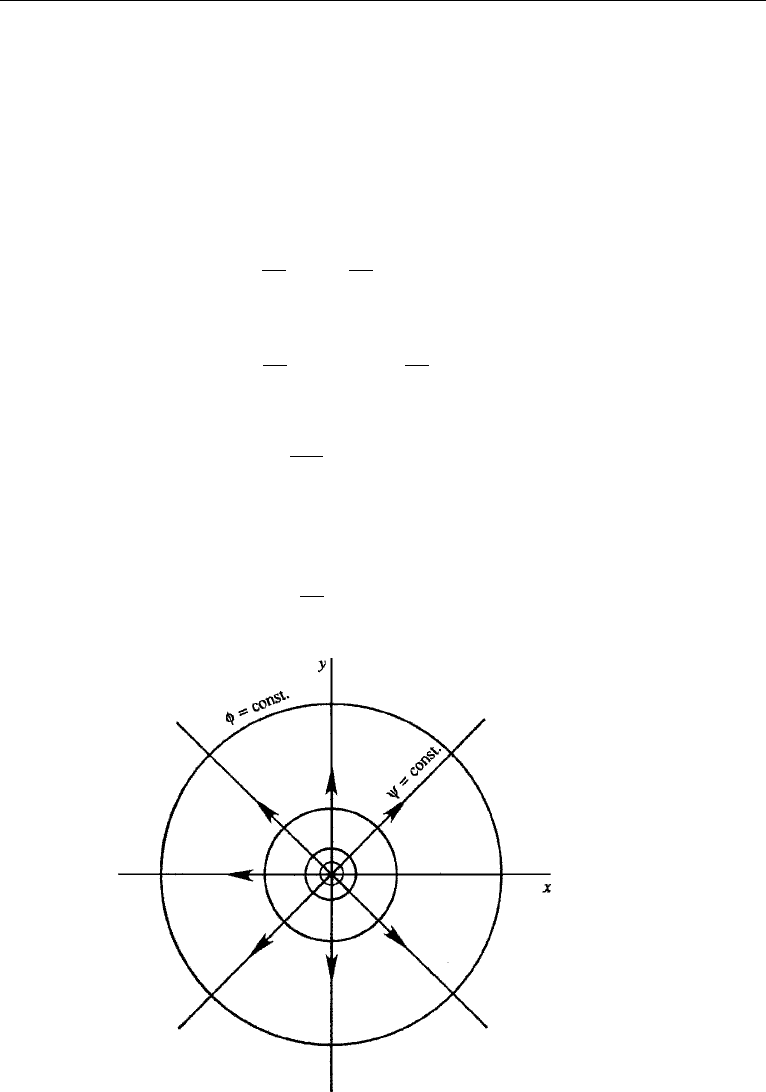
5. Sources and Sinks
Consider the complex potential
w =
m
2π
ln z =
m
2π
ln (re
iθ
). (6.22)
The real and imaginary parts are
φ =
m
2π
ln rψ=
m
2π
θ, (6.23)
from which the velocity components are found as
u
r
=
m
2πr
u
θ
= 0. (6.24)
This clearly represents a radial flow from a two-dimensional line source at the origin,
with a volume flow rate per unit depth of m (Figure 6.6). The flow represents a line
sink if m is negative. For a source situated at z = a, the complex potential is
w =
m
2π
ln (z − a). (6.25)
Figure 6.6 Plane source.
174 Irrotational Flow
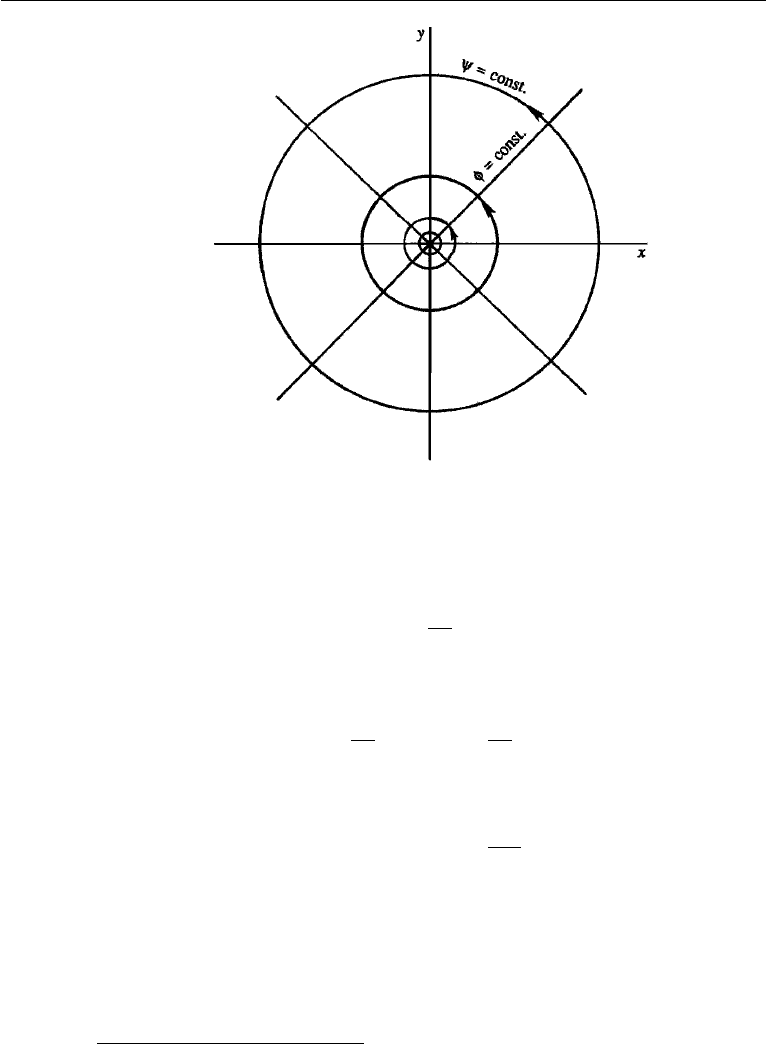
Figure 6.7 Plane irrotational vortex.
6. Irrotational Vortex
The complex potential
w =−
i
2π
ln z. (6.26)
represents a line vortex of counterclockwise circulation . Its real and imaginary
parts are
φ =
2π
θψ=−
2π
ln r, (6.27)
1
from which the velocity components are found to be
u
r
= 0 u
θ
=
2πr
. (6.28)
The flow pattern is shown in Figure 6.7.
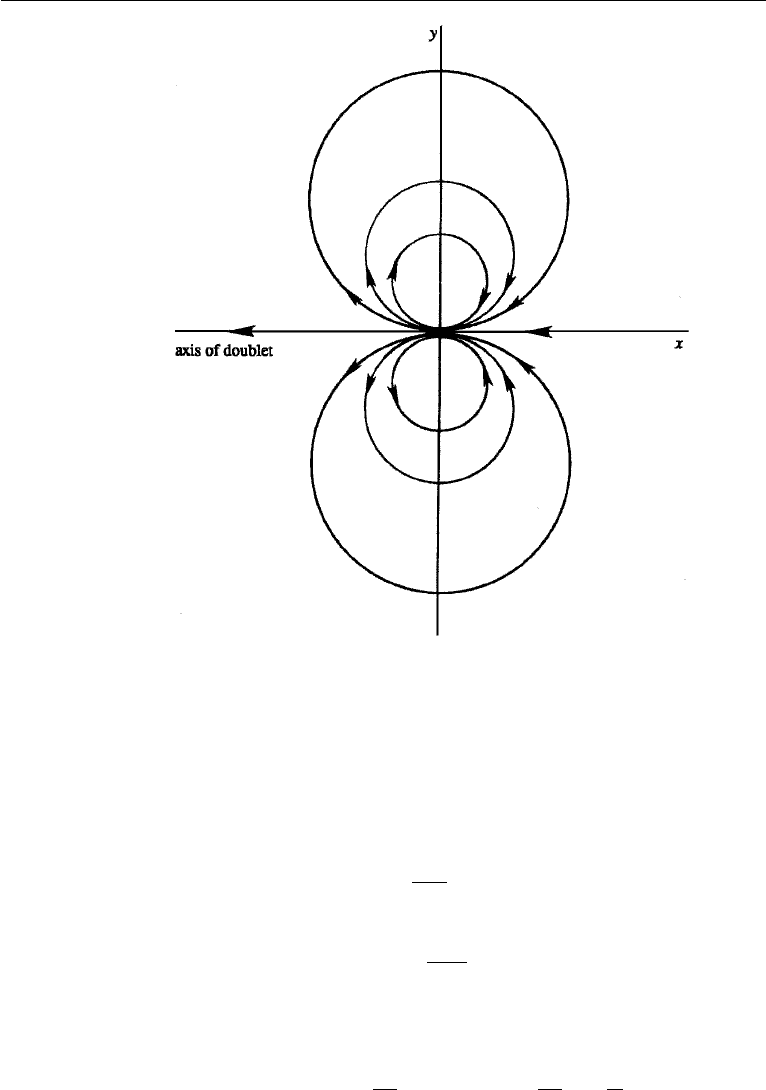
7. Doublet
A doublet or dipole is obtained by allowing a source and a sink of equal strength
to approach each other in such a way that their strengths increase as the separation
1
The argument of transcendental functions such as the logarithm must always be dimensionless. Thus a
constant must be added to ψ in equation (6.27) to put the logarithm in proper form. This is done explicitly
when we are solving a problem as in Section 10 in what follows.

8. Flow past a Half-Body 175
distance goes to zero, and that the product tends to a finite limit. The complex potential
for a source-sink pair on the x-axis, with the source at x =−ε and the sink at x = ε,is
w =
m
2π
ln (z + ε) −
m
2π
ln (z − ε) =
m
2π
ln
z + ε
z − ε
,
m
2π
ln
1 +
2ε
z
+···
mε
πz
.
Defining the limit of mε/π as ε → 0tobeµ, the preceding equation becomes
w =
µ
z
=
µ
r
e
−iθ
, (6.29)
whose real and imaginary parts are
φ =
µx
x
2
+ y
2
ψ =−
µy
x
2
+ y
2
. (6.30)
The expression for ψ in the preceding can be rearranged in the form
x
2
+
y +
µ
2ψ
2
=
µ
2ψ
2
.
The streamlines, represented by ψ = const., are therefore circles whose centers lie
on the y-axis and are tangent to the x-axis at the origin (Figure 6.8). Direction of
flow at the origin is along the negative x-axis (pointing outward from the source of
the limiting source-sink pair), which is called the axis of the doublet. It is easy to
show that (Exercise 1) the doublet flow equation (6.29) can be equivalently defined
by superposing a clockwise vortex of strength − on the y-axis at y = ε, and a
counterclockwise vortex of strength at y =−ε.
The complex potentials for concentrated source, vortex, and doublet are all sin-
gular at the origin. It will be shown in the following sections that several interesting
flow patterns can be obtained by superposing a uniform flow on these concentrated
singularities.
8. Flow past a Half-Body
An interesting flow results from superposition of a source and a uniform stream. The
complex potential for a uniform flow of strength U is w = Uz, which follows from
integrating the relation dw/dz = u − iv. Adding to that, the complex potential for a
source at the origin of strength m, we obtain,
w = Uz +
m
2π
ln z, (6.31)
whose imaginary part is
ψ = Ur sin θ +
m
2π
θ. (6.32)
176 Irrotational Flow
Figure 6.8 Plane doublet.
From equations (6.12) and (6.13) it is clear that there must be a stagnation point to
the left of the source (S in Figure 6.9), where the uniform stream cancels the velocity
of flow from the source. If the polar coordinate of the stagnation point is (a,π), then
cancellation of velocity requires
U −
m
2πa
= 0,
giving
a =
m
2πU
.
(This result can also be found by finding dw/dz and setting it to zero.) The value of
the streamfunction at the stagnation point is therefore
ψ
s
= Ur sin θ +
m
2π
θ = Ua sin π +
m
2π
π =
m
2
.

8. Flow past a Half-Body 177
Figure 6.9 Irrotational flow past a two-dimensional half-body. The boundary streamline is given by
ψ = m/2.
The equation of the streamline passing through the stagnation point is obtained by
setting ψ = ψ
s
= m/2, giving
Ur sin θ +
m
2π
θ =
m
2
. (6.33)
A plot of this streamline is shown in Figure 6.9. It is a semi-infinite body with a
smooth nose, generally called a half-body. The stagnation streamline divides the field
into a region external to the body and a region internal to it. The internal flow consists
entirely of fluid emanating from the source, and the external region contains the
originally uniform flow. The half-body resembles several practical shapes, such as
the front part of a bridge pier or an airfoil; the upper half of the flow resembles the
flow over a cliff or a side contraction in a wide channel.
The half-width of the body is found to be
h = r sin θ =
m(π −θ)
2πU
,
where equation (6.33) has been used. The half-width tends to h
max
= m/2U as θ → 0
(Figure 6.9). (This result can also be obtained by noting that mass flux from the source
is contained entirely within the half-body, requiring the balance m = (2h
max
)U at
a large downstream distance where u = U .)
The pressure distribution can be found from Bernoulli’s equation
p +
1
2
ρq
2
= p
∞
+
1
2
ρU
2
.
A convenient way of representing pressure is through the nondimensional excess
pressure (called pressure coefficient)
C
p
≡
p − p
∞
1
2
ρU
2
= 1 −
q
2
U
2
.
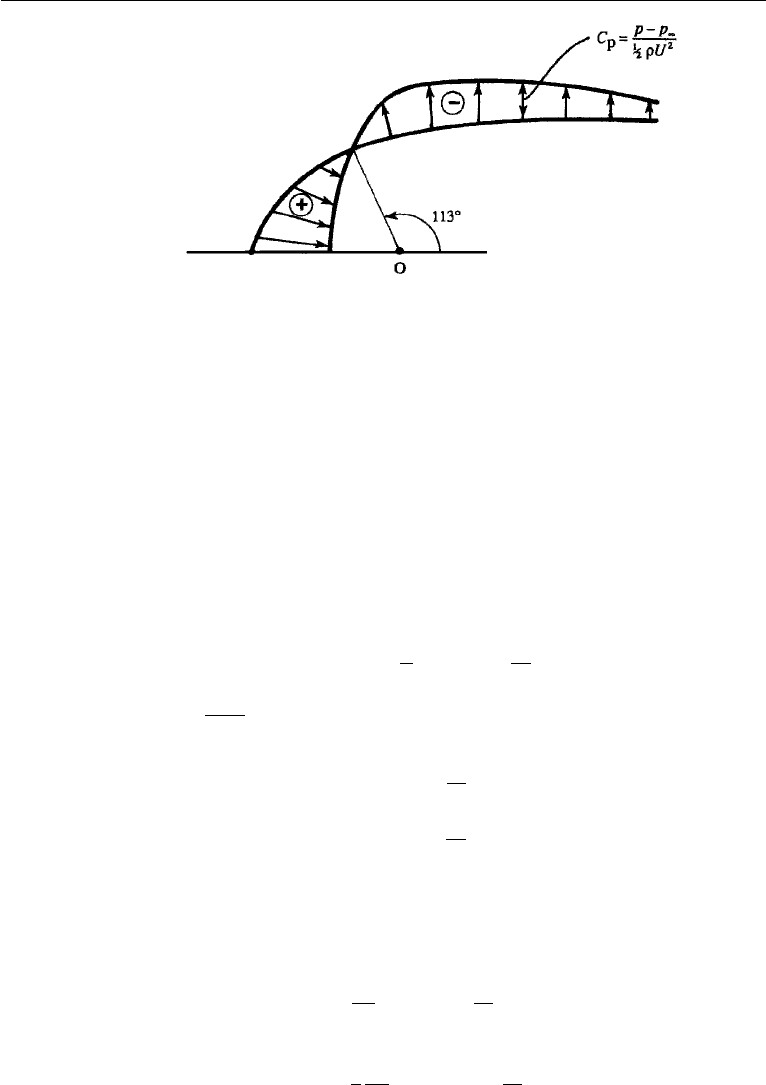
178 Irrotational Flow
Figure 6.10 Pressure distribution in irrotational flow over a half-body. Pressure excess near the nose is
indicated by ⊕ and pressure deficit elsewhere is indicated by .
A plot of C
p
on the surface of the half-body is given in Figure 6.10, which shows
that there is pressure excess near the nose of the body and a pressure deficit beyond
it. It is easy to show by integrating p over the surface that the net pressure force is
zero (Exercise 2).
9. Flow past a Circular Cylinder without Circulation
Combination of a uniform stream and a doublet with its axis directed against the
stream gives the irrotational flow over a circular cylinder. The complex potential for
this combination is
w = Uz +
µ
z
= U
z +
a
2
z
, (6.34)
where a ≡
√
µ/U . The real and imaginary parts of w give
φ = U
r +
a
2
r
cos θ
ψ = U
r −
a
2
r
sin θ.
(6.35)
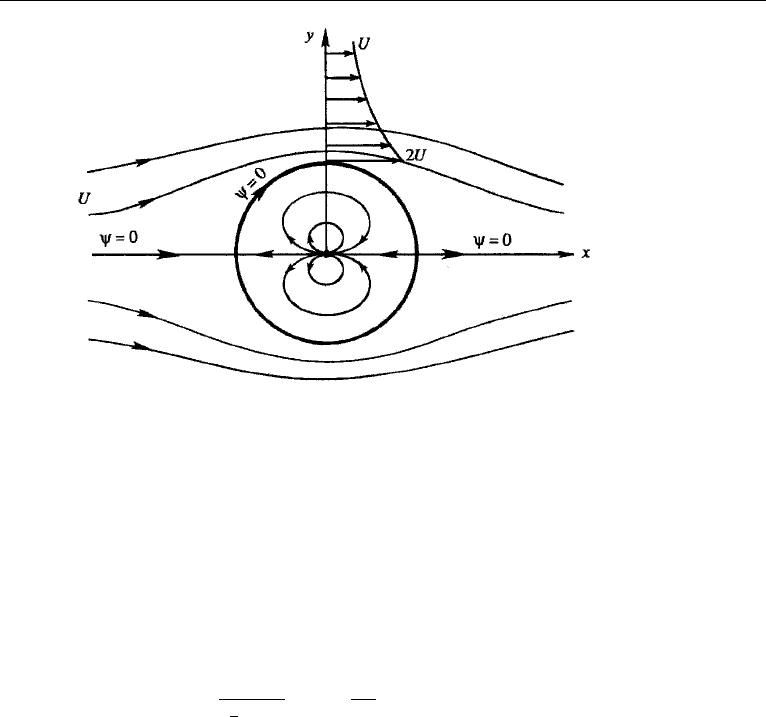
It is seen that ψ = 0atr = a for all values of θ , showing that the streamline
ψ = 0 represents a circular cylinder of radius a. The streamline pattern is shown in
Figure 6.11. Flow inside the circle has no influence on that outside the circle. Velocity
components are
u
r
=
∂φ
∂r
= U
1 −
a
2
r
2
cos θ.
u
θ
=
1
r
∂φ
∂θ
=−U
1 +
a
2
r
2
sin θ,
9. Flow past a Circular Cylinder without Circulation 179
Figure 6.11 Irrotational flow past a circular cylinder without circulation.
from which the flow speed on the surface of the cylinder is found as
q|
r =a
=|u
θ
|
r =a
= 2U sin θ, (6.36)
where what is meant is the positive value of sin θ. This shows that there are stagnation
points on the surface, whose polar coordinates are (a, 0) and (a, π). The flow reaches
a maximum velocity of 2 U at the top and bottom of the cylinder.
Pressure distribution on the surface of the cylinder is given by
C
p
=
p − p
∞
1
2
ρU
2
= 1 −
q
2
U
2
= 1 −4 sin
2
θ.
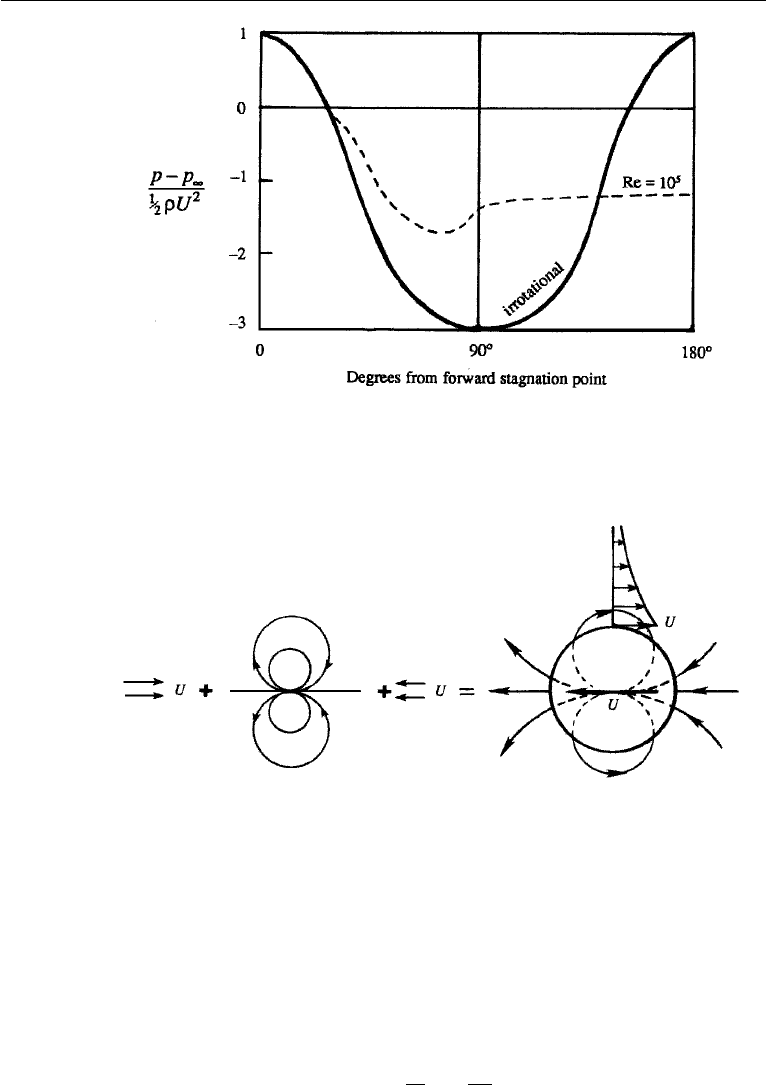
Surface distribution of pressure is shown by the continuous line in Figure 6.12. The
symmetry of the distribution shows that there is no net pressure drag. In fact, a general
result of irrotational flow theory is that a steadily moving body experiences no drag.
This result is at variance with observations and is sometimes known as d’Alembert’s
paradox. The existence of tangential stress, or “skin friction,” is not the only reason
for the discrepancy. For blunt bodies, the major part of the drag comes from separation
of the flow from sides and the resulting generation of eddies. The surface pressure in
the wake is smaller than that predicted by irrotational flow theory (Figure 6.12),
resulting in a pressure drag. These facts will be discussed in further detail in
Chapter 10.
The flow due to a cylinder moving steadily through a fluid appears unsteady to
an observer at rest with respect to the fluid at infinity. This flow can be obtained by
superposing a uniform stream along the negative x direction to the flow shown in
Figure 6.11. The resulting instantaneous flow pattern is simply that of a doublet, as
is clear from the decomposition shown in Figure 6.13.
180 Irrotational Flow
Figure 6.12 Comparison of irrotational and observed pressure distributions over a circular cylinder. The
observed distribution changes with the Reynolds number Re; a typical behavior at high Re is indicated by
the dashed line.
Figure 6.13 Decomposition of irrotational flow pattern due to a moving cylinder.
10. Flow past a Circular Cylinder with Circulation
It was seen in the last section that there is no net force on a circular cylinder in steady
irrotational flow without circulation. It will now be shown that a lateral force, akin
to a lift force on an airfoil, results when circulation is introduced into the flow. If
a clockwise line vortex of circulation − is added to the irrotational flow around
a circular cylinder, the complex potential becomes
w = U
z +
a
2
z
+
i
2π
ln (z/a), (6.37)
10. Flow past a Circular Cylinder with Circulation 181
whose imaginary part is
ψ = U
r −
a
2
r
sin θ +
2π
ln (r/a), (6.38)
where we have added to w the term −(i/2π)ln a so that the argument of the loga-
rithm is dimensionless, as it must be always.
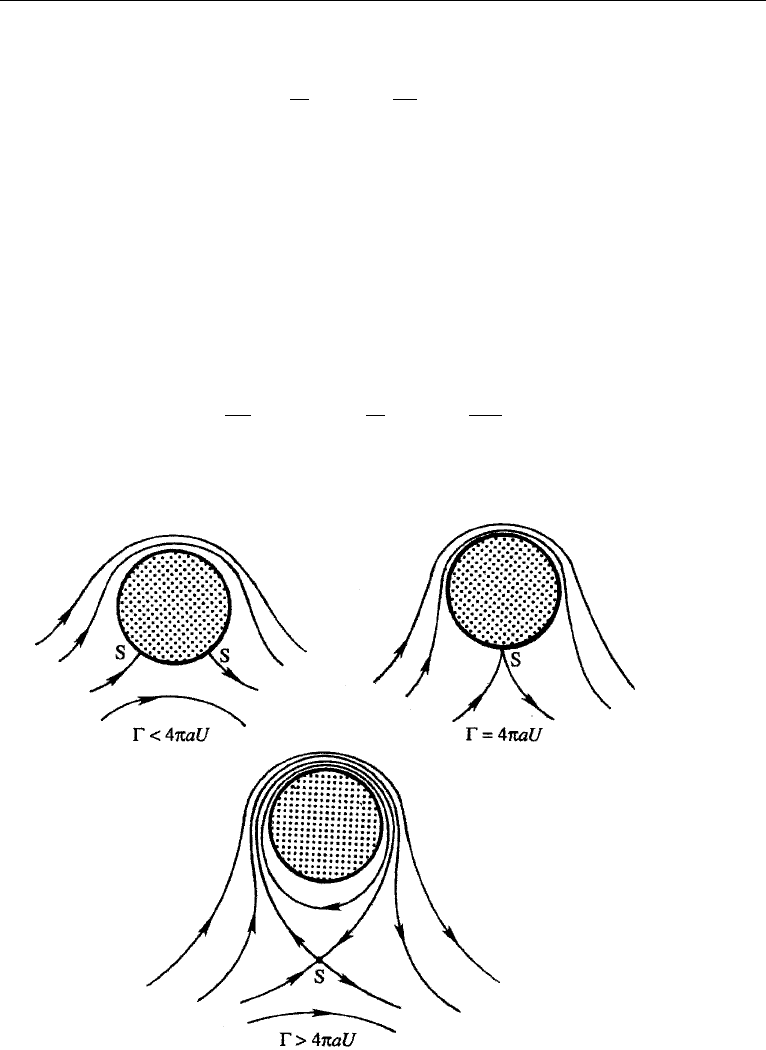
Figure 6.14 shows the resulting streamline pattern for various values of . The
close streamline spacing and higher velocity on top of the cylinder is due to the
addition of velocity fields of the clockwise vortex and the uniform stream. In contrast,
the smaller velocities at the bottom of the cylinder are a result of the vortex field
counteracting the uniform stream. Bernoulli’s equation consequently implies a higher
pressure below the cylinder and an upward “lift” force.
The tangential velocity component at any point in the flow is
u
θ
=−
∂ψ
∂r
=−U
1 +
a
2
r
2
sin θ −
2πr
.
Figure 6.14 Irrotational flow past a circular cylinder for different values of circulation. Point S represents
the stagnation point.
