Cohen I.M., Kundu P.K. Fluid Mechanics

Подождите немного. Документ загружается.

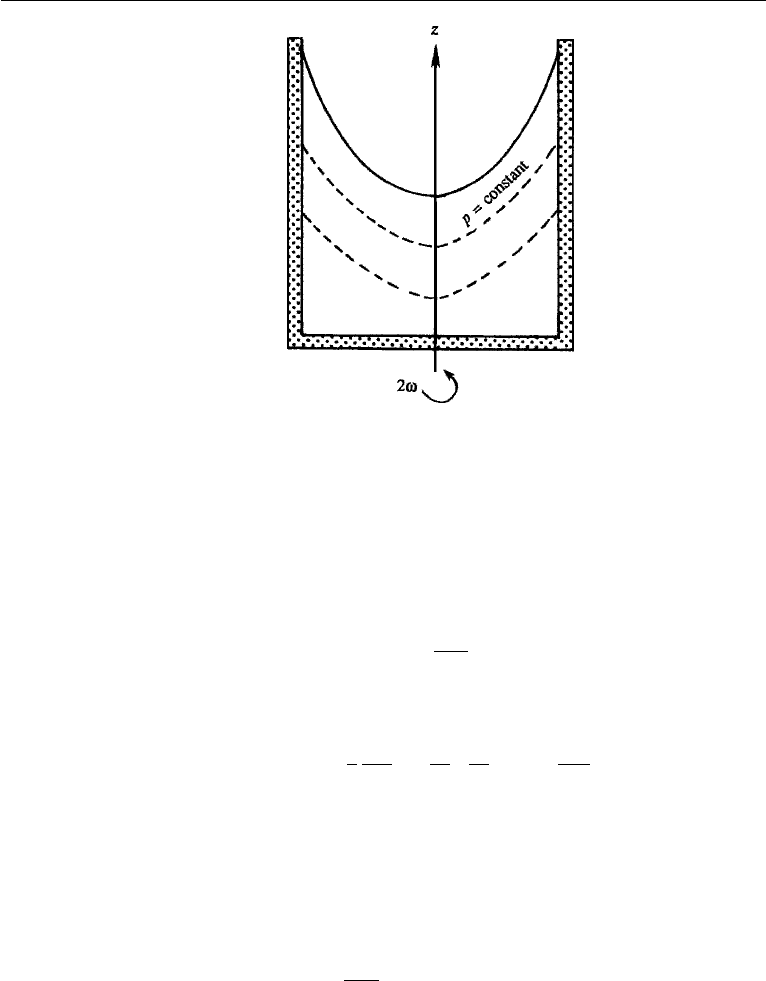
142 Vorticity Dynamics

Figure 5.2 Constant pressure surfaces in a solid-body rotation generated in a rotating tank containing

liquid.

which shows that the Bernoulli function B = u

/2 +gz + p/ρ is not constant for

points on different streamlines. This is expected of inviscid rotational ﬂows.

Irrotational Vortex

In an irrotational vortex represented by



2πr

the viscous stress is

rθ

= µ



∂u

∂θ

+ r

∂

∂r







=−

µ

πr

which is nonzero everywhere. This is because ﬂuid elements do undergo deformation

in such a ﬂow, as discussed in Chapter 3. However, the interesting point is that the net

viscous force on an element again vanishes, just as in the case of solid body rotation.

In an incompressible ﬂow, the net viscous force per unit volume is related to vorticity

by (see equation 4.48)

∂σ

∂x

=−µ(∇ × ω)

, (5.6)

which is zero for irrotational ﬂows. The viscous forces on the surfaces of an element

cancel out, leaving a zero resultant. The equations of motion therefore reduce to

the inviscid Euler equations, although viscous stresses are nonzero everywhere. The

3. Role of Viscosity in Rotational and Irrotational Vortices 143

pressure distribution can therefore be found from the inviscid set (5.4), giving

dp =

ρ

4π

dr − ρg dz,

where we have used u

= /(2πr). Integration between any two points gives

− p

=−

θ2

− u

θ1

) − ρg(z

− z

which implies

θ1

+ gz

θ2

+ gz

This shows that Bernoulli’s equation is applicable between any two points in the ﬂow

ﬁeld and not necessarily along the same streamline, as would be expected of inviscid

irrotational ﬂows. Surfaces of constant pressure are given by

− z

θ1

−

θ2



8π



−



which are hyperboloids of revolution of the second degree (Figure 5.3). Flow is

singular at the origin, where there is an inﬁnite velocity discontinuity. Consequently,

a real vortex such as that found in the atmosphere or in a bathtub necessarily has a

rotational core (of radius R, say) in the center where the velocity distribution can be

idealized by u

= ωr/2. Outside the core the ﬂow is nearly irrotational and can be

idealized by u

= ωR

/2r; here we have chosen the value of circulation such that u

is continuous at r = R (see Figure 3.17b). The strength of such a vortex is given by

 = (vorticity)(core area) = πωR

One way of generating an irrotational vortex is by rotating a solid circular cylinder

in an inﬁnite viscous ﬂuid (see Figure 9.7). It is shown in Chapter 9, Section 6 that

the steady solution of the Navier–Stokes equations satisfying the no-slip boundary

condition (u

= ωR/2atr = R)is

ωR

r  R,

where R is the radius of the cylinder and ω/2 is its constant angular velocity; see

equation (9.15). This ﬂow does not have any singularity in the entire ﬁeld and is

irrotational everywhere. Viscous stresses are present, and the resulting viscous dissi-

pation of kinetic energy is exactly compensated by the work done at the surface of

the cylinder. However, there is no net viscous force at any point in the steady state.

Discussion

The examples given in this section suggest that irrotationality does not imply the

absence of viscous stresses. In fact, they must always be present in irrotational ﬂows

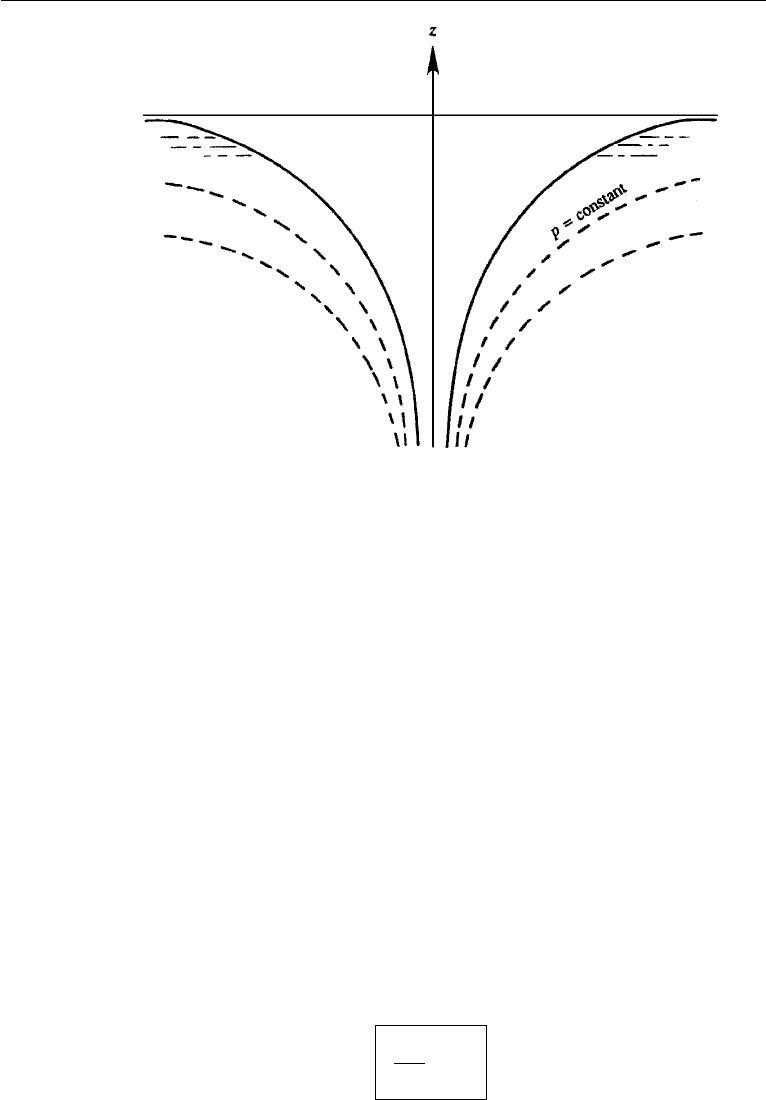
144 Vorticity Dynamics

Figure 5.3 Irrotational vortex in a liquid.

of real ﬂuids, simply because the ﬂuid elements deform in such a ﬂow. However

the net viscous force vanishes if ω = 0, as can be seen in equation (5.6). We have

also given an example, namely that of solid-body rotation, in which there is uniform

vorticity and no viscous stress at all. However, this is the only example in which

rotation can take place without viscous effects, because equation (5.6) implies that

the net force is zero in a rotational ﬂow if ω is uniform everywhere. Except for this

example, ﬂuid rotation is accomplished by viscous effects. Indeed, we shall see later

in this chapter that viscosity is a primary agent for vorticity generation.

4. Kelvin’s Circulation Theorem

Several theorems of vortex motion in an inviscid ﬂuid were published by Helmholtz

in 1858. He discovered these by analogy with electrodynamics. Inspired by this work,

Kelvin in 1868 introduced the idea of circulation and proved the following theorem:

In an inviscid, barotropic ﬂow with conservative body forces, the circulation around

a closed curve moving with the ﬂuid remains constant with time, if the motion is

observed from a nonrotating frame. The theorem can be restated in simple terms as

follows: At an instant of time take any closed contour C and locate the new position

of C by following the motion of all of its ﬂuid elements. Kelvin’s circulation theorem

states that the circulations around the two locations of C are the same. In other words,

D

= 0,

(5.7)

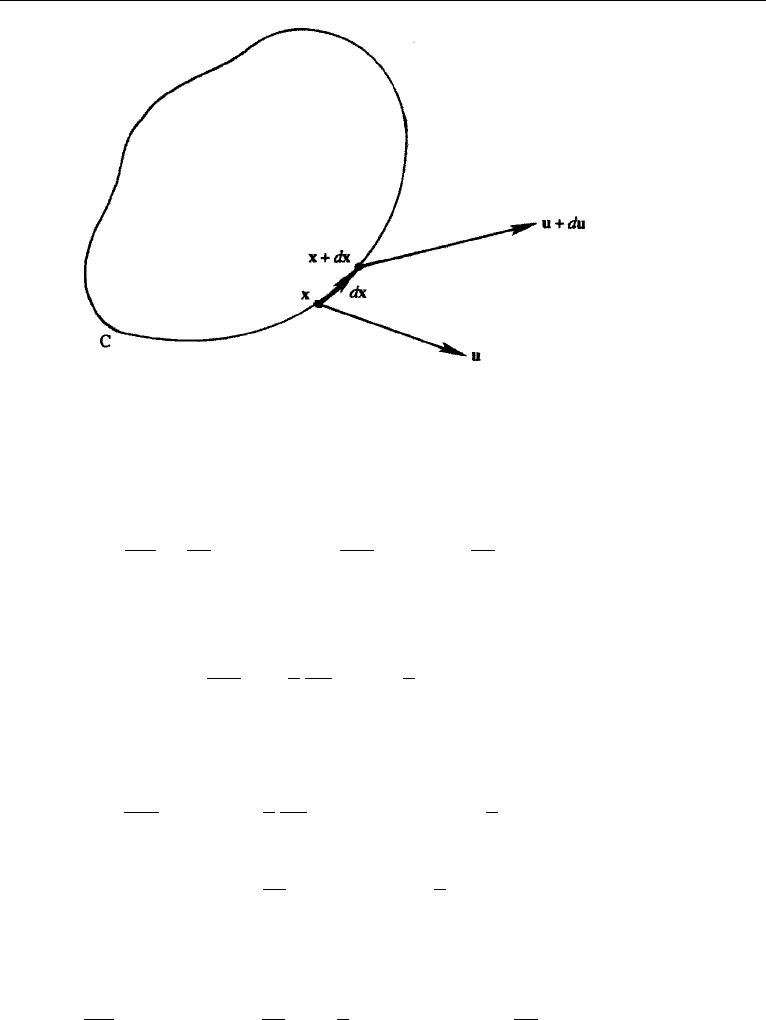
4. Kelvin’s Circulation Theorem 145

Figure 5.4 Proof of Kelvin’s circulation theorem.

where D/Dt has been used to emphasize that the circulation is calculated around a

material contour moving with the ﬂuid.

To prove Kelvin’s theorem, the rate of change of circulation is found as

D



(dx

), (5.8)

where dx is the separation between two points on C (Figure 5.4). Using the momentum

equation

=−

∂p

∂x

+ g

ij, j

where σ

is the deviatoric stress tensor (equation (4.33)). The ﬁrst integral in equa-

tion (5.8) becomes



=−



∂p

∂x



ij, j

=−



ij, j

where we have noted that dp = ∇p

•

dx is the difference in pressure between two

neighboring points. Equation (5.8) then becomes

D



•

dx −



(∇

•

σ)

•

dx +



(dx

). (5.9)

Each term of equation (5.9) will now be shown to be zero. Let the body force be

conservative, so that g =−∇, where  is the force potential or potential energy

146 Vorticity Dynamics

per unit mass. Then the line integral of g along a ﬂuid line AB is



•

dx =−



∇

•

dx =−



d = 

− 

When the integral is taken around the closed ﬂuid line, points A and B coincide,

showing that the ﬁrst integral on the right-hand side of equation (5.9) is zero.

Now assume that the ﬂow is barotropic, which means that density is a function

of pressure alone. Incompressible and isentropic (p/ρ

= constant for a perfect gas)

ﬂows are examples of barotropic ﬂows. In such a case we can write ρ

−1

as some

function of p, and we choose to write this in the form of the derivative ρ

−1

≡ dP /dp.

Then the integral of dp/ρ between any two points A and B can be evaluated, giving



dp = P

− P

The integral around a closed contour is therefore zero.

If viscous stresses can be neglected for those particles making up contour C, then

the integral of the deviatoric stress tensor is zero. To show that the last integral in

equation (5.9) vanishes, note that the velocity at point x + dx onCisgivenby

u + du =

(x + dx) =

(dx),

so that

du =

(dx),

The last term in equation (5.9) then becomes



(dx

) =







= 0.

This completes the proof of Kelvin’s theorem.

We see that the three agents that can create or destroy vorticity in a ﬂow are

nonconservative body forces, nonbarotropic pressure-density relations, and viscous

stresses. An example of each follows. A Coriolis force in a rotating coordinate system

generates the “bathtub vortex” when a ﬁlled tank, initially as rest on the earth’s

surface, is drained. Heating from below in a gravitational ﬁeld creates a buoyant force

generating an upward plume. Cooling from above and mass conservation require that

the motion be in cyclic rolls so that vorticity is created. Viscous stresses create vorticity

in the neighborhood of a boundary where the no-slip condition is maintained. A short

distance away from the boundary, the tangential velocity may be large. Then, because

there are large gradients transverse to the ﬂow, vorticity is created.

4. Kelvin’s Circulation Theorem 147

Discussion of Kelvin’s Theorem

Because circulation is the surface integral of vorticity, Kelvin’s theorem essentially

shows that irrotational ﬂows remain irrotational if the four restrictions are satisﬁed:

(1) Inviscid ﬂow: In deriving the theorem, the inviscid Euler equation has been

used, but only along the contour C itself. This means that circulation is pre-

served if there are no net viscous forces along the path followed by C. If C

moves into viscous regions such as boundary layers along solid surfaces, then

the circulation changes. The presence of viscous effects causes a diffusion of

vorticity into or out of a ﬂuid circuit, and consequently changes the circulation.

(2) Conservative body forces: Conservative body forces such as gravity act through

the center of mass of a ﬂuid particle and therefore do not tend to rotate it.

(3) Barotropic ﬂow: The third restriction on the validity of Kelvin’s theorem is that

density must be a function of pressure only. A homogeneous incompressible

liquid for which ρ is constant everywhere and an isentropic ﬂow of a perfect

gas for which p/ρ

is constant are examples of barotropic ﬂows. Flows that are

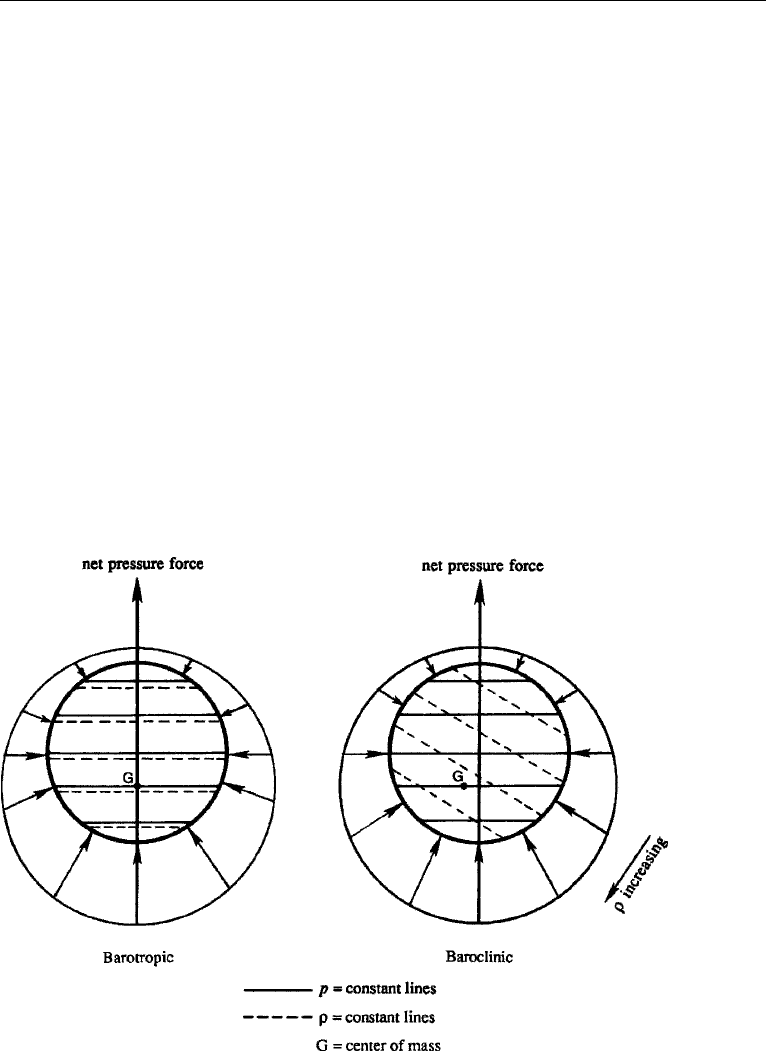
not barotropic are called baroclinic. Consider ﬂuid elements in barotropic and

baroclinic ﬂows (Figure 5.5). For the barotropic element, lines of constant p are

parallel to lines of constant ρ, which implies that the resultant pressure forces

pass through the center of mass of the element. For the baroclinic element, the

Figure 5.5 Mechanism of vorticity generation in baroclinic ﬂow, showing that the net pressure force does

not pass through the center of mass G. The radially inward arrows indicate pressure forces on an element.

148 Vorticity Dynamics

lines of constant p and ρ are not parallel. The net pressure force does not pass

through the center of mass, and the resulting torque changes the vorticity and

circulation.

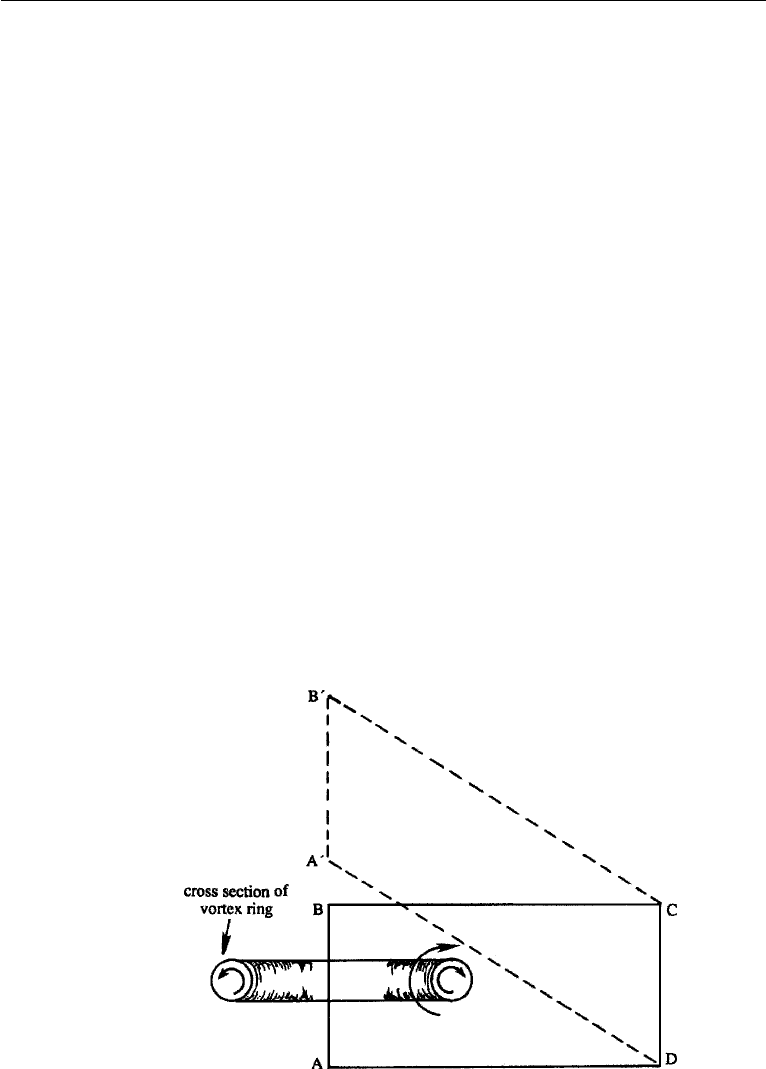
As an example of the generation of vorticity in a baroclinic ﬂow, consider a

gas at rest in a gravitational ﬁeld. Let the gas be heated locally, say by chemical

action (such as explosion of a bomb) or by a simple heater (Figure 5.6). The

gas expands and rises upward. The ﬂow is baroclinic because density here is

also a function of temperature. A doughnut-shaped ring-vortex (similar to the

smoke ring from a cigarette) forms and rises upward. (In a bomb explosion, a

mushroom-shaped cloud occupies the central hole of such a ring.) Consider a

closed ﬂuid circuit ABCD when the gas is at rest; the circulation around it is

then zero. If the region near AB is heated, the circuit assumes the new location



CD after an interval of time; circulation around it is nonzero because

•

dx along A



is nonzero. The circulation around a material circuit has

therefore changed, solely due to the baroclinicity of the ﬂow. This is one of

the reasons why geophysical ﬂows, which are dominated by baroclinicity,

are full of vorticity. It should be noted that no restriction is placed on the

compressibility of the ﬂuid, and Kelvin’s theorem is valid for incompressible

as well as compressible ﬂuids.

(4) Nonrotating frame: Motion observed with respect to a rotating frame of ref-

erence can develop vorticity and circulation by mechanisms not considered in

our demonstration of Kelvin’s theorem. Effects of a rotating frame of reference

are considered in Section 7.

Under the four restrictions mentioned in the foregoing, Kelvin’s theorem essentially

states that irrotational ﬂows remain irrotational at all times.

Figure 5.6 Local heating of a gas, illustrating vorticity generation on baroclinic ﬂow.

5. Vorticity Equation in a Nonrotating Frame 149

Helmholtz Vortex Theorems

Under the same four restrictions, Helmholtz proved the following theorems on vortex

motion:

(1) Vortex lines move with the ﬂuid.

(2) Strength of a vortex tube, that is the circulation, is constant along its length.

(3) A vortex tube cannot end within the ﬂuid. It must either end at a solid boundary

or form a closed loop (a “vortex ring”).

(4) Strength of a vortex tube remains constant in time.

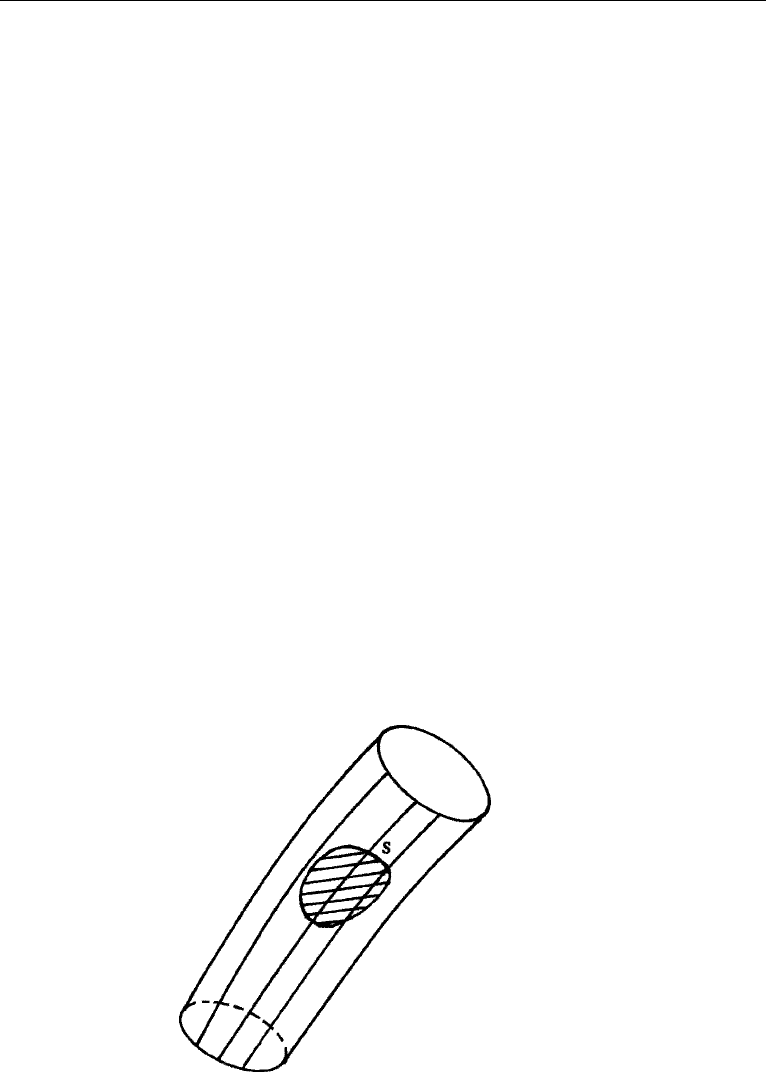
Here, we shall prove only the ﬁrst theorem, which essentially says that ﬂuid

particles that at any time are part of a vortex line always belong to the same vortex line.

To prove this result, consider an area S, bounded by a curve, lying on the surface of a

vortex tube without embracing it (Figure 5.7). As the vorticity vectors are everywhere

lying on the area element S, it follows that the circulation around the edge of S is

zero. After an interval of time, the same ﬂuid particles form a new surface, say S



According to Kelvin’s theorem, the circulation around S



must also be zero. As this is

true for any S, the component of vorticity normal to every element of S



must vanish,

demonstrating that S



must lie on the surface of the vortex tube. Thus, vortex tubes

move with the ﬂuid. Applying this result to an inﬁnitesimally thin vortex tube, we get

the Helmholtz vortex theorem that vortex lines move with the ﬂuid. A different proof

may be found in Sommerfeld (Mechanics of Deformable Bodies, pp. 130–132).

5. Vorticity Equation in a Nonrotating Frame

An equation governing the vorticity in a ﬁxed frame of reference is derived in this

section. The ﬂuid density is assumed to be constant, so that the ﬂow is barotropic.

Viscous effects are retained. Effects of nonbarotropic behavior and a rotating frame

Figure 5.7 Proof of Helmholtz’s vortex theorem.

150 Vorticity Dynamics

of reference are considered in the following section. The derivation given here uses

vector notation, so that we have to use several vector identities, including those for

triple products of vectors. Readers not willing to accept the use of such vector identities

can omit this section and move on to the next one, where the algebra is worked out

in tensor notation without using such identities.

Vorticity is deﬁned as

ω ≡ ∇ × u.

Because the divergence of a curl vanishes, vorticity for any ﬂow must satisfy

∇

•

ω = 0. (5.10)

An equation for rate of change of vorticity is obtained by taking the curl of the equation

of motion. We shall see that pressure and gravity are eliminated during this operation.

In symbolic form, we want to perform the operation

∇ ×



∂u

∂t

+ u

•

∇u =−

∇p + ∇ + ν∇



, (5.11)

where



is the body force potential. Using the vector identity

•

∇u = (∇ × u) × u +

∇(u

•

u) = ω × u +

∇q

and noting that the curl of a gradient vanishes, (5.11) gives

∂ω

∂t

+ ∇ × (ω × u) = ν∇

ω, (5.12)

where we have also used the identity ∇ ×∇

u =∇

(∇ ×u) in rewriting the viscous

term. The second term in equation (5.12) can be written as

∇ × (ω × u) = (u

•

∇)ω − (ω

•

∇)u,

where we have used the vector identity

∇ × (A × B) = A∇

•

B + (B

•

∇)A − B∇

•

A − (A

•

∇)B,

and that ∇

•

u = 0 and ∇

•

ω = 0. Equation (5.12) then becomes

Dω

= (ω

•

∇)u + ν∇

ω. (5.13)

This is the equation governing rate of change of vorticity in a ﬂuid with constant

ρ and conservative body forces. The term ν∇

ω represents the rate of change of ω

due to diffusion of vorticity in the same way that ν∇

u represents acceleration due

to diffusion of momentum. The term (ω

•

∇)u represents rate of change of vorticity

due to stretching and tilting of vortex lines. This important mechanism of vorticity

6. Velocity Induced by a Vortex Filament: Law ofBiot and Savart 151

generation is discussed further near the end of Section 7, to which the reader can

proceed if the rest of that section is not of interest. Note that pressure and gravity

terms do not appear in the vorticity equation, as these forces act through the center

of mass of an element and therefore generate no torque.

6. Velocity Induced by a Vortex Filament: Law of

Biot and Savart

It is often useful to be able to calculate the velocity induced by a vortex ﬁlament with

arbitrary orientation in space. This result is used in thin airfoil theory. We shall derive

the velocity induced by a vortex ﬁlament for a constant density ﬂow. (What actually

is required is a solenoidal velocity ﬁeld.) We start with the deﬁnition of vorticity,

ω ≡∇×u. Take the curl of this equation to obtain

∇×ω =∇×(∇×u) =∇(∇

•

u) −∇

We shall asume that mass conservation can be written as ∇

•

u = 0, (for example, if

ρ = const) and solve the vector Poisson equation for u in terms of ω. The Poisson

equation in the form ∇

φ =−ρ(r)/ε leads to the solution expressed as φ(r) =

(4πε)

−1





ρ(r



)|r − r



−1



where the integration is over all of V



) space.

Using this form for each component of vorticity, we obtain for u,

u = (4π)

−1





(∇



× ω)|r − r



−1



(5.14)

We take V



to be a small cylinder wrapped around the vortex line C through the point



. See Figure 5.8. Equation (5.14) can be rewritten in general as

u = (4π)

−1





{∇



×[ω/|r − r



|]−[∇



|r − r



−1

]×ω}dV



(5.15)

We use the divergence theorem on the ﬁrst integral in the form



(∇×F)dV =



A=∂V

dA × F. Then (5.15) becomes

u = (4π)

−1







=∂V



×ω/|r −r







(∇



|r −r



|) ×ω/|r −r





(5.16)

Now shrink V



and A



= ∂V



to surround the vortex line segment in the neighborhood

of r



. On the two end faces of A



, dA



||ω so dA



× ω = 0. Since, ∇

•

ω = 0, ω

is constant along a vortex line, so





sides



× ω = (





sides



) × ω = 0 and





sides



= 0 because the generatrix of A



sides

is a closed curve. For the second

integral, dV



= dA



•

dl, where dA



is an element of end face area and dl is arc length

along the vortex line. Now, by Stokes’ theorem,



end

•





C=∂A



•

ds = ,

where  is the circulation around the vortex line C and ds is an element of arc