Cohen I.M., Kundu P.K. Fluid Mechanics

Подождите немного. Документ загружается.

122 Conservation Laws

the momentum Bernoulli equation, both heat conduction and viscous stresses may

be neglected. This latter form from the energy equation becomes very useful for

high-speed gas ﬂows to show the interplay between kinetic energy and internal energy

or enthalpy or temperature along a streamline.

17. Applications of Bernoulli’s Equation

Application of Bernoulli’s equation will now be illustrated for some simple ﬂows.

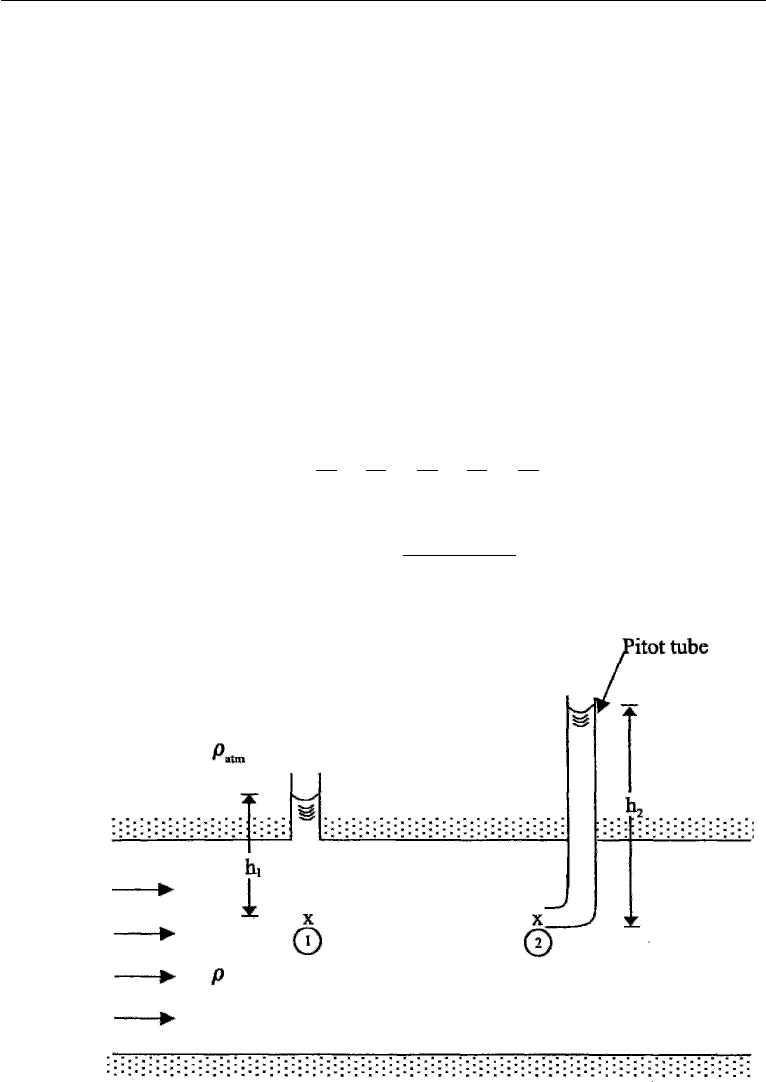
Pitot Tube

Consider ﬁrst a simple device to measure the local velocity in a ﬂuid stream by

inserting a narrow bent tube (Figure 4.19). This is called a pitot tube, after the French

mathematician Henri Pitot (1695–1771), who used a bent glass tube to measure the

velocity of the river Seine. Consider two points 1 and 2 at the same level, point 1 being

away from the tube and point 2 being immediately in front of the open end where the

ﬂuid velocity is zero. Friction is negligible along a streamline through 1 and 2, so that

Bernoulli’s equation (4.78) gives

from which the velocity is found to be



2(p

− p

)/ρ.

Figure 4.19 Pitot tube for measuring velocity in a duct.

17. Applications of Bernoulli’s Equation 123

Pressures at the two points are found from the hydrostatic balance

= ρgh

and p

= ρgh

so that the velocity can be found from



2g(h

− h

Because it is assumed that the ﬂuid density is very much greater than that of the

atmosphere to which the tubes are exposed, the pressures at the tops of the two ﬂuid

columns are assumed to be the same. They will actually differ by ρ

atm

g(h

− h

Use of the hydrostatic approximation above station 1 is valid when the streamlines

are straight and parallel between station 1 and the upper wall. In working out this

problem, the ﬂuid density also has been taken to be a constant.

The pressure p

measured by a pitot tube is called “stagnation pressure,” which

is larger than the local static pressure. Even when there is no pitot tube to measure

the stagnation pressure, it is customary to refer to the local value of the quantity

(p + ρu

/2) as the local stagnation pressure, deﬁned as the pressure that would be

reached if the local ﬂow is imagined to slow down to zero velocity frictionlessly. The

quantity ρu

/2 is sometimes called the dynamic pressure; stagnation pressure is the

sum of static and dynamic pressures.

Oriﬁce in a Tank

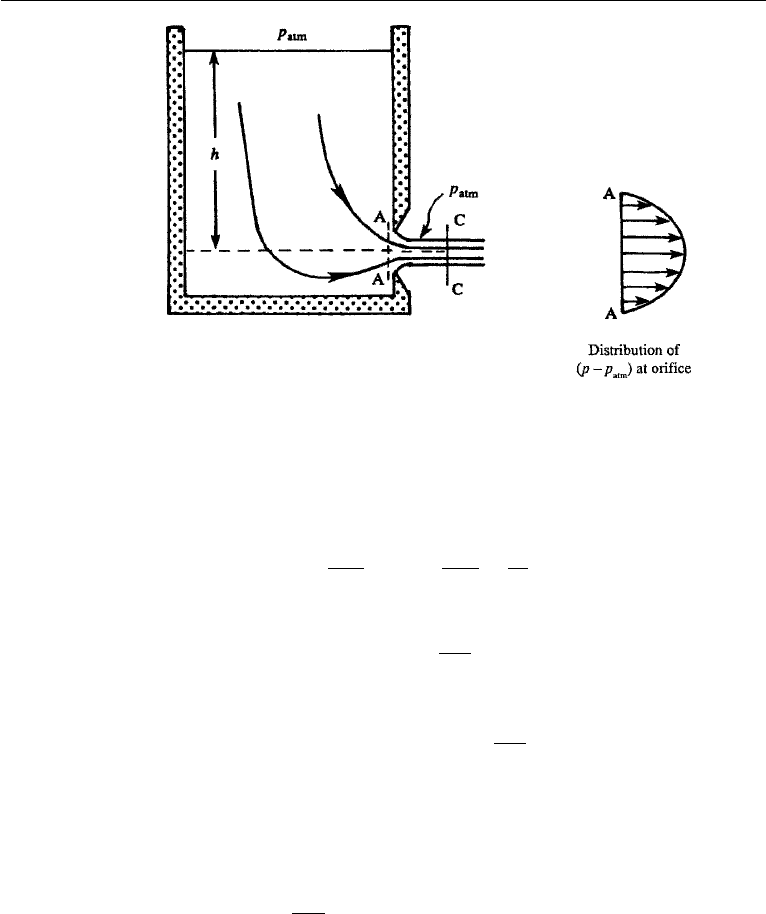
As another application of Bernoulli’s equation, consider the ﬂow through an oriﬁce

or opening in a tank (Figure 4.20). The ﬂow is slightly unsteady due to lowering of

the water level in the tank, but this effect is small if the tank area is large as compared

to the oriﬁce area. Viscous effects are negligible everywhere away from the walls of

the tank. All streamlines can be traced back to the free surface in the tank, where they

have the same value of the Bernoulli constant B = q

/2 +p/ρ + gz. It follows that

the ﬂow is irrotational, and B is constant throughout the ﬂow.

We want to apply Bernoulli’s equation between a point at the free surface in

the tank and a point in the jet. However, the conditions right at the opening (section

A in Figure 4.20) are not simple because the pressure is not uniform across the jet.

Although pressure has the atmospheric value everywhere on the free surface of the jet

(neglecting small surface tension effects), it is not equal to the atmospheric pressure

inside the jet at this section. The streamlines at the oriﬁce are curved, which requires

that pressure must vary across the width of the jet in order to balance the centrifugal

force. The pressure distribution across the oriﬁce (section A) is shown in Figure 4.20.

However, the streamlines in the jet become parallel at a short distance away from the

oriﬁce (section C in Figure 4.20), where the jet area is smaller than the oriﬁce area.

The pressure across section C is uniform and equal to the atmospheric value because

it has that value at the surface of the jet.

124 Conservation Laws

Figure 4.20 Flow through a sharp-edged oriﬁce. Pressure has the atmospheric value everywhere across

section CC; its distribution across oriﬁce AA is indicated.

Application of Bernoulli’s equation between a point on the free surface in the

tank and a point at C gives

atm

+ gh =

atm

from which the jet velocity is found as

u =



2gh,

which simply states that the loss of potential energy equals the gain of kinetic energy.

The mass ﬂow rate is

˙m = ρA

u = ρA



2gh,

where A

is the area of the jet at C. For oriﬁces having a sharp edge, A

has been

found to be ≈62% of the oriﬁce area.

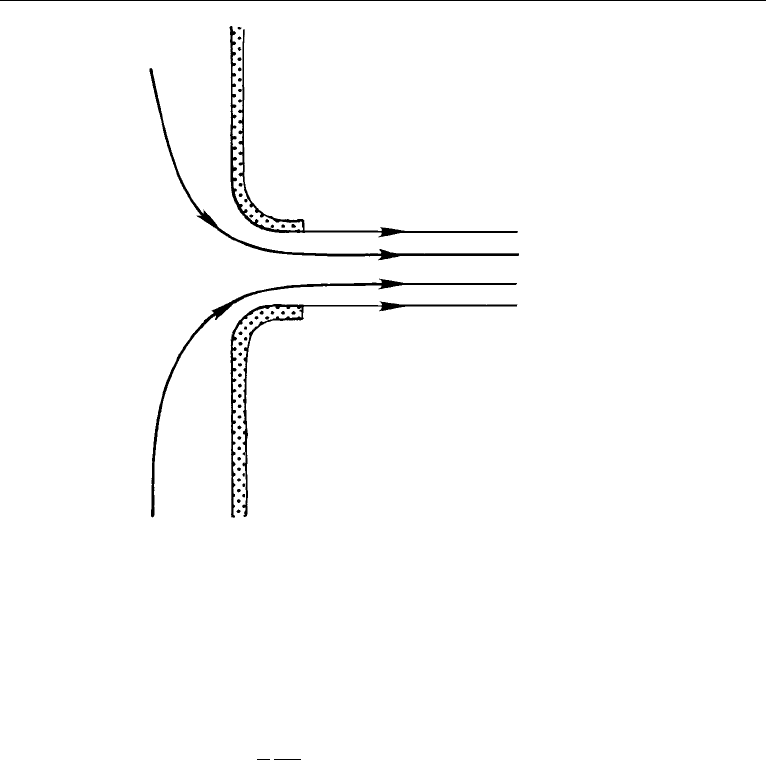
If the oriﬁce happens to have a well-rounded opening (Figure 4.21), then the jet

does not contract. The streamlines right at the exit are then parallel, and the pressure

at the exit is uniform and equal to the atmospheric pressure. Consequently the mass

ﬂow rate is simply ρA

√

2gh, where A equals the oriﬁce area.

18. Boussinesq Approximation

For ﬂows satisfying certain conditions, Boussinesq in 1903 suggested that the density

changes in the ﬂuid can be neglected except in the gravity term where ρ is multiplied

by g. This approximation also treats the other properties of the ﬂuid (such as µ, k, C

)

as constants. A formal justiﬁcation, and the conditions under which the Boussinesq

approximation holds, is given in Spiegel and Veronis (1960). Here we shall discuss the

18. Boussinesq Approximation 125

Figure 4.21 Flow through a rounded oriﬁce.

basis of the approximation in a somewhat intuitive manner and examine the resulting

simpliﬁcations of the equations of motion.

Continuity Equation

The Boussinesq approximation replaces the continuity equation

Dρ

+ ∇

•

u = 0, (4.83)

by the incompressible form

∇

•

u = 0. (4.84)

However, this does not mean that the density is regarded as constant along the direction

of motion, but simply that the magnitude of ρ

−1

(Dρ/Dt ) is small in comparison to

the magnitudes of the velocity gradients in ∇

•

u. We can immediately think of several

situations where the density variations cannot be neglected as such. The ﬁrst situation

is a steady ﬂow with large Mach numbers (deﬁned as U/c, where U is a typical

measure of the ﬂow speed and c is the speed of sound in the medium). At large Mach

numbers the compressibility effects are large, because the large pressure changes

cause large density changes. It is shown in Chapter 16 that compressibility effects

are negligible in ﬂows in which the Mach number is <0.3. A typical value of c for

126 Conservation Laws

air at ordinary temperatures is 350 m/s, so that the assumption is good for speeds

<100 m/s. For water c = 1470 m/s, but the speeds normally achievable in liquids

are much smaller than this value and therefore the incompressibility assumption is

very good in liquids.

A second situation in which the compressibility effects are important is unsteady

ﬂows. The waves would propagate at inﬁnite speed if the density variations are

neglected.

A third situation in which the compressibility effects are important occurs when

the vertical scale of the ﬂow is so large that the hydrostatic pressure variations cause

large changes in density. In a hydrostatic ﬁeld the vertical scale in which the density

changes become important is of order c

/g ∼ 10 km for air. (This length agrees with

the e-folding height RT /g of an “isothermal atmosphere,” because c

= γRT; see

Chapter 1, Section 10.) The Boussinesq approximation therefore requires that the

vertical scale of the ﬂow be L  c

/g.

In the three situations mentioned the medium is regarded as “compressible,” in

which the density depends strongly on pressure. Now suppose the compressibility

effects are small, so that the density changes are caused by temperature changes

alone, as in a thermal convection problem. In this case the Boussinesq approximation

applies when the temperature variations in the ﬂow are small. Assume that ρ changes

with T according to

δρ

=−αδT,

where α =−ρ

−1

(∂ρ/∂T )

is the thermal expansion coefﬁcient. For a perfect gas

α = 1/T ∼ 3 × 10

−3

−1

and for typical liquids α ∼ 5 × 10

−4

−1

. With a tem-

perature difference in the ﬂuid of 10

◦

C, the variation of density can be only a few

percent at most. It turns out that ρ

−1

(Dρ/Dt ) can also be no larger than a few

percent of the velocity gradients in ∇

•

u. To see this, assume that the ﬂow ﬁeld is

characterized by a length scale L, a velocity scale U , and a temperature scale δT .

By this we mean that the velocity varies by U and the temperature varies by δT ,in

a distance of order L. The ratio of the magnitudes of the two terms in the continuity

equation is

(1/ρ)(Dρ/Dt)

∇

•

∼

(1/ρ)u(∂ρ/∂x)

∂u/∂x

∼

(U/ρ)(δρ/L)

U/L

δρ

= αδT  1,

which allows us to replace continuity equation (4.83) by its incompressible

form (4.84).

Momentum Equation

Because of the incompressible continuity equation ∇

•

u = 0, the stress tensor is

given by equation (4.41). From equation (4.45), the equation of motion is then

=−∇p + ρg + µ∇

u. (4.85)

18. Boussinesq Approximation 127

Consider a hypothetical static reference state in which the density is ρ

everywhere and

the pressure is p

(z), so that ∇p

= ρ

g. Subtracting this state from equation (4.85)

and writing p = p

+ p



and ρ = ρ

+ ρ



, we obtain

=−∇p



+ ρ



g + µ∇

u. (4.86)

Dividing by ρ

, we obtain



1 +





=−

∇p



g + ν∇

where ν = µ/ρ

. The ratio ρ



/ρ

appears in both the inertia and the buoyancy terms.

For small values of ρ



/ρ

, the density variations generate only a small correction to

the inertia term and can be neglected. However, the buoyancy term ρ



g/ρ

is very

important and cannot be neglected. For example, it is these density variations that

drive the convective motion when a layer of ﬂuid is heated. The magnitude of ρ



g/ρ

is therefore of the same order as the vertical acceleration ∂w/∂t or the viscous term

ν∇

w. We conclude that the density variations are negligible the momentum equation,

except when ρ is multiplied by g.

Heat Equation

From equation (4.66), the thermal energy equation is

=−∇

•

q − p(∇

•

u) + φ. (4.87)

Although the continuity equation is approximately ∇

•

u = 0, an important point is

that the volume expansion term p(∇

•

u) is not negligible compared to other dominant

terms of equation (4.87); only for incompressible liquids is p(∇

•

u) negligible in

equation (4.87). We have

−p∇

•

u =

Dρ





∂ρ

∂T



=−pα

Assuming a perfect gas, for which p = ρRT , C

− C

= R and α = 1/T , the

foregoing estimate becomes

−p∇

•

u =−ρRT α

=−ρ(C

− C

)

Equation (4.87) then becomes

ρC

=−∇

•

q + φ, (4.88)

where we used e = C

T for a perfect gas. Note that we would have gotten C

(instead of C

) on the left-hand side of equation (4.88) if we had dropped ∇

•

u in

equation (4.87).

128 Conservation Laws

Now we show that the heating due to viscous dissipation of energy is negli-

gible under the restrictions underlying the Boussinesq approximation. Comparing

the magnitudes of viscous heating with the left-hand side of equation (4.88), we

obtain

ρC

(DT /Dt )

∼

2µe

ρC

(∂T /∂x

)

∼

µU

UδT/L

δT L

In typical situations this is extremely small (∼ 10

−7

). Neglecting φ, and assuming

Fourier’s law of heat conduction

q =−k∇T,

the heat equation (4.88) ﬁnally reduces to (if k = const.)

= κ∇

where κ ≡ k/ρC

is the thermal diffusivity.

Summary: The Boussinesq approximation applies if the Mach number of the

ﬂow is small, propagation of sound or shock waves is not considered, the ver-

tical scale of the ﬂow is not too large, and the temperature differences in the

ﬂuid are small. Then the density can be treated as a constant in both the con-

tinuity and the momentum equations, except in the gravity term. Properties of

the ﬂuid such as µ, k, and C

are also assumed constant in this approximation.

Omitting Coriolis forces, the set of equations corresponding to the Boussinesq

approximation is

∇

•

u = 0

=−

∂p

∂x

+ ν∇

=−

∂p

∂y

+ ν∇

=−

∂p

∂z

−

ρg

+ ν∇

= κ∇

ρ = ρ

[1 − α(T − T

)],

(4.89)

where the z-axis is taken upward. The constant ρ

is a reference density correspond-

ing to a reference temperature T

, which can be taken to be the mean temperature

in the ﬂow or the temperature at a boundary. Applications of the Boussinesq set

can be found in several places throughout the book, for example, in the problems of

wave propagation in a density-stratiﬁed medium, thermal instability, turbulence in a

stratiﬁed medium, and geophysical ﬂuid dynamics.

19. Boundary Conditions 129

19. Boundary Conditions

The differential equations we have derived for the conservation laws are subject to

boundary conditions in order to properly formulate any problem. Speciﬁcally, the

Navier-Stokes equations are of a form that requires the velocity vector to be given on

all surfaces bounding the ﬂow domain.

If we are solving for an external ﬂow, that is, a ﬂow over some body, we must

specify the velocity vector and the thermodynamic state on a closed distant surface.

On a solid boundary or at the interface between two immiscible liquids, conditions

may be derived from the three basic conservation laws as follows.

In Figure 4.22, a “pillbox” is drawn through the interface surface separating

medium 1 (ﬂuid) from medium 2 (solid or liquid immiscible with ﬂuid 1). Here dA

and dA

are elements of the end face areas in medium 1 and medium 2, respectively,

locally tangent to the interface, and separated from each other by a distance l.Now

apply the conservation laws to the volume deﬁned by the pillbox. Next, let l → 0,

keeping A

and A

in the different media. As l → 0, all volume integrals → 0 and

the integral over the side area, which is proportional to l, tends to zero as well. Deﬁne

a unit vector n, normal to the interface at the pillbox and pointed into medium 1.

Mass conservation gives ρ

· n = ρ

· n at each point on the interface as the

end face area becomes small. (Here we assume that the coordinates are ﬁxed to the

interface, that is, the interface is at rest. Later in this section we show the modiﬁcations

necessary when the interface is moving.)

If medium 2 is a solid, then u

= 0 there. If medium 1 and medium 2 are immis-

cible liquids, no mass ﬂows across the boundary surface. In either case, u

· n = 0

on the boundary. The same procedure applied to the integral form of the momentum

equation (4.16) gives the result that the force/area on the surface, n

is continuous

across the interface if surface tension is neglected. If surface tension is included, a

jump in pressure in the direction normal to the interface must be added; see Chapter 1,

Section 6 and the discussion later in this section.

Applying the integral form of energy conservation (4.64) to a pillbox of inﬁnites-

imal height l gives the result n

is continuous across the interface, or explicity,

(∂T

/∂n) = k

(∂T

/∂n) at the interface surface. The heat ﬂux must be continuous

at the interface; it cannot store heat.

Two more boundary conditions are required to completely specify a problem

and these are not consequences of any conservation law. These boundary conditions

are: no slip of a viscous ﬂuid is permitted at a solid boundary v

· t = 0; and no

Figure 4.22 Interface between two media; evaluation of boundary conditions.

130 Conservation Laws

temperature jump is permitted at the boundary T

= T

. Here t is a unit vector

tangent to the boundary.

Known violations of the no-slip boundary condition occur for superﬂuid helium

at or below 2.17

◦

K, which has an immeasurable small (essentially zero) viscosity. On

the other hand, the appearance of slip is created when water or water-based ﬂuids ﬂow

over ﬁnely textured “superhydrophobic” (strongly water repellent) coated surfaces.

This is described by Gogte et al. (2005). Surface textures must be much smaller than

the capillary length for water and were typically about 10µm . The ﬂuid did not slip

on the protrusions but did not penetrate the valleys because of the surface tension,

giving the appearance of slip. Both slip and temperature jump are known to occur

in highly rareﬁed gases, where the mean distances between intermolecular collisions

become of the order of the length scales of interest in the problem. The details are

closely related to the manner of gas-surface interaction of momentum and energy.

A recent review was given by McCormick (2005).

Boundary condition at a moving, deforming surface

Consider a surface in space that may be moving or deforming in some arbitrary way.

Examples may be ﬂexible solid boundaries, the interface between two immiscible

liquids, or a moving shock wave, as described in Chapter 16. The ﬁrst two examples

do not permit mass ﬂow across the interface, whereas the third does. Such a sur-

face can be deﬁned and its motion described in inertial coordinates by the equation

f(x, y, z, t) = 0. We often must treat problems in which boundary conditions must

be satisﬁed on such a moving, deforming interface. Let the velocity of a point that

remains on the surface be u

. An observer that remains on the surface always sees

f = 0, so for that observer,

df/dt = ∂f/∂t + u

•

∇f = 0onf = 0. (4.90)

A ﬂuid particle has velocity u. If no ﬂuid ﬂows across f = 0, then u

•

∇f =

•

∇f =−∂f/∂t. Thus the condition that there be no mass ﬂow across the surface

becomes,

∂f/∂t +u

•

∇f ≡ Df/Dt = 0onf = 0. (4.91)

If there is mass ﬂow across the surface, it is proportional to the relative velocity

between the ﬂuid and the surface, (u

)

= u

•

n − u

•

n, where n =∇f/|∇f |.

)

= u

•

∇f/|∇f |+[1/|∇f |][∂f/∂t]=[1/|∇f |]Df /D t . (4.92)

Thus the mass ﬂow rate across the surface (per unit surface area) is represented by

[ρ/|∇f |]Df/Dt on f = 0. (4.93)

Again, if no mass ﬂows across the surface, the requirement is Df/Dt = 0onf = 0.

Surface tension revisited: generalized discussion

As we discussed in Section 1.6 (p. 8), attractive intermolecular forces dominate

in a liquid, whereas in a gas repulsive forces are larger. However, as a liquid-gas

19. Boundary Conditions 131

phase boundary is approached from the liquid side, these attractive forces are not

felt equally because there are many fewer liquid phase molecules near the phase

boundary. Thus there tends to be an unbalanced attraction to the interior of the

liquid of the molecules on the phase boundary. This is called “surface tension”

and its manifestation is a pressure increment across a curved interface. A some-

what more detailed description is provided in texts on physicochemical hydrody-

namics. Two excellent sources are Probstein (1994, Chapter 10) and Levich (1962,

Chapter VII).

H. Lamb, Hydrodynamics (6

Edition, p. 456) writes, “Since the condition of

stable equilibrium is that the free energy be a minimum, the surface tends to contract

as much as is consistent with the other conditions of the problem.” Thus we are led

to introduce the Helmoltz free energy (per unit mass) via

F = e − TS, (4.94)

where the notation is consistent with that used in Section 1.8. If the free energy

is a minimum, then the system is in a state of stable equilibrium. F is called the

thermodynamic potential at constant volume [E. Fermi, T hermodynamics, p. 80].

For a reversible, isothermal change, the work done on the system is the gain in total

free energy F ,

dF = de − TdS − SdT, (4.95)

where the last term is zero for an isothermal change. Then, from (1.18), dF =−pdv =

work done on system. (These relations suggest that surface tension decreases with

increasing temperature.)

For an interface of area = A, separating two media of densities ρ

and ρ

, with

volumes V

and V

, respectively, and with a surface tension coefﬁcient σ (correspond-

ing to free energy per unit area), the total (Helmholtz) free energy of the system can

be written as

F = ρ

+ ρ

+ Aσ. (4.96)

If σ>0, then the two media (ﬂuids) are immiscible; on the other hand, if σ<0,

corresponding to surface compression, then the two ﬂuids mix freely. In the following,

we shall assume that σ = const. Flows driven by surface tension gradients are called

Marangoni ﬂows and are not discussed here. Our discussion will follow that given by

G. K. Batchelor, An Introduction to Fluid Dynamics, pp. 61ff.

We wish to determine the shape of a boundary between two stationary ﬂuids

compatible with mechanical equilibrium. Let the equation of the interface surface be

given by f (x,y,z) = 0 = z − ζ(x, y). Align the coordinates so that ζ(0, 0) = 0,

∂ζ /∂x|

0,0

= 0, ∂ζ /∂y|

0,0

= 0. See Figure 4.23. A normal to this surface is obtained

by forming the gradient, n =∇[z − ζ(x, y)]=k − i∂ζ /∂x − j∂ζ /∂y. The (x, y, z)

components of n are (−∂ζ/∂x,−∂ζ/∂y,1). Now the tensile forces on the bounding