Cohen I.M., Kundu P.K. Fluid Mechanics
Подождите немного. Документ загружается.

132 Conservation Laws
dr
z
0
x
y
surface z 2 (x, y) 5 0
Figure 4.23 Geometry of equilibrium interface with surface tension.
line of the surface are obtained from the line integral
= σ
dr × n
= σ
(i dx + j dy + k dz) × (k − i∂ζ /∂x − j∂ζ/∂y)
= σ
[−k(∂ζ /∂y)dx − jdx + k(∂ζ /∂x)dy + idy − j(∂ζ /∂x)dz + i(∂ζ /∂y)dz].
This integral is carried out over a contour C, which bounds the area A. Let that contour
Cbeinaz = const. plane so that dz = 0 on C. Then note that
(idy − jdx) =−k ×
(idx + jdy) =−k ×
dr = 0.
Then the tensile force acting on the bounding line C of the surface A
= kσ
[−(∂ζ /∂y)dx + (∂ζ /∂x)dy].
Now use Stokes’ theorem in the form
C=∂A
F
•
dr =
A
(∇×F)
•
dA, where here F =−(∂ζ /∂y)i + (∂ζ /∂x)j. Then
∇×F = (∂F
y
/∂x − ∂F
x
/∂y)k = (∂
2
ζ/∂x
2
+ ∂
2
ζ/∂y
2
)k, and
σ
C=∂A
[(−∂ζ/∂y)dx + (∂ζ /∂x)dy]=σ
A
(∂
2
ζ/∂x
2
+ ∂
2
ζ/∂y
2
)dA
z
. (4.97)
We had expanded in a small neighborhood of the origin so the force per surface
area is the last integrand = σ(∂
2
ζ/∂x
2
+ ∂
2
ζ/∂y
2
)
0,0
, and this is interpreted as a
pressure difference across the surface. The curvature of the surface in the y = 0 plane
=[∂
2
ζ/∂x
2
][1 +(∂ζ /∂x)
2
]
−3/2
. Since this is evaluated at (0,0) where ∂ζ /∂x = 0,

19. Boundary Conditions 133
the curvature reduces to ∂
2
ζ/∂x
2
≡ 1/R
1
(defining R
1
). Similarly, the curvature in
the x = 0 plane at (0,0) is ∂
2
ζ/∂y
2
≡ 1/R
2
(defining R
2
). Thus we say
p = σ(1/R
1
+ 1/R
2
), (4.98)
where the pressure is greater on the side with the center of curvature of the interface.
Batchelor (loc. cit., p. 64) writes “An unbounded surface with a constant sum of the
principal curvatures is spherical, and this must be the equilibrium shape of the surface.
This result also follows from the fact that in a state of (stable) equilibrium the energy
of the surface must be a minimum consistent with a given value of the volume of the
drop or bubble, and the sphere is the shape which has the least surface area for a given
volume.” The original source of this analysis is Lord Rayleigh (J. W. Strutt), “On the
Theory of Surface Forces,” Phil. Mag. (Ser. 5), Vol. 30, pp. 285–298, 456–475 (1890).
For an air bubble in water, gravity is an important factor for bubbles of millimeter
size, as we shall see here. The hydrostatic pressure for a liquid is obtained from
p
L
+ ρgz = const., where z is measured positively upwards from the free surface
and g is downwards. Thus for a gas bubble beneath the free surface,
p
G
= p
L
+ σ(1/R
1
+ 1/R
2
) = const. − ρgz + σ(1/R
1
+ 1/R
2
).
Gravity and surface tension are of the same order in effect over a length scale
(σ/ρg)
1/2
. For an air bubble in water at 288
◦
K, this scale =[7.35 × 10
−2
N/m/
(9.81 m/s
2
× 10
3
kg/m
3
)]
1/2
= 2.74 ×10
−3
m.
Example 4.3. Calculation of the shape of the free surface of a liquid adjoining an
infinite vertical plane wall. With reference to Figure 4.24, as defined above, 1/R
1
=
[∂
2
ζ/∂x
2
][1 + (∂ζ /∂x)
2
]
−3/2
= 0, and 1/R
2
=[∂
2
ζ/∂y
2
][1 + (∂ζ /∂y)
2
]
−3/2
.
At the free surface, ρgζ − σ/R
2
= const. As y →∞, ζ → 0, and R
2
→∞,so
const. = 0. Then ρgζ/σ −ζ
/(1 + ζ
2
)
3/2
= 0.
Multiply by the integrating factor ζ
and integrate. We obtain (ρg/2σ)ζ
2
+(1 +
ζ
2
)
−1/2
= C. Evaluate C as y →∞, ζ → 0, ζ
→ 0. Then C = 1. We look at
y = 0, z = ζ = h to find h. The slope at the wall, ζ
= tan(θ + π/2) =−cot θ.
Then 1 + ζ
2
= 1 +cot
2
θ = csc
2
θ . Thus we now have (ρg/2σ)h
2
= 1 −1/ csc θ
Gas
interface z 5 (x, y)
Liquid
h
Z
Solid
y
u
Figure 4.24 Free surface of a liquid adjoining a vertical plane wall.

134 Conservation Laws
= 1−sin θ, so that h
2
= (2σ/ρg)(1−sin θ). Finally we seek to integrate to obtain the
shape of the interface. Squaring and rearranging the result above, the differential equa-
tion we must solve may be written as 1+(dζ /dy)
2
=[1−(ρg/2σ)ζ
2
]
−2
. Solving for
the slope and taking the negative square root (since the slope is negative for positive y),
dζ /dy =−{1 −[1 −(ρg/2σ)ζ
2
]
2
}
1/2
[1 − (ρg/2σ)ζ
2
]
−1
.
Define σ/ρg = d
2
, ζ/d = η. Rewriting the equation in terms of y/d and η, and
separating variables,
2(1 −η
2
/2)η
−1
(4 − η
2
)
−1/2
dη = d(y/d).
The integrand on the left is simplified by partial fractions and the constant of integra-
tion is evaluated at y = 0 when η = h/d. Finally
cosh
−1
(2d/ζ) − (4 − ζ
2
/d
2
)
1/2
− cosh
−1
(2d/h) + (4 − h
2
/d
2
)
1/2
= y/d
gives the shape of the interface in terms of y(ζ).
Analysis of surface tension effects results in the appearance of additional dimen-
sionless parameters in which surface tension is compared with other effects such
as viscous stresses, body forces such as gravity, and inertia. These are defined in
Chapter 8.
Exercises
1. Let a one-dimensional velocity field be u = u(x, t), with v = 0 and
w = 0. The density varies as ρ = ρ
0
(2 −cos ωt). Find an expression for u(x, t)
if u(0,t) = U .
2. In Section 3 we derived the continuity equation (4.8) by starting from the inte-
gral form of the law of conservation of mass for a fixed region. Derive equation (4.8)
by starting from an integral form for a material volume. [Hint: Formulate the principle
for a material volume and then use equation (4.5).]
3. Consider conservation of angular momentum derived from the angular
momentum principle by the word statement: Rate of increase of angular momentum
in volume V = net influx of angular momentum across the bounding surface A of V
+ torques due to surface forces + torques due to body forces. Here, the only torques
are due to the same forces that appear in (linear) momentum conservation. The possi-
bilities for body torques and couple stresses have been neglected. The torques due to
the surface forces are manipulated as follows. The torque about a point O due to the
element of surface force τ
mk
dA
m
is
ij k
x
j
τ
mk
dA
m
, where x is the position vector
from O to the element dA. Using Gauss’ theorem, we write this as a volume integral,
V
ε
ij k
∂
∂x
m
(x
j
τ
mk
)dV = ε
ij k
V
∂x
j
∂x
m
τ
mk
+ x
j
∂τ
mk
∂x
m
dV
= ε
ij k
V
τ
jk
+ x
j
∂τ
mk
∂x
m
dV,

Exercises 135
where we have used ∂x
j
/∂x
m
= δ
jm
. The second term is
V
x ×∇·τ dV and
combines with the remaining terms in the conservation of angular momentum to give
V
x×(Linear Momentum: equation (4.17)) dV =
V
ij k
τ
jk
dV. Since the left-hand
side = 0 for any volume V , we conclude that ε
ij k
τ
kj
= 0, which leads to τ
ij
= τ
ji
.
4. Near the end of Section 7 we derived the equation of motion (4.15) by starting
from an integral form for a material volume. Derive equation (4.15) by starting from
the integral statement for a fixed region, given by equation (4.22).
5. Verify the validity of the second form of the viscous dissipation given in
equation (4.60). [Hint: Complete the square and use δ
ij
δ
ij
= δ
ii
= 3.]
6. A rectangular tank is placed on wheels and is given a constant horizontal
acceleration a. Show that, at steady state, the angle made by the free surface with the
horizontal is given by tan θ = a/g.
7. A jet of water with a diameter of 8 cm and a speed of 25 m/s impinges normally
on a large stationary flat plate. Find the force required to hold the plate stationary.
Compare the average pressure on the plate with the stagnation pressure if the plate is
20 times the area of the jet.
8. Show that the thrust developed by a stationary rocket motor is F = ρAU
2
+
A(p − p
atm
), where p
atm
is the atmospheric pressure, and p, ρ, A, and U are,
respectively, the pressure, density, area, and velocity of the fluid at the nozzle exit.
9. Consider the propeller of an airplane moving with a velocity U
1
.Takea
reference frame in which the air is moving and the propeller [disk] is stationary. Then
the effect of the propeller is to accelerate the fluid from the upstream value U
1
to
the downstream value U
2
>U
1
. Assuming incompressibility, show that the thrust
developed by the propeller is given by
F =
ρA
2
(U
2
2
− U
2
1
),
where A is the projected area of the propeller and ρ is the density (assumed constant).
Show also that the velocity of the fluid at the plane of the propeller is the average value
U = (U
1
+U
2
)/2. [Hint: The flow can be idealized by a pressure jump, of magnitude
p = F/A right at the location of the propeller. Also apply Bernoulli’s equation
between a section far upstream and a section immediately upstream of the propeller.
Also apply the Bernoulli equation between a section immediately downstream of the
propeller and a section far downstream. This will show that p = ρ(U
2
2
− U
2
1
)/2.]
10. A hemispherical vessel of radius R has a small rounded orifice of area A at
the bottom. Show that the time required to lower the level from h
1
to h
2
is given by
t =
2π
A
√
2g
2
3
R
h
3/2
1
− h
3/2
2
−
1
5
h
5/2
1
− h
5/2
2
.
11. Consider an incompressible planar Couette flow, which is the flow between
two parallel plates separated by a distance b. The upper plate is moving parallel to
136 Conservation Laws
itself at speed U , and the lower plate is stationary. Let the x-axis lie on the lower plate.
All flow fields are independent of x. Show that the pressure distribution is hydrostatic
and that the solution of the Navier–Stokes equation is
u(y) =
Uy
b
.
Write the expressions for the stress and strain rate tensors, and show that the viscous
dissipation per unit volume is φ = µU
2
/b
2
.
Take a rectangular control volume for which the two horizontal surfaces coincide
with the walls and the two vertical surfaces are perpendicular to the flow. Evaluate
every term of energy equation (4.63) for this control volume, and show that the balance
is between the viscous dissipation and the work done in moving the upper surface.
12. The components of a mass flow vector ρu are ρu = 4x
2
y, ρv = xyz,
ρw = yz
2
. Compute the net outflow through the closed surface formed by the planes
x = 0, x = 1, y = 0, y = 1, z = 0, z = 1.
(a) Integrate over the closed surface.
(b) Integrate over the volume bounded by that surface.
13. Prove that the velocity field given by u
r
= 0, u
θ
= k/(2πr) can have only
two possible values of the circulation. They are (a) = 0 for any path not enclosing
the origin, and (b) = k for any path enclosing the origin.
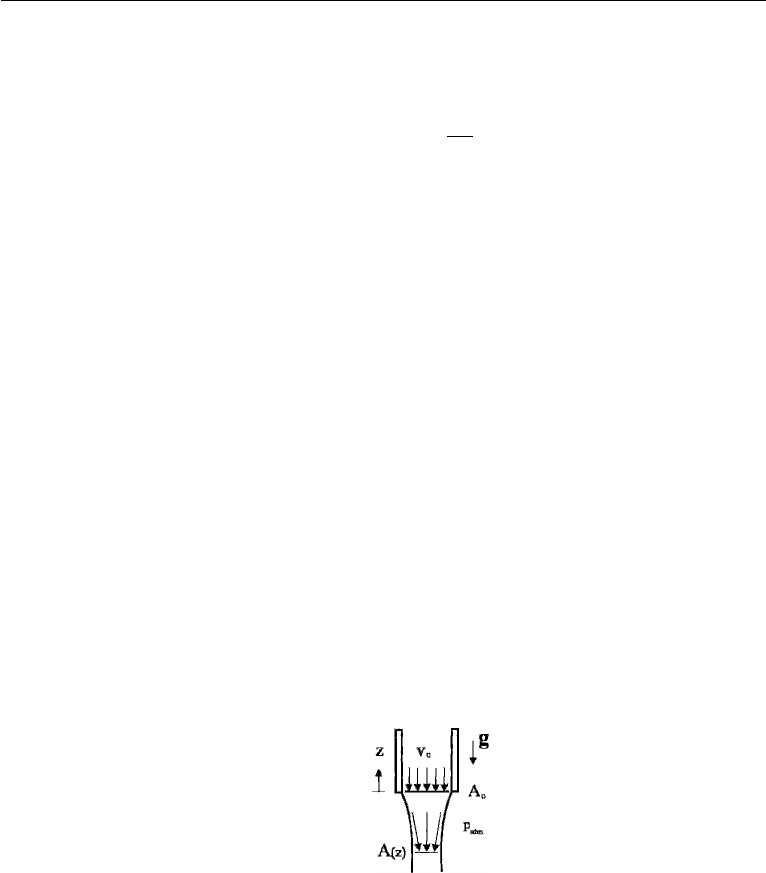
14. Water flows through a pipe in a gravitational field as shown in the accompa-
nying figure. Neglect the effects of viscosity and surface tension. Solve the appropriate
conservation equations for the variation of the cross-sectional area of the fluid column
A(z) after the water has left the pipe at z = 0. The velocity of the fluid at z = 0is
uniform at v
0
and the cross-sectional area is A
0
.
15. Redo the solution for the “orifice in a tank” problem allowing for the fact
that in Fig. 4.20, h = h(t). How long does the tank take to empty?
Literature Cited
Aris, R. (1962). Vectors, Tensors, and the Basic Equations of Fluid Mechanics, Englewood Cliffs, NJ:
Prentice-Hall. (The basic equations of motion and the various forms of the Reynolds transport theorem
are derived and discussed.)
Batchelor, G. K. (1967). An Introduction to Fluid Dynamics, London: Cambridge University Press. (This
contains an excellent and authoritative treatment of the basic equations.)

Supplemental Reading 137
Fermi, E. (1956). Thermodynamics, New York: Dover Publications, Inc.
Gogte, S. P. Vorobieff, R. Truesdell, A. Mammoli, F. van Swol, P. Shah, and C. J. Brinker (2005). “Effective
slip on textured superhydrophobic surfaces.” Phys. Fluids 17: 051701.
Lamb, H. (1945). Hydrodynamics, Sixth Edition, New York: Dover Publications, Inc.
Levich, V. G. (1962). Physicochemical Hydrodynamics, Second Edition, Englewood Cliffs, NJ:
Prentice-Hall, Chapter VII.
Lord Rayleigh (J. W. Strutt) (1890). “On the Theory of Surface Forces.” Phil. Mag. (Ser. 5), 30: 285–298,
456–475.
McCormick, N. J. (2005). “Gas-surface accomodation coefficients from viscous slip and temperature jump
coefficients.” Phys. Fluids 17: 107104.
Holton, J. R. (1979). An Introduction to Dynamic Meteorology, New York: Academic Press.
Pedlosky, J. (1987). Geophysical Fluid Dynamics, New York: Springer-Verlag.
Probstein, R. F. (1994). Physicochemical Hydrodynamics, Second Edition, New York: John Wiley & Sons,
Chapter 19.
Spiegel, E. A. and G. Veronis (1960). On the Boussinesq approximation for a compressible fluid. Astro-
physical Journal 131: 442–447.
Stommel H. M. and D. W. Moore (1989) An Introduction to the Coriolis Force. New York: Columbia
University Press.
Truesdell, C. A. (1952). Stokes’ principle of viscosity. Journal of Rational Mechanics and Analysis 1:
228–231.
Supplemental Reading
Chandrasekhar, S. (1961). Hydrodynamic and Hydromagnetic Stability, London: Oxford University Press.
(This is a good source to learn the basic equations in a brief and simple way.)
Dussan V., E. B. (1979). “On the Spreading of Liquids on Solid Surfaces: Static and Dynamic Contact
Lines.” Annual Rev. of Fluid Mech. 11, 371–400.
Levich, V. G. and V. S. Krylov (1969). “Surface Tension Driven Phenomena.” Annual Rev. of Fluid Mech.
1, 293–316.
This page intentionally left blank

Chapter 5
Vorticity Dynamics
1. Introduction ..................... 139
2. Vortex Lines and Vortex
Tubes ........................... 140
3. Role of Viscosity in Rotational and
Irrotational Vortices ............. 141
Solid-Body Rotation ............. 141
Irrotational Vortex ............... 142
Discussion....................... 143
4. Kelvin’s Circulation Theorem .... 144
Discussion of Kelvin’s Theorem . . 147
Helmholtz Vortex Theorems...... 149
5. Vorticity Equation in a Nonrotating
Frame ........................... 149
6. Velocity Induced by a Vortex Filament:
Law of Biot and Savart .......... 151
7. Vorticity Equation in a Rotating
Frame ........................... 152
Meaning of (ω
•
∇)u ............. 155
Meaning of 2(
•
∇)u............ 156
8. Interaction of Vortices ............ 157
9. Vortex Sheet ..................... 161
Exercises ........................ 161
Literature Cited ................. 163
Supplemental Reading ........... 163
1. Introduction
Motion in circular streamlines is called vortex motion. The presence of closed stream-
lines does not necessarily mean that the fluid particles are rotating about their own
centers, and we may have rotational as well as irrotational vortices depending on
whether the fluid particles have vorticity or not. The two basic vortex flows are the
solid-body rotation
u
θ
=
1
2
ωr, (5.1)
and the irrotational vortex
u
θ
=
2πr
. (5.2)
These are discussed in Chapter 3, Section 11, where also, the angular velocity in the
solid-body rotation was denoted by ω
0
= ω/2. Moreover, the vorticity of an element
is everywhere equal to ω for the solid-body rotation represented by equation (5.1), so
that the circulation around any contour is ω times the area enclosed by the contour.
139
©2010 Elsevier Inc. All rights reserved.
DOI: 10.1016/B978-0-12-381399-2.50005-8
140 Vorticity Dynamics
In contrast, the flow represented by equation (5.2) is irrotational everywhere except
at the origin, where the vorticity is infinite. All the vorticity of this flow is therefore
concentrated on a line coinciding with the vortex axis. Circulation around any circuit
not enclosing the origin is therefore zero, and that enclosing the origin is .An
irrotational vortex is therefore called a line vortex. Some aspects of the dynamics of
flows with vorticity are examined in this chapter.
2. Vortex Lines and Vortex Tubes
A vortex line is a curve in the fluid such that its tangent at any point gives the direction
of the local vorticity. A vortex line is therefore related to the vorticity vector the same
way a streamline is related to the velocity vector. If ω
x
, ω
y
, and ω
z
are the Cartesian
components of the vorticity vector ω, then the orientation of a vortex line satisfies the
equations
dx
ω
x
=
dy
ω
y
=
dz
ω
z
, (5.3)
which is analogous to equation (3.7) for a streamline. In an irrotational vortex, the
only vortex line in the flow field is the axis of the vortex. In a solid-body rotation, all
lines perpendicular to the plane of flow are vortex lines.
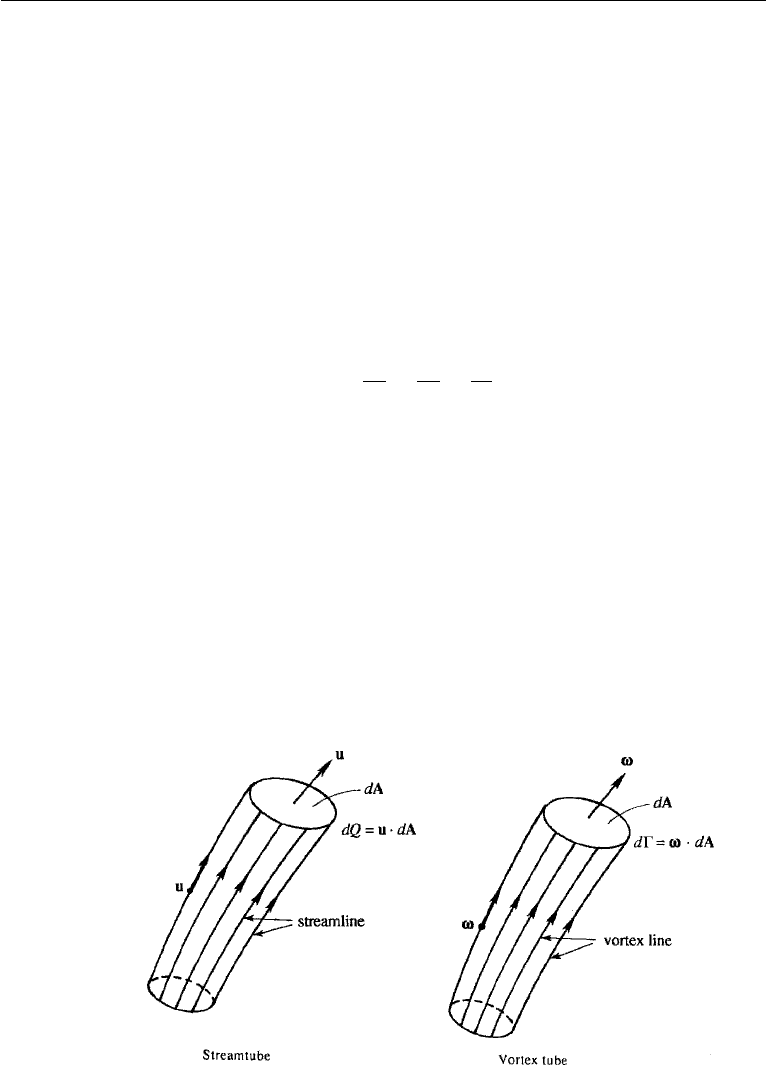
Vortex lines passing through any closed curve form a tubular surface, which is
called a vortex tube. Just as streamlines bound a streamtube, a group of vortex lines
bound a vortex tube (Figure 5.1). The circulation around a narrow vortex tube is
d = ω
•
dA, which is similar to the expression for the rate of flow dQ = u
•
dA
through a narrow streamtube. The strength of a vortex tube is defined as the circulation
around a closed circuit taken on the surface of the tube and embracing it just once.
From Stokes’ theorem it follows that the strength of a vortex tube is equal to the mean
vorticity times its cross-sectional area.
Figure 5.1 Analogy between streamtube and vortex tube.

3. Role of Viscosity in Rotational and Irrotational Vortices 141
3. Role of Viscosity in Rotational and Irrotational Vortices
The role of viscosity in the two basic types of vortex flows, namely the solid-body
rotation and the irrotational vortex, is examined in this section. Assuming incompress-
ible flow, we shall see that in one of these flows the viscous terms in the momentum
equation drop out, although the viscous stress and dissipation of energy are nonzero.
The two flows are examined separately in what follows.
Solid-Body Rotation
As discussed in Chapter 3, fluid elements in a solid-body rotation do not deform.
Because viscous stresses are proportional to deformation rate, they are zero in this
flow. This can be demonstrated by using the expression for viscous stress in polar
coordinates:
σ
rθ
= µ
1
r
∂u
r
∂θ
+ r
∂
∂r
u
θ
r
= 0,
where we have substituted u
θ
= ωr/2 and u
r
= 0. We can therefore apply the inviscid
Euler equations, which in polar coordinates simplify to
−ρ
u
2
θ
r
=−
∂p
∂r
0 =−
∂p
∂z
− ρg.
(5.4)
The pressure difference between two neighboring points is therefore
dp =
∂p
∂r
dr +
∂p
∂z
dz =
1
4
ρrω
2
dr − ρg dz,
where u
θ
= ωr/2 has been used. Integration between any two points 1 and 2 gives
p
2
− p
1
=
1
8
ρω
2
(r
2
2
− r
2
1
) − ρg(z
2
− z
1
). (5.5)
Surfaces of constant pressure are given by
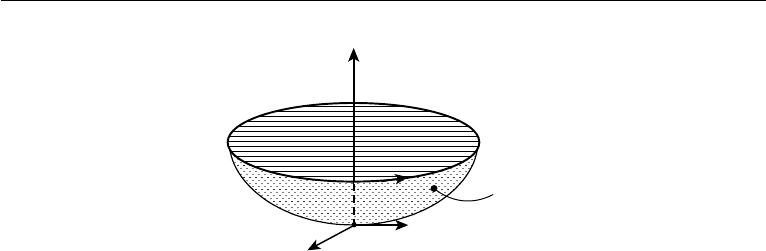
z
2
− z
1
=
1
8
(ω
2
/g)(r
2
2
− r
2
1
),
which are paraboloids of revolution (Figure 5.2).
The important point to note is that viscous stresses are absent in this flow. (The
viscous stresses, however, are important during the transient period of initiating the
motion, say by steadily rotating a tank containing a viscous fluid at rest.) In terms of
velocity, equation (5.5) can be written as
p
2
−
1
2
ρu
2
θ2
+ ρgz
2
= p
1
−
1
2
ρu
2
θ1
+ ρgz
1
,
