Coburn J.W., Herdlick J.D. College Algebra: Graphs and Models
Подождите немного. Документ загружается.


81. 82.
83. 84.
85. 86.
87.
88.
89. 90.
Use the discriminant to determine whether the
given equation has irrational, rational, repeated,
or nonreal roots. Also state whether the original
equation is factorable using integers, but do not
solve for x.
91. 92.
93. 94.
95. 96.
97. 98.
99. 100.
101. 102.
Solve the equations given. Simplify each result.
103. 104.
105. 106.
107. 108.
Solve each quadratic inequality by locating the
x-intercept(s) (if they exist), and noting the end-behavior
of the graph. Begin by writing the inequality in function
form as needed.
109.
110.
111.
112.
113.
114.
115. 116.
117. 118.
119. 120.
121.
122.
123.
124. f
1x2⫽ 9x
2
⫺ 6x ⫹ 1; f 1x26 0
r1x2⫽ 4x
2
⫹ 12x ⫹ 9; r1x26 0
t1x2⫽ x
2
⫺ 6x ⫹ 9; t1x2ⱖ 0
s1x2⫽ x
2
⫺ 8x ⫹ 16; s1x2ⱖ 0
4x
2
ⱖ 3x ⫹ 73x
2
ⱖ⫺2x ⫹ 5
x
2
⫺ 2 ⱕ 5xx
2
⫹ 3x ⱕ 6
x
2
ⱕ 137 ⱖ x
2
r1x2⫽⫺2x
2
⫺ 3x ⫹ 5; r1x27 0
q1x2⫽ 2x
2
⫺ 5x ⫺ 7; q1x26 0
p1x2⫽⫺x
2
⫹ 3x ⫹ 10; p1x2ⱕ 0
h1x2⫽ x
2
⫹ 4x ⫺ 5; h1x2ⱖ 0
g1x2⫽ x
2
⫺ 5x; g1x26 0
f
1x2⫽⫺x
2
⫹ 4x; f 1x27 0
4x ⫺ 3 ⫽ 5x
2
⫺2x
2
⫽⫺5x ⫹ 11
x
2
⫽⫺2x ⫺ 195x
2
⫹ 5 ⫽⫺5x
17 ⫹ 2x
2
⫽ 10x⫺6x ⫹ 2x
2
⫹ 5 ⫽ 0
9x
2
⫹ 4 ⫽ 12x4x
2
⫹ 12x ⫽⫺9
x
2
⫹ 4 ⫽⫺7x2x
2
⫹ 8 ⫽⫺9x
⫺5x
2
⫺ 3 ⫽ 2x⫺4x
2
⫹ 6x ⫺ 5 ⫽ 0
10x
2
⫺ 11x ⫺ 35 ⫽ 015x
2
⫺ x ⫺ 6 ⫽ 0
⫺10x ⫹ x
2
⫹ 41 ⫽ 0⫺4x ⫹ x
2
⫹ 13 ⫽ 0
2x
2
⫺ 5x ⫺ 3 ⫽ 0⫺3x
2
⫹ 2x ⫹ 1 ⫽ 0
5
9
x
2
⫺
16
15
x ⫽
3
2
2
7
p
2
⫺ 3 ⫽
8
21
p
⫺5.4n
2
⫹ 8.1n ⫹ 9 ⫽ 0
0.2a
2
⫹ 1.2a ⫹ 0.9 ⫽ 0
5
4
m
2
⫺
8
3
m ⫹
1
6
⫽ 0w
2
⫹
2
3
w ⫽
1
9
8x
2
⫺ 5x ⫺ 1 ⫽ 02p
2
⫺ 4p ⫹ 11 ⫽ 0
n
2
⫹ 4n ⫺ 8 ⫽ 02a
2
⫹ 5 ⫽ 3a 125.
126.
127. 128.
129. 130.
131. 132.
Solve each quadratic inequality using the interval test
method. Write your answer in interval notation when
possible.
133. 134.
135. 136.
137. 138.
139. 140.
141. 142.
143. 144.
Recall that for a square root expression to represent a
real number, the radicand must be greater than or equal
to zero. Applying this idea results in an inequality that
can be solved using the skills from this section.
Determine the domain of the following radical
functions.
145.
146.
147.
148.
149.
150.
Match the correct solution with the inequality and
graph given.
151.
a.
b.
c.
d.
e. none of these
152.
a.
b.
c.
d.
e. none of these
3⫺4, 14
1⫺4, 12
x 僆 1⫺q, ⫺44 ´ 31, q2
x 僆 1⫺q, ⫺42 ´ 11, q2
g1x2ⱖ 0
3⫺2, 14
1⫺2, 12
x 僆 1⫺q, ⫺24 ´ 31, q2
x 僆 1⫺q, ⫺22 ´ 11, q2
f
1x27 0
Y
1
⫽ 2x
2
⫺ 6x ⫹ 9
t1x2⫽ 2⫺x
2
⫹ 3x ⫺ 4
r1x2⫽ 26x ⫺ x
2
q1x2⫽ 2x
2
⫺ 5x
p1x2⫽ 225 ⫺ x
2
h1x2⫽ 2x
2
⫺ 25
⫺x
2
⫹ 6x ⫺ 9 ⱕ 0x
2
⫹ 14x ⫹ 49 ⱖ 0
⫺ax ⫹
1
8
b
2
7 0ax ⫺
3
5
b
2
6 0
1x ⫹ 3.22
2
ⱕ 0⫺1x ⫺ 2.92
2
ⱖ 0
⫺1x ⫺ 2.22
2
6 01x ⫹ 1.32
2
7 0
⫺3x
2
⫹ x ⫹ 4 ⱕ 02x
2
⫺ x ⫺ 6 ⱖ 0
1x ⫹ 221x ⫺ 526 01x ⫹ 321x ⫺ 126 0
5x
2
ⱖ 4x ⫺ 42x
2
ⱖ 6x ⫺ 9
⫺x
2
⫹ 3x 6 3x
2
⫺ 2x 7 ⫺5
x
2
6 ⫺4⫺x
2
7 2
h1x2⫽⫺x
2
⫹ 14x ⫺ 49; h1x26 0
g1x2⫽⫺x
2
⫹ 10x ⫺ 25; g1x26 0
310 CHAPTER 3 Quadratic Functions and Operations on Functions 3–30
College Algebra G&M—
5⫺5
⫺5
5
x
y
f(x)
5⫺5
⫺5
5
x
y
g(x)
cob19545_ch03_293-313.qxd 11/25/10 3:30 PM Page 310

153.
a.
b.
c. {3}
d. { }
e. none of these
x 僆 1⫺q, q2
x 僆 1⫺q, 32 ´ 13, q2
r1x2ⱕ 0 154.
a.
b.
c. {0}
d. { }
e. none of these
x 僆 1⫺q, q2
x 僆 1⫺q, 02 ´ 10, q2
s1x26 0
3–31 Section 3.2 Solving Quadratic Equations and Inequalities 311
College Algebra G&M—
8⫺2
⫺7
3
x
y
r(x)
5⫺5
⫺3
7
x
y
s(x)
䊳
WORKING WITH FORMULAS
155. Height of a projectile:
If an object is projected vertically upward from
ground level with no continuing source of propulsion,
the height of the object (in feet) is modeled by the
equation shown, where v is the initial velocity, and t is
the time in seconds. Use the quadratic formula to
solve for t in terms of v and h. (Hint: Set the equation
equal to zero and identify the coefficients as before.)
h ⴝⴚ16t
2
ⴙ vt 156. Surface area of a cylinder:
The surface area of a cylinder is given by the formula
shown, where h is the height and r is the radius of the
base. The equation can be considered a quadratic in
the variable r. Use the quadratic formula to solve for r
in terms of h and A. (Hint: Rewrite the equation in
standard form and identify the coefficients as before.)
A ⴝ 2r
2
ⴙ 2rh
䊳
APPLICATIONS
157. Height of a projectile: The height of an object
thrown upward from the roof of a building 408 ft
tall, with an initial velocity of 96 ft/sec, is given by
the equation where h
represents the height of the object after t seconds.
How long will it take the object to hit the ground?
Answer in exact form and decimal form rounded to
the nearest hundredth.
158. Height of a projectile: The height of an object
thrown upward from the floor of a canyon 106 ft
deep, with an initial velocity of 120 ft/sec, is given
by the equation where
h represents the height of the object after t seconds.
How long will it take the object to rise to the height
of the canyon wall ? Answer in exact form
and decimal form rounded to hundredths.
159. Cost, revenue, and
profit: The cost of
raw materials to
produce plastic
toys is given by the
cost equation
where x is the
number of toys in
hundreds. The total
income (revenue)
from the sale of
these toys is given
by (a) Determine the
profit equation (b) During
the Christmas season, the owners of the company
1profit ⫽ revenue ⫺ cost2.
R ⫽⫺x
2
⫹ 122x ⫺ 1965.
C ⫽ 2x ⫹ 35,
1h ⫽ 02
h ⫽⫺16t
2
⫹ 120t ⫺ 106,
h ⫽⫺16t
2
⫹ 96t ⫹ 408,
decide to manufacture and donate as many toys as
they can, without taking a loss (i.e., they break
even: profit or How many toys will they
produce for charity?
160. Cost, revenue, and profit: The cost to produce
bottled spring water is given by the cost equation
where x is the number of bottles in
thousands. The total revenue from the sale of these
bottles is given by the equation
(a) Determine the
profit equation (b) After
a bad flood contaminates the drinking water of a
nearby community, the owners decide to bottle and
donate as many bottles of water as they can,
without taking a loss (i.e., they break even: profit
or ). Approximately how many bottles will
they produce for the flood victims?
161. Height of an arrow: If an object is projected
vertically upward from ground level with no
continuing source of propulsion, its height (in feet)
is modeled by the equation where
v is the initial velocity and t is the time in seconds.
Use the quadratic formula to solve for t, given an
arrow is shot into the air with and
See Exercise 155.
162. Surface area of a cylinder: The surface area of a
cylinder is given by where h is
the height and r is the radius of the base. The
equation can be considered a quadratic in the
variable r. Use the quadratic formula to solve for
r, given and See
Exercise 156.
h ⫽ 35 cm.A ⫽ 4710 cm
2
A ⫽ 2r
2
⫹ 2rh,
h ⫽ 260 ft.
v ⫽ 144 ft/sec
h ⫽⫺16t
2
⫹ vt,
P ⫽ 0
1profit ⫽ revenue ⫺ cost2.
R ⫽⫺x
2
⫹ 326x ⫺ 18,463.
C ⫽ 16x ⫹ 63,
P ⫽ 02.
cob19545_ch03_293-313.qxd 8/10/10 6:09 PM Page 311

163. Tennis court dimensions: A
regulation tennis court for a
doubles match is laid out so that
its length is 6 ft more than two
times its width. The area of the
doubles court is What
is the length and width of the
doubles court?
164. Tennis court dimensions: A
regulation tennis court for a
singles match is laid out so that
its length is 3 ft less than three
times its width. The area of the
singles court is What is the length and
width of the singles court?
165. Cost, revenue, and profit: The revenue for a
manufacturer of microwave ovens is given by the
equation where revenue is in
thousands of dollars and x thousand ovens are
manufactured and sold. What is the minimum
number of microwave ovens that must be sold to
bring in a revenue of at least $900,000?
166. Cost, revenue, and profit: The revenue for a
manufacturer of computer printers is given by the
R ⫽ x140 ⫺
1
3
x2,
2106 ft
2
.
2808 ft
2
.
equation , where revenue is in
thousands of dollars and x thousand printers are
manufactured and sold. What is the minimum
number of printers that must be sold to bring in a
revenue of at least $440,000?
167. Cell phone subscribers: For the years 1995 to
2002, the number N of cellular phone subscribers
(in millions) can be modeled by the equation
where
represents the year 1995 [Source: Data from the
2005 Statistical Abstract of the United States, Table
1372, page 870]. If this trend continued, in what
year did the number of subscribers reach or surpass
3750 million?
168. U.S. international trade balance: For the years
1995 to 2003, the international trade balance B (in
millions of dollars) can be approximated
by the equation
where represents the year 1995 [Source:
Data from the 2005 Statistical Abstract of the
United States, Table 1278, page 799]. If this trend
continues, in what year will the trade balance reach
a deficit of $750 million dollars or more?
x ⫽ 0
B ⫽⫺3.1x
2
⫹ 4.5x ⫺ 19.9,
x ⫽ 0N ⫽ 17.4x
2
⫹ 36.1x ⫹ 83.3,
R ⫽ x130 ⫺ 0.4x2
312 CHAPTER 3 Quadratic Functions and Operations on Functions 3–32
College Algebra G&M—
Doubles
Singles
Exercises 163
and 164
䊳
EXTENDING THE CONCEPT
169. Using the discriminant: Each of the following
equations can easily be solved by factoring. Using
the discriminant, we can create factorable equations
with identical values for b and c, but where
For instance, and
can both be solved by
factoring. Find similar equations for the
quadratics given here. (Hint: The discriminant
must be a perfect square.)
a.
b.
c.
170. Using the discriminant: For what values of c will
the equation have
a. no real roots
b. one rational root
c. two real roots
d. two integer roots
9x
2
⫺ 12x ⫹ c ⫽ 0
x
2
⫺ x ⫺ 6 ⫽ 0
x
2
⫹ 5x ⫺ 14 ⫽ 0
x
2
⫹ 6x ⫺ 16 ⫽ 0
b
2
⫺ 4ac
1a ⫽ 12
4x
2
⫺ 3x ⫺ 10 ⫽ 0
x
2
⫺ 3x ⫺ 10 ⫽ 0
a ⫽ 1.
Complex polynomials: Many techniques applied to solve
polynomial equations with real coefficients can be
applied to solve polynomial equations with complex
coefficients. Here we apply the idea to carefully chosen
quadratic equations, as a more general application must
wait until a future course, when the square root of a
complex number is fully developed. Solve each equation
using the quadratic formula, noting that
171.
172.
173.
174.
175.
176. 0.5z
2
⫹ 14 ⫺ 3i2z ⫹ 1⫺9 ⫺ 12i2⫽ 0
0.5z
2
⫹ 17 ⫹ i2z ⫹ 16 ⫹ 7i2⫽ 0
2iz
2
⫺ 9z ⫹ 26i ⫽ 0
4iz
2
⫹ 5z ⫹ 6i ⫽ 0
z
2
⫺ 9iz ⫽⫺22
z
2
⫺ 3iz ⫽⫺10
1
i
ⴝⴚi.
cob19545_ch03_293-313.qxd 8/10/10 6:09 PM Page 312
3–33 Section 3.3 Quadratic Functions and Applications 313
College Algebra G&M—
䊳
MAINTAINING YOUR SKILLS
177. (R.3) State the formula for the perimeter and area
of each figure illustrated.
a. b.
c. d.
a
h
b
c
b
1
b
2
ch
r
L
W
178. (R.4) Factor and solve the following equations:
a.
b.
c.
179. (1.4) A total of 900 tickets were sold for a recent
concert and $25,000 was collected. If good seats
were $30 and cheap seats were $20, how many of
each type were sold?
180. (1.5) Solve for C: P ⫽ C ⫹ Ct.
x
3
⫹ 6x
2
⫺ 4x ⫺ 24 ⫽ 0
4x
2
⫺ 25 ⫽ 0
x
2
⫺ 5x ⫺ 36 ⫽ 0
3.3 Quadratic Functions and Applications
As our knowledge of functions grows, our ability to apply mathematics in new ways like-
wise grows. In this section, we’ll build on the foundation laid in Section 3.2 and previous
chapters, as we introduce additional tools used to apply quadratic functions effectively.
A. Graphing Quadratic Functions by Completing the Square
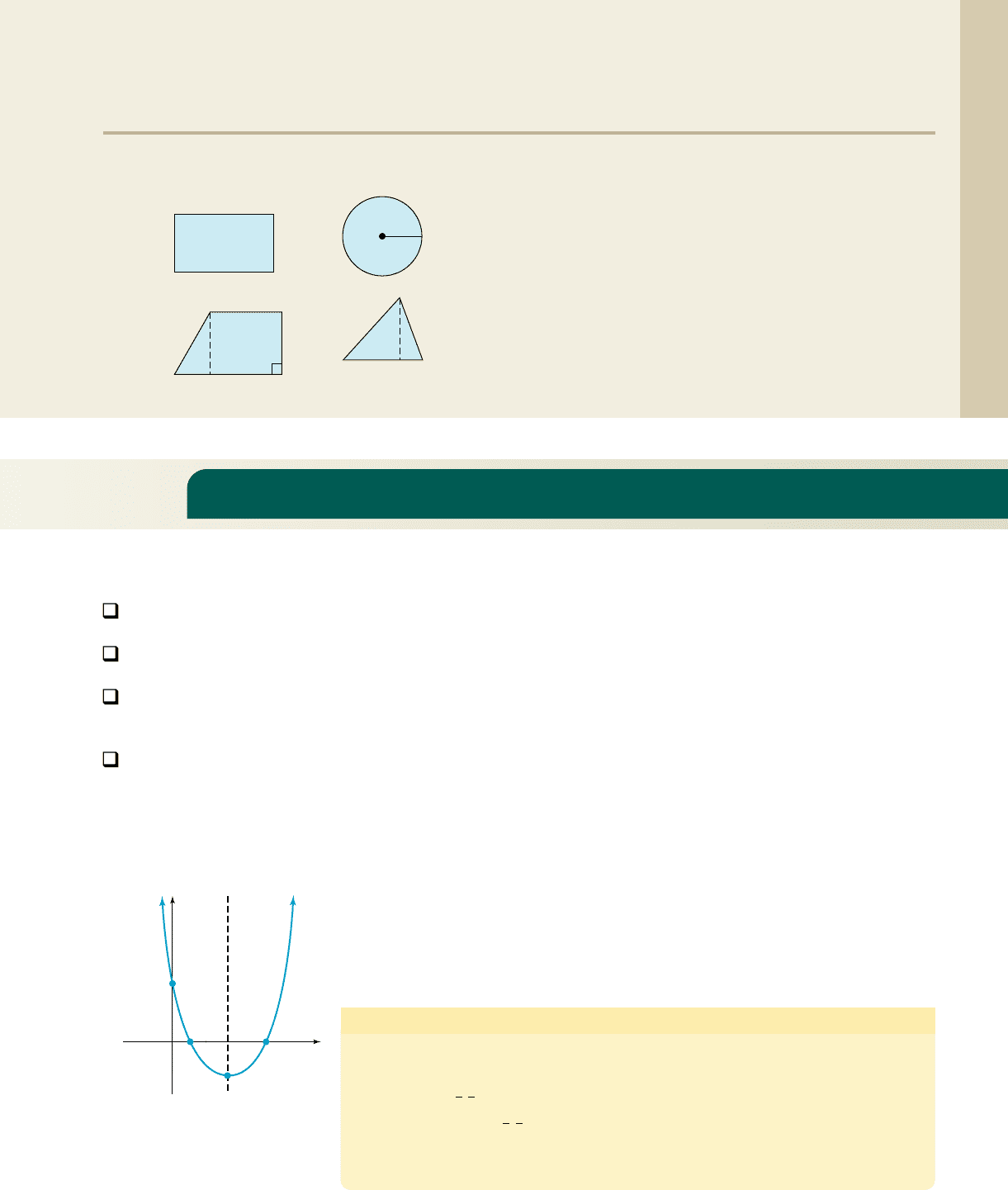
Our earlier work suggests the graph of any quadratic function will be a parabola.
Figure 3.40 provides a summary of the graph’s characteristic features. As pictured,
1. The parabola opens upward .
2. The vertex is at (h, k) and y = k is a global minimum.
3. The vertex is below the x-axis, so there are two x-intercepts.
4. The axis of symmetry contains the vertex, with equation .
5. The y-intercept is (0, c), since .
In Section 2.2, we graphed transformations of , using
Here, we’ll show that by completing the square, we can graph any quadratic function as
a transformation of this basic graph.
When completing the square on a quadratic equation (Section 3.2), we applied the
standard properties of equality to both sides of the equation. When completing the
square on a quadratic function, the process is altered slightly, so that we operate on
only one side.
The basic ideas are summarized here.
Graphing by Completing the Square
1. Group the variable terms apart from the constant c.
2. Factor out the leading coefficient a from this group.
3. Compute and add the result to the variable terms,
then subtract from c to maintain an equivalent expression.
4. Factor the grouped terms as a binomial square and combine constant terms.
5. Graph using transformations of .f
1x2⫽ x
2
a
#
3
1
2
1
b
a
24
2
3
1
2
1
b
a
24
2
f1x2ⴝ ax
2
ⴙ bx ⴙ c
y ⫽ a1x ⫾ h2
2
⫾ k.f 1x2⫽ x
2
f 102⫽ c
x ⫽ h
1y ⫽ ax
2
⫹ bx ⫹ c, a 7 02
LEARNING OBJECTIVES
In Section 3.3 you will see how we can:
A. Graph quadratic functions
by completing the square
B. Graph quadratic functions
using the vertex formula
C. Find the equation of a
quadratic function from
its graph
D. Solve applications
involving extreme values
Axis of
symmetry
End-
behavior
Vertex
(h, k)
x-intercepts
y-intercept
x
y
(x
2
, 0)
(x
1
, 0)
(0, c)
x h
Figure 3.40 f(x) ⫽ ax
2
⫹ bx ⫹ c
cob19545_ch03_293-313.qxd 8/10/10 6:10 PM Page 313
College Algebra G&M—
EXAMPLE 1
䊳
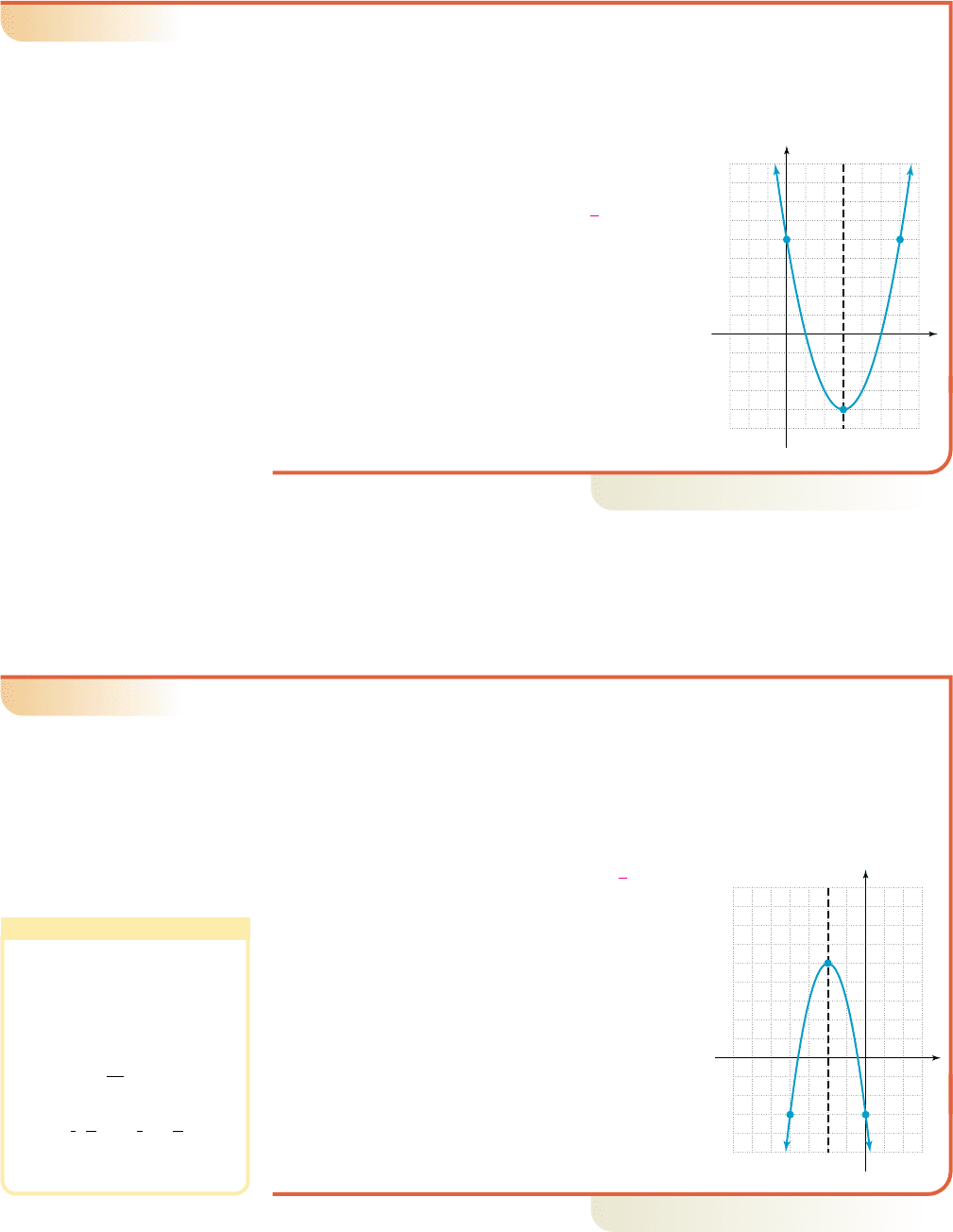
Graphing a Quadratic Function by Completing the Square
Given , complete the square to
rewrite g as a transformation of , then graph the function.
Solution
䊳
To begin we note the leading coefficient is .
given function
group variable terms
factor and simplify
The graph of g is the graph of f shifted 3 units right,
and 4 units down. The graph opens upward ( )
with the vertex at (3, ), and axis of symmetry
. From the original equation we find ,
giving a y-intercept of (0, 5). The point (6, 5) was
obtained using the symmetry of the graph. The graph
is shown in the figure.
Now try Exercises 7 through 10
䊳
Note that by adding 9 and simultaneously subtracting 9 (essentially adding “0”),
we changed only the form of the function, not its value. In other words, the resulting
expression is equivalent to the original. If the leading coefficient is not 1, we factor it
out from the variable terms, but take it into account when we add the constant needed
to maintain an equivalent expression (steps 2 and 3).
EXAMPLE 2
䊳
Graphing a Quadratic Function by Completing the Square
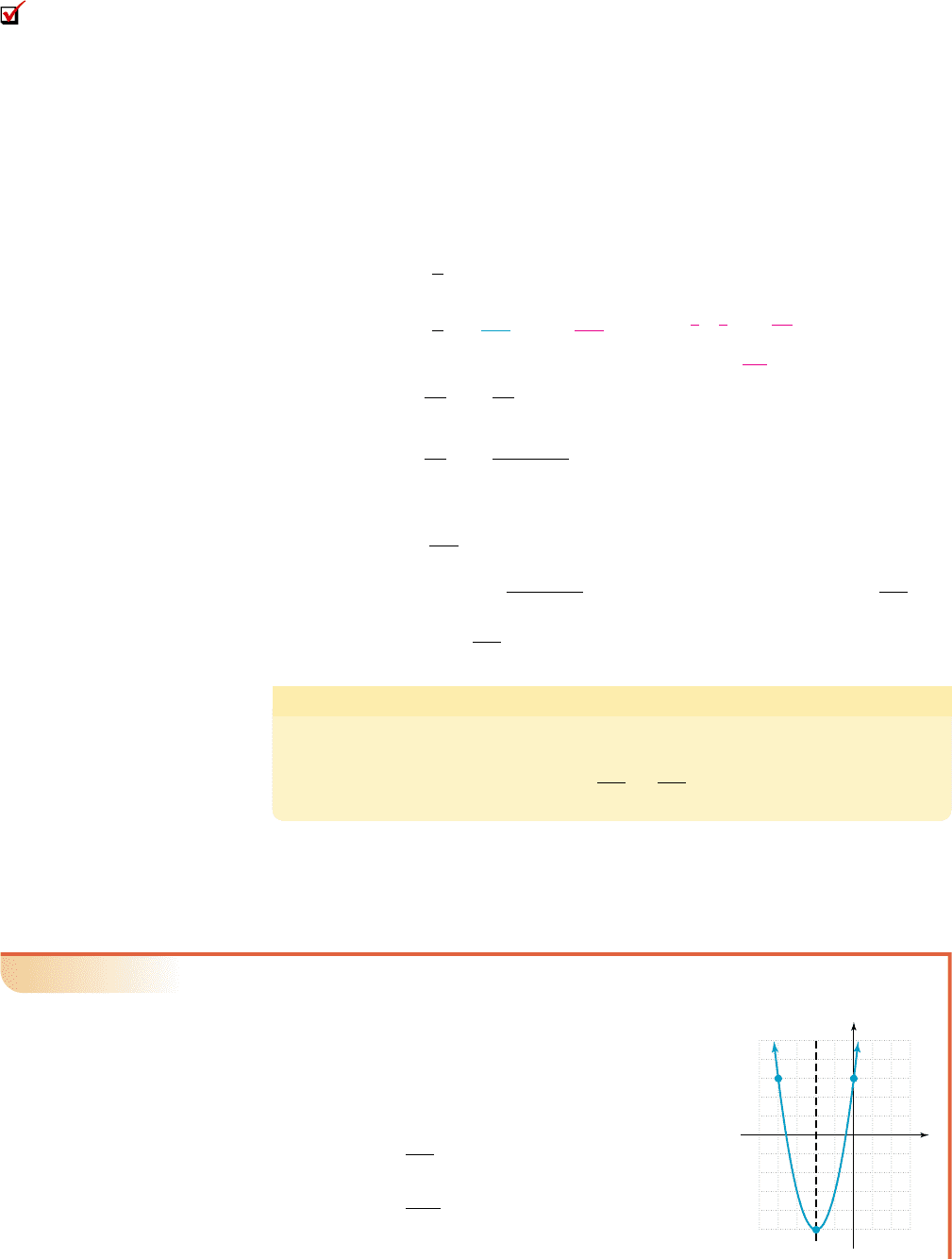
Given , complete the square to rewrite p as a transformation
of , then graph the function.
Solution
䊳
given function
group variable terms
factor out (notice sign change)
result
The graph of p is a parabola, shifted 2 units left,
stretched by a factor of 2, reflected across the x-axis
(opens downward), and shifted up 5 units. The
vertex is ( , 5), and the axis of symmetry is
. From the original function, the y-intercept
is (0, ). The point ( ) was obtained using
the symmetry of the graph. The graph is shown in
the figure.
Now try Exercises 11 through 20
䊳
4, 33
x 2
2
21x 22
2
5
21x 22
2
8 3
ca
1
2
b142d
2
4 21x
2
4x 42 182 3
a 2 21x
2
4x
___
23
12x
2
8x
___
23
p1x22x
2
8x 3
f
1x2 x
2
p1x22x
2
8x 3
g102 5x 3
4
a 7 0
1x 32
2
4
ca
1
2
b162d
2
9 11x
2
6x 92 9 5
11x
2
6x
___
2 5
g1x2 x
2
6x 5
a 1
f
1x2 x
2
g1x2 x
2
6x 5
(3, 4)
(6, 5)
(0, 5)
3
5
5
x
y
x 3
g(x)
⎤
⎪
⎬
⎪
⎦
subtract 9
adds 1
#
9 9
314 CHAPTER 3 Quadratic Functions and Operations on Functions 3–34
⎤
⎪
⎬
⎪
⎦
adds 2
#
4 8
subtract 8
(4, 3)
(2, 5)
(0, 3)
35
5
5
x
x 2
p(x)
y
factor trinomial,
simplify
WORTHY OF NOTE
In cases like ,
where the linear coefficient has no
integer factors of a, we factor out 3
and simultaneously divide the linear
coefficient by 3. This yields
and the process continues as
before: , and
so on. For more on this idea, see
Exercises 15 through 20.
31
1
2
21
10
3
24
2
1
5
3
2
2
25
9
h1x2 3 ax
2
10
3
x
____
b 5,
f 1x2 3x
2
10x 5
cob19545_ch03_314-328.qxd 8/10/10 8:14 PM Page 314
3–35 Section 3.3 Quadratic Functions and Applications 315
College Algebra G&M—
In Example 2, note that by adding 4 to the variable terms within parentheses,
we actually added to the value of the function. To adjust for this we
subtracted .
B. Graphing Quadratic Functions Using the Vertex Formula
When the process of completing the square is applied to , we ob-
tain a very useful result. Notice the close similarities to Example 2.
quadratic function
group variable terms apart from the constant
c
factor out
a
factor the trinomial, simplify
result
By comparing this result with previous transformations, we note the x-coordinate
of the vertex is (since the graph shifts horizontally “opposite the sign”). While
we could use the expression for k, we find it easier to substitute back
into the function: . The result is called the vertex formula.
Vertex Formula
For the quadratic function , the coordinates of the vertex are
Since all characteristic features of the graph (end-behavior, vertex, axis of sym-
metry, x-intercepts, and y-intercept) can now be determined using the original equa-
tion, we’ll rely on these features to sketch quadratic graphs, rather than having to
complete the square.
EXAMPLE 3
䊳
Graphing a Quadratic Function Using the Vertex Formula
Graph using the vertex formula
and other features of a quadratic graph.
Solution
䊳
The graph will open upward since .
The y-intercept is (0, 3).
The vertex formula gives
x
-coordinate of vertex
substitute 2 for
a
and 8 for
b
simplify 2
8
2122
h
b
2a
a 7 0
f
1x2 2x
2
8x 3
1h, k2 a
b
2a
, f a
b
2a
bb
f
1x2 ax
2
bx c
k f a
b
2a
b
b
2a
4ac b
2
4a
h
b
2a
a
ax
b
2a
b
2
4ac b
2
4a
a
ax
b
2a
b
2
b
2
4a
c
a
ax
2
b
a
x
b
2
4a
2
b a a
b
2
4a
2
b c
a
ax
2
b
a
x
___
b c
1ax
2
bx
___
2 c
f
1x2 ax
2
bx c
f
1x2 ax
2
bx c
8
2
#
4 8
A. You’ve just seen how
we can graph quadratic
functions by completing the
square
, add within group,
subtract a a
b
2
4a
2
b
ca
1
2
b a
b
a
bd
2
b
2
4a
2
(4, 3)
(2, 5)
(0, 3)
35
5
5
x
x 2
y
f(x)
cob19545_ch03_314-328.qxd 8/10/10 8:15 PM Page 315

Computing to find the y-coordinate of the vertex yields
substitute for
x
multiply
simplify
result
The vertex is . The graph is shown in the figure, with the point ( , 3)
obtained using symmetry.
Now try Exercises 21 through 32
䊳
C. Finding the Equation of a Quadratic Function from Its Graph
While most of our emphasis so far has centered on graphing quadratic functions, it
would be hard to overstate the importance of the reverse process—determining the
equation of the function from its graph (as in Section 2.2). This reverse process, which
began with our study of lines, will be a continuing theme each time we consider a
new function.
EXAMPLE 4
䊳
Finding the Equation of a Quadratic Function
The graph shown is a transformation of . What function defines this graph?
Solution
䊳
Compared to the graph of , the vertex has been shifted left 1 and up 2, so
the function will have the form . Since the graph opens
downward, we know a will be negative. As before, we select one additional point
on the graph and substitute to find the value of a. Using we obtain
transformation
substitute 1 for
x
and 0 for
F
(
x
)
simplify
subtract 2
solve for
a
The equation of this function is
Now try Exercises 33 through 38
䊳
D. Quadratic Functions and Extreme Values
If , the parabola opens upward, and the y-coordinate of the vertex is a global
minimum, the smallest value attained by the function anywhere in its domain. Con-
versely, if the parabola opens downward and the vertex yields a global maximum.
These greatest and least points are known as extreme values and have a number of
significant applications.
Note that when graphing technology is used in a real-world context, the focus on
the algebra involved is now shared with the context and meaning of the variables in-
volved. This analysis enables us to find an appropriate viewing window, and a better
interpretation of the results obtained.
a 6 0
a 7 0
F1x2
1
2
1x 12
2
2.
1
2
a
2 4a
0 4a 2
0 a
11 12
2
2
F1x2 a
1x 12
2
2
1x, y2S 11, 02
F1x2 a1x 12
2
2
f
1x2 x
2
f 1x2 x
2
412, 52
5
8 13
2142 16 3
2 f 122 2122
2
8122 3
f
122
316 CHAPTER 3 Quadratic Functions and Operations on Functions 3–36
College Algebra G&M—
B. You’ve just seen how
we can graph quadratic
functions using the vertex
formula
5
5
5
5
x
y
C. You’ve just seen how
we can find the equation of a
quadratic function from its
graph
WORTHY OF NOTE
It helps to remember that any point
(x, y) on the parabola can be used.
To verify this, try the calculation
again using .13, 02
cob19545_ch03_314-328.qxd 11/25/10 3:32 PM Page 316

3–37 Section 3.3 Quadratic Functions and Applications 317
College Algebra G&M—
EXAMPLE 5
䊳
Applying a Quadratic Model to Manufacturing
An airplane manufacturer can produce up to 15 planes per month. Suppose the
profit made from the sale of these planes is modeled by ,
where P(x) is the profit in hundred-thousands of dollars per month, and x is the
number of planes sold. Based on this model,
a. Find the y-intercept and explain what it means in this context.
b. How many planes should be made and sold to maximize profit?
c. What is the maximum profit?
Analytical Solution
䊳
a. , which means the manufacturer loses $300,000 each month if the
company produces no planes.
b. Since , we know the graph opens downward and has a maximum value.
To find the required number of sales needed to “maximize profit,” we use the
vertex formula with and :
vertex formula
substitute for
a
and 4 for
b
result
The result shows 10 planes should be sold each month for maximum profit.
c. Evaluating P(10) we find that a maximum profit of 17 “hundred-thousand
dollars” will be earned ($1,700,000).
Graphical Solution
䊳
a. Regardless of the solution method (analytical or graphical), the y-intercept will
be the constant term. Here indicates a loss of $300,000 if no planes
are made.
b. and c. After entering as Y
1
, we can use the (CALC)
4:maximum option to locate the extreme value. Before we do, we need to set
a window that will enable us to view and interpret the results. First, we know
that the solution must occur in QI, since both x and P(x) must be positive.
We’re told the manufacturer can make at most 15 planes per month, so it
seems reasonable to set and (to allow for a “frame”
around the window). Using and leaving for now
produces the graph shown in Figure 3.41. As the “top half” of the parabola is
missing, we increase the maximum y-value of our window to ,
yielding the graph in Figure 3.42. The sequence (CALC) 4:maximum
(and then naming the appropriate bounds) shows the vertex occurs at (10, 17)
(Figure 3.43), meaning a maximum profit of will
be earned when 10 planes are made and sold .
Now try Exercises 41 through 46
䊳
1x 102
17 $100,000 $1,700,000
2nd
Ymax 20
Ymax 10Ymin 0
Xmax 20Xmin 0
2nd
0.2x
2
4x 3
y 3
10
0.2
4
210.22
x
b
2a
b 4a 0.2
a 6 0
P1023
P1x20.2x
2
4x 3
20
10
0
0
20
20
0
0 20
20
0
0
Figure 3.42
Figure 3.43
Figure 3.41
cob19545_ch03_314-328.qxd 8/10/10 8:15 PM Page 317
318 CHAPTER 3 Quadratic Functions and Operations on Functions 3–38
College Algebra G&M—
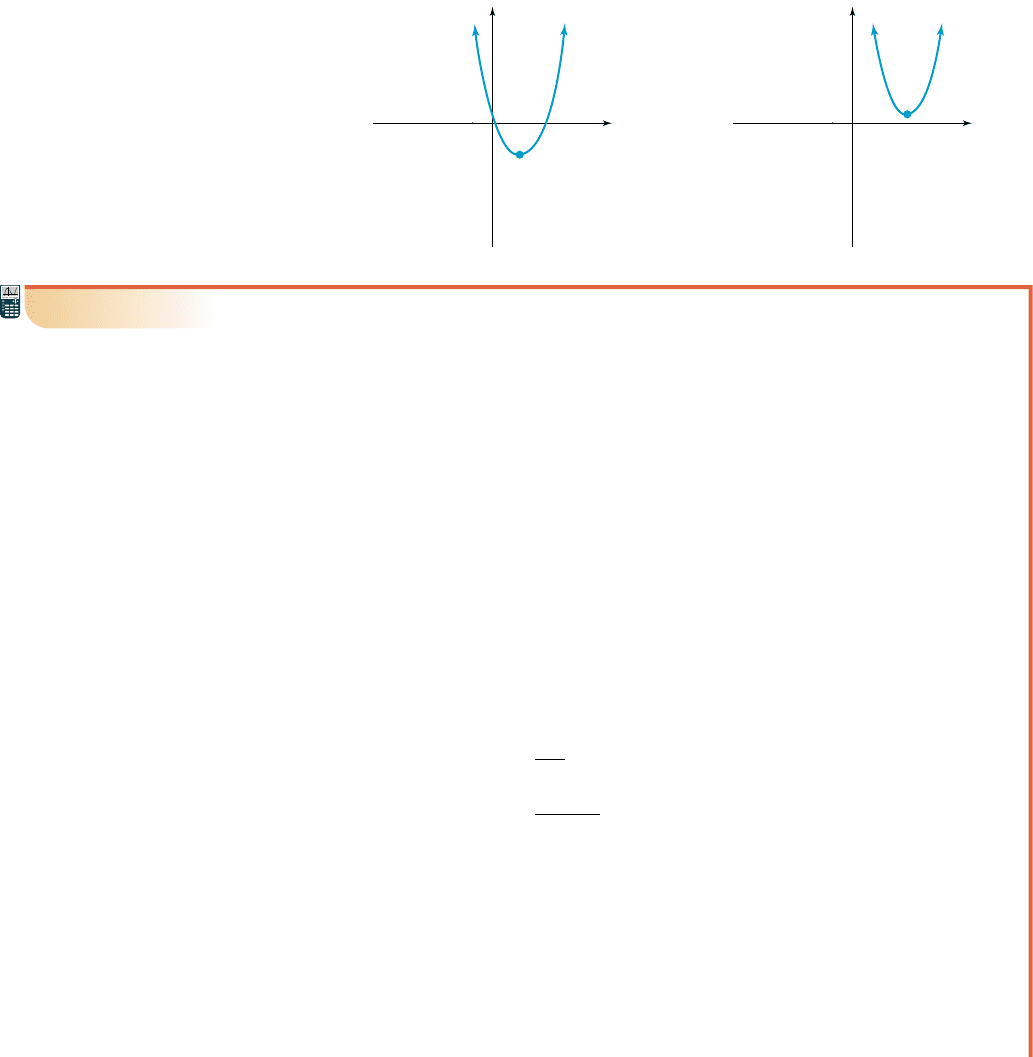
Recall that if the leading coefficient is positive and the vertex is below the x-axis
( ), the graph will have two x-intercepts (see Figure 3.44). If and the vertex
is above the x-axis ( ), the graph will not cross the x-axis (Figure 3.45). Similar
statements can be made for the case where a is negative.
k 7 0
a 7 0k 6 0
x
y
(h, k)
a 0
k 0
two x-intercepts
x
y
(h, k)
a 0
k 0
no x-intercepts
Figure 3.44
Figure 3.45
EXAMPLE 6
䊳
Modeling the Height of a Projectile—Football
In the 1976 Pro Bowl, NFL punter Ray Guy of the Oakland Raiders kicked the ball
so high it hit the scoreboard hanging from the roof of the New Orleans Superdome
(forcing officials to raise the scoreboard from about 90 ft to 200 ft). If we assume
the ball made contact with the scoreboard near the vertex of the kick, the function
is one possible model for the height of the ball, where h(t)
represents the height (in feet) after t sec.
a. What does the y-intercept of this function represent?
b. After how many seconds did the football reach its maximum height?
c. What was the maximum height of this kick?
d. To the nearest hundredth of a second, how long until the ball returned to the
ground (what was the hang time)?
Algebraic Solution
䊳
a. , meaning the ball was 1 ft off the ground when Ray Guy kicked it.
b. Since , we know the graph opens downward and has a maximum value.
To find the time needed to reach the maximum height, we use the vertex
formula with and :
vertex formula
substitute for
a
and 76 for
b
result
The ball reached its maximum height after 2.375 sec.
c. To find the maximum height, we substitute 2.375 for t [evaluate h(2.375)]:
given function
substitute 2.375 for
t
result
The ball reached a maximum height of 91.25 ft.
91.25
h12.37521612.3752
2
7612.3752 1
h1t216t
2
76t 1
2.375
16
76
21162
t
b
2a
b 76a 16
a 6 0
h102 1
h1t216t
2
76t 1
cob19545_ch03_314-328.qxd 8/10/10 8:15 PM Page 318
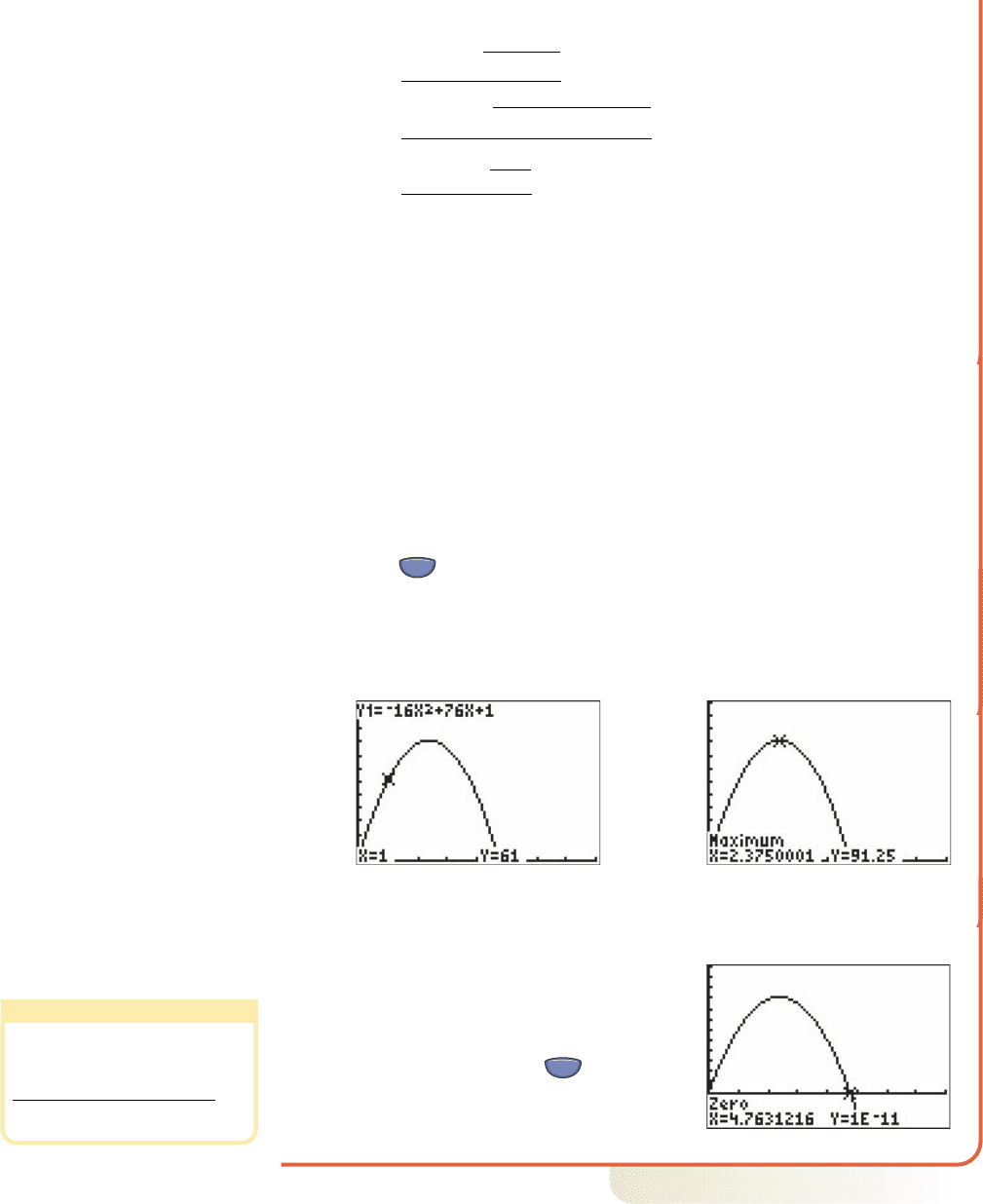
3–39 Section 3.3 Quadratic Functions and Applications 319
College Algebra G&M—
d. When the ball returns to the ground it has a height of 0 ft. Substituting 0 for
h(t) gives , which we solve using the quadratic formula.
quadratic formula
substitute for
a
, 76 for
b
, and 1 for
c
simplify
or
The punt had a hang time of just under 5 sec.
Graphical Solution
䊳
a. By inspection or using the TABLE, showing the ball was 1 ft from
the ground when it was kicked.
b. and c. Here we enter as Y
1
, then determine an appropriate
viewing window. We are once again limited to QI, since the time t and height h
must both be positive. Based on common experience (participation or
observation) in throwing or kicking balls in various activities, ,
seems to be a good place to begin for time t. For the value of Ymax
(having set ), we decide to just “aim high” being aware of human
limitations, and adjust the window afterward (it would be impossible for a
human to kick a football 250 ft high!). Using some combination of the
preceding we set , yielding the graph in Figure 3.46. Using the
sequence (CALC) 4:maximum with appropriate bounds shows the
vertex occurs at (2.375, 91.25) (Figure 3.47), meaning a maximum height of
, occurred 2.375 sec after the ball was kicked .1x 2.375291.25 ft 1y 91.252
2nd
Ymax 120
Ymin 0
Xmax 8
Xmin 0
16x
2
76x 1
h102 1
t ⬇ 4.763 t ⬇ 0.013
76 15840
32
16
76 21762
2
41162112
21162
t
b 2b
2
4ac
2a
0 16t
2
76t 1
8
120
0
0 8
120
0
0
Figure 3.46
Figure 3.47
d. Before using the Zeroes Method to find
the “hang time,” we reset the minimum
y-value to , to obtain a
frame that enables us to read the
information at the bottom of the screen,
without interfering with the graph (see
Worthy of Note). Using the (CALC)
2:zero option for the rightmost x-intercept,
we find the hang time is about 4.76 sec
(Figure 3.48).
Now try Exercises 47 through 52
䊳
2nd
Ymin 30
8
120
30
0
Figure 3.48
WORTHY OF NOTE
To find a frame of the kind
mentioned in Example 6(d), we can
use the formula
as a rule of thumb.
冟
current Ymax
冟
冟
current Ymin
冟
4
Ymin ⬇
cob19545_ch03_314-328.qxd 11/25/10 3:33 PM Page 319
