Coburn J.W., Herdlick J.D. College Algebra: Graphs and Models
Подождите немного. Документ загружается.


280 CHAPTER 2 More on Functions 2–94
College Algebra G&M—
28. Use a graphing calculator and the intersection-
of-graphs method to solve the inequality.
29. Graph the following piecewise-defined function
using a graphing calculator. Then use the
command to evaluate the function at
30. The data given shows the growth of the total U.S.
National Debt (in billions) for the years 1993 to
1999 , and for the years 2001 to 2007
, for each set of data, enter the data into a
graphing calculator, then
a. Set an appropriate window for viewing the
scatterplots, and determine if the associations are
linear or nonlinear.
b. If linear, find the regression equation for each
data set and graph both (as Y
1
and Y
2
) in the same
window (round to two decimal places).
c. During which 7-year period did the national debt
increase faster? How much faster?
12001 S 12
11993 S 12
f
1x2⫽ e
⫺x ⫹ 2 ⫺5 ⱕ x 6 ⫺2
1x ⫺ 22
2
⫺ 3 x ⱖ 1
x ⫽ 1.2.
TRACE
01.21x ⫺ 0.5206 0.4x ⫹ 1.4
22. During a table tennis tournament, the championship
game between J.W. and Mike took a dramatic and
unexpected turn. At one point in the game, J.W.
was losing 5–15. Facing a crushing loss, he
summoned all his willpower and battled on to
a 21–19 victory! Assuming the game score
relationship is linear, find the slope of the line
between these two scores and discuss its meaning
in this context.
23. Solve by factoring:
a.
b.
24. A theorem from elementary
geometry states, “A line
tangent to a circle is
perpendicular to the radius at
the point of tangency.” Find
the equation of the tangent
line for the circle and radius
shown.
25. A triangle has its vertices at
and (0, 8). Find the perimeter of the triangle
and determine whether or not it is a right
triangle.
Exercises 26 through 30 require the use of a graphing
calculator.
26. Use the zeroes method to solve the equation
Round your
answer to two decimal places.
27. Use a graphing calculator to graph the circle defined
by 1x ⫹ 22
2
⫹ y
2
⫽ 4.
2.71x ⫺ 32⫹ 0.3 ⫽ 1.8 ⫺ 1.21x ⫹ 42.
1⫺4, 52, 14, ⫺12,
x
3
⫹ 5x
2
⫺ 15 ⫽ 3x
6x
2
⫺ 7x ⫽ 20
Year 1993 to 2001 to
(scaled) 1999 2007
1 4.5 5.9
2 4.8 6.4
3 5.0 7.0
4 5.3 7.6
5 5.5 8.2
6 5.6 8.7
7 5.8 9.2
(1, 2)
(⫺1, 1)
x
y
54321⫺5⫺4⫺3⫺2⫺1
⫺1
⫺2
⫺3
⫺4
⫺5
2
3
4
5
1
cob19545_ch02_271-280.qxd 11/1/10 8:37 AM Page 280

College Algebra Graphs & Models—
Quadratic Functions
and Operations on
Functions
CHAPTER OUTLINE
3.1 Complex Numbers 282
3.2 Solving Quadratic Equations and Inequalities 292
3.3 Quadratic Functions and Applications 313
3.4 Quadratic Models; More on Rates of Change 328
3.5 The Algebra of Functions 340
3.6 The Composition of Functions
and the Difference Quotient 352
CHAPTER CONNECTIONS
Whether it be in business, industry, animal
science, space, sports, or some other sector,
decision makers are preoccupied with maximum
and minimum values. Questions concerning
minimum cost, maximum efficiency, least
amount of waste, greatest amount of area, and
other similar questions require and deserve a
great deal of attention. In this chapter, we’ll
learn to calculate some of these maximums and
minimums, like the height achieved by a
motocross or snowboarding athlete in the
performance of jumps. This application appears
as Exercise 51 in Section 3.3.
Check out these other real-world connections:
䊳
Projectile Height (Section 3.2, Exercise 161)
䊳
Pricing Strategies (Section 3.3, Exercise 44)
䊳
Start-up Times (Section 3.4, Exercise 47)
䊳
Distribution Distance (Section 3.5, Exercise 75)
281
cob19545_ch03_281-292.qxd 8/10/10 6:03 PM Page 281

3.1 Complex Numbers
For centuries, even the most prominent mathematicians refused to work with equations
like Using the principal of square roots gave the “solutions” and
which they found baffling and mysterious, since there is no real number
whose square is . In this section, we’ll see how this dilemma was finally resolved.
A. Identifying and Simplifying Imaginary and Complex Numbers
The equation has no real solutions, since the square of any real number is
positive. But if we apply the principle of square roots we get and
which seem to check when substituted into the original equation:
original equation
(1) substitute for
x
✓ answer “checks”
(2) substitute for
x
✓ answer “checks”
This observation likely played a part in prompting Renaissance mathematicians to
study such numbers in greater depth, as they reasoned that while these were not real
number solutions, they must be solutions of a new and different kind. Their study even-
tually resulted in the introduction of the set of imaginary numbers and the imaginary
unit i, as follows.
Imaginary Numbers and the Imaginary Unit
1 1 0
11 1112
2
1 0
1 1 0
11 1112
2
1 0
x
2
1 0
x 11
,
x 11
x
2
1
1
x 11
,
x 11
x
2
1 0.
282 3–2
College Algebra Graphs & Models—
LEARNING OBJECTIVES
In Section 3.1 you will see how we can
A. Identify and simplify
imaginary and complex
numbers
B. Add and subtract complex
numbers
C. Multiply complex
numbers and find
powers of i
D. Divide complex numbers
• Imaginary numbers are those of
the form where k is
a positive real number.
1k
,
• The imaginary unit i represents
the number whose square is
i 11
, where i
2
1
1:
As a convenience to understanding and working with imaginary numbers, we
rewrite them in terms of i, allowing that the product property of radicals
still applies if only one of the radicands is negative. For we
have More generally, we simply make the following
statement regarding imaginary numbers.
Rewriting Imaginary Numbers
For any positive real number k,
For and we have:
and we say the expressions have been simplified and written in terms of i. Note that for
we’ve written the result with the unit “i” in front of the radical to prevent it
being interpreted as being under the radical. In symbols,
The solutions to also serve to illustrate that for there are two
solutions to namely, and In other words, every negative number
has two square roots, one positive and one negative. The first of these, is called
the principal square root of k.
i1k
,
i1k
.i1kx
2
k,
k 7 0,x
2
1
2i15
215i 215i.
120
2i15, 4i
i14
#
5 i142
120
i120 116 i116
120116
1k i1k.
11
#
3 1113 i13.
13
,11AB 1A1B2
WORTHY OF NOTE
It was René Descartes (in 1637)
who first used the term imaginary
to describe these numbers;
Leonhard Euler (in 1777) who
introduced the letter i to represent
and Carl F. Gauss (in 1831)
who first used the phrase complex
number to describe solutions that
had both a real number part and
an imaginary part. For more on
complex numbers and their story,
see www.mhhe.com/coburn
11;
cob19545_ch03_281-292.qxd 8/10/10 6:03 PM Page 282
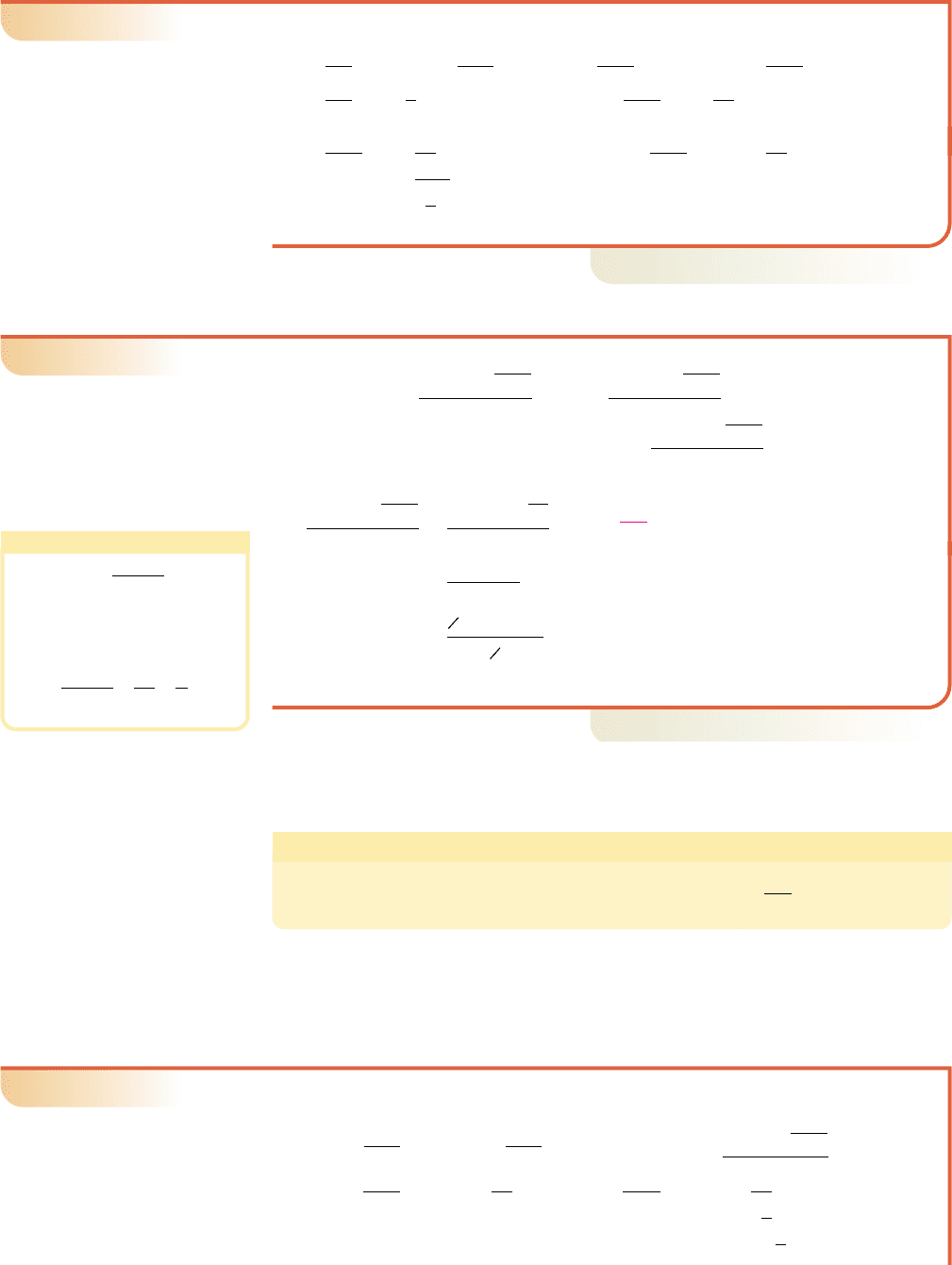
EXAMPLE 1
䊳
Simplifying Imaginary Numbers
Rewrite the imaginary numbers in terms of i and simplify if possible.
a. b. c. d.
Solution
䊳
a. b.
c. d.
Now try Exercises 7 through 12
䊳
EXAMPLE 2
䊳
Writing an Expression in Terms of i
The numbers and are not real, but are known
to be solutions of Simplify
Solution
䊳
Using the i notation, we have
write in
i
notation
simplify
factor numerator and reduce
result
Now try Exercises 13 through 16
䊳
The result in Example 2 contains both a real number part and an imagi-
nary part Numbers of this type are called complex numbers.
Complex Numbers
Complex numbers are those that can be written in the form ,
where a and b are real numbers and
The expression is called the standard form of a complex number. From
this definition we note that all real numbers are also complex numbers, since is
complex with In addition, all imaginary numbers are complex numbers, since
is a complex number with (See Figure 3.1).
EXAMPLE 3
䊳
Writing Complex Numbers in Standard Form
Write each complex number in the form and identify the values of a and b.
a. b. c. 7 d.
Solution
䊳
a. b.
a 0, b 213
a 2, b 7
0 2i13
2 7i
112
0 i112 2 149 2 i149
4 3125
20
1122 149
a bi,
a 00 bi
b 0.
a 0i
a bi
i 11
.
a bi
12i2.
132
3 2i
2
13 2i2
2
6 4i
2
116
6 116
2
6 i116
2
6 116
2
.x
2
6x 13 0.
x
6 116
2
x
6 116
2
12i 2i16
3i142 i14
#
6
3116 3i116 124 i124
9i
181
i18117 i17
311612418117
3–3 Section 3.1 Complex Numbers 283
College Algebra Graphs & Models—
WORTHY OF NOTE
The expression from the
solution of Example 2 can also be
simplified by rewriting it as two
separate terms, then simplifying
each term:
3 2i.
6 4i
2
6
2
4i
2
6 4i
2
cob19545_ch03_281-292.qxd 8/10/10 6:03 PM Page 283
c. d.
Now try Exercises 17 through 24
䊳
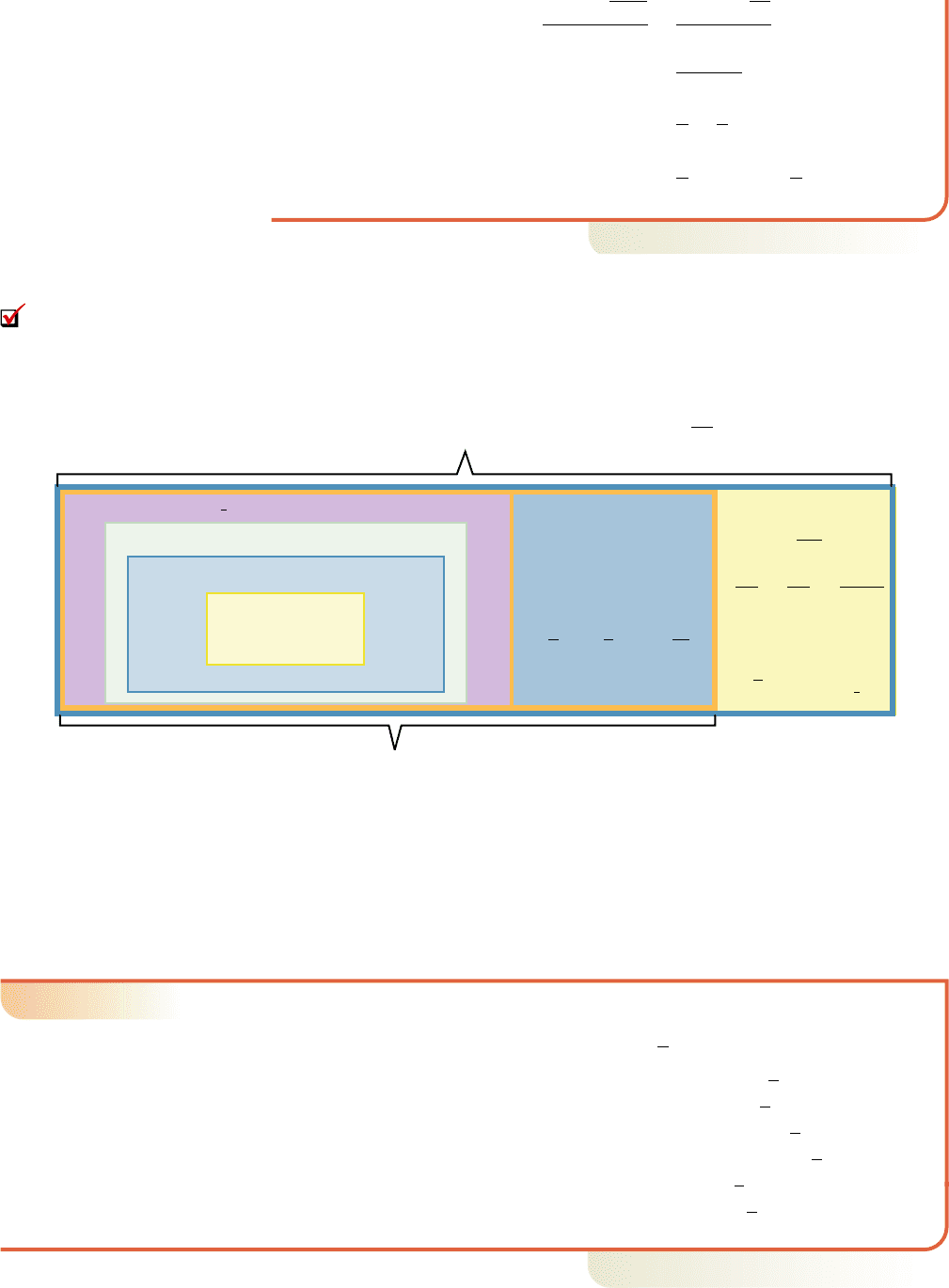
Complex numbers complete the development of our “numerical landscape.” Sets
of numbers and their relationships are represented in Figure 3.1, which shows how
some sets of numbers are nested within larger sets and highlights the fact that complex
numbers consist of a real number part (any number within the orange rectangle), and
an imaginary number part (any number within the yellow rectangle).
a
1
5
or 0.2, b
3
4
or 0.75
1
5
3
4
i
4 15i
20
a 7, b 0
4 3125
20
4 3i125
20
7 7 0i
284 CHAPTER 3 Quadratic Functions and Operations on Functions 3–4
College Algebra Graphs & Models—
A. You’ve just seen how
we can identify and simplify
imaginary and complex
numbers
R (real): All rational and irrational numbers
Q (rational):
{
p
, where p, q z and q 0
}
q
3
4
Z (integer): {... , 2, 1, 0, 1, 2, ...}
W (whole): {0, 1, 2, 3, ...}
N (natural):
{1, 2, 3, ...}
C (complex): Numbers of the form a bi, where a, b R and i 兹1.
I (imaginary):
Numbers of the form
兹k,
where k > 0
兹7 兹9 兹0.25
a bi,
where a 0
i兹3 5i i
兹2, 兹7, 兹10,
H (irrational):
Numbers that
cannot be written
as the ratio
of two integers;
a real number
that is not rational.
0.070070007...
and so on.
B. Adding and Subtracting Complex Numbers
The sum and difference of two polynomials is computed by identifying and combining
like terms. The sum or difference of two complex numbers is computed in a similar
way, by adding the real number parts from each, and the imaginary parts from each.
Notice in Example 4 that the commutative, associative, and distributive properties also
apply to complex numbers.
EXAMPLE 4
䊳
Adding and Subtracting Complex Numbers
Perform the indicated operation and write the result in form.
a. b.
Solution
䊳
a. original sum b.
distribute distribute
commute terms commute terms
group like terms group like terms
result result
,
Now try Exercises 25 through 30
䊳
b 4 12a 3a 3, b 5
3 14 12
2i3 5i
15 22 314i2 i12
4 32 1524 13i 2i2
5 2 14i2 i12
2 152 3i 2i
5 4i 2 i12
2 3i 152 2i
15 4i2 12 i12
212 3i2 15 2i2
15 4i2 12 i12
212 3i2 15 2i2
a bi
original
difference
Figure 3.1
cob19545_ch03_281-292.qxd 8/10/10 6:03 PM Page 284

Most graphing calculators are programmed to work
with imaginary and complex numbers, though for
some models the calculator must be placed in com-
plex number mode. After pressing the key
(located to the right of the option key), the
screen shown in Figure 3.2 appears and we use
the arrow keys to access “ ” and active this
mode (by pressing ). Once active, we can validate
our previous statements about imaginary numbers
(Figure 3.3), as well as verify our previous calculations like those in Examples 3(a), 3(d),
and 4(a) (Figure 3.4). Note the imaginary unit i is the option for the decimal point.
2nd
ENTER
a bi
2nd
MODE
3–5 Section 3.1 Complex Numbers 285
College Algebra Graphs & Models—
Figure 3.3 Figure 3.4
B. You’ve just seen how
we can add and subtract
complex numbers
C. Multiplying Complex Numbers; Powers of i
The product of two binomials is computed using the distributive property and the
F-O-I-L process, then combining like terms. The product of two complex numbers is
computed in a similar manner. If any result gives a factor of remember that
EXAMPLE 5
䊳
Multiplying Complex Numbers
Find the indicated product and write the answer in form.
a. b.
c. d.
Solution
䊳
a. rewrite in terms of
i
b.
simplify distribute
multiply
result simplify
c. d.
F-O-I-L
result result
Now try Exercises 31 through 44
䊳
CAUTION
䊳
When computing with imaginary and complex numbers, always write the square root of
a negative number in terms of i before you begin, as shown in Examples 5(a) and 5(b).
Otherwise we get conflicting results, since if we multiply the
radicands first, which is an incorrect result because the original factors were imaginary.
See Exercise 80.
14
19 136 6
13 0i 29 14i
i
2
1 4 9112i
2
1 24 6i 120i2 152112
13i 2
2
9i
2
4 9i
2
i
#
i i
2
24 6i 120i2 152i
2
1A B21A B2 A
2
B
2
122
2
13i2
2
162142 6i 15i2142 15i21i2
12 3i212 3i216 5i214 i2
312
2i16
2i16 3121i
2
12 6 0i
i
2
1 2i16 1121912 6i
2
2i16 i
2
118 2i
#
3i
16
12 132 i1612 i1321419 i14
#
i19
12 3i212 3i216 5i214 i2
16
12 1321419
a bi
i
2
1.i
2
,
rewrite in
terms of
i
standard form
Figure 3.2
cob19545_ch03_281-292.qxd 8/10/10 6:03 PM Page 285

As before, computations with complex numbers are easily checked using a graphing
calculator. The results from Example 5(a), 5(c), and 5(d) are verified in Figure 3.5. For
Example 5(b), the coefficients are irrational numbers that run off of the screen (Figure 3.6).
To check this answer, we could compare the decimal forms of and to the
given decimal numbers, but instead we chose to simply check the product using division
(to check the result of a multiplication, divide by one of the factors). Dividing the
result by the factor , gives 2 1.732050808i, which we easily recognize as the
other original factor
✓.2 i13
16
216312
286 CHAPTER 3 Quadratic Functions and Operations on Functions 3–6
College Algebra Graphs & Models—
Figure 3.6Figure 3.5
Recall that expressions and are called binomial conjugates. In the
same way, and are called complex conjugates. Note from Example 5(d)
that the product of the complex number with its complex conjugate is a
real number. This relationship is useful when rationalizing expressions with a complex
number in the denominator, and we generalize the result as follows:
Product of Complex Conjugates
For a complex number and its conjugate
their product is the real number
Showing that is left as an exercise (see Exercise 79),
but from here on, when asked to compute the product of complex conjugates, simply
refer to the formula as illustrated here: or 34. See
Exercises 45 through 48.
These operations on complex numbers enable us to verify complex solutions by
substitution, in the same way we verify solutions for real numbers. In Example 2 we
stated that was one solution to This is verified here.
EXAMPLE 6
䊳
Checking a Complex Root by Substitution
Verify that is a solution to
Solution
䊳
original equation
substitute for
x
square and distribute
simplify
combine terms
✓
A calculator verification is also shown.
Now try Exercises 49 through 56
䊳
0 0
112i 12i 0; i
2
12 9 142 5 0
9 12i 4i
2
12i 5 0
132
2
213212i2 12i2
2
18 12i 13 0
3 2i 13 2i2
2
613 2i2 13 0
x
2
6x 13 0
x
2
6x 13 0.x 3 2i
x
2
6x 13 0.x 3 2i
13 5i213 5i2 132
2
5
2
1a bi21a bi2 a
2
b
2
1a bi21a bi2 a
2
b
2
a
2
b
2
;1a bi21a bi2
a bi,a bi
a bia bi
a bia bi
2x 52x 5
WORTHY OF NOTE
Notice that the product of a
complex number and its conjugate
also gives us a method for factoring
the sum of two squares using
complex numbers! For the
expression the factored
form would be For
more on this idea, see Exercise 79.
1x 2i21x 2i2.
x
2
4,
cob19545_ch03_281-292.qxd 8/10/10 6:03 PM Page 286

3–7 Section 3.1 Complex Numbers 287
College Algebra Graphs & Models—
EXAMPLE 7
䊳
Checking a Complex Root by Substitution
Show that is a solution of
Solution
䊳
original equation
substitute for
x
square and distribute
✓ solution checks
A calculator verification is also shown.
Now try Exercises 57 through 60
䊳
The imaginary unit i has another interesting and useful property. Since
and it follows that and We can now
simplify any higher power of i by rewriting the expression in terms of , since
for any natural number n.
Notice the powers of i “cycle through” the four values and 1. In more ad-
vanced classes, powers of complex numbers play an important role, and next we learn
to reduce higher powers using the power property of exponents and Essen-
tially, we divide the exponent on i by 4, then use the remainder to compute the value of
the expression. For remainder 3, showing
EXAMPLE 8
䊳
Simplifying Higher Powers of i
Simplify:
a. b. c. d.
Solution
䊳
a. b.
c. d.
Now try Exercises 61 and 62
䊳
While powers of i can likewise be checked on a graph-
ing calculator, the result must be interpreted carefully.
For instance, while we know , the calculator
returns an answer of 1 2
E
13i (Figure 3.7). To
interpret this result correctly, we identify the real
number part as , and the imaginary part as
, which due to limitations in the technology
is approximated by 2
E
(an
extremely small number).
13 2 10
13
b 0
a 1
i
22
1
i i
112
18
1i2 112
14
i
i
75
1i
4
2
18
#
1i
3
2 i
57
1i
4
2
14
#
i
75 4 18 remainder 3 57 4 14 remainder 1
1 1
112
7
112
5
112
i
28
1i
4
2
7
i
22
1i
4
2
5
#
1i
2
2
28 4 7 remainder 0 22 4 5 remainder 2
i
75
i
57
i
28
i
22
i
35
1i
4
2
8
#
i
3
i.i
35
, 35 4 8
i
4
1.
i, 1, i
i
8
1i
4
2
2
1 i
4
1
i
7
i
4
#
i
3
i i
3
i
i
6
i
4
#
i
2
1 i
2
1
i
5
i
4
#
i i i i
1i
4
2
n
1
i
4
i
4
1i
2
2
2
1.i
3
i
2
#
i 112i ii
2
1,
i 11
7 7
1i132
2
3 4 4i13 3 8 4i13 7
4 4i13
1i132
2
8 4i13 7
2 i13 12 i132
2
412 i1327
x
2
4x 7
x
2
4x 7.x 2 i13
C. You’ve just seen how
we can multiply complex
numbers and find powers of i
Figure 3.7
cob19545_ch03_281-292.qxd 11/25/10 3:25 PM Page 287

D. Division of Complex Numbers
Since expressions like actually have a radical in the denominator.
To divide complex numbers, we simply apply our earlier method of rationalizing
denominators (Section R.6), but this time using a complex conjugate.
EXAMPLE 9
䊳
Dividing Complex Numbers
Divide and write each result in form.
a. b. c.
Solution
䊳
a. b.
c.
convert to
i
notation
simplify
The expression can be further simplified by reducing common factors.
factor and reduce
Now try Exercises 63 through 68
䊳
As mentioned, operations on complex numbers can be checked using inverse
operations, just as we do for real numbers. To check the division from Example 9b,
we multiply by the divisor :
✓
Several checks are asked for in the exercises. A calcu-
lator check is shown for Example 9(a) in Figure 3.8,
where we note that converting the coefficients to
rational numbers (where possible): Frac,
makes the result easier to understand. As you read and
interpret this result, note the intent is , which
must not be confused with . The latter is an
entirely different (and incorrect) number.
5
13
1
13i
5
13
1
13
i
1:䉴
MATH
3 i
2 i 1
2 i 112
11 i212 i2 2 i 2i i
2
2 i1 i
611 i2
311 i2
2 0i
6 6i
3 3i
6 136
3 19
6 i136
3 i19
1 i
5
13
1
13
i
5 5i
5
5
5
5i
5
10
26
2
26
i
6 5i 112
5
10 2i
26
6 3i 2i i
2
2
2
1
2
215 i2
5
2
1
2
3 i
2 i
3 i
2 i
#
2 i
2 i
2
5 i
2
5 i
#
5 i
5 i
6 136
3 19
3 i
2 i
2
5 i
a bi
3 i
2 i
i 11,
288 CHAPTER 3 Quadratic Functions and Operations on Functions 3–8
College Algebra Graphs & Models—
D. You’ve just seen how
we can divide complex
numbers
Figure 3.8
cob19545_ch03_281-292.qxd 8/10/10 6:03 PM Page 288

3–9 Section 3.1 Complex Numbers 289
College Algebra Graphs & Models—
3.1 EXERCISES
2. The product gives the real
number .
13 2i213 2i2
䊳
CONCEPTS AND VOCABULARY
Fill in each blank with the appropriate word or phrase. Carefully reread the section, if necessary.
1. Given the complex number its complex
conjugate is .
3 2i,
䊳
DEVELOPING YOUR SKILLS
Simplify each radical (if possible). If imaginary, rewrite
in terms of i and simplify.
7. a. b.
c. d.
8. a. b.
c. d.
9. a. b.
c. d.
10. a. b.
c. d.
11. a. b.
c. d.
12. a. b.
c. d.
Simplify each expression, writing the result in terms of i.
13. a. b.
14. a. b.
15. a. b.
16. a. b.
12 1200
8
6 172
4
10 150
5
8 116
2
4 3120
2
16 18
2
6 127
3
2 14
2
A
49
75A
45
36
153117
A
9
32A
12
25
131119
218131144
175132
2193125
150118
198164
11691100
172127
1491144
Write each complex number in the standard form
and clearly identify the values of a and b.
17. a. 5 b. 3i
18. a. b.
19. a. b.
20. a. b.
21. a. b.
22. a. b.
23. a. b.
24. a. b.
Perform the addition or subtraction. Write the result in
form. Check your answers using a calculator.
25. a.
b.
c.
26. a.
b.
c.
27. a.
b.
c. 16 5i2 14 3i2
15 2i2 13 2i2
12 3i2 15 i2
1120
132 115 1122
113
122 1112 182
17 172
2 18 1502
111 1108
2 12 1482
13 125
2 11 1812
112 14
2 17 192
a ⴙ bi
8 127
6
21 163
12
5 1250
10
14 198
8
7 175
2 148
5 1274 150
175
15
3136
132
8
2181
4i2
a ⴙ bi
3. If the expression is written in the standard
form then and .
b a a bi,
4 6i12
2
4. For , , , , and
, , , , and .
i
9
i
7
i
5
i
3
i
8
i
6
i
4
i
2
i 11
5. Discuss/Explain which is correct:
a.
b. 14
#
19 2i
#
3i 6i
2
6
14
#
19 1142192 136 6
6. Compare/Contrast the product
with the product What is the
same? What is different?
11 i12
211 i132.
11 12
211 132
cob19545_ch03_281-292.qxd 11/25/10 3:26 PM Page 289
