Coburn J.W., Herdlick J.D. College Algebra: Graphs and Models

Подождите немного. Документ загружается.

On the left, our ﬁnal solutions are or . The general solution is

called the quadratic formula, which can be used to solve any equation belonging to

the quadratic family.

Quadratic Formula

If with a, b, and and then

also written

CAUTION

䊳

It’s very important to note the values of a, b, and c come from an equation written in stan-

dard form. For and but In standard form we have

and note the value for use in the formula is actually

EXAMPLE 5

䊳

Solving Quadratic Equations Using the Quadratic Formula

Solve using the quadratic formula. State the solution(s) in both exact

and approximate form. Check one of the exact solutions in the original equation.

Solution

䊳

Begin by writing the equation in standard form and identifying the values of a, b,

and c.

original equation

standard form

substitute 4 for

, ⴚ8 for

, and 1 for

simplify

simplify radical (see following CAUTION)

or exact solutions

or approximate solutions

Check

䊳

original equation

substitute for

square binomial; distribute

distribute

✓ result checks

A graphing calculator check is also shown.

Now try Exercises 61 through 90

䊳

8 ⫹ 413 ⫽ 8 ⫹ 413

4 ⫹ 413 ⫹ 3 ⫹ 1 ⫽ 8 ⫹ 413

4 c1 ⫹ 2 a

b⫹

d⫹ 1 ⫽ 8 ⫹ 413

1 ⫹

4 a1 ⫹

⫹ 1 ⫽ 8 a1 ⫹

4 x

⫹ 1 ⫽ 8x

x ⬇ 0.13 x ⬇ 1.87

x ⫽ 1 ⫺

x ⫽ 1 ⫹

x ⫽

8 ⫾ 413

⫽

⫾

413

x ⫽

8 ⫾ 164 ⫺ 16

⫽

8 ⫾ 148

x ⫽

⫺1⫺82⫾ 21⫺82

⫺ 4142112

2142

a ⫽ 4, b ⫽⫺8, c ⫽ 1

4 x

⫺ 8x ⫹ 1 ⫽ 0

4 x

⫹ 1 ⫽ 8x

c ⫽ 7.3x

⫺ 5x ⫹ 7 ⫽ 0,

c ⫽⫺7!b ⫽⫺5,3x

⫺ 5x ⫽⫺7, a ⫽ 3

x ⫽

⫺b ⴞ 2b

⫺ 4ac

x ⫽

⫺b ⴚ 2b

⫺ 4ac

;x ⫽

⫺b ⴙ 2b

⫺ 4ac

a ⫽ 0,c 僆⺢ax

⫹ bx ⫹ c ⫽ 0,

x ⫽⫺

x ⫽⫺1

300 CHAPTER 3 Quadratic Functions and Operations on Functions 3–20

College Algebra G&M—

cob19545_ch03_293-313.qxd 8/10/10 6:07 PM Page 300

CAUTION

䊳

For be careful not to incorrectly “cancel the eights” as in

No! Use a calculator to verify that the results are not equivalent. Both terms in the numer-

ator are divided by 8 and we must either rewrite the expression as separate terms (as

above) or factor the numerator to see if the expression simpliﬁes further:

which is equivalent to

The Discriminant of the Quadratic Formula

The conclusions we reached graphically in Figure 3.14 regarding the nature of number

of quadratic roots can now be seen algebraically through a closer look at the quadratic

formula. For any real-valued expression X, recall that represents a real number

only for Since the quadratic formula contains the radical the

expression called the discriminant, will determine the nature (real or com-

plex) and the number of solutions to a given quadratic equation.

The Discriminant of the Quadratic Formula

For , where a, b, c and ,

1. If , 2. If , 3. If ,

there are two there is one real there are two

real roots (repeated) root nonreal roots

These ideas are further illustrated here, by comparing the value of the discriminant

with the graph of the related function shown below each calculation.

⫺ 4ac 6 0b

⫺ 4ac ⫽ 0b

⫺ 4ac 7 0

a ⫽ 0⺢僆f

1x2⫽ ax

⫹ bx ⫹ c

⫺ 4ac,

⫺ 4ac,X ⱖ 0.

1 ⫾

8 ⫾ 413

⫽

12 ⫾ 132

⫽

2 ⫾ 13

⫾ 413

⫽ 1 ⫾ 413.

8 ⫾ 413

3–21 Section 3.2 Solving Quadratic Equations and Inequalities 301

College Algebra G&M—

, f has two real roots16 7 0

⫽ 16

⫽ 16 ⫺ 0

⫺ 4ac ⫽ 1⫺42

⫺ 4112102

a ⫽ 1, b ⫽⫺4, c ⫽ 0

1x2⫽ x

⫺ 4x 2.

, g has one real root0 ⫽ 0

⫽ 0

⫽ 16 ⫺ 16

⫺ 4ac ⫽ 1⫺42

⫺ 4112142

a ⫽ 1, b ⫽⫺4, c ⫽ 4

g1x2⫽ x

⫺ 4x ⫹ 4 3.

, h has two nonreal roots⫺4 6 0

⫽⫺4

⫽ 16 ⫺ 20

⫺ 4ac ⫽ 1⫺42

⫺ 4112152

a ⫽ 1, b ⫽⫺4, c ⫽ 5

h1x2⫽ x

⫺ 4x ⫹ 5

⫺5

Finally, we note from (3) and the structure of the quadratic formula, that the

complex solutions must occur in conjugate pairs.

Complex Solutions

The complex solutions of a quadratic equation with real coefﬁcients

must occur in conjugate pairs.

If is a solution, then is also a solution.a ⫺ bia ⫹ bi

cob19545_ch03_293-313.qxd 8/10/10 6:07 PM Page 301

Further analysis of the discriminant reveals even more concerning the nature of

quadratic solutions. Namely, if a, b, and c are rational and the discriminant is

1. zero, the original equation is a perfect square trinomial.

2. a perfect square, there will be two rational roots which means

the original equation can be solved by factoring.

3. not a perfect square, there will be two irrational roots.

See Exercises 91 through 102.

EXAMPLE 6

䊳

Solving Quadratic Equations Using the Quadratic Formula

Solve:

Solution

䊳

With , and the discriminant becomes ,

showing there will be two complex roots. The quadratic formula then yields

quadratic formula

substitute 2 for

and ⴚ6 for

simplify, write in

form

solutions are complex conjugates

A calculator check is shown in Figures 3.25 and 3.26.

Now try Exercises 103 through 108

䊳

Summary of Solution Methods for ax

ⴙ bx ⴙ c ⴝ 0

1. If : isolate x

and use the square root property of equality.

2. If : factor out the GCF and use the zero product property.

3. If no coefﬁcient is zero, you can attempt to solve by

a. factoring b. completing the square c. using the quadratic formula

d. using the intersection-of-graphs method e. using the zeroes method

⫹ bx ⫽ 0c ⫽ 0,

⫹ c ⫽ 0b ⫽ 0,

Figure 3.25, 3.26

x ⫽

⫾

x ⫽

6 ⫾ 2i

⫺ 4ac ⫽⫺4, x ⫽

⫺1⫺62⫾ 1⫺4

2122

x ⫽

⫺b ⫾ 2b

⫺ 4ac

1⫺62

⫺ 4122152⫽⫺4c ⫽ 5,a ⫽ 2, b ⫽⫺6

⫺ 6x ⫹ 5 ⫽ 0.

302 CHAPTER 3 Quadratic Functions and Operations on Functions 3–22

College Algebra G&M—

D. You’ve just seen how

we can solve quadratic

equations using the quadratic

formula and the discriminant

WORTHY OF NOTE

While it’s possible to solve by

completing the square if is a

fraction or an odd number (see

Example 4), the process is usually

most efﬁcient when is an even

number. This is one observation

you could use when selecting a

solution method.

cob19545_ch03_293-313.qxd 8/10/10 6:07 PM Page 302

EXAMPLE 7

䊳

Solving a Quadratic Inequality

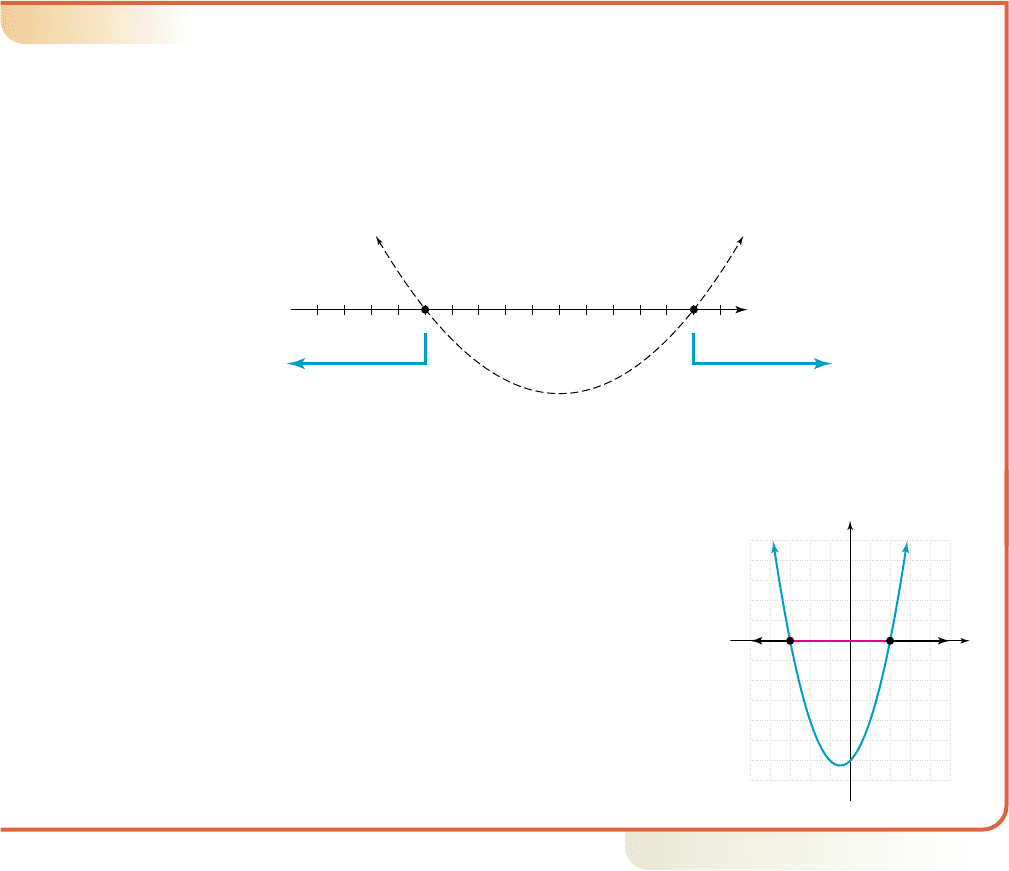
For , solve .

Analytical Solution

䊳

The graph of f will open upward since . Factoring gives ,

with zeroes at and 2. Using the x-axis alone (since graphing the function is not

our focus), we plot ( , 0) and (2, 0) and visualize a parabola opening upward

through these points (Figure 3.27).

The diagram clearly shows the graph is above the x-axis (outputs are positive)

when or when . The solution is .

Graphical Solution

䊳

The complete graph of f shown in Figure 3.28

conﬁrms the analytical solution. For the intervals

of the domain shown in bold ,

the graph is above the x-axis . For the

portion shown in red, the graph is below the

x-axis .

Now try Exercises 109 through 120

䊳

When solving general inequalities, zeroes of multiplicity continue to play a role.

In Example 7, the zeroes of f were both of multiplicity 1, and the graph crossed the

x-axis at these points. In other cases, the zeroes may have even multiplicity.

1x26 02

1x27 02

1⫺q, ⫺32 ´ 12, q2

x 僆 1⫺q, ⫺32 ´ 12, q2x 7 2x 6 ⫺3

When x  3,

the graph is above

the x-axis,

f(x)  0.

When x  2,

the graph is above

the x-axis,

f(x)  0.

When 3  x  2,

the graph is below

the x-axis,

f(x)  0.

a  0

0 1 2

5 4 3 2 1

⫺3

1x2⫽ 1x ⫹ 321x ⫺ 22a 7 0

1x27 0f 1x2⫽ x

⫹ x ⫺ 6

3–23 Section 3.2 Solving Quadratic Equations and Inequalities 303

College Algebra G&M—

Figure 3.27

55

5

f(x)  x

 x  6

Figure 3.28

E. Quadratic Inequalities

The study of quadratic inequalities is simply an extension of our earlier work in ana-

lyzing functions (Section 2.1). While we’ve developed the ability to graph a variety of

new functions, the solution set for an inequality will still be determined by analyzing

the behavior of the function at its zeroes. The key idea is to recognize the following

statements are synonymous:

1. . 2. Outputs are positive. 3. The graph is above the x-axis.

Similar statements can be made using the other inequality symbols.

Solving a quadratic inequality only requires that we (a) locate any real zeroes of

the function and (b) determine whether the graph opens upward or downward. If there

are no x-intercepts, the graph is entirely above the x-axis (output values are positive),

or entirely below the x-axis (output values are negative), making the solution either all

real numbers or the empty set.

1x27 0

cob19545_ch03_293-313.qxd 11/25/10 3:28 PM Page 303

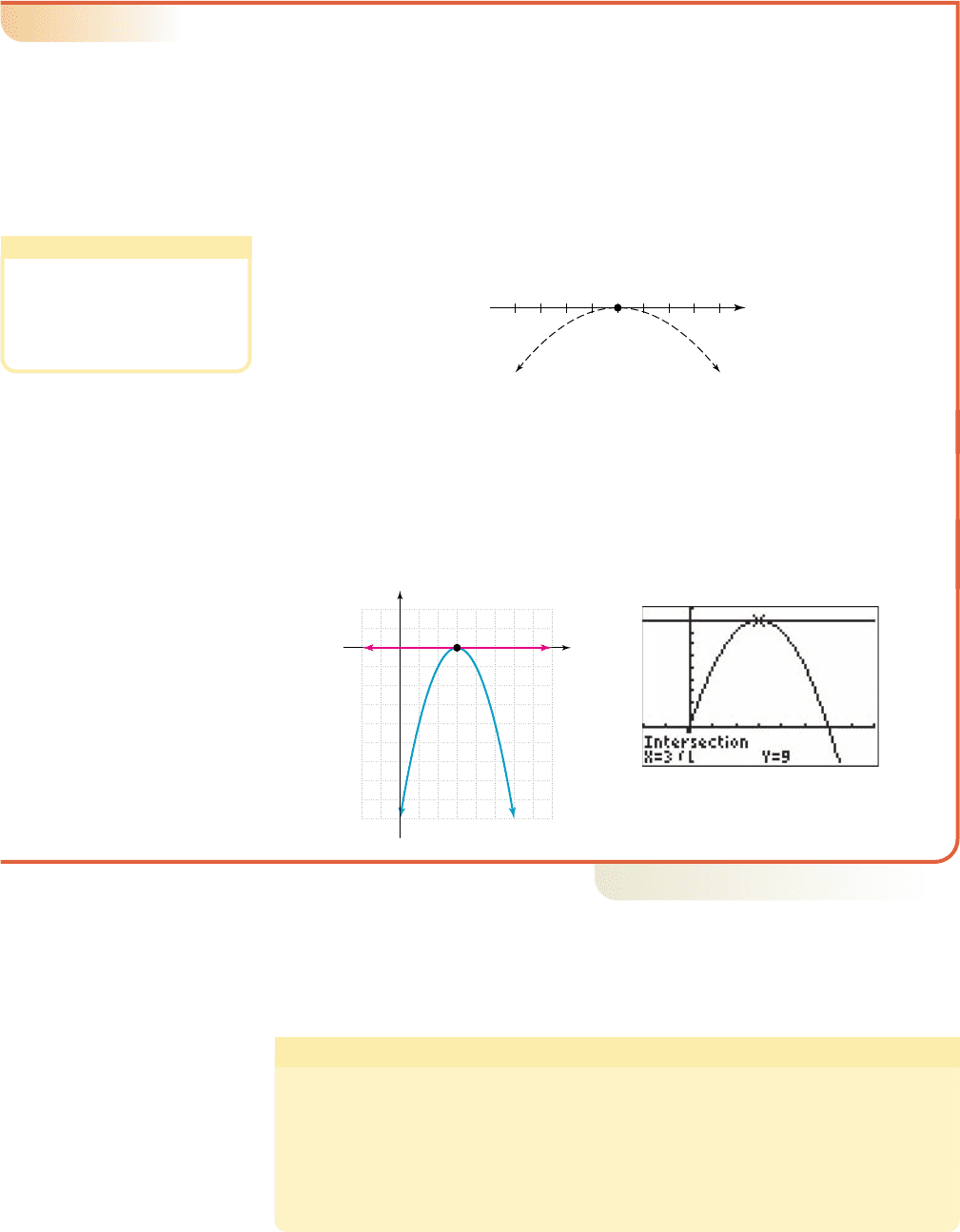
Graphical Solution

䊳

The complete graph of g shown in Figure 3.30 conﬁrms the analytical solution

(using the zeroes method). For the intervals of the domain shown in red:

, the graph of g is below the x-axis . The point (3, 0)

is on the x-axis . As with the analytical solution, the solution to this

“less than or equal to” inequality is all real numbers. A calculator check of the

original inequality is shown in Figure 3.31.

Now try Exercises 121 through 132

䊳

As an alternative to the Zeroes Method, the Interval Test Method can be used to

solve quadratic inequalities. Using the fact that all polynomials are continuous, test

values are selected from certain intervals of the domain and substituted into the origi-

nal function.

Interval Test Method for Solving Inequalities

1. Find all real roots of the related equation (if they exist) and

plot them on the x-axis.

2. Select any convenient test value from each interval created

by the zeroes, and substitute these into the function.

3. The sign of the function at these test values will be the sign

of the function for all values of x in this interval.

62

8

g(x)

⫺3

⫺2

Figure 3.30

Figure 3.31

3g132⫽ 04

3g1x26 041⫺q, 32 ´ 13, q2

304 CHAPTER 3 Quadratic Functions and Operations on Functions 3–24

College Algebra G&M—

Figure 3.29

WORTHY OF NOTE

Since was a zero of

multiplicity 2, the graph “bounced

off” the x-axis at this point, with no

change of sign for g. The graph is

entirely below the x-axis, except at

the vertex (3, 0).

x ⫽ 3

EXAMPLE 8

䊳

Solving a Quadratic Inequality

Solve the inequality .

Analytical Solution

䊳

Begin by writing the inequality in standard form: . Note this is

equivalent to for . Since , the graph of g will

open downward. The factored form is , showing 3 is a zero and a

repeated root. Using the x-axis, we plot the point (3, 0) and visualize a parabola

opening downward through this point.

Figure 3.29 shows the graph is below the x-axis (outputs are negative) for all

values of x except . But since this is a less than or equal to inequality, the

solution is .

a  0

101234567

x 僆⺢

x ⫽ 3

g1x2⫽⫺1x ⫺ 32

a 6 0g1x2⫽⫺x

⫹ 6x ⫺ 9g1x2ⱕ 0

⫺x

⫹ 6x ⫺ 9 ⱕ 0

⫺x

⫹ 6x ⱕ 9

cob19545_ch03_293-313.qxd 8/10/10 6:07 PM Page 304

Selecting a test value from each interval (in red) gives Figure 3.33:

123

The interval tests show

for , which is

supported by the graph shown in Figure 3.34.

Now try Exercises 133 through 144

䊳

The need to solve a quadratic inequality occurs in a variety of contexts. Here, the

solution is used to ﬁnd the domain of a radical function.

x 僆 1⫺q, ⫺42 ´ 1

, q2

⫺2x

⫺ 3x ⫹ 20 ⱕ 0

1x26 0 inf 1x27 0 inf 1x26 0 in

152⫽⫺45 f 102⫽ 20 f 1⫺52⫽⫺15

x ⫽ 5x ⫽ 0x ⫽ ⫺5

3–25 Section 3.2 Solving Quadratic Equations and Inequalities 305

College Algebra G&M—

⫺15

⫺6

Figure 3.32

1⫺1⫺3 ⫺2⫺4⫺5⫺8 ⫺7 ⫺6 23450 678

12 3

Figure 3.33

Figure 3.34

1⫺1⫺3 ⫺2⫺4⫺5⫺8 ⫺7 ⫺6 23450 678

12 3

1⫺1⫺3 ⫺2⫺4⫺5⫺6 234506

12 3

WORTHY OF NOTE

When evaluating a function using the

interval test method, it’s usually

easier to use the factored form

instead of the polynomial form, since

all you really need is whether the

result will be positive or negative. For

instance, you could likely tell

going to be negative, more

quickly than

.⫺21⫺52

⫺ 31⫺52⫹ 20

f 1⫺52⫽

f 1⫺52⫽⫺321⫺52⫺ 541⫺5 ⫹ 42

EXAMPLE 9

䊳

Solving a Quadratic Inequality

Solve the inequality using interval tests.

Solution

䊳

To begin, we ﬁnd the zeroes of by factoring.

related equation

multiply by ⴚ1

factored form

or zero factor property

or solutions

Plotting these intercepts creates three intervals on the x-axis (Figure 3.32).

x ⫽⫺4x ⫽

x ⫹ 4 ⫽ 02x ⫺ 5 ⫽ 0

12x ⫺ 521x ⫹ 42⫽ 0

2 x

⫹ 3x ⫺ 20 ⫽ 0

⫺2x

⫺ 3x ⫹ 20 ⫽ 0

1x2⫽⫺2x

⫺ 3x ⫹ 20

⫺2x

⫺ 3x ⫹ 20 ⱕ 0

EXAMPLE 10

䊳

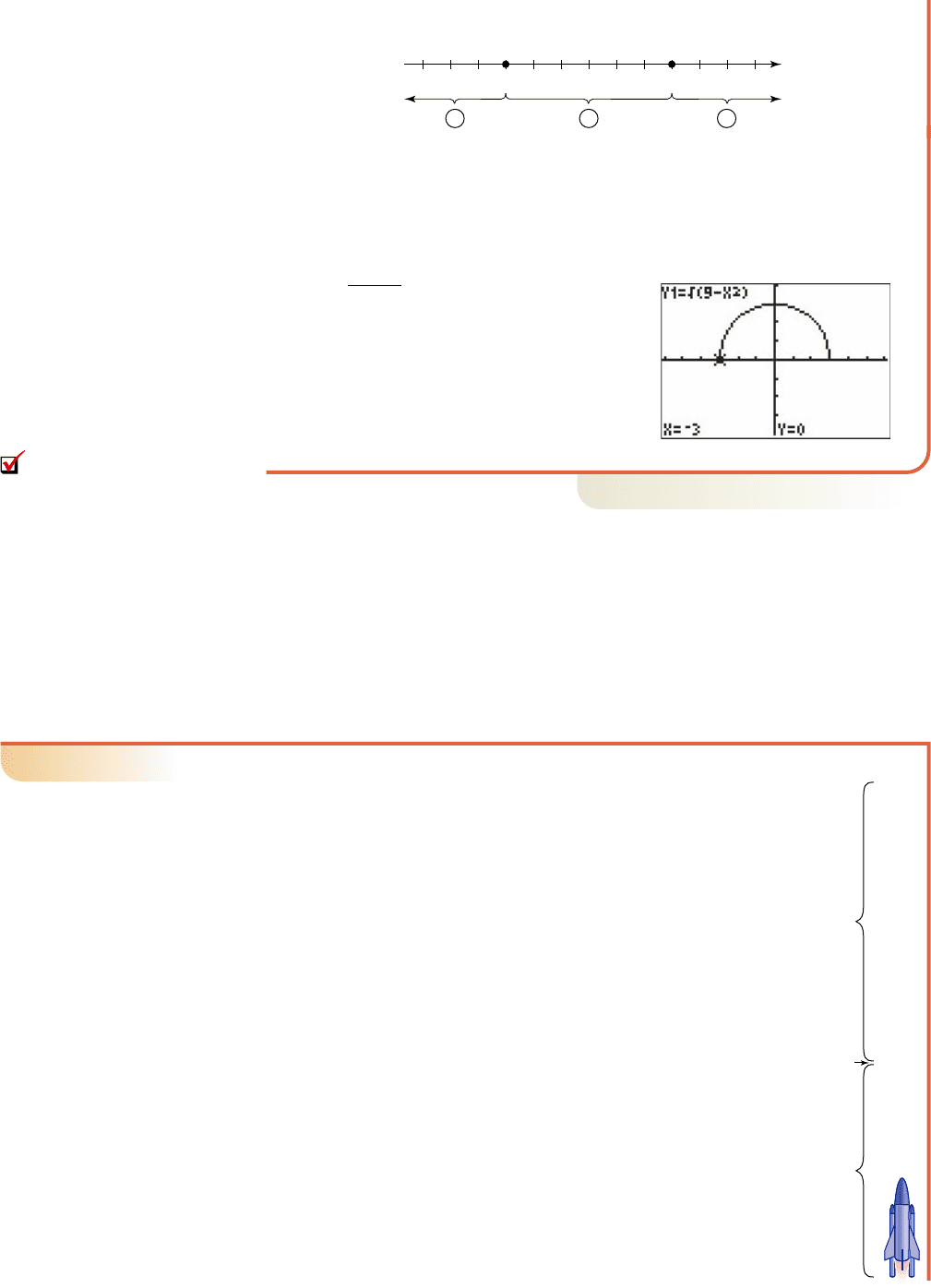
Solving a Quadratic Inequality to Determine the Domain

Find the domain of .

Solution

䊳

From our earlier work, the radicand must be nonnegative and we are essentially

asked to solve the inequality . The related equation is and

by inspection (or factoring), the solutions are and . Plotting these

solutions creates three intervals on the x-axis (Figure 3.35).

x ⫽ 3x ⫽⫺3

9 ⫺ x

⫽ 09 ⫺ x

7 0

g1x2⫽ 29 ⫺ x

Figure 3.35

cob19545_ch03_293-313.qxd 8/10/10 6:07 PM Page 305

306 CHAPTER 3 Quadratic Functions and Operations on Functions 3–26

College Algebra G&M—

F. Applications of Quadratic Functions and Inequalities

A projectile is any object that is thrown, shot, or projected upward with no sustaining

source of propulsion. The height of the projectile at time t is modeled by the equation

where h is the height of the object in feet, t is the elapsed time in

seconds, and v is the initial velocity in feet per second. The constant k represents the

initial height of the object above ground level, as when a person releases an object 5 ft

above the ground in a throwing motion or when a rocket runs out of fuel at an

altitude of 240 ft .

EXAMPLE 11

䊳

Solving an Application of Quadratic Equations—Rocketry

A model rocketry club is testing a newly developed engine. A few

seconds after liftoff, at a velocity of 160 ft/sec and a height of 240 ft,

it runs out of fuel and becomes a projectile (see Figure 3.38).

a. How high is the rocket 3 sec later?

b. For how many seconds was the height of the rocket greater

than or equal to 496 ft?

c. How many seconds until the rocket returns to the ground?

Solution

䊳

a. Using the information given, the function h modeling

the rocket’s height in the projectile phase, is

. For its height at we

have

Three seconds later, the rocket was at an altitude of 576 ft.

⫽ 576

⫽⫺16192⫹ 480 ⫹ 240

h132⫽⫺16132

⫹ 160132⫹ 240

t ⫽ 3h1t2⫽⫺16t

⫹ 160t ⫹ 240

1k ⫽ 2402

1k ⫽ 52,

h ⫽⫺16t

⫹ vt ⫹ k,

Projectile

phase

240 ft

Power

phase

Figure 3.38

1⫺1⫺3 ⫺2⫺4⫺5⫺6234 50 6

12 3

Selecting a test value from each interval (in red) gives Figure 3.36:

123

The interval tests show that for

, which is the domain of

. This is the same relation

we graphed in Section 1.1/Example 3, a

semicircle with endpoints at and 3.

See Figure 3.37.

Now try Exercises 145 through 154

䊳

x ⫽⫺3

g1x2⫽ 29 ⫺ x

x 僆 3⫺3, 34

9 ⫺ x

ⱖ 0

9 ⫺ x

6 0 in9 ⫺ x

7 0 in9 ⫺ x

6 0 in

9 ⫺ 142

⫽⫺79 ⫺ 102

⫽ 99 ⫺ 1⫺42

⫽⫺7

x ⫽ 4x ⫽ 0x ⫽ ⫺4

Figure 3.37

6.1

⫺4

⫺6.1

Figure 3.36

E. You’ve just seen how

we can solve quadratic

inequalities

cob19545_ch03_293-313.qxd 8/10/10 6:07 PM Page 306

b. Since the height h(t) must be greater than or equal to 496 ft, we use the

function to write the inequality

. In standard form, we obtain (subtract

496 from both sides). We begin by ﬁnding the zeroes of ,

noting the related graph opens downward since the leading coefﬁcient is

negative.

related equation

divide by ⴚ16

factor

or zero factor theorem

or result

This shows the rocket is at exactly 496 ft after 2 sec (on its ascent) and after

8 sec (during its descent). We conclude the rocket’s height was greater than

496 ft for 8 ⫺ 2 ⫽ 6 sec.

c. When the rocket hits the ground, its height is . Substituting 0 for and

solving gives

original function

substitute 0 for

(

)

divide by ⴚ16

The equation is nonfactorable, so we use the quadratic equation to solve, with

and :

quadratic formula

substitute 1 for

, ⴚ10 for

, ⴚ15 for

simplify

Since we need the time t in seconds, we

use the approximate form of the answer,

obtaining and . The

rocket will return to the ground in just over

11 sec (since t represents time, the solution

does not apply). A calculator

check is shown in Figure 3.39 using the

Zeroes Method.

Now try Exercises 157 through 166

䊳

EXAMPLE 12

䊳

Solving Applications of Inequalities Using the Quadratic Formula

For the years 1995 to 2006, the amount A of annual international telephone trafﬁc

(in billions of minutes) can be modeled by where

represents the year 1995 [Source: Data from the 2009 Statistical Abstract of

the United States, Table 1344, page 846]. If this trend continues, in what year will

the annual number of minutes reach or surpass 275 billion?

x ⫽ 0

A ⫽ 0.17x

⫹ 8.43x ⫹ 64.58

t ⫽⫺1.32

t ⬇ 11.32t ⬇ ⫺1.32

⫽ 5 ⫾ 2210

2160 ⫽ 4210 ⫽

⫾

4210

⫽

10 ⫾ 2160

⫽

⫺1⫺102⫾ 21⫺102

⫺ 41121⫺152

2112

t ⫽

⫺b ⫾ 2b

⫺ 4ac

c ⫽⫺15a ⫽ 1, b ⫽⫺10,

0 ⫽ t

⫺ 10t ⫺ 15

0 ⫽⫺16t

⫹ 160t ⫹ 240

h1t2⫽⫺16t

⫹ 160t ⫹ 240

h1t2h ⫽ 0

t ⫽ 8 t ⫽ 2

t ⫺ 8 ⫽ 0 t ⫺ 2 ⫽ 0

1t ⫺ 221t ⫺ 82⫽ 0

⫺ 10t ⫹ 16 ⫽ 0

⫺16t

⫹ 160t ⫺ 256 ⫽ 0

⫺16t

⫹ 160t ⫺ 256 ⫽ 0

⫺16t

⫹ 160t ⫺ 256 ⱖ 0240 ⱖ 496

⫺16t

⫹ 160t ⫹h1t2⫽⫺16t

⫹ 160t ⫹ 240

3–27 Section 3.2 Solving Quadratic Equations and Inequalities 307

College Algebra G&M—

800

⫺200

Figure 3.39

cob19545_ch03_293-313.qxd 8/10/10 6:08 PM Page 307

Analytical Solution

䊳

We are essentially asked to solve the inequality

given inequality

subtract 275

For and the quadratic formula gives

quadratic formula

substitute known values

simplify

or result

We disregard the negative solution (since x represents time), and ﬁnd the annual

number of international telephone minutes will reach or surpass 275 billion about

18 years after 1995, or in the year 2013.

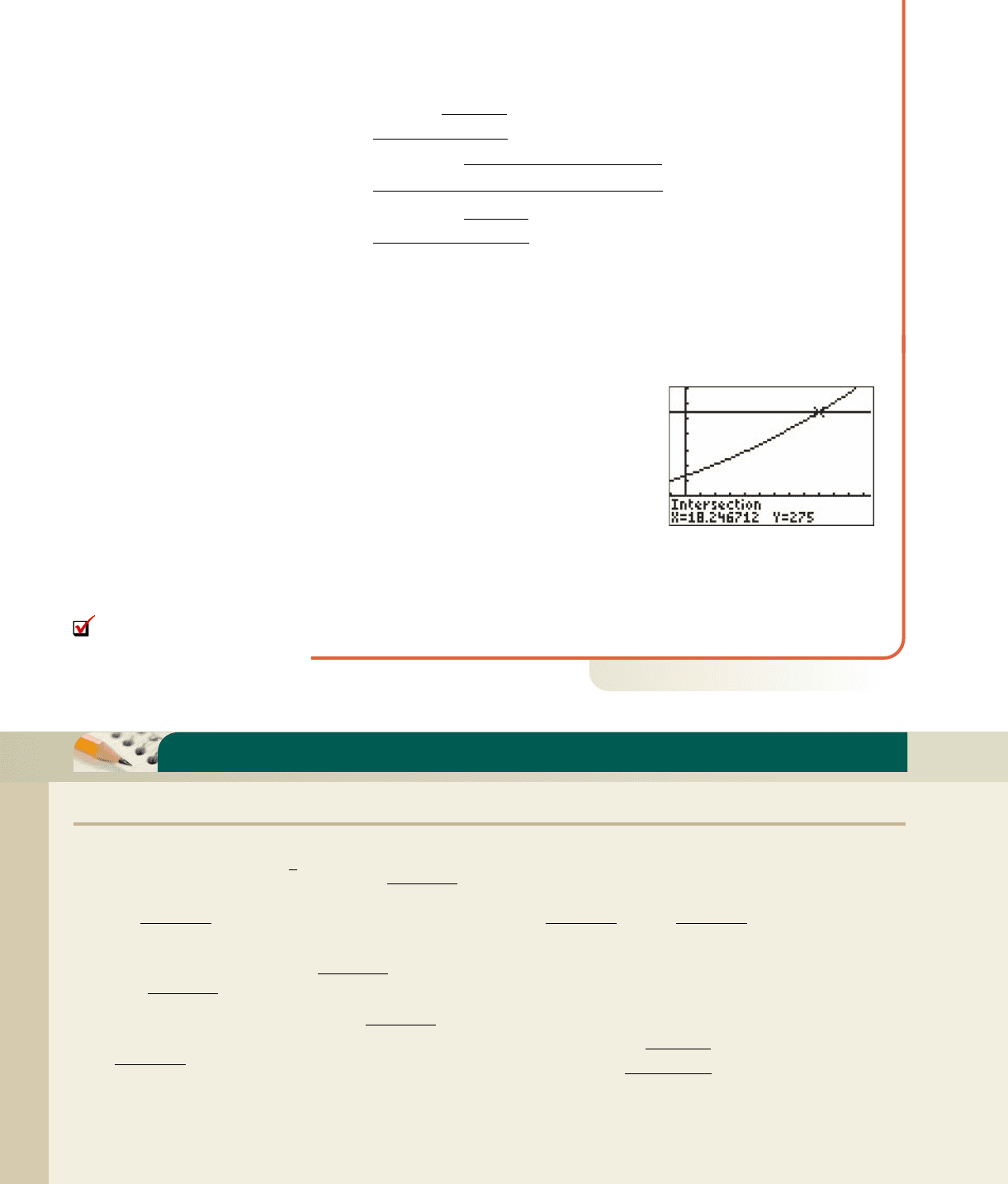
Graphical Solution

䊳

After entering as Y

our next task is to determine an appropriate

window size. With 1995 as year and the

data taken from year 2006 it seems

that to would be an

appropriate start for the domain (we can later

adjust the window if needed). As the primary

question is the year when telephone trafﬁc

surpasses 275 billion minutes, the range must

include this value and to

would be a good start (as before, the negative values were used to create a frame

around the desired window). Using the Intersection-of-Graphs method, the resulting

graph is shown in the ﬁgure and indicates that telephone trafﬁc surpassed 275

billion minutes in the 18th year (2013), in line with our analytical solution.

Now try Exercises 167 and 168

䊳

y ⫽ 350y ⫽⫺100

x ⫽ 25x ⫽⫺2

1x ⫽ 112

x ⫽ 0

0.17x

⫹ 8.43x ⫹ 64.58

x ⬇ ⫺67.83x ⬇ 18.25

x ⫽

⫺8.43 ⫾ 2214.1505

0.34

x ⫽

⫺8.43 ⫾ 218.432

⫺ 410.1721⫺210.422

210.172

x ⫽

⫺b ⫾ 2b

⫺ 4ac

c ⫽⫺210.42,a ⫽ 0.17, b ⫽ 8.43,

ⱖ 00.17x

⫹ 8.43x ⫺ 210.42

ⱖ 2750.17x

⫹ 8.43x ⫹ 64.58

ⱖ 275.0.17x

⫹ 8.43x ⫹ 64.58

308 CHAPTER 3 Quadratic Functions and Operations on Functions 3–28

College Algebra G&M—

F. You’ve just seen how

we can solve applications of

quadratic functions and

inequalities

350

⫺100

⫺2

4. According to the summary on page 22, the

equation might best be solved by

out the .

⫺ 5x

䊳

CONCEPTS AND VOCABULARY

Fill in each blank with the appropriate word or phrase. Carefully reread the section, if necessary.

3.2 EXERCISES

1. The solution is called an

form of the solution. Using a calculator, we ﬁnd

the form is x ⬇ 3.732.

x ⫽ 2 ⫹ 13

2. To solve a quadratic equation by completing the

square, the coefﬁcient of the term must

be a .

5. Discuss/Explain the relationship between solutions

to and the x-intercepts of . Be

sure to include an example.

y ⫽ f

1x2f 1x2⫽ 0

3. The quantity is called the of

the quadratic equation. If there are

real roots.

⫺ 4ac 7 0,

⫺ 4ac

6. Discuss/Explain why this version of the quadratic

formula is incorrect:

x ⫽⫺b ⫾

⫺ 4ac

cob19545_ch03_293-313.qxd 11/25/10 3:29 PM Page 308

3–29 Section 3.2 Solving Quadratic Equations and Inequalities 309

College Algebra G&M—

Solve by completing the square. Write your answers in

both exact form and approximate form rounded to the

hundredths place. If there are no real solutions, so state.

43. 44.

45. 46.

47. 48.

49. 50.

51. 52.

Solve the following quadratic equations (a) algebraically

by completing the square and (b) graphically by using a

graphing calculator and the Zeroes Method. Round

answers to nearest hundredth when necessary.

53. 54.

55. 56.

57. 58.

59. 60.

Solve each equation using the most efﬁcient method:

factoring, square root property of equality, or the

quadratic formula. Write your answer in both exact and

approximate form (rounded to hundredths). Check one

of the exact solutions in the original equation.

61. 62.

63. 64.

65. 66.

67. 68.

69. 70.

71. 72.

73. 74.

75. 76.

77. 78.

79. 80. 3m

⫺ 2 ⫽ 5m5w

⫺ w ⫽ 1

⫹ x ⫹ 3 ⫽ 05p

⫽ 6p ⫹ 3

⫺ 2n ⫺ 3 ⫽ 03a

⫺ a ⫹ 2 ⫽ 0

⫺ 7m ⫺ 6 ⫽ 05w

⫽ 6w ⫹ 8

⫺ x ⫽ 34n

⫺ 9 ⫽ 0

⫹ p ⫽ 04m

⫽ 12m ⫺ 15

⫺ 5a ⫹ 6 ⫽ 06w

⫺ w ⫽ 2

⫺ 4x ⫹ 5 ⫽ 04n

⫺ 8n ⫺ 1 ⫽ 0

⫺ 4a ⫽ 14m

⫺ 25 ⫽ 0

⫹ 6w ⫺ 1 ⫽ 0x

⫺ 3x ⫽ 18

⫺ 15 ⫽ 4am

⫽ 7m ⫺ 4

⫹ 5x ⫺ 6 ⫽ 04p

⫺ 3p ⫺ 2 ⫽ 0

⫺ 5p ⫽ 12n

⫺ 3n ⫺ 9 ⫽ 0

⫺ 8w ⫹ 4 ⫽ 02x

⫽⫺7x ⫹ 4

⫺ 7w ⫹ 3 ⫽ 0n

⫽ 5n ⫹ 5

⫹ 5n ⫺ 2 ⫽ 0m

⫹ 3m ⫽ 1

⫺ 8x ⫺ 1 ⫽ 0p

⫹ 6p ⫽⫺4

⫽ 4n ⫹ 10p

⫺ 6p ⫹ 3 ⫽ 0

⫹ 8m ⫽⫺12x

⫹ 6x ⫽⫺5

Solve the following equations graphically by locating the

zeroes of a related quadratic function. Round to

hundredths as necessary.

13.

14.

15.

16.

17.

18.

19.

20.

Solve the following equations using the square root

property of equality. Write answers in exact form

and approximate form rounded to hundredths. If

there are no real solutions, so state. Verify solutions

graphically.

21. 22.

23. 24.

25. 26.

27. 28.

29. 30.

31. 32.

33. 34.

35. 36.

Fill in the blank so the result is a perfect square

trinomial, then factor into a binomial square.

37. 38.

39. 40.

41. 42. x

⫺

x ⫹

_______

⫹

p ⫹

_______

⫺ 5x ⫹

_______

⫹ 3n ⫹

_______

⫹ 10y ⫹

_______

⫹ 6x ⫹

_______

1x ⫺ 52

⫽

1m ⫺ 22

⫽

1m ⫹ 112

⫹ 5 ⫽ 31x ⫺ 32

⫹ 7 ⫽ 2

1m ⫺ 42

⫽ 51w ⫹ 52

⫽ 3

1p ⫹ 52

⫽ 491n ⫺ 32

⫽ 36

⫽

⫹ 5 ⫽ 0p

⫹ 36 ⫽ 0

⫺ 20 ⫽ 0y

⫺ 28 ⫽ 0

⫽ 49m

⫽ 16

8.1x

⫽ 5.3x ⫺ 4.2

2.9x

⫽ 1.3x ⫺ 5.7

⫹ x ⫽ 3

⫺ 3x ⫽ 6

⫹ 0.2x ⫺ 1.1 ⫽ 0

0.4x

⫺ 0.6x ⫺ 2 ⫽ 0

⫺ 7x ⫺ 2 ⫽ 0

⫹ 3x ⫺ 5 ⫽ 0

䊳

DEVELOPING YOUR SKILLS

,, ,

;; ;

,, ,

7. 8. 9.

10. 11. 12. 2x

⫹ 4x ⫽ 64x

⫽ 4x ⫹ 83x

⫹ 8x ⫽ 3

⫹ x ⫽ 3x

⫺ 4x ⫺ 5 ⫽ 0x

⫹ x ⫺ 12 ⫽ 0

l1⫺32⫽ l1

2⫽ 0k1

⫺3

2⫽ k112⫽ 0;j1⫺12⫽ j122⫽ 0;

l1x2⫽ 3x

⫹ 8x ⫺ 3k1x2⫽ 2x

⫹ x ⫺ 3j1x2⫽⫺4x

⫹ 4x ⫹ 8

h1⫺32⫽ h112⫽ 0g1⫺12⫽ g152⫽ 0f

1⫺42⫽ f 132⫽ 0

h1x2⫽⫺2x

⫺ 4x ⫹ 6g1x2⫽ x

⫺ 4x ⫺ 5f 1x2⫽ x

⫹ x ⫺ 12

Six functions are shown below, along with their respective zeroes. Use these zeroes to solve the equations in Exercises

7 through 12.

cob19545_ch03_293-313.qxd 8/10/10 6:08 PM Page 309