Coburn J.W., Herdlick J.D. College Algebra: Graphs and Models

Подождите немного. Документ загружается.

330 CHAPTER 3 Quadratic Functions and Operations on Functions 3–50

College Algebra G&M—

Applications of quadratic regression tend to focus on the deﬁning characteristics of

a quadratic graph, even if only a part of the graph is used. The data may simply indicate

an increasing rate of growth beyond an initial or minimum point as in Example 1, or

show values that decrease to a minimum and increase afterward. These would be data

sets modeled by an equation where . Applications where are also common.

In actual practice, data sets are often very large and need not be integer-valued.

In addition, as we explore additional functions and forms of regression, the decision

of which form to use must be carefully evaluated as many functions exhibit similar

characteristics.

EXAMPLE 2

䊳

Apollo 13, Retro-Rocket Option

About 56 hr into the mission and 65,400 km from the Moon, the

oxygen tanks exploded on Apollo 13. At this point, mission control

explored two options: (1) ﬁring the retro-rockets for a direct return

to Earth, or (2) the so called, “sling-shot around the Moon,” the

option actually chosen. The data shown in the table explore a

scenario where option 1 was taken, and give the distance d from

the Moon, t seconds after the retro-rockets have ﬁred.

a. Input the data into a graphing calculator, set an

appropriate window and view the scatterplot,

then use the context and the scatterplot to decide

on an appropriate form of regression.

b. Determine the regression equation, and use it to

ﬁnd how close Apollo 13 would have come to the

Moon (the minimum distance). How many

seconds after the retro-rockets ﬁred would this

have occurred?

c. How many seconds would it have taken for

Apollo 13 to “turn around,” and get back to

the original distance of 65,400 km (where the

accident occurred)?

Solution

䊳

a. After entering the data (seconds in L1 and

distance in L2), we set a viewing window

of , , and after some

trial and error, , and

. The scatterplot shows

(be sure that is activated on the

screen) a gradually decreasing,

nonlinear pattern and a quadratic regression

seems appropriate (Figure 3.58).

b. We ﬁnd the regression equation

using (CALC) 5:QuadReg

(pasting the equation to Y

Next, press to obtain the graph and

scatterplot shown in Figure 3.59. The

result indicates that we should increase

the value of Xmax to see the full graph and

to help locate the minimum value. Using

and the (CALC)

3:minimum option shows that Apollo 13

would have come within 65,328.5 km of the

Moon, after the retro-rockets had ﬁred for

12.4 sec (Figure 3.60).

TRACE

2nd

Xmax ⫽ 30

GRAPH

⬇ 0.464X

⫺ 11.519X ⫹ 65,400.013

STAT

PLOT1

Ymax ⫽ 65,450

Ymin ⫽ 65,300

Xmax ⫽ 15Xmin ⫽ 0

a 6 0a 7 0

Time Distance from

(sec) Moon (km)

0 65,400

1 65,389.0

2 65,378.8

3 65,369.6

4 65,361.4

5 65,354.0

10 65,331.2

65,450

65,300

Figure 3.58

65,450

65,300

Figure 3.59

cob19545_ch03_329-339.qxd 8/10/10 8:26 PM Page 330

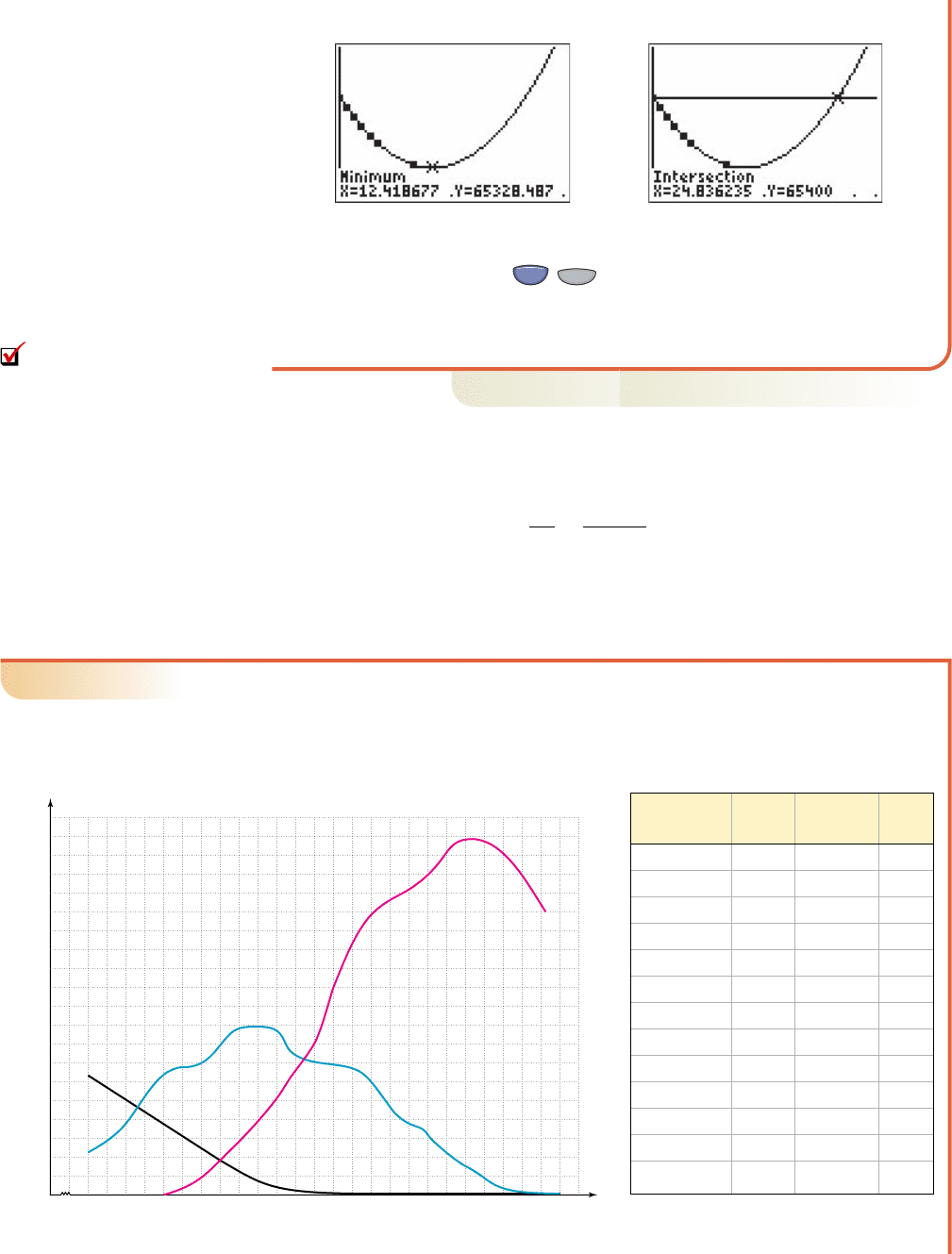
c. For the time required to return to a distance of 65,400 km, we enter

and use the (CALC) 5:intersect option. The result

shown in Figure 3.61 indicates a required time of about 25 sec. Actually, we

could have reasoned that if it took 12.5 sec to reach the minimum distance, we

could double this time to return to the original distance.

Now try Exercises 11 through 14 and 45 through 48

䊳

B. Nonlinear Functions and Rates of Change

As noted in Section 1.2, one of the deﬁning characteristics of linear functions is that

their rate of change is constant: . For nonlinear functions the rate

of change is not constant, but to aid in their study and application, we use a related con-

cept called the average rate of change, given by the slope of a secant line through

points (x

, y

) and (x

, y

) on the graph.

EXAMPLE 3

䊳

Calculating Average Rates of Change

The graph shown displays the number of units shipped of vinyl records, cassette

tapes, and CDs for the period 1980 to 2005.

¢y

¢x

⫽

⫺ y

⫺ x

⫽ m

TRACE

2nd

⫽ 65,400

3–51 Section 3.4 Quadratic Models; More on Rates of Change 331

College Algebra G&M—

65,450

65,300

Figure 3.60

65,450

65,300

Figure 3.61

A. You’ve just seen how

we can develop quadratic

function models from a set

of data

100

200

300

400

1000

Units shipped (millions)

6810

Cassettes

Vinyl

CDs

12 14 16 18 20 22 24 26

500

600

700

800

900

Year (1980 → 0)

Source: Swivel.com

Units shipped in millions

Year

(1980 S 0) Vinyl Cassette CDs

0 323 110 0

2 244 182 0

4 205 332 6

6 125 345 53

8 72 450 150

10 12 442 287

12 2 366 408

14 2 345 662

16 3 225 779

18 3 159 847

20 2 76 942

24 1 5 767

25 1 3 705

cob19545_ch03_329-339.qxd 8/10/10 8:26 PM Page 331

a. Find the average rate of change in CDs shipped and in cassettes shipped from

1994 to 1998. What do you notice?

b. Does it appear that the rate of increase in CDs shipped was greater from 1986

to 1992, or from 1992 to 1996? Compute the average rate of change for each

period and comment on what you ﬁnd.

Solution

䊳

Using 1980 as year zero ( ), we have the following:

a. CDs Cassettes

The decrease in the number of cassettes shipped was roughly equal to the

increase in the number of CDs shipped (about 46,000,000 per year).

b. From the graph, the secant line for 1992 to 1996 appears to have a greater

slope.

1986–1992 CDs 1992–1996 CDs

For the years 1986 to 1992, the average rate of change for CD sales was about

59.2 million per year. For the years 1992 to 1996, the average rate of change

was almost 93 million per year, a signiﬁcantly higher rate of growth.

Now try Exercises 15 through 26, 49 and 50

䊳

C. The Average Rate of Change Formula

The importance of the rate of change concept would be hard to overstate. In many busi-

ness, scientiﬁc, and economic applications, it is this attribute of a function that draws the

most attention. In Example 3 we computed average rates of change by selecting two

points from a graph, and computing the slope of the secant line: .

With a simple change of notation, we can use the function’s equation rather than relying

on a graph. Note that y

corresponds to the function evaluated at x

: . Likewise,

. Substituting these into the slope formula yields , giving

the average rate of change between x

and x

for any function f.

Average Rate of Change

For a function f and [x

, x

] a subset of the domain,

the average rate of change between x

and x

¢y

¢x

⫽

2⫺ f 1x

⫺ x

, x

⫽ x

¢y

¢x

⫽

2⫺ f 1x

⫺ x

⫽ f 1x

m ⫽

¢y

¢x

⫽

⫺ y

⫺ x

⫽ 92.75 ⫽ 59.16

⫽

371

⫽

355

¢y

¢x

⫽

779 ⫺ 16

16 ⫺ 12

¢y

¢x

⫽

408 ⫺ 53

12 ⫺ 6

1992: 112, 4082, 1996: 116, 77921986: 16, 532, 1992: 112, 4082

⫽⫺46.5 ⫽ 46.25

⫽⫺

186

⫽

185

¢y

¢x

⫽

159 ⫺ 345

18 ⫺ 14

¢y

¢x

⫽

847 ⫺ 662

18 ⫺ 14

1994: 114, 3452, 1998: 118, 15921994: 114, 6622, 1998: 118, 8472

1980 S 0

332 CHAPTER 3 Quadratic Functions and Operations on Functions 3–52

College Algebra G&M—

B. You’ve just seen how

we can calculate the average

rate of change for nonlinear

functions using points on a

graph

cob19545_ch03_329-339.qxd 8/10/10 8:26 PM Page 332

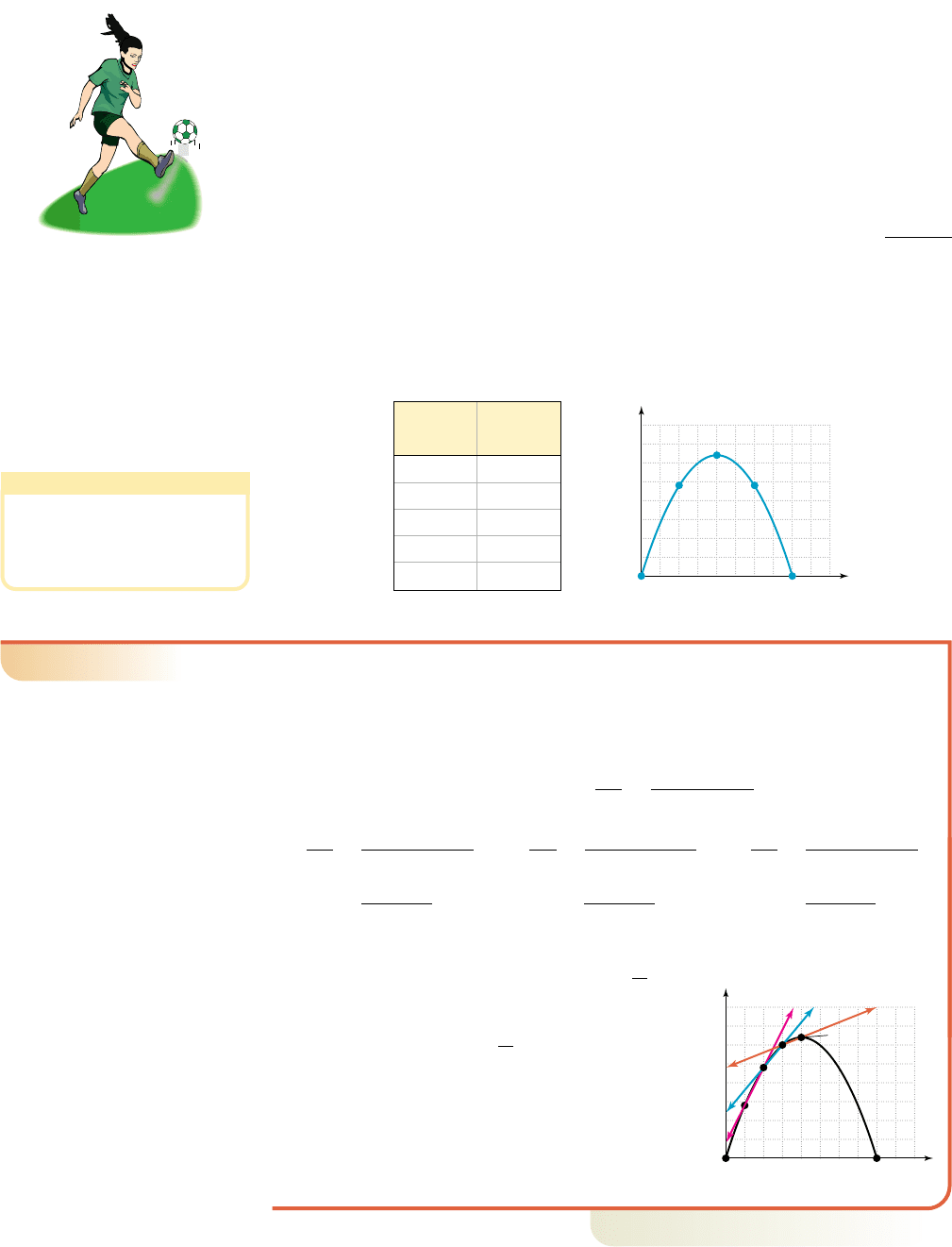
Average Rates of Change Applied to Projectile Velocity

A projectile is any object that is thrown, shot, or cast upward, with no continuing

source of propulsion. The object’s height (in feet) after t sec is modeled by the function

, where v is the initial velocity of the projectile, and k is the

height of the object at . For instance, if a soccer ball is kicked vertically upward

from ground level ( ) with an initial speed of 64 ft/sec, the height of the ball t sec

later is . From Section 3.3, we recognize the graph will be a

parabola and evaluating the function for to 4 produces Table 3.1 and the graph

shown in Figure 3.62. Experience tells us the ball is traveling at a faster rate immedi-

ately after being kicked, as compared to when it nears its maximum height where it

momentarily stops, then begins its descent. In other words, the rate of change

has a larger value at any time prior to reaching its maximum height. To quantify this

we’ll compute the average rate of change between (a) and , and compare

it to the average rates of change between, (b) and , and (c) and

.t ⫽ 2

t ⫽ 1.5t ⫽ 1.5t ⫽ 1

t ⫽ 1t ⫽ 0.5

¢height

¢time

t ⫽ 0

h1t2⫽⫺16t

⫹ 64t

k ⫽ 0

t ⫽ 0

h1t2⫽⫺16t

⫹ vt ⫹ k

3–53 Section 3.4 Quadratic Models; More on Rates of Change 333

College Algebra G&M—

Figure 3.62

(1, 48)

(3, 48)

(2, 64)

h(t)

12345

Table 3.1

EXAMPLE 4

䊳

Average Rates of Change Applied to Projectiles

For the projectile function , ﬁnd the average rate of change for

a. . b. . c. .

Then graph the secant lines representing these average rates of change and comment.

Solution

䊳

Using the given intervals in the formula yields

a. b. c.

For , the average rate of change is

meaning the height of the ball is increasing at an

average rate of 40 ft/sec. For , the average

rate of change has slowed to , and the soccer ball’s

height is increasing at only 24 ft/sec. In the interval

[1.5, 2], the average rate of change has slowed to

8 ft/sec. The secant lines representing these rates of

change are shown in the ﬁgure, where we note the line

from the ﬁrst interval (in red), has a much steeper

slope than the line from the third interval (in gold).

Now try Exercises 27 through 34

䊳

t 僆 31, 1.54

,t 僆 30.5, 14

⫽ 8 ⫽ 24 ⫽ 40

⫽

64 ⫺ 60

0.5

⫽

60 ⫺ 48

0.5

⫽

48 ⫺ 28

0.5

¢h

¢t

⫽

h122⫺ h11.52

2 ⫺ 1.5

¢h

¢t

⫽

h11.52⫺ h112

1.5 ⫺ 1

¢h

¢t

⫽

h112⫺ h10.52

1 ⫺ 10.52

¢h

¢t

⫽

h1t

2⫺ h1t

⫺ t

t 僆 31.5, 2.04t 僆 31, 1.54t 僆 30.5, 14

h1t2⫽⫺16t

⫹ 64t

WORTHY OF NOTE

Keep in mind the graph of h

represents the relationship between

the soccer ball’s height in feet and

the elapsed time t. It does not

model the actual path of the ball.

(0, 0)

(0.5, 28)

(1.5, 60)

(2, 64)

(4, 0)

(1, 48)

h(t)

12345

Time in Height in

seconds feet

148

264

348

cob19545_ch03_329-339.qxd 8/10/10 8:26 PM Page 333

The calculation for average rates of change can be applied to any function

and will yield valuable information—particulary in an applied context. For practice

with other functions, see Exercises 35 to 42.

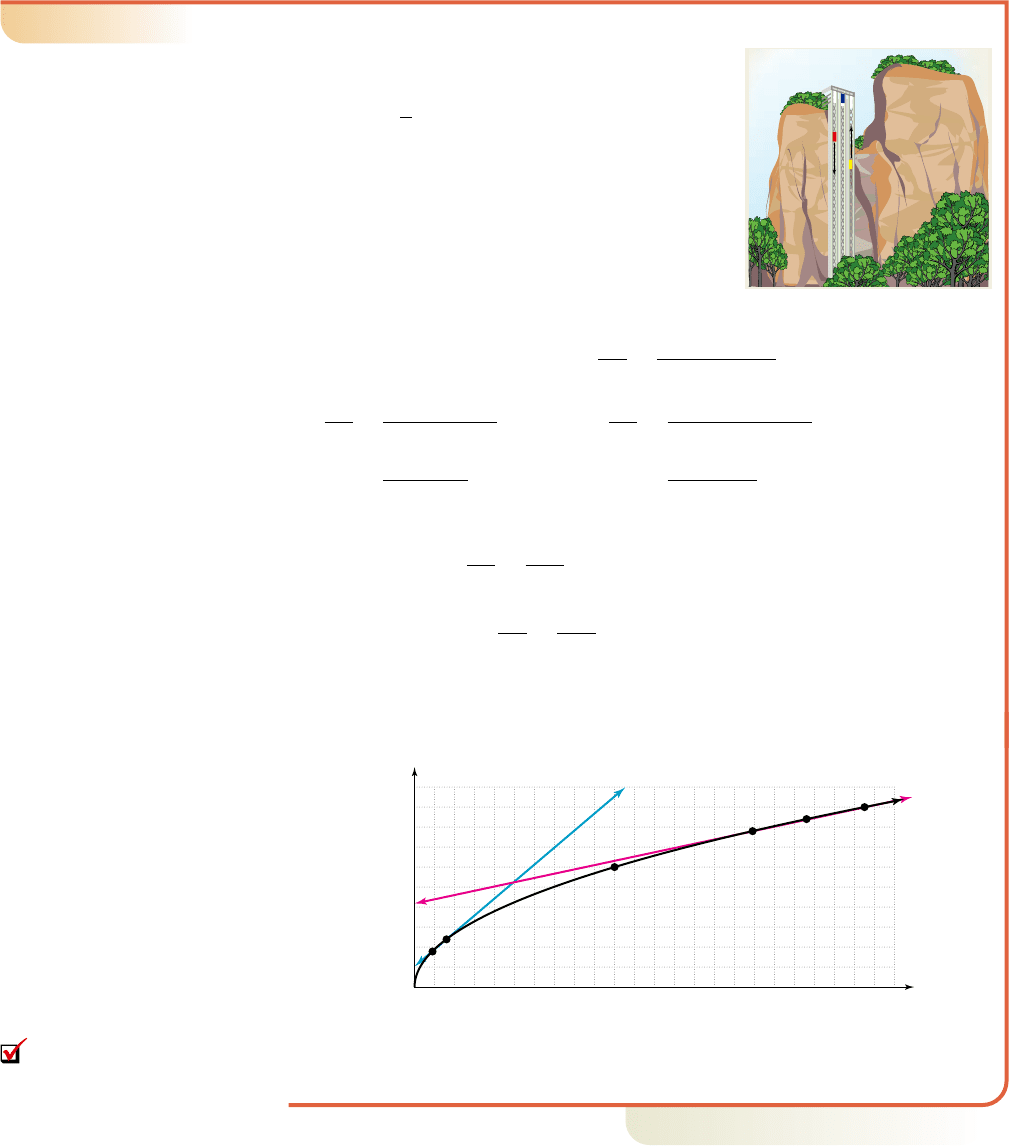
You may have had the experience of riding in the external elevator of a modern

building, with a superb view of the surrounding area as you rise from the bottom ﬂoor.

For the ﬁrst few ﬂoors, you note you can see much farther than from ground level. As

you ride to the higher ﬂoors, you can see still farther, but not that much farther due to

the curvature of the Earth. This is another example of a nonconstant rate of change.

EXAMPLE 5

䊳

Average Rates of Change Applied to Viewing Distance

The distance a person can see depends their elevation

above level ground. On a clear day, this viewing

distance can be approximated by the function

, where d(h) represents the viewing

distance (in miles) at height h (in feet) above level

ground. Find the average rate of change to the

nearest 100th, for

c. Graph the function along with the lines

representing the average rate of change and comment on what you notice.

Solution

䊳

Use the points given in the formula:

a. b.

c. For , meaning the viewing distance is increasing at an

average rate of 0.17 miles (about 898 feet) for each 1 ft increase in elevation.

For and the viewing distance is increasing at a rate

of only 0.04 miles (about 211 feet) for each increase of 1 ft. We’ll sketch the

graph using the points (0, 0), (9, 3.6), (16, 4.8), (196, 16.8) and (225, 18),

along with (100, 12) and (169, 15.6) to help round out the graph (Figure 3.63).

Note the slope of the secant line through the points (9, 3.6) and (16, 4.8), has a

much steeper slope than the line through (196, 16.8) and (225, 18).

Now try Exercises 51 through 56

䊳

Height

Viewing distance

20 40 60 80 100 120 140 160 240180

200 220

(9, 3.6)

(100, 12)

(169, 15.6)

(225, 18)

(196, 16.8)

(16, 4.8)

h 僆 3196, 2254,

¢d

¢h

⬇

0.04

h 僆 39, 164,

¢d

¢h

⬇

0.17

⬇ 0.04 ⬇ 0.17

⫽

18 ⫺ 16.8

⫽

4.8 ⫺ 3.6

¢d

¢h

⫽

d12252⫺ d11962

225 ⫺ 196

¢d

¢h

⫽

d1162⫺ d192

16 ⫺ 9

¢d

¢h

⫽

d1h

2⫺ d1h

⫺ h

h 僆 3196, 2254

h 僆 39, 164

d1h2⫽ 1.21h

y ⫽ f 1x2

334 CHAPTER 3 Quadratic Functions and Operations on Functions 3–54

College Algebra G&M—

C. You’ve just seen how

we can calculate average rates

of change using the average

rate of change formula

Figure 3.63

cob19545_ch03_329-339.qxd 11/25/10 3:36 PM Page 334

3.4 EXERCISES

2. For linear functions, the rate of change is

. For functions, the rate of

change is not constant.

䊳

CONCEPTS AND VOCABULARY

Fill in each blank with the appropriate word or phrase. Carefully reread the section if needed.

1. Data that indicate a gradual increase to a maximum

value, matched by a like decrease, might best be

modeled using regression. In the case

described, the coefﬁcient of the x

-term will be

3. The rate of change of a function can be

found by calculating the of the line that

passes through two points on the graph of the

function. For nonlinear functions, this is called

a .

4. The average rate of change of a function f(x)

between x

and x

is given by the formula

. To avoid division by , x

cannot equal x

5. Discuss/Explain the differences between the three

types of regressions we have studied so far (linear,

power, and quadratic). Include examples that

highlight the different behavior of each of these

types of models.

6. Given , compare the average rate

of change near the vertex, with on either side

of the vertex. Include speciﬁc intervals and values

in your discussion.

¢y

¢x

1x2⫽ 2x

⫺ 12x

3–55 Section 3.4 Quadratic Models; More on Rates of Change 335

College Algebra G&M—

䊳

DEVELOPING YOUR SKILLS

Use a graphing calculator and the tables shown to ﬁnd

(a) a quadratic regression equation that models the

data, (b) the output of the function for , and

nearest thousandths as necessary.

7. 8.

9. 10.

x ⴝ 3.5

Use a graphing calculator and the tables shown to ﬁnd

(a) a quadratic regression equation y ⫽ f(x) that models

the data, (b) the value of f(x) at the vertex, and (c) the

two values of x where f(x) ⫽ 25. Round to nearest

thousandths.

11. 12.

13. 14.

3 0.73

5 18.75

7 48.37

8 67.53

⫺5.69

1 67.8

2 63.4

3 68.5

4 67.7

5 55.1

6 51.7

7 47.3

8 31.4

9 27.2

10 9.9

6 3.2

7 27.2

8 42.6

9 88.4

10 105.3

⫺5.1

⫺17.5

⫺14.2

⫺13.9

⫺1.0

0 67.6

5 29.6

10 9.9

15 3.3

35 4.6

40 6.8

45 25.7

50 54.8

⫺7.9

⫺17.1

⫺8.2

10 30.4

20 50.1

30 56.7

40 76.5

50 71.9

60 73.6

70 55.4

80 53.2

90 19.3

100 5.2

⫺7.6

1 4.29

2 10.72

4 37.74

5 58.33

7 113.67

1 37.8

3 12.1

5 15.3

6 28.2

8 71.9

7 8.5

8 98.6

⫺59.3

⫺66.2

⫺48.7

cob19545_ch03_329-339.qxd 11/25/10 3:37 PM Page 335

Using the graphs shown, ﬁnd the average rate of change

of f and g for the intervals speciﬁed.

15.

16.

17.

18.

19.

20.

21.

22.

23.

24.

25.

26.

The functions shown are projectile equations where h(t)

is the height of the projectile after t sec. Calculate

over the intervals indicated. Include units of measurement

in your answer.

27. , h in feet

a. [2, 5] b. [3, 5]

c. [4, 5] d. [5, 7]

28. , h in feet

a. [0.25, 1] b. [0.5, 1]

c. [0.75, 1] d. [1, 1.5]

29. , h in meters

a. [1, 6] b. [2, 5]

c. [2.5, 3.5] d. [3.5, 4.5]

30. , h in meters

a. [1, 2] b. [0.2, 2.8]

c. [0.5, 1.5] d. [1.5, 2.5]

h1t2⫽⫺4.9t

⫹ 14.7t ⫹ 4.1

h1t2⫽⫺4.9t

⫹ 34.3t ⫹ 2.6

h1t2⫽⫺16t

⫹ 32t

h1t2⫽⫺16t

⫹ 160t

¢h

¢t

g1x2 for x 僆 30, 54

g1x2 for x 僆 3⫺3, 54

g1x2 for x 僆 30, 44

g1x2 for x 僆 3⫺3, 44

g1x2 for x 僆 30, 14

g1x2 for x 僆 3⫺3, 14

1x2 for x 僆 3⫺3, ⫺14

1x2 for x 僆 3⫺5, ⫺34

1x2 for x 僆 3⫺3, 24

1x2 for x 僆 32, 64

1x2 for x 僆 3⫺1, 44

1x2 for x 僆 3⫺5, ⫺14

(6, 4.1)

(4, 0.9)

(2, ⫺1.5)

(⫺1, ⫺3.6)

(⫺3, ⫺4)

(⫺5, ⫺3.6)

7⫺6

⫺5

f(x)

(5, 13.5)

(4, 3.2)

(0, 0)

(⫺3, 3.9)

(⫺5, ⫺8.5)

(1, ⫺2.5)

6⫺6

⫺10

⫺5

g(x)

Graph the function and secant lines representing the

average rates of change for the exercises given. Comment

on what you notice in terms of the projectile’s velocity.

31. Exercise 27.

32. Exercise 28.

33. Exercise 29.

34. Exercise 30.

Graph each function in an appropriate window, then

ﬁnd the average rate of change for the interval speciﬁed.

Round to hundredths as needed.

35.

36.

37.

38.

39. ; [70, 100]

40. ; [1.3, 1.5]

41. ; [5, 7]

42. ; [5, 7]V ⫽

␲r

A ⫽ ␲r

␳ ⫽ 0.2m

F ⫽ 9.8m

y ⫽

冟

3x ⫹ 1

冟

⫺2; 3⫺2, 24

y ⫽ 2

冟

x ⫹ 3

冟

; 3⫺4, 04

y ⫽ 2

x ⫹ 5; 3⫺5, 34

y ⫽ x

⫺ 8; 32, 54

2.521.510.5

3.53

642

1357

1.510.5

87654321

109

100

150

200

250

300

350

400

450

500

336 CHAPTER 3 Quadratic Functions and Operations on Functions 3–56

College Algebra G&M—

cob19545_ch03_329-339.qxd 8/12/10 8:14 PM Page 336

3–57 Section 3.4 Quadratic Models; More on Rates of Change 337

College Algebra G&M—

䊳

WORKING WITH FORMULAS

43. Height of a falling object:

Neglecting air resistance, the height of an object

that is thrown straight downward with velocity v

from a height of h

is given by the formula shown,

where h(t) represents the height at time t. The

Earth’s longest vertical drop (on land) is the Rupal

Face on Nanga Parbat (Pakistan), which rises

15,000 ft above its base. From the top of this rock

face, a climber’s piton hammer slips from her hand

and is projected downward with an initial velocity

of 6 ft/sec. Determine the hammer’s height after

(a) sec and (b) sec. (c) Use the results

to calculate the average rate of change over this

t ⫽ 7t ⫽ 5

h1t2ⴝⴚ16t

ⴚ v

t ⴙ h

2-sec interval. (d) Repeat parts a, b, and c for

sec and sec and comment.

44. The Difference Quotient:

As we’ll see in Section 3.6, the difference quotient

is closely related to the average rate of change.

a. Given and , evaluate D(3)

using the formula.

b. Calculate the average rate of change of f(x)

over the interval [3, 3.1] and comment on what

you notice.

h ⫽ 0.1f

1x2⫽ x

D1x2ⴝ

1x ⴙ h2ⴚ f 1x2

t ⫽ 12t ⫽ 10

䊳

APPLICATIONS

45. Registration for 5-km

race: A local community

hosts a popular 5-km race

to raise money for breast

cancer research. Due to

certain legal restrictions,

only the ﬁrst 5000

registrants will be allowed

to compete. The table

shows the cumulative number of registered

participants at the end of the day, for the ﬁrst

5 days. (a) Use a graphing calculator to ﬁnd a

quadratic regression equation that models the data.

Use this equation to estimate (b) the number of

participants after 1 week of registration, (c) the

number of days it will take for the race to ﬁll up,

and (d) the maximum number of participants that

would have signed up had there been no limit.

Round to the nearest hundredth when necessary.

46. Concert tickets: In San

Francisco, the Javier

Mendoza Band has

scheduled a concert at

Candlestick Park. Once

the tickets go on sale, the

band is sure to sell out

this 70,000 person venue.

The table shows the cumulative number of tickets

sold each week, for the ﬁrst 4 weeks. (a) Use a

graphing calculator to ﬁnd a quadratic regression

equation that models the data. Use this equation to

(b) estimate the number of tickets sold after 5 weeks,

the concert to sell out, and (d) estimate the number

of fans that won’t get to attend the show.

47. Guided tours: A tour

guide for Kalaniohana

Tours noticed that for

groups of two to seven

people, the average time

it took to organize them at

the beginning of a tour

actually decreased as the

group size increased. For

groups of eight or more,

however, the logistics (and questions asked)

actually caused a signiﬁcant increase in the start

time required. Using the given table and a

graphing calculator, (a) ﬁnd a quadratic regression

equation that models the data. Use this equation to

(b) estimate how long it would take to get a group

of ﬁve tourists ready, (c) estimate the tour capacity

if start-up time can be no longer than 10 min, and

(d) estimate the fastest start time that could be

expected. Round to the nearest hundredth as

necessary.

48. Gardening: The

production of a garden

can be diminished not

only by lack of water, but

also by overwatering.

Shay has kept diligent

records of her 100-ft

tomato garden’s weekly

production, as well as

the amount of water it received through watering

and rain. Use the given table and a graphing

calculator to (a) ﬁnd a quadratic regression

equation that models the data. Then use this

equation to (b) estimate how many tomatoes she

Registration

Day Total

1 791

2 1688

3 2407

4 3067

5 3692

No. of Start-up

Tourists Time (sec)

2 206

4 115

663

979

11 154

13 269

Ticket Sales

Week Total

1 17,751

2 31,266

3 45,311

4 54,986

Water No. of

Total (gal) Tomatoes

77 11

132 25

198 29

256 20

315 1

cob19545_ch03_329-339.qxd 8/10/10 8:26 PM Page 337

can expect when the garden receives 156 gal of

water per week, (c) estimate how much water

the garden received if there were 15 tomatoes

produced per week, and (d) estimate the maximum

number of tomatoes she can expect from the garden

in a week. Round to the nearest ten-thousandth as

necessary.

49. Weight of a

fetus: The

growth rate of a

fetus in the

mother’s womb

(by weight in

grams) is

modeled by the

graph shown

here, beginning

with the 25th

week of

gestation. (a) Calculate the average rate of change

(slope of the secant line) between the 25th week

and the 29th week. Is the slope of the secant line

positive or negative? Discuss what the slope means

in this context. (b) Is the fetus gaining weight faster

between the 25th and 29th week, or between the

32nd and 36th week? Compare the slopes of both

secant lines and discuss.

50. Fertility rates:

Over the years,

fertility rates for

women in the

United States

(average number

of children per

woman) have

varied a great

deal, though in

the twenty-ﬁrst

century they’ve

begun to level out. The graph shown models this

fertility rate for most of the twentieth century.

(a) Calculate the average rate of change from the

years 1920 to 1940. Is the slope of the secant line

positive or negative? Discuss what the slope means

in this context. (b) Calculate the average rate of

change from the year 1940 to 1950. Is the slope of

the secant line positive or negative? Discuss what

the slope means in this context. (c) Was the fertility

rate increasing faster from 1940 to 1950, or from

1980 to 1990? Compare the slope of both secant

lines and comment.

Source: Statistical History of the United States from Colonial Times to Present

For Exercises 51 to 56, use the formula for the average

rate of change .

51. Average rate of change: For , (a) calculate

the average rate of change for the interval

to and (b) calculate the average rate of

change for the interval to . (c) What do

you notice about the answers from parts (a) and

(b)? (d) Sketch the graph of this function along

with the lines representing these average rates of

change and comment on what you notice.

52. Average rate of change: Knowing the general

shape of the graph for , (a) is the

average rate of change greater between and

or between and ? Why?

(b) Calculate the rate of change for these intervals

and verify your response. (c) Approximately how

many times greater is the rate of change?

53. Height of an arrow: If an

arrow is shot vertically from a

bow with an initial speed of

192 ft/sec, the height of the

arrow can be modeled by the

function ,

where h(t) represents the height of the arrow

after t sec (assume the arrow was shot from

ground level).

a. What is the arrow’s height at sec?

b. What is the arrow’s height at sec?

c. What is the average rate of change from

to ?

d. What is the rate of change from to

? Why is it the same as (c) except for

the sign?

54. Height of a water rocket:Although they have

been around for decades, water rockets continue to

be a popular toy. A plastic rocket is ﬁlled with

water and then pressurized using a handheld pump.

The rocket is then released and off it goes! If the

rocket has an initial velocity of 96 ft/sec, the height

of the rocket can be modeled by the function

, where h(t) represents the

height of the rocket after t sec (assume the rocket

was shot from ground level).

a. Find the rocket’s height at and

sec.

b. Find the rocket’s height at sec.

c. Would you expect the average rate of change

to be greater between and or

between and ? Why?

d. Calculate each rate of change and discuss your

answer.

t ⫽ 3t ⫽ 2

t ⫽ 2,t ⫽ 1

t ⫽ 3

t ⫽ 2

t ⫽ 1

h1t2⫽⫺16t

⫹ 96t

t ⫽ 11

t ⫽ 10

t ⫽ 2

t ⫽ 1

t ⫽ 2

t ⫽ 1

h1t2⫽⫺16t

⫹ 192t

x ⫽ 8x ⫽ 7x ⫽ 1

x ⫽ 0

1x2⫽ 1

x ⫽ 2x ⫽ 1

x ⫽⫺1

x ⫽⫺2

1x2⫽ x

f 1x

2ⴚ f 1x

ⴚ x

338 CHAPTER 3 Quadratic Functions and Operations on Functions 3–58

College Algebra G&M—

800

1200

1600

2000

26 28

Weight (g)

30 32 34 36 38 40 42

2400

2800

3200

3400

3600

Age (weeks)

(25, 900)

(29, 1100)

(32, 1600)

(36, 2600)

(40, 3200)

3800

Full term

1.0

2.0

30 40

Rate (children per woman)

50 60 70 80 90 100 110

(10, 3.4)

(20, 3.2)

(40, 2.2)

(60, 3.6)

(50, 3.0)

(70, 2.4)

(80, 1.8)

(90, 2.0)

3.0

4.0

Year (10 → 1910)

cob19545_ch03_329-339.qxd 8/10/10 8:26 PM Page 338

55. Velocity of a falling object: The impact velocity

of an object dropped from a height is modeled by

where v is the velocity in feet per

second (ignoring air resistance), g is the

acceleration due to gravity (32 ft/sec

near the

Earth’s surface), and s is the height from which

the object is dropped.

a. Find the velocity at ft and ft.

b. Find the velocity at ft and ft.

c. Would you expect the average rate of change

to be greater between and or

between and

d. Calculate each rate of change and discuss your

answer.

s ⫽ 20?s ⫽ 15

s ⫽ 10,s ⫽ 5

s ⫽ 20s ⫽ 15

s ⫽ 10s ⫽ 5

v ⫽ 12gs

56. Temperature drop: One day in November, the town

of Coldwater was hit by a sudden winter storm that

caused temperatures to plummet. During the storm,

the temperature T (in degrees Fahrenheit) could be

modeled by the function ,

where h is the number of hours since the storm

began. Graph the function and use this information

to answer the following questions.

a. What was the temperature as the storm began?

b. How many hours until the temperature dropped

below zero degrees?

c. How many hours did the temperature remain

below zero?

d. What was the coldest temperature recorded

during this storm?

T1h2⫽ 0.8h

⫺ 16h ⫹ 60

3–59 Section 3.4 Quadratic Models; More on Rates of Change 339

College Algebra G&M—

䊳

EXTENDING THE CONCEPT

57. The function gives the amount of air

(in cubic inches) that a compressor has pumped out

after t sec. The volume of a spherical balloon being

inﬂated by this compressor is given by ,

with the radius of the balloon modeled by

, where r(t) is the

radius after t sec.

a. If the balloon pops when the radius is at its

maximum, what is the maximum volume of

the balloon?

b. What amount of air (the volume) was needed

to pop the balloon?

c. Calculate the average rates of change and

during the ﬁrst second of inﬂation and the

last second of inﬂation. Compare the results.

¢V

¢r

¢t

r1t2⫽⫺0.02t

⫹ 0.76t ⫹ 2.26

V1r2⫽

␲r

A1t2⫽ 200t

58. In Exercise 44, you were provided with a formula

called the difference quotient. This formula can be

derived by ﬁnding the average rate of change of a

function f(x) over an interval .

a. Use the deﬁnition of average rate of change to

derive the formula for the difference quotient.

b. Find and simplify the difference quotient of

59. The ﬂoor function and the ceiling

function studied in Section 2.5 can

produce some interesting average rates of change.

The average rate of change of these two functions

over any interval 1 unit or longer must lie within

what range of values?

g1x2⫽ <x=

1x2⫽ :x;

1x2⫽ x

⫹ 3x

3x, x ⫹ h4

䊳

MAINTAINING YOUR SKILLS

60. (1.1) Complete the squares in x and y to ﬁnd the

center and radius of the circle deﬁned by

. Then graph the circle on a

graphing calculator.

61. (1.5) Solve the following inequalities graphically

using the Intersection-of-Graphs method. Round to

nearest hundredths when necessary.

b. x ⫺

13 ⫺ x27 710.2x ⫹ 0.52

x ⫺ 5

x ⫺ 2

6 2

⫹ y

⫹ 6x ⫺ 8y ⫽ 0

62. (3.3) Find an equation of the quadratic function

with vertex and y-intercept (0, 7).

63. (2.2/2.5) Given , ﬁnd

the equation of g(x), given its graph is the same as

f(x) but translated right 3 units and reﬂected across

the x-axis.

1x2⫽ •

|x ⫹ 3| x 6 ⫺2

⫺

xxⱖ⫺2

1⫺5, ⫺32

cob19545_ch03_329-339.qxd 8/10/10 8:26 PM Page 339