Coburn J.W., Herdlick J.D. College Algebra: Graphs and Models
Подождите немного. Документ загружается.

EXAMPLE 7
䊳
Computing a Difference Quotient and Average Rates of Change
For ,
a. Compute the difference quotient.
b. Find the average rates of change in the intervals [1.9, 2.0] and [3.6, 3.7].
c. Sketch the graph of f along with the secant lines and comment on what you notice.
Solution
䊳
a. For
Using this result in the difference quotient yields,
eliminate parentheses
combine like terms
factor out
h
result
b. For the interval [1.9, 2.0], and
. The slope of the secant line is
. For the
interval [3.6, 3.7], and .
The slope of this secant line is
.
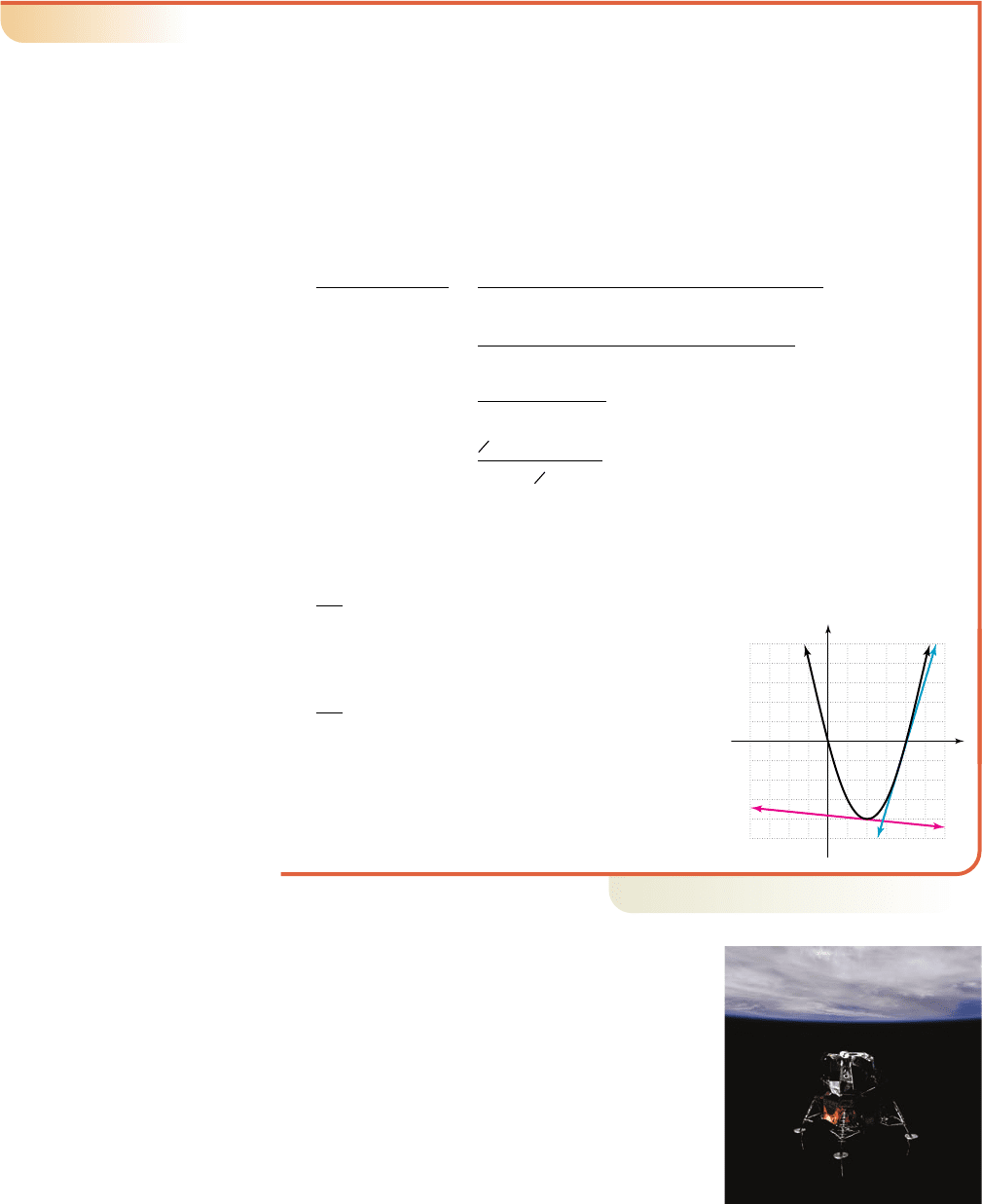
c. After sketching the graph of f and the secant
lines from each interval (see the figure), we
note the slope of the first line (in red) is
negative and very near zero, while the slope of
the second (in blue) is positive and very steep.
Now try Exercises 39 through 50
䊳
It is important that you see these calculations
as much more than just an algebraic exercise. If
the parabola were modeling the distance a rocket
has traveled after the retro-rockets fired, the differ-
ence quotient could provide us with valuable in-
formation regarding the decreasing velocity of the
rocket, and even help pinpoint the moment the
velocity was zero.
¢y
¢x
⫽ 213.62⫺ 4 ⫹ 0.1 ⫽ 3.3
h ⫽ 0.1x ⫽ 3.6
¢y
¢x
⫽ 211.92⫺ 4 ⫹ 0.1 ⫽⫺0.1
h ⫽ 0.1
x ⫽ 1.9
⫽ 2x ⫺ 4 ⫹ h
⫽
h
12x ⫹ h ⫺ 42
h
⫽
2xh ⫹ h
2
⫺ 4h
h
⫽
x
2
⫹ 2xh ⫹ h
2
⫺ 4x ⫺ 4h ⫺ x
2
⫹ 4x
h
f
1x ⫹ h2⫺ f 1x2
h
⫽
1x
2
⫹ 2xh ⫹ h
2
⫺ 4x ⫺ 4h2⫺ 1x
2
⫺ 4x2
h
⫽ x
2
⫹ 2xh ⫹ h
2
⫺ 4x ⫺ 4h
f
1x2⫽ x
2
⫺ 4x, f 1x ⫹ h2⫽ 1x ⫹ h2
2
⫺ 41x ⫹ h2
f
1x2⫽ x
2
⫺ 4x
360 CHAPTER 3 Quadratic Functions and Operations on Functions 3–80
College Algebra G&M—
6⫺4
⫺5
5
x
y
substitute into the
difference quotient
cob19545_ch03_353-370.qxd 8/10/10 7:51 PM Page 360
EXAMPLE 8
䊳
Use the difference quotient to find an average rate of change formula for the
reciprocal function Then use the formula to find the average rate of
change on the intervals [0.5, 0.51] and [3, 3.01]. Note for both intervals.
Solution
䊳
For we have and we compute as follows:
difference quotient
substitute for and for
common denominator
simplify numerator
invert and multiply
This is the formula for computing rates of change given
To find on the interval [0.5, 0.51] we have:
substitute 0.5 for
x
, 0.01 for
h
result (approximate)
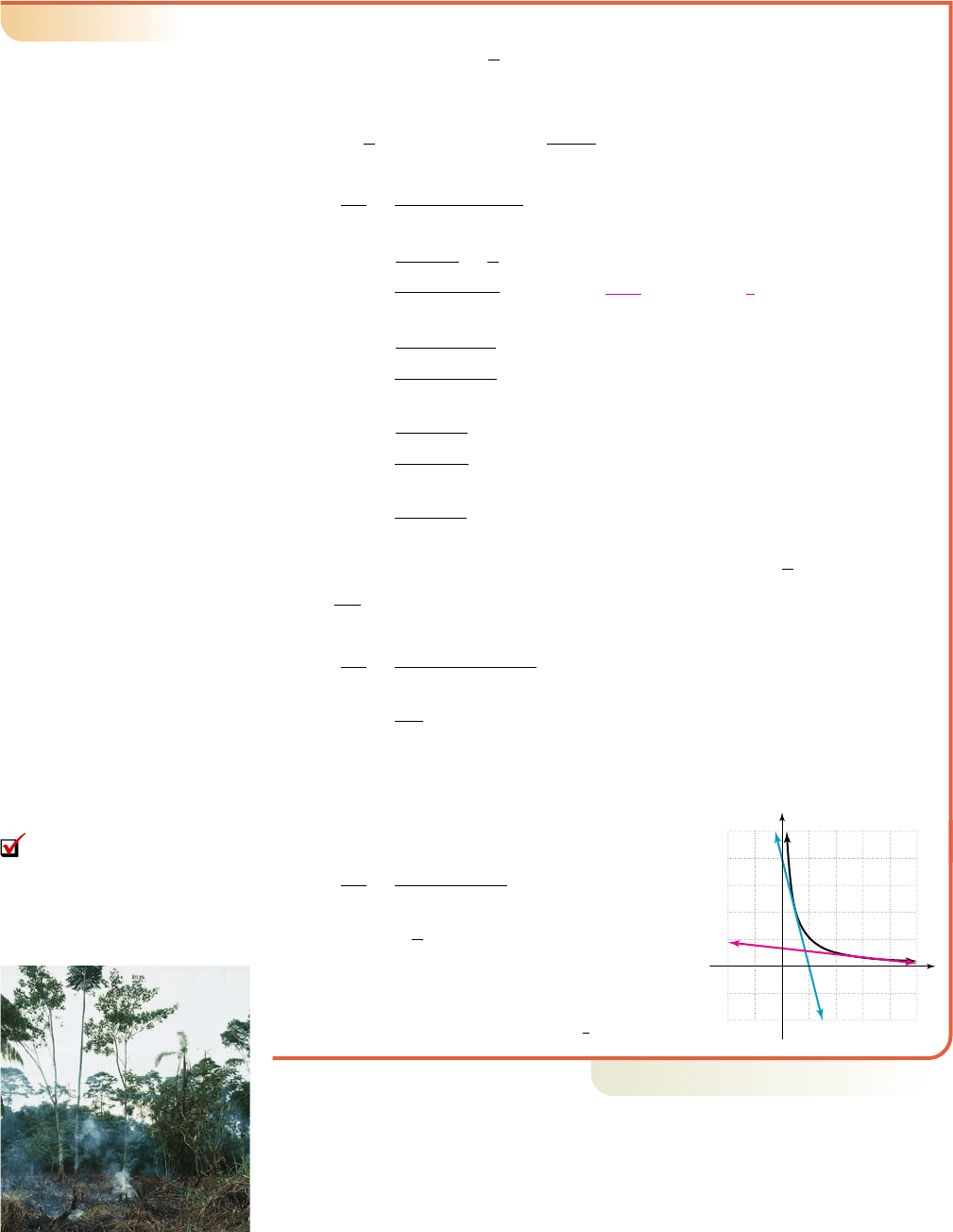
On this interval y is decreasing by about 4 units
for every 1 unit x is increasing. The slope of the
secant line (in blue) through these points is
For the interval [3, 3.01] we have
substitute 3 for
x
, 0.01 for
h
result (approximate)
On this interval, y is decreasing 1 unit for every
9 units x is increasing. The slope of the secant line
(in red) through these points is .
Now try Exercises 51 through 54
䊳
In context, suppose the graph of f were modeling the declining area of the rainforest
over time. The difference quotient would give us information on just how fast the de-
struction was taking place (and give us plenty of cause for alarm).
m ⬇ ⫺
1
9
⬇ ⫺
1
9
¢y
¢x
⫽
⫺1
13 ⫹ 0.012132
m ⬇ ⫺4.
⬇
⫺4
1
¢y
¢x
⫽
⫺1
10.5 ⫹ 0.01210.52
¢y
¢x
f
1x2⫽
1
x
.
⫽
⫺1
1x ⫹ h2x
⫽
⫺h
1x ⫹ h2x
h
⫽
x ⫺ 1x ⫹ h2
1x ⫹ h2x
h
f 1x2
1
x
f 1x ⫹ h2
1
x ⫹ h
⫽
1
1x ⫹ h2
⫺
1
x
h
¢y
¢x
⫽
f
1x ⫹ h2⫺ f 1x2
h
f
1x ⫹ h2⫽
1
x ⫹ h
f 1x2⫽
1
x
h ⫽ 0.01
f
1x2⫽
1
x
.
3–81 Section 3.6 The Composition of Functions and the Difference Quotient 361
College Algebra G&M—
5⫺2
⫺2
5
x
y
C. You’ve just seen how
we can apply the difference
quotient to find average rates
of change for nonlinear
functions
cob19545_ch03_353-370.qxd 8/10/10 7:51 PM Page 361

D. Applications of Composition and the Difference Quotient
Suppose that due to a collision, an oil tanker is spewing oil into the open ocean. The oil
is spreading outward in a shape that is roughly circular, with the radius of the circle mod-
eled by the function where t is the time in minutes and ris measured in feet.
How could we determine the area of the oil slick in terms of t? As you can see, the radius
depends on the time and the area depends on the radius. In diagram form we have:
It is possible to create a direct relationship between the elapsed time and the area
of the circular spill using a composition of functions.
EXAMPLE 9
䊳
Composition and the Area of an Oil Spill
Given and
a. Write A directly as a function of t by computing .
b. Find the area of the oil spill after 30 min.
Solution
䊳
a. The function A squares inputs, then multiplies by .
r
(
t
) is the input for
A
square input, multiply by
substitute 2 for
r
(
t
)
result
Since the result contains no variable r, we can now compute the area of the
spill directly, given the elapsed time t (in minutes):
b. To find the area after 30 min, use
composite function
substitute 30 for
t
simplify
result (rounded to the nearest unit)
After 30 min, the area of the spill is approximately 377 ft
2
.
Now try Exercises 57 through 62
䊳
EXAMPLE 10
䊳
Composition and Related Populations
Using a statistical study, environmentalists find
a current population of 600 wolves in the
county, and believe the wolf population w will
decrease as the human population x grows,
according to the formula .
Further, the population of rodents and small
animals r depends on the number of wolves w,
with the rodent population estimated by
.
a. Evaluate r(w) for to find the current rodent population, then use a
composition to find a function modeling how the human population relates
directly to the number of rodents.
b. Use the function to estimate the number of rodents in the county, if the human
population grows by 35,000.
w ⫽ 600
r1w2⫽ 10,000 ⫺ 9.5w
w1x2⫽ 600 ⫺ 0.02x
⬇ 377
⫽ 120
A1302⫽ 41302
A1t2⫽ 4t
t ⫽ 30.
A1t2⫽ 4t.
⫽ 4t
1t ⫽ 321t4
2
#
⫽ 3r1t24
2
#
1A ⴰ r21t2⫽ A3r1t24
1A ⴰ r21t2
A1r2⫽ r
2
,r1t2⫽ 21t
Elapsed time t Radius depends on time: r(t) Area depends on radius: A(r)
r1t2⫽ 21t,
362 CHAPTER 3 Quadratic Functions and Operations on Functions 3–82
College Algebra G&M—
cob19545_ch03_353-370.qxd 11/25/10 3:48 PM Page 362

Solution
䊳
a. Since , there are currently 4300 rodents in the county. The number
of rodents and small animals is a function of w: , and the
number of wolves w is a function of human population .
To find a function for r in terms of x, we use the composition .
r
depends on
w
compose
r
with
w
(
x
)
distribute
simplify,
r
depends on
x
b. Evaluating r(35,000) gives 10,950 rodents, showing a decline in the wolf
population will eventually cause the rodent population to flourish, with an adverse
effect on humans. In cases like these, a careful balance should be the goal.
Now try Exercises 63 and 64
䊳
You might be familiar with Galileo Galilei and his studies of gravity. According to
popular history, he demonstrated that unequal weights will fall equal distances in equal
time periods, by dropping cannonballs from the upper floors of the Leaning Tower of
Pisa. Neglecting air resistance, the distance an object falls is modeled by the function
, where d(t) represents the distance fallen after t sec. Due to the effects of
gravity, the velocity of the object increases as it falls. In other words, the velocity or the
average rate of change is a nonconstant (increasing) quantity. We can analyze
this rate of change using the difference quotient.
EXAMPLE 11
䊳
Applying the Difference Quotient in Context
A construction worker drops a heavy wrench from atop a
girder of a new skyscraper. Use the function to
a. Compute the distance the wrench has fallen after
2 sec and after 7 sec.
b. Find a formula for the velocity of the wrench (average
rate of change in distance per unit time).
c. Use the formula to find the rate of change in the
intervals [2, 2.01] and [7, 7.01].
d. Graph the function and the secant lines representing
the average rate of change. Comment on what you
notice.
Solution
䊳
a. Substituting and in the given function
yields
evaluate
square input
multiply
After 2 sec, the wrench has fallen 64 ft; after 7 sec, the wrench has fallen 784 ft.
b. For , which we compute separately.
substitute for
t
square binomial
distribute 16 ⫽ 16t
2
⫹ 32th ⫹ 16h
2
⫽ 161t
2
⫹ 2th ⫹ h
2
2
t ⫹ h d1t ⫹ h2⫽ 161t ⫹ h2
2
d1t2⫽ 16t
2
, d1t ⫹ h2⫽ 161t ⫹ h2
2
⫽ 784 ⫽ 64
⫽ 161492 ⫽ 16142
d1t2⫽ 16t
2
d172⫽ 16172
2
d122⫽ 16122
2
t ⫽ 7t ⫽ 2
d1t2⫽ 16t
2
¢distance
¢time
d1t2⫽ 16t
2
r1x2⫽ 4300 ⫹ 0.19x
⫽ 10,000 ⫺ 5700 ⫹ 0.19x
r3w1x24⫽ 10,000 ⫺ 9.53600 ⫺ 0.02x4
r1w2⫽ 10,000 ⫺ 9.5w
1r ⴰ w21x2⫽ r3w1x24
x: w1x2⫽ 600 ⫺ 0.02x
r1w2⫽ 10,000 ⫺ 9.5w
r16002⫽ 4300
3–83 Section 3.6 The Composition of Functions and the Difference Quotient 363
College Algebra G&M—
cob19545_ch03_353-370.qxd 8/12/10 6:02 PM Page 363
Using this result in the difference quotient yields
substitute into the difference quotient
eliminate parentheses
combine like terms
factor out
h
and simplify
result
For any number of seconds t and h a small increment of time thereafter, the
velocity of the wrench is modeled by .
c. For the interval and :
substitute 2 for
t
and 0.01 for
h
Two seconds after being dropped, the velocity of the wrench is close to
64.16 ft/sec (44 mph). For the interval and :
substitute 7 for
t
and 0.01 for
h
Seven seconds after being dropped, the velocity of the wrench is
approximately 224.16 ft/sec (about 153 mph).
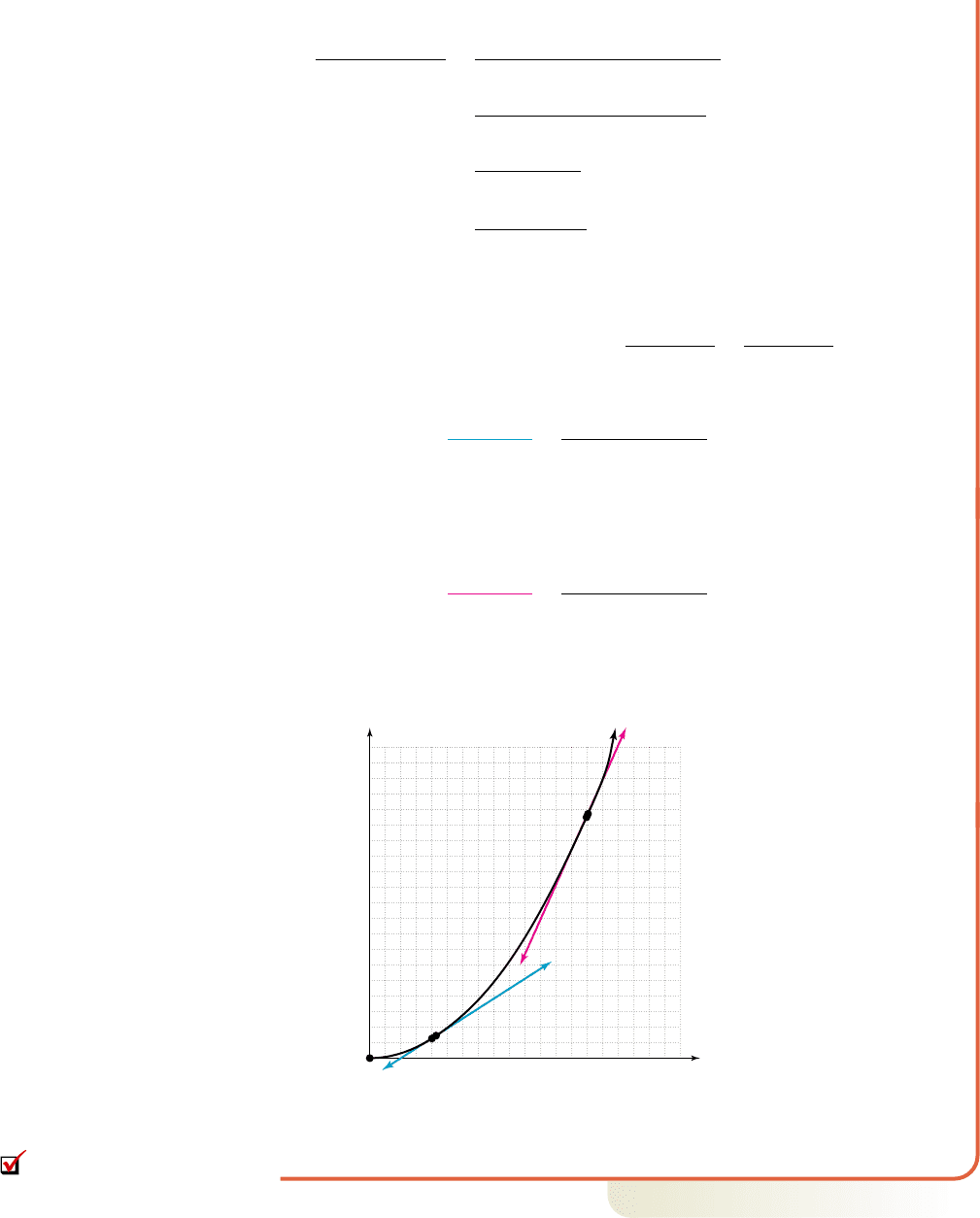
d.
The velocity increases with time, as indicated by the steepness of each
secant line.
Now try Exercises 65 through 68
䊳
x
0
y
200
1
400
600
800
1000
23456789
Time in seconds
Distance fallen (ft)
10
⫽ 224 ⫹ 0.16 ⫽ 224.16
¢distance
¢time
⫽
32172⫹ 1610.012
1
h ⫽ 0.013t, t ⫹ h4⫽ 37, 7.014, t ⫽ 7
⫽ 64 ⫹ 0.16 ⫽ 64.16
¢distance
¢time
⫽
32122⫹ 1610.012
1
h ⫽ 0.013t, t ⫹ h4⫽ 32, 2.014, t ⫽ 2
¢distance
¢time
ⴝ
32t ⴙ 16h
1
⫽ 32t ⫹ 16h
⫽
h132t ⫹ 16h2
h
⫽
32th ⫹ 16h
2
h
⫽
16t
2
⫹ 32th ⫹ 16h
2
⫺ 16t
2
h
d1t ⫹ h2⫺ d1t2
h
⫽
116t
2
⫹ 32th ⫹ 16h
2
2⫺ 16t
2
h
364 CHAPTER 3 Quadratic Functions and Operations on Functions 3–84
College Algebra G&M—
D. You’ve just seen how
we can apply the composition
of functions and the difference
quotient in context
cob19545_ch03_353-370.qxd 8/10/10 7:52 PM Page 364

3.6 EXERCISES
2. The notation indicates that g(x) is the input
value for f(x), which is written .
1f ⴰ g21x2
3. For functions f and g, the domain of is the
set of all x in the of g, such that
is in the domain of f.
1f ⴰ g21x2
4. The average rate of change formula becomes the
quotient by substituting for
x
2
and for x
1
.
5. Discuss/Explain how and why using the the
difference quotient differs from using the average
rate of change formula.
6. Discuss/Explain how the domain of
is determined, given and
.g1x2⫽
2x
x ⫺ 1
f
1x2⫽ 12x ⫹ 7
1f ⴰ g21x2
䊳
CONCEPTS AND VOCABULARY
Fill in each blank with the appropriate word or phrase. Carefully reread the section if needed.
1. When evaluating functions, if the input value is a
function itself, the process is called a of
functions.
3–85 Section 3.6 The Composition of Functions and the Difference Quotient 365
College Algebra G&M—
䊳
DEVELOPING YOUR SKILLS
7. Given find f(7),
f(2a), and .
8. Given find g(3t), and
.
For each pair of functions below, find (a) h(x) ⫽ ( f ⴰ g)(x)
and (b) H(x) ⫽ (g ⴰ f)(x), and (c) determine the domain
of each result.
9. and
10. and
11. and
12. and
13. and
14. and
15. and
16. and
17. and
18. and
For the functions f and g given, h(x) ⫽ ( f ⴰ g)(x). Use a
calculator to evaluate h(⫺3), h( ), , and h(5). If
an error message is received, explain why.
19.
20. , g1x2⫽ x ⫺ 2f
1x2⫽⫺x
2
⫺ 15x
g1x2⫽ x ⫹ 1f
1x2⫽ x
2
⫹ 3x ⫺ 4,
ha
1
2
b22
g1x2⫽ 3x ⫺ 5f 1x2⫽
冟
x ⫺ 2
冟
g1x2⫽⫺3x ⫹ 1f
1x2⫽
冟
x
冟
⫺ 5
g1x2⫽ x ⫺ 2f
1x2⫽ x
2
⫺ 4x ⫹ 2
g1x2⫽ x ⫹ 3f
1x2⫽ x
2
⫹ x ⫺ 4
g1x2⫽ 3x ⫹ 2f
1x2⫽ 2x
2
⫺ 1
g1x2⫽ x ⫹ 2f
1x2⫽ x
2
⫺ 3x
g1x2⫽ 4x ⫺ 1f
1x2⫽ 1x ⫹ 5
g1x2⫽ 3x ⫹ 4f 1x2⫽ 1x ⫺ 3
g1x2⫽ 29 ⫺ xf 1x2⫽ x ⫹ 3
g1x2⫽ 2x ⫺ 5f
1x2⫽ 1x ⫹ 3
g1t ⫹ 12
g1⫺32, g122,g1x2⫽ x
3
⫺ 9x,
f
1a ⫺ 22
f
1⫺22,f 1x2⫽ x
2
⫺ 5x ⫺ 14,
21. ,
22. ,
23. ,
24. ,
For the functions f(x) and g(x) given, analyze the
domain of (a) ( )(x) and (b) ( )(x), then (c) find
the actual compositions and comment.
25. and
26. and
27. and
28. and
29. For and
find h(5) in two ways:
a. b. f[g(5)]
30. For , and
find in two ways:
a. b. p3q1⫺2241p ⴰ q21⫺22
H1⫺22H1x2⫽ 1p ⴰ q21x2,
p1x2⫽ x
2
⫺ 8, q1x2⫽ x ⫹ 2
1f ⴰ g2152
h1x2⫽ 1f ⴰ g21x2,
f
1x2⫽ x
2
⫺ 8, g1x2⫽ x ⫹ 2,
g1x2⫽
1
x ⫺ 2
f 1x2⫽
3
x
g1x2⫽
1
x ⫺ 5
f 1x2⫽
4
x
g1x2⫽
x
x ⫺ 2
f
1x2⫽
⫺3
x
g1x2⫽
5
x
f
1x2⫽
2x
x ⫹ 3
g ⴰ ff ⴰ g
g1x2⫽ x
2
⫺ 11f 1x2⫽
7
x ⫹ 2
g1x2⫽ x
2
⫺ 9f 1x2⫽ 24 ⫺ 3x
g1x2⫽
1
2x ⫺ 1
f
1x2⫽
1
x
2
g1x2⫽
72
x ⫺ 5
f
1x2⫽ 1x ⫹ 82
2
cob19545_ch03_353-370.qxd 11/29/10 10:37 AM Page 365
31. For , find two
functions f and g such that .
32. For , find two functions
p and q such that .
33. Given , and
, find and
.
34. Given and , find
(a) , (b) , (c) , and
(d) .
35. Reading a graph: Use
the given graph to find the
result of the operations
indicated.
Note
, and
so on.
a.
b.
c. d.
e. f.
g. h.
36. Reading a graph: Use
the given graph to find the
result of the operations
indicated.
Note
, and so on.
a.
b.
c. d.
e. f.
g. h.
37. Given , , (a) state
the domain of f and g, then (b) use a graphing
calculator to study the graph of .
Finally, (c) algebraically determine the domain of
h, and reconcile it with the graph.
h1x2⫽ 1f ⴰ g21x2
g1x2⫽
⫺3
x ⫹ 2
f 1x2⫽ 32x ⫹ 1
1p ⴰ p21721q ⴰ q21⫺12
1q ⴰ p21221p ⴰ q21⫺22
1p ⴰ q21021p ⴰ q2142
1p ⴰ q2112
1p ⴰ q21⫺42
q152⫽ 6
p1⫺12⫽⫺2,
1g ⴰ f 21421f ⴰ g2162
1g ⴰ f 21221f ⴰ g21⫺22
1f ⴰ g21021f ⴰ g2142
1f ⴰ g2112
1f ⴰ g21⫺42
g1⫺42⫽⫺1
f
1⫺42⫽ 5,
1g ⴰ f 21x2
1f ⴰ g21x21g ⴰ g21x21f ⴰ f 21x2
g1x2⫽
x ⫺ 3
2
f 1x2⫽ 2x ⫹ 3
q1x2⫽ g3f
13h1x2424
p1x2⫽ f 3g13h1x2424h1x2⫽ x ⫹ 4
f
1x2⫽ 2x ⫺ 1, g1x2⫽ x
2
⫺ 1
1p ⴰ q21x2⫽ H1x2
H1x2⫽ 2
3
x
2
⫺ 5 ⫹ 2
1f ⴰ g21x2⫽ h1x2
h1x2⫽ 11x ⫺ 2
⫹ 12
3
⫺ 5
38. Given , (a) state
the domain of f and g, then (b) use a graphing
calculator to study the graph of .
Finally, (c) algebraically determine the domain of
h, and reconcile it with the graph.
Compute and simplify the difference quotient
for each function given.
39. 40.
41. 42.
43. 44.
45. 46.
Use the difference quotient to find: (a) a rate of change
formula for the functions given and (b)/(c) calculate the
rate of change in the intervals shown. Then (d) sketch
the graph of each function along with the secant lines
and comment on what you notice.
47. 48.
[ ], [0.50, 0.51] [1.9, 2.0], [5.0, 5.01]
49.
[ ], [0.40, 0.41]
50. (Hint: Rationalize the numerator.)
[1, 1.1], [4, 4.1]
Use the difference quotient to find a rate of change
formula for the functions given, then calculate the rate
of change for the intervals indicated. Comment on how
the rate of change in each interval corresponds to the
graph of the function.
51. 52.
53. 54.
31.00, 1.014, 34.00, 4.0143⫺2.01, ⫺2.004, 30.40, 0.414
r1x2⫽ 1xg1x2⫽ x
3
⫹ 1
30.00, 0.014, 33.00, 3.014
30.50, 0.514, 31.50, 1.514
f 1x2⫽ x
2
⫺ 4xj1x2⫽
1
x
2
v1x2⫽ 2x
⫺2.1, ⫺2
g1x2⫽ x
3
⫹ 1
⫺3.0, ⫺2.9
j1x2⫽ x
2
⫺ 6xg1x2⫽ x
2
⫹ 2x
g1x2⫽
⫺3
x
f
1x2⫽
2
x
r1x2⫽ x
2
⫺ 5x ⫹ 2q1x2⫽ x
2
⫹ 2x ⫺ 3
p1x2⫽ x
2
⫺ 2j1x2⫽ x
2
⫹ 3
g1x2⫽ 4x ⫹ 1f
1x2⫽ 2x ⫺ 3
f 1x ⴙ h2ⴚ f 1x2
h
h1x2⫽ 1f ⴰ g21x2
f
1x2⫽ 1x, g1x2⫽
1
x
2
⫺ 2x ⫺ 3
366 CHAPTER 3 Quadratic Functions and Operations on Functions 3–86
College Algebra G&M—
⫺4
6
x
y
f(x)
g(x)
8
⫺4
Exercise 35
8⫺4
⫺4
6
x
y
p(x)
q(x)
4
Exercise 36
䊳
WORKING WITH FORMULAS
55. Transformations via composition: For
and , (a) show that
, then (b) verify the graph
of h is the same as that of f, shifted 2 units to the right.
h1x2⫽ 1 f ⴰ g21x2⫽ x
2
⫺ 1
g1x2⫽ x ⫺ 2f 1x2⫽ x
2
⫹ 4x ⫹ 3
56. Compound annual growth:
The amount of money A in a savings account t yr
after an initial investment of P dollars depends on
the interest rate r. If $1000 is invested for 5 yr, find
f(r) and g(r) such that A1r2⫽ 1f ⴰ g21r2.
A1r2ⴝ P11 ⴙ r2
t
cob19545_ch03_353-370.qxd 8/10/10 7:54 PM Page 366

3–87 Section 3.6 The Composition of Functions and the Difference Quotient 367
College Algebra G&M—
䊳
APPLICATIONS
57. International shoe sizes: Peering inside her
athletic shoes, Morgan notes the following shoe
sizes: US 8.5, UK 6, EUR 40. The function that
relates the U.S. sizes to the European (EUR) sizes
is , where x represents the U.S.
size and g(x) represents the EUR size. The function
that relates European sizes to sizes in the United
Kingdom (UK) is , where x
represents the EUR size and f(x) represents the UK
size. Find the function h(x) that relates the U.S.
measurement directly to the UK measurement by
finding Find the UK size for a
shoe that has a U.S. size of 13.
58. Currency conversion: On a trip to Europe, Megan
had to convert American dollars to euros using the
function where x represents the
number of dollars and E(x) is the equivalent
number of euros. Later, she converts her euros to
Japanese yen using the function
where x represents the number of euros and Y(x)
represents the equivalent number of yen.
(a) Convert 100 U.S. dollars to euros. (b) Convert
the answer from part (a) into Japanese yen.
(c) Express yen as a function of dollars by finding
then use M(x) to convert $100
directly to yen. Do parts (b) and (c) agree?
Source:
2005
World Almanac,
p. 231
59. Currency conversion: While traveling in the Far
East, Timi must convert U.S. dollars to Thai baht
using the function where x
represents the number of dollars and T(x) is the
equivalent number of baht. Later she needs to
convert her baht to Malaysian ringgit using the
function (a) Convert $100 to baht.
(b) Convert the result from part (a) to ringgit.
(c) Express ringgit as a function of dollars using
then use M(x) to convert $100
to ringgit directly. Do parts (b) and (c) agree?
Source:
2005
World Almanac,
p. 231
60. Spread of a fire: Due to a lightning strike, a forest
fire begins to burn and is spreading outward in a
shape that is roughly circular. The radius of the
circle is modeled by the function where t
is the time in minutes and r is measured in meters.
(a) Write a function for the area burned by the fire
directly as a function of t by computing .
(b) Find the area of the circular burn after 60 min.
1A ⴰ r21t2
r1t2⫽ 2t,
M1x2⫽ 1R ⴰ T21x2,
R1x2⫽ 10.9x.
T1x2⫽ 41.6x,
M1x2⫽ 1Y ⴰ E21x2,
Y1x2⫽ 1061x,
E1x2⫽ 1.12x,
h1x2⫽ 1f ⴰ g21x2.
f
1x2⫽ 0.5x ⫺ 14
g1x2⫽ 2x ⫹ 23
61. Radius of a ripple: As Mark drops firecrackers
into a lake one 4th of July, each “pop” caused a
circular ripple that expanded with time. The
radius of the circle is a function of time t.
Suppose the function is where t is in
seconds and r is in feet. (a) Find the radius of the
circle after 2 sec. (b) Find the area of the circle
after 2 sec. (c) Express the area as a function of
time by finding and use A(t) to
find the area of the circle after 2 sec. Do the
answers agree?
A1t2⫽ 1A ⴰ r21t2
r1t2⫽ 3t,
62. Expanding supernova: The surface area of a star
goes through an expansion phase prior to going
supernova. As the star begins expanding, the
radius becomes a function of time. Suppose this
function is , where t is in days and r(t)
is in gigameters (Gm). (a) Find the radius of the
star two days after the expansion phase begins.
(b) Find the surface area after two days. (c)
Express the surface area as a function of time by
finding then use h(t) to compute
the surface area after two days directly. Do the
answers agree?
h1t2⫽ 1S ⴰ r21t2,
r1t2⫽ 1.05t
cob19545_ch03_353-370.qxd 8/12/10 6:05 PM Page 367

63. Composition and dependent relationships: In
the wild, the balance of nature is often very fragile,
with any sudden changes causing dramatic and
unforeseen changes. With a huge increase in
population and tourism near an African wildlife
preserve, the number of lions is decreasing due to
loss of habitat and a disruption in normal daily
movements. This is causing a related increase in
the hyena population, as the lion is one of the
hyena’s only natural predators. If this increase
remains unchecked, animals lower in the food
chain will suffer. If the lion population L depends
on the increase in human population x according
to the formula , and the
hyena population depends on the lion population
as modeled by the formula ,
(a) what is the current lion population
and hyena population? (b) Use a composition to
find a function modeling how the hyena population
relates directly to the number of humans, and use
the function to estimate the number of hyenas in
the area if the human population grows by 16,000.
(c) If the administrators of the preserve consider a
population of 625 hyenas as “extremely detrimental,”
at what point should the human population be
capped?
1x ⫽ 02
H1L2⫽ 650 ⫺ 0.5L
L1x2⫽ 500 ⫺ 0.015x
64. Composition and dependent relationships: The
recent opening of a landfill in the area has caused
the raccoon population to flourish, with an
adverse effect on the number of purple martins.
Wildlife specialists believe the population of
martins p will decrease as the raccoon population
r grows. Further, since mosquitoes are the primary
diet of purple martins, the mosquito population
m is likewise affected. If the first relationship is
modeled by the function and
the second by , (a) what is
the current number of purple martins and
mosquitoes? (b) Use a composition to find a
function modeling how the raccoon population
relates directly to the number of mosquitoes,
and use the function to estimate the number of
mosquitoes in the area if the raccoon population
1r ⫽ 02
m1p2⫽ 50,000 ⫺ 45p
p1r2⫽ 750 ⫺ 3.75r
grows by 50. (c) If the health department considers
36,500 mosquitoes to be a “dangerous level,”
what increase in the raccoon population will
bring this about?
65. Distance to the horizon: The distance that a
person can see depends on how high they’re
standing above level ground. On a clear day,
the distance is approximated by the function
, where d(h) represents the viewing
distance (in miles) at height h (in feet). Use
the difference quotient to find the average rate
of change in the intervals (a) [9, 9.01] and
(b) [225, 225.01]. Then (c) graph the function
along with the lines representing the average
rates of change and comment on what you
notice.
66. Projector lenses: A special magnifying lens is
crafted and installed in an overhead projector.
When the projector is x ft from the screen, the
size P(x) of the projected image is x
2
. Use the
difference quotient to find the average rate of
change for in the intervals (a) [1, 1.01]
and (b) [4, 4.01]. Then (c) graph the function
along with the lines representing the average
rates of change and comment on what you
notice.
67. Fortune and fame: Over the years there have
been a large number of what we know as “one
hit wonders,” persons or groups that published a
memorable or timeless song, but who were
unable to repeat the feat. In some cases, their
fame might be modeled by a quadratic function
as their popularity rose to a maximum, then
faded with time. Suppose the song She’s on Her
Way by Helyn Wheels rode to the top of the
charts in January of 1988, with demand for the
song modeled by . Here, d(t)
represents the demand in 1000s for month
. (a) How many times faster was
the demand growing in March (shortly after
the release) than in June? Use the difference
quotient and the intervals [3, 3.01] for March
t
1t ⫽ 1 S Jan2
d1t2⫽⫺2t
2
⫹ 27t
P1x2⫽ x
2
d1h2⫽ 1.21h
368 CHAPTER 3 Quadratic Functions and Operations on Functions 3–88
College Algebra G&M—
cob19545_ch03_353-370.qxd 8/12/10 6:22 PM Page 368

3–89 Section 3.6 The Composition of Functions and the Difference Quotient 369
College Algebra G&M—
䊳
EXTENDING THE CONCEPT
69. Given and graph
each function on the same axes by plotting the
points that correspond to integer inputs for
Do you notice anything? Next, find
and What
happened? Look closely at the functions f and g to
see how they are related. Can you come up with two
additional functions where the same thing occurs?
70. Given , and
, (a) find the new function rule for
h and (b) determine the implied domain of h. Does
this implied domain include , and
as valid inputs? (c) Determine the actual
domain for and discuss the result.
h1x2⫽ 1
f ⴰ g21x2
x ⫽⫺3
x ⫽ 2, x ⫽⫺2
h1x2⫽ 1
f ⴰ g21x2
f
1x2⫽
1
x
2
⫺ 4
, g1x2⫽ 1x ⫹ 1
H1x2⫽ 1g ⴰ f21x2.h1x2⫽ 1f ⴰ g21x2
x 僆 3⫺3, 34.
g1x2⫽ 2
3
x ⫺ 2,f 1x2⫽ x
3
⫹ 2
and [6, 6.01] for June. (b) Determine the month
that demand reached its peak using a graphing
calculator. (c) Was the demand increasing or
decreasing in the month of August? At what
rate?
68. Velocity and fuel economy: It has long been
known that cars and trucks are more fuel efficient
at certain speeds, which is why President Richard
Nixon lowered the speed limit on all federal
highways to 55 mph during the oil embargo of
1974. For heavier and less fuel-efficient vehicles,
the miles per gallon for certain speeds can be
modeled by the function ,
where m(s) represents the mileage (in miles per
gallon) at speed s . (a) Use the
difference quotient to find how many times
10 6 s ⱕ 802
m1s2⫽⫺0.01s
2
⫹ s
faster fuel efficiency is growing near mph
than near mph. Use the intervals [30, 30.1]
and [45, 45.1]. (b) Use a graphing calculator
to determine the speed(s) that maximizes fuel
efficiency for this vehicle. How many miles
per gallon are achieved? (c) Is fuel efficiency
increasing or decreasing at 70 mph? At what
rate?
s ⫽ 45
s ⫽ 30
71. Consider the functions and .
Both graphs appear similar in Quadrant I and both
may “fit” a scatterplot fairly well, but there is a big
difference between them—they decrease as x gets
larger, but they decrease at very different rates.
(a) Assume and use the ideas from this
section to compute the rates of change for f and g
for the interval from to . Were you
surprised? (b) In the interval to ,
will the rate of decrease for each function be
greater or less than in the interval to
? Why?x ⫽ 0.51
x ⫽ 0.5
x ⫽ 0.81x ⫽ 0.8
x ⫽ 0.51x ⫽ 0.5
k ⫽ 1
g1x2⫽
k
x
2
f 1x2⫽
k
x
䊳
MAINTAINING YOUR SKILLS
72. (3.1) Find the sum and product of the complex
numbers and
73. (2.2) Draw a sketch of the functions from memory.
(a) (b) , and
(c) h1x2⫽
冟
x
冟
g1x2⫽ 2
3
xf 1x2⫽ 1x,
2 ⫺ 3i.2 ⫹ 3i
74. (3.2) Use the quadratic formula to solve
75. (1.4) Find an equation of the line perpendicular to
, that also goes through the origin.⫺2x ⫹ 3y ⫽ 9
2x
2
⫺ 3x ⫹ 4 ⫽ 0.
cob19545_ch03_353-370.qxd 8/12/10 6:25 PM Page 369
