Coburn J.W., Herdlick J.D. College Algebra: Graphs and Models
Подождите немного. Документ загружается.

⫺3
3
0
5
EXAMPLE 1
䊳
Solving a Logarithmic Equation
Solve for x and check your answer: .
䊲
Algebraic Solution
original equation
product property
exponential form,
distribute
x
set equal to 0
factor
result x ⫽⫺5 or x ⫽ 2
1x ⫹ 521x ⫺ 22⫽ 0
x
2
⫹ 3x ⫺ 10 ⫽ 0
x
2
⫹ 3x ⫽ 10
1
log 3x 1x ⫹ 324⫽ 1
log x ⫹ log
1x ⫹ 32⫽ 1
log x ⫹ log
1x ⫹ 32⫽ 1
䊲
Graphical Solution
Using the intersection-of-
graphs method, we enter
and . From the domain
we know , indicating
the solution will occur in QI.
After graphing both functions
using the window shown, the
intersection method shows
the only solution is .x ⫽ 2
x 7 0
Y
2
⫽ 1
Y
1
⫽ log X ⫹ log1X ⫹ 32
Check: The “solution” is outside the domain and is ignored. For ,
original equation
substitute 2 for
x
simplify
product property
Property I
You could also use a calculator to verify directly.
Now try Exercises 7 through 14
䊳
log 5 ⫽ 1log 2 ⫹
log 10 ⫽ 1
log12
#
52⫽ 1
log 2 ⫹ log 5 ⫽ 1
log 2 ⫹ log12 ⫹ 32⫽ 1
log x ⫹ log1x ⫹ 32⫽ 1
x ⫽ 2x ⫽⫺5
r
ou
g
g
EXAMPLE 1A
䊳
Solving an Equation Graphically
Solve the equation using
a graphing calculator.
Solution
䊳
Begin by entering the left-hand expression as Y
1
and the right-hand expression as Y
2
(Figure 1.74).
To find points of intersection, press
(CALC) and select option 5:intersect, which
automatically places you on the graphing
window, and asks you to identify the
“First curve?.” As discussed, pressing
three times in succession will identify each
graph, bypass the “Guess?” option, then
find and display the point of intersection
(Figure 1.75). Here the point of intersection
is ( ), showing the solution to this
equation is (for which both
expressions equal 3). This can be verified
by direct substitution or by using the
TABLE feature.
x 2
2, 3
ENTER
TRACE
2nd
21x 32 7
1
2
x 2
Figure 1.74
Figure 1.75
10
10
10
10
Visually, Symbolically, Numerically, and Verbally
▶
Graphical Examples show students how
the calculator can be used to supplement
their understanding of a problem.
viii
Making Connections . . .
“It is widely known that for students to grow stronger algebraically, the concrete and numeric
experiences from their past must give way to more symbolic representations. In this transition
from numeric, to symbolic, to algebraic thinking, the importance of visual connections and verbal
connections is too often overlooked. To reach a deep understanding of rich concepts or subtle ideas,
students must develop the ability to mentally “see” and discuss the concept or idea using the terms
and names needed to describe it accurately. Only then can they begin seeing the connections that
exist between each new concept, and concepts that are already known. A large part of this involves
helping our students to begin thinking visually, to a point where they’re able to see functions like
f(x) = x
2
– 4x as only one of a large family of functions, with graphical attributes that immediately
lead to a discussion of maximums and minimums, end-behavior, zeroes, solutions to inequalities, the
nature of the roots, and the application of these attributes in context. And while it’s important for
students to see that zeroes are x-intercepts and x-intercepts are zeroes, and that the intersection of
two graphs provides a simultaneous solution to the equations forming these graphs, these should not
remain the sole focus of the tool. Graphing calculators allow explorations, investigations, connections,
and visualizations far beyond what’s possible with paper and pencil, and we should use the technology
to aid the development of these mental-visual skills, in addition to solving more true-to-life equations,
engaging more applications, and exploring the more substantial questions involving real data, domain
and range, anticipated graphical behavior, additional uses of lists and tables, and other questions of
interest. We believe this text offers instructors the tools they need to be successful in these endeavors.”
—The Authors
“
I have certainly found the Coburn/Herdlick’s
Precalculus: Graphs and Models textbook
the best approach ever to the teaching of
Precalculus with the inclusion of graphing
calculator.
”
—Alvio Dominguez, Miami-Dade
College-Wolfson
5
“
I think there is a good balance between technology
and paper/pencil techniques. I particularly like how
the technology portion does not take the place of
paper/pencil, but instead supplements it. I think a
lot of departments will like that.
”
—Daniel Brock, Arkansas State University-Beebe
cob19545_fm_i-xxxviii.indd Page viii 22/12/10 4:22 PM user-f467cob19545_fm_i-xxxviii.indd Page viii 22/12/10 4:22 PM user-f467 /Volume/204/MHDQ268/wea25324_disk1of1/0073525324/wea25324_pagefiles/Volume/204/MHDQ268/wea25324_disk1of1/0073525324/wea25324_pagefiles

To help illustrate the Intermediate Value Theorem, many graphing calculators
offer a useful feature called split screen viewing, that enables us to view a table of
values and the graph of a function at the same time. To illustrate, enter the function
(from Example 6) as Y
1
on the screen, then set the viewing
window as shown in Figure 4.4. Set your table in AUTO mode with , then
press the key (see Figure 4.4A) and notice the second-to-last entry on this screen
reads: Full for full screen viewing, Horiz for splitting the screen horizontally with the
graph above a reduced home screen, and G-T, which represents Graph-Table and
splits the screen vertically. In the G-T mode, the graph appears on the left and the
table of values on the right. Navigate the cursor to the G-T mode and press . Press-
ing the key at this point should give you a screen similar to Figure 4.5. Scrolling
downward shows the function also changes sign between and . For more
on this idea, see Exercises 31 and 32.
As a final note, while the intermediate value theorem is a powerful yet simple
tool, it must be used with care. For example, given ,
and seeming to indicate that no zeroes exist in the interval (1, 1). Actually,
there are two zeroes, as seen in Figure 4.6.
p1 127 0,
p1127 0p1 x2x
4
10x
2
5
x 3x 2
GRAPH
ENTER
MODE
¢Tbl 1
Y=
y x
3
9x 6
Figure 4.5
Figure 4.4A
10
25
5
5
Figure 4.6
B. You’ve just seen how
we can use the intermediate
value theorem to identify
intervals containing a
polynomial zero
Most graphing calculators are programmed to work
with imaginary and complex numbers, though for
some models the calculator must be placed in com-
plex number mode. After pressing the key
(located to the right of the option key), the
screen shown in Figure 3.2 appears and we use
the arrow keys to access “ ” and active this
mode (by pressing ). Once active, we can validate
our previous statements about imaginary numbers
(Figure 3.3), as well as verify our previous calculations like those in Examples 3(a), 3(d),
and 4(a) (Figure 3.4). Note the imaginary unit i is the option for the decimal point.
2nd
ENTER
a bi
2nd
MODE
Figure 3.3 Figure 3.4
Figure 3.2
Use Newton’s law of cooling to complete Exercises 75
and 76: T(x) ⫽ T
R
⫹ (T
0
⫺ T
R
)e
kx
.
75. Cold party drinks: Janae was late getting ready for
the party, and the liters of soft drinks she bought
were still at room temperature ( ) with guests
due to arrive in 15 min. If she puts these in her
freezer at , will the drinks be cold enough
( ) for her guests? Assume .
76. Warm party drinks: Newton’s law of cooling
applies equally well if the “cooling is negative,”
meaning the object is taken from a colder medium
and placed in a warmer one. If a can of soft drink is
taken from a cooler and placed in a room
where the temperature is , how long will it take
the drink to warm to ? Assume .
Photochromatic sunglasses: Sunglasses that darken in
sunlight (photochromatic sunglasses) contain millions of
molecules of a substance known as silver halide. The
molecules are transparent indoors in the absence of
ultraviolent (UV) light. Outdoors, UV light from the sun
causes the molecules to change shape, darkening the
lenses in response to the intensity of the UV light. For
certain lenses, the function models the
transparency of the lenses (as a percentage) based on a
UV index x. Find the transparency (to the nearest
percent), if the lenses are exposed to
77. sunlight with a UV index of 7 (a high exposure).
78. sunlight with a UV index of 5.5 (a moderate
exposure)
T1 x2 0.85
x
k ⬇ 0.03165°F
75°F
35°F
k ⬇ 0.03135°F
10°F
73°F
80. Use a trial-and-error process and a graphing
calculator to determine the UV index when the
lenses are 50% transparent.
Modeling inflation: Assuming the rate of inflation is 5%
per year, the predicted price of an item can be modeled
by the function where P
0
represents the
initial price of the item and t is in years. Use this
information to solve Exercises 81 and 82.
81. What will the price of a new car be in the year
2015, if it cost $20,000 in the year 2010?
82. What will the price of a gallon of milk be in the
year 2015, if it cost $3.95 in the year 2010? Round
to the nearest cent.
Modeling radioactive decay: The half-life of a
radioactive substance is the time required for half an
initial amount of the substance to disappear through
decay. The amount of the substance remaining is given
by the formula where h is the half-life,
t represents the elapsed time, and Q(t) represents the
amount that remains (t and h must have the same unit
of time). Use this information to solve Exercises 83
and 84.
83. Some isotopes of the substance known as thorium
have a half-life of only 8 min. (a) If 64 grams are
initially present, how many grams (g) of the
substance remain after 24 min? (b) How many
minutes until only 1 gram (g) of the substance
remains?
Q1 t2 Q
0
1
1
2
2
t
h
,
P1 t2 P
0
11.052
t
,
▶
Calculator Explanations incorporate the
calculator without sacrificing.
▶
Technology Applications show
students how technology can be
used to help apply lessons from
the classroom to real life.
werful
yet
simple
,
l
(
1, 1). Actua
l
p
1
1
2
7
2
5
5
l
ll
ly
y
y,
7
7
7
0
0
0
0
“
The authors give very good uses of the calculator
in every section. I have been using TI calculators
for 15 years and I learned a few new tricks while
reading this book.
”
—George Hurlburt, Corning Community College
ix
our prev
io
(Fig
ure
3.3
and 4(a) (F
g
g
ure
an
an
and
d
“
The technology (graphing calculator) explanations
and illustrations are superb. The level of detail is
valuable; even an experienced user (myself)
learned some new techniques and “tricks” in
reading through the text. The text frequently
references use of the calculator—yet without
sacrificing rigor or mathematical integrity.
”
—Light Bryant, Arizona Western College
w
h
ere t
h
e
the
drin
k
Photochr
omat
sunlight (ph
oto
le
cule
s of
a
molecules ar
e t
ultraviolent
(U
causes the m
ol
l
enses
i
n re
spo
certa
i
n
l
enses
,
transparenc
y
of
U
V i
ndex
x
. Fi
perc
ent),
if
t
h
e
77
li ht
unl
sunl
tght
igh
igh
(p
mole
ole
le
m
le
c
c
cu
m
momo
m
“
I think that the graphing examples, explanations,
and problems are perfect for the average college
algebra student who has never touched a graphing
calculator. . . . . I think this book would be great to
actually have in front of the students.
”
—Dale Duke, Oklahoma City Community College
cob19545_fm_i-xxxviii.indd Page ix 22/12/10 4:23 PM user-f467cob19545_fm_i-xxxviii.indd Page ix 22/12/10 4:23 PM user-f467 /Volume/204/MHDQ268/wea25324_disk1of1/0073525324/wea25324_pagefiles/Volume/204/MHDQ268/wea25324_disk1of1/0073525324/wea25324_pagefiles
x
You want a way to identify the strengths and weaknesses of your class at
the beginning of the term rather than after the fi rst exam.
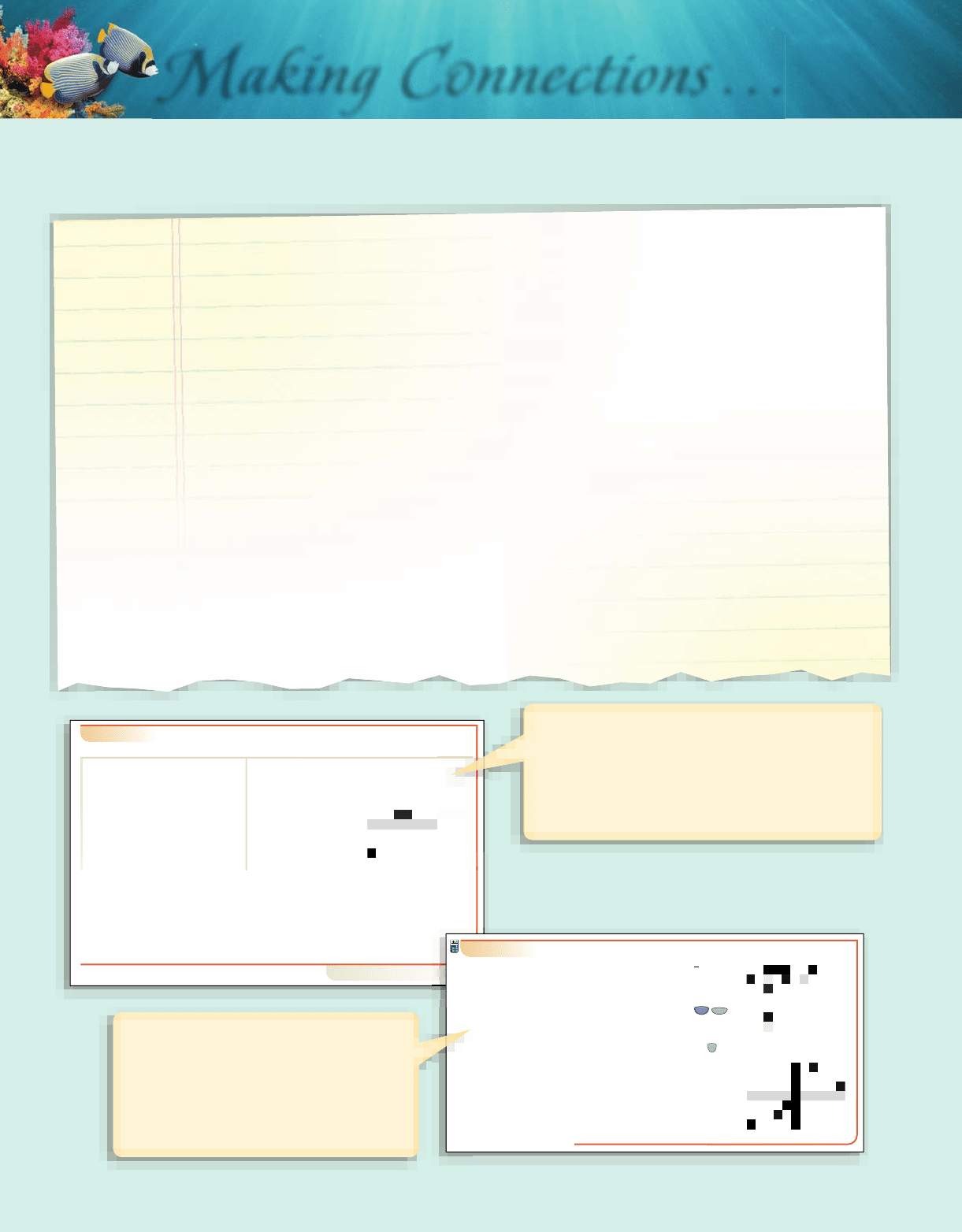
Connect Math Hosted by ALEKS Corporation is an exciting, new assignment and
assessment platform combining the strengths of McGraw-Hill Higher Education and ALEKS Corporation.
Connect Math Hosted by ALEKS is the fi rst platform on the market to combine an artifi cially-intelligent,
diagnostic assessment with an intuitive ehomework platform designed to meet your needs.
Connect Math Hosted by ALEKS Corporation is the culmination of a one-of-a-kind market development
process involving math full-time and adjunct Math faculty at every step of the process. This process
enables us to provide you with a solution that best meets your needs.
Connect Math Hosted by ALEKS Corporation is built by Math educators for Math educators!
Modern Student Homepage
▶ This homepage provides a dashboard for
students to immediately view their assignments,
grades, and announcements for their course.
(Assignments include HW, quizzes, and tests.)
▶ Students can access their assignments through
the course Calendar to stay up-to-date and
organized for their class.
Your students want a well-organized homepage where key
information is easily viewable.
Integrated ALEKS
®
Assessment
▶ This artifi cially-intelligent (AI), diagnostic
assessment identifi es precisely what a student
knows and is ready to learn next.
▶ Detailed assessment reports provide instructors
with specifi c information about where students
are struggling most.
▶ This AI-driven assessment is
the only one of its kind
in an online homework
platform.
1
2
Modern, intuitive,
and simple interface.
about
where
students
t
is
Recommended to be used
as the fi rst assignment in
any course.
ALEKS is a registered trademark of ALEKS Corporation.
cob19545_fm_i-xxxviii.indd Page x 22/12/10 4:23 PM user-f467cob19545_fm_i-xxxviii.indd Page x 22/12/10 4:23 PM user-f467 /Volume/204/MHDQ268/wea25324_disk1of1/0073525324/wea25324_pagefiles/Volume/204/MHDQ268/wea25324_disk1of1/0073525324/wea25324_pagefiles

xi
Effi cient Assignment Navigation
▶ Students have access to immediate
feedback and help while working
through assignments.
▶ Students have direct access
to a media-rich eBook for easy
referencing.
▶ Students can view detailed,
step-by-step solutions
written by instructors
who teach the course,
providing a unique solution
to each and every exercise.
Your students want an assignment page that is easy to use and includes
lots of extra help resources.
Assignment Creation Process
▶ Instructors can select textbook-
specifi c questions organized by
chapter, section, and objective.
▶ Drag-and-drop functionality makes
creating an assignment quick and
easy.
▶ Instructors can preview their
assignments for effi cient editing.
o
n
e
e
ss
r
easy
e
d
,
Students can easily monitor
and track their progress on a
given assignment.
You want a more intuitive and effi cient assignment creation process
because of your busy schedule.
Y
l
3
Y
b
4
TM
www.connectmath.com
Built by Math Educators
for Math Educators
cob19545_fm_i-xxxviii.indd Page xi 22/12/10 4:23 PM user-f467cob19545_fm_i-xxxviii.indd Page xi 22/12/10 4:23 PM user-f467 /Volume/204/MHDQ268/wea25324_disk1of1/0073525324/wea25324_pagefiles/Volume/204/MHDQ268/wea25324_disk1of1/0073525324/wea25324_pagefiles
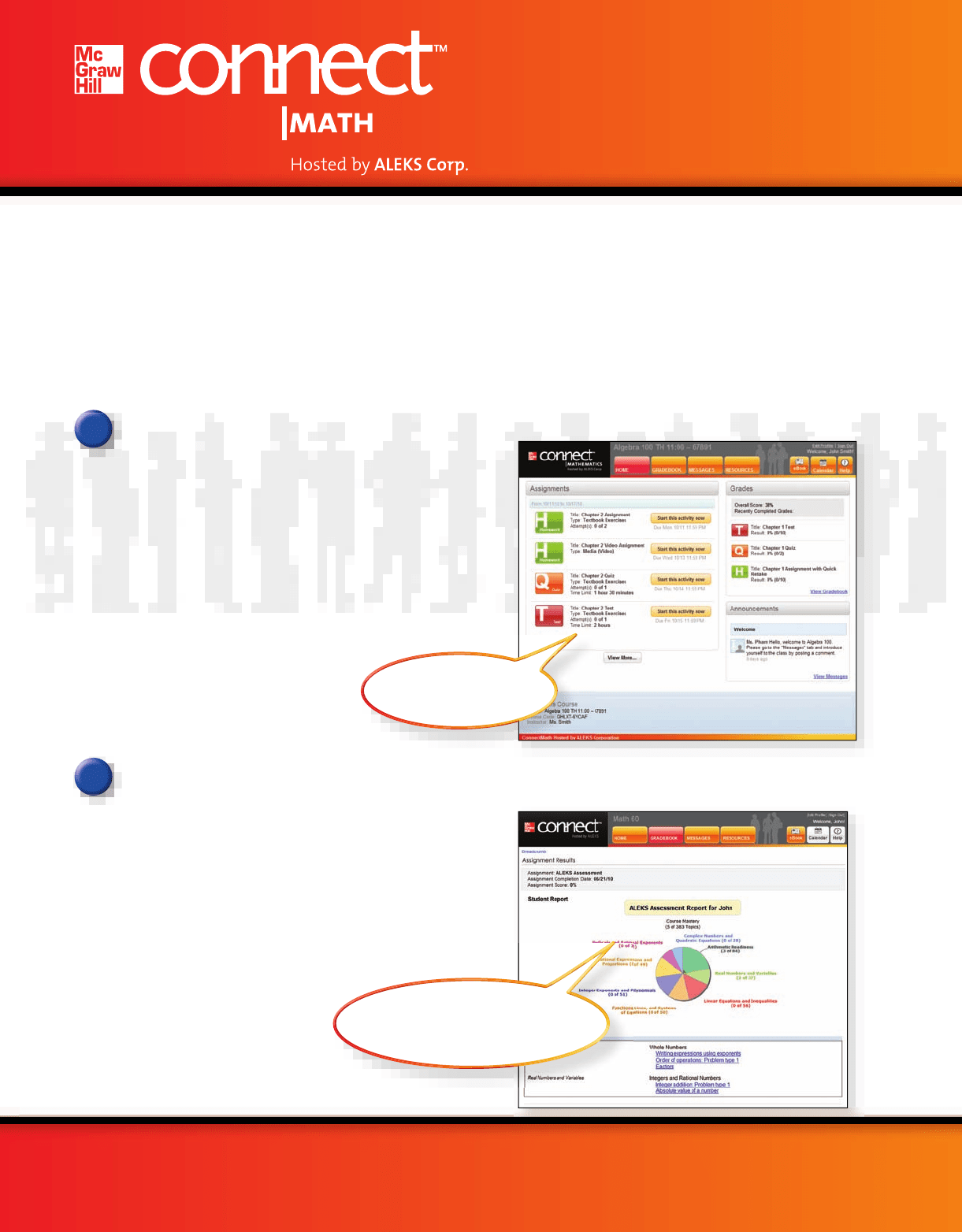
Your students want an interactive eBook with rich functionality
integrated into the product.
You want a fl exible gradebook that is easy to use.
Instructors have the ability
to drop grades as well as
assign extra credit.
Integrated Media-Rich eBook
▶ A Web-optimized eBook is seamlessly
integrated within ConnectPlus Math Hosted
by ALEKS Corp for ease of use.
▶ Students can access videos, images, and
other media in context within each chapter
or subject area to enhance their learning
experience.
▶ Students can highlight, take notes, or even
access shared instructor highlights/notes to
learn the course material.
▶ The integrated eBook provides students
with a cost-saving alternative to traditional
textbooks.
Flexible Instructor Gradebook
▶ Based on instructor feedback,
Connect Math Hosted by ALEKS
Corp’s straightforward design creates
an intuitive, visually pleasing grade
management environment.
▶ Assignment types are color-coded for
easy viewing.
▶ The gradebook allows instructors
the fl exibility to import and export
additional grades.
5
6
xii
cob19545_fm_i-xxxviii.indd Page xii 22/12/10 4:24 PM user-f467cob19545_fm_i-xxxviii.indd Page xii 22/12/10 4:24 PM user-f467 /Volume/204/MHDQ268/wea25324_disk1of1/0073525324/wea25324_pagefiles/Volume/204/MHDQ268/wea25324_disk1of1/0073525324/wea25324_pagefiles

Built by Math Educators
for Math Educators
www.connectmath.com
You want algorithmic content that was developed by math faculty to
ensure the content is pedagogically sound and accurate.
Y
e
7
Digital Content Development Story
The development of McGraw-Hill’s Connect Math Hosted by ALEKS Corp. content involved
collaboration between McGraw-Hill, experienced instructors, and ALEKS, a company known for its
high-quality digital content. The result of this process, outlined below, is accurate content created
with your students in mind. It is available in a simple-to-use interface with all the functionality tools
needed to manage your course.
1. McGraw-Hill selected experienced instructors to work as Digital Contributors.
2. The Digital Contributors selected the textbook exercises to be included in the algorithmic
content to ensure appropriate coverage of the textbook content.
3. The Digital Contributors created detailed, stepped-out solutions for use in the Guided
Solution and Show Me features.
4. The Digital Contributors provided detailed instructions for authoring the algorithm specifi c to
each exercise to maintain the original intent and integrity of each unique exercise.
5. Each algorithm was reviewed by the Contributor, went through a detailed quality control
process by ALEKS Corporation, and was copyedited prior to being posted live.
Connect Math Hosted by ALEKS Corp.
Built by Math Educators for Math Educators
Digital Contributors
Al Bluman, Community College of
Allegheny County
John Coburn, St. Louis Community
College, Florissant Valley
Vanessa Coffelt, Blinn College
Donna Gerken, Miami-Dade College
Kimberly Graham
J.D. Herdlick, St. Louis Community
College, Meramec
Vickie Flanders, Baton Rouge
Community College
Nic LaHue, Metropolitan Community
College, Penn Valley
Nicole Lloyd, Lansing Community College
Jackie Miller, The Ohio State University
Anne Marie Mosher, St. Louis
Community College, Florissant Valley
Reva Narasimhan, Kean University
David Ray, University of Tennessee,
Martin
Kristin Stoley, Blinn College
Stephen Toner, Victor Valley College
Paul Vroman, St. Louis Community
College, Florissant Valley
Michelle Whitmer, Lansing Community
College
Lead Digital
Contributors
Tim Chappell
Metropolitan Community
College, Penn Valley
Jeremy Coffelt
Blinn College
Nancy Ikeda
Fullerton College
Amy Naughten
TM
xiii
cob19545_fm_i-xxxviii.indd Page xiii 22/12/10 4:24 PM user-f467cob19545_fm_i-xxxviii.indd Page xiii 22/12/10 4:24 PM user-f467 /Volume/204/MHDQ268/wea25324_disk1of1/0073525324/wea25324_pagefiles/Volume/204/MHDQ268/wea25324_disk1of1/0073525324/wea25324_pagefiles
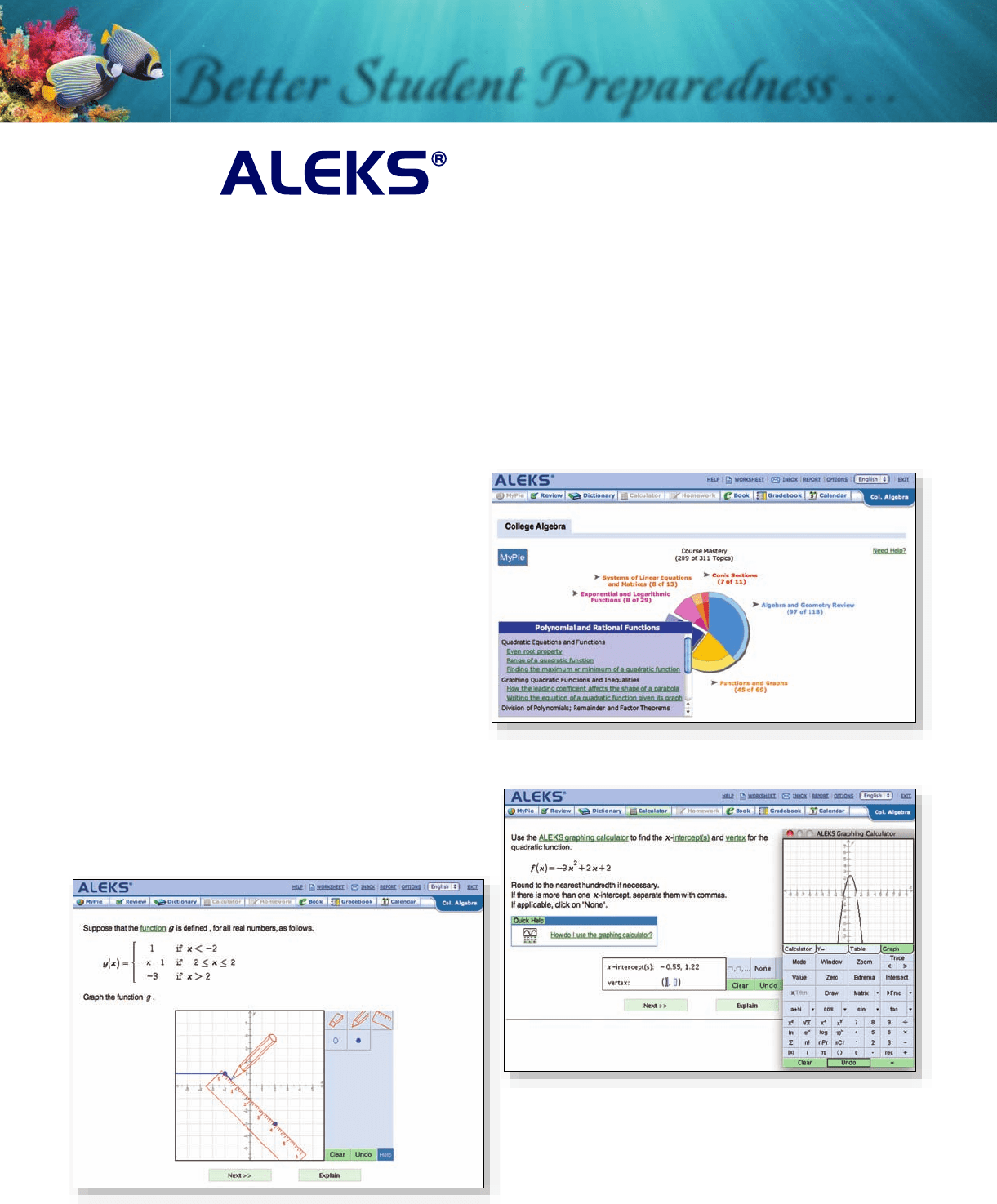
ALEKS College Algebra features hundreds of new course topics to provide comprehensive course coverage, and ALEKS
AI-2, the next generation intelligence engine to dramatically improve student learning outcomes. This enhanced ALEKS
course product allows for better curriculum coverage and seamless textbook integration to help students succeed in
mathematics, while allowing instructors to customize course content to align with their course syllabi.
ALEKS is a Web-based program that uses artificial intelligence and adaptive questioning to assess precisely a student’s
knowledge in College Algebra and provide personalized instruction on the exact topics the student is most ready to learn.
By providing individualized assessment and learning, ALEKS helps students to master course content quickly and easily.
xiv
Better Student Preparedness . . .
Enhanced Course Coverage Enables Seamless
Integration with Textbooks and Syllabi
College Algebra
ALEKS is a registered trademark of ALEKS Corporation.
Topics Added For Comprehensive Coverage:
ALEKS College Algebra includes hundreds of new topics
for comprehensive coverage of course material. To view
College Algebra course content in more detail, please visit:
www.aleks.com/highered/math/course_products
Robust Graphing Features:
ALEKS College Algebra provides more graphing coverage and includes a built-in graphing calculator, an adaptive,
open-response environment, and realistic answer input tools to ensure student mastery.
The ALEKS Pie summarizes a student’s ▶
current knowledge of course material and
provides an individualized learning path with
topics each student is most ready to learn.
The ALEKS Graphing Calculator is ▶
accessible via the Student Module and
can be turned on or off by the instructor.
◀ Realistic Input Tools provide an adaptive,
open-response environment that avoids
multiple-choice questions and ensures
student mastery.
cob19545_fm_i-xxxviii.indd Page xiv 22/12/10 4:24 PM user-f467cob19545_fm_i-xxxviii.indd Page xiv 22/12/10 4:24 PM user-f467 /Volume/204/MHDQ268/wea25324_disk1of1/0073525324/wea25324_pagefiles/Volume/204/MHDQ268/wea25324_disk1of1/0073525324/wea25324_pagefiles
xv
. . .Through Superior Course Management
New Instructor Module Features
for College Algebra
ALEKS is a registered trademark of ALEKS Corporation.
Help Students Achieve Success While
Saving Instructor Time
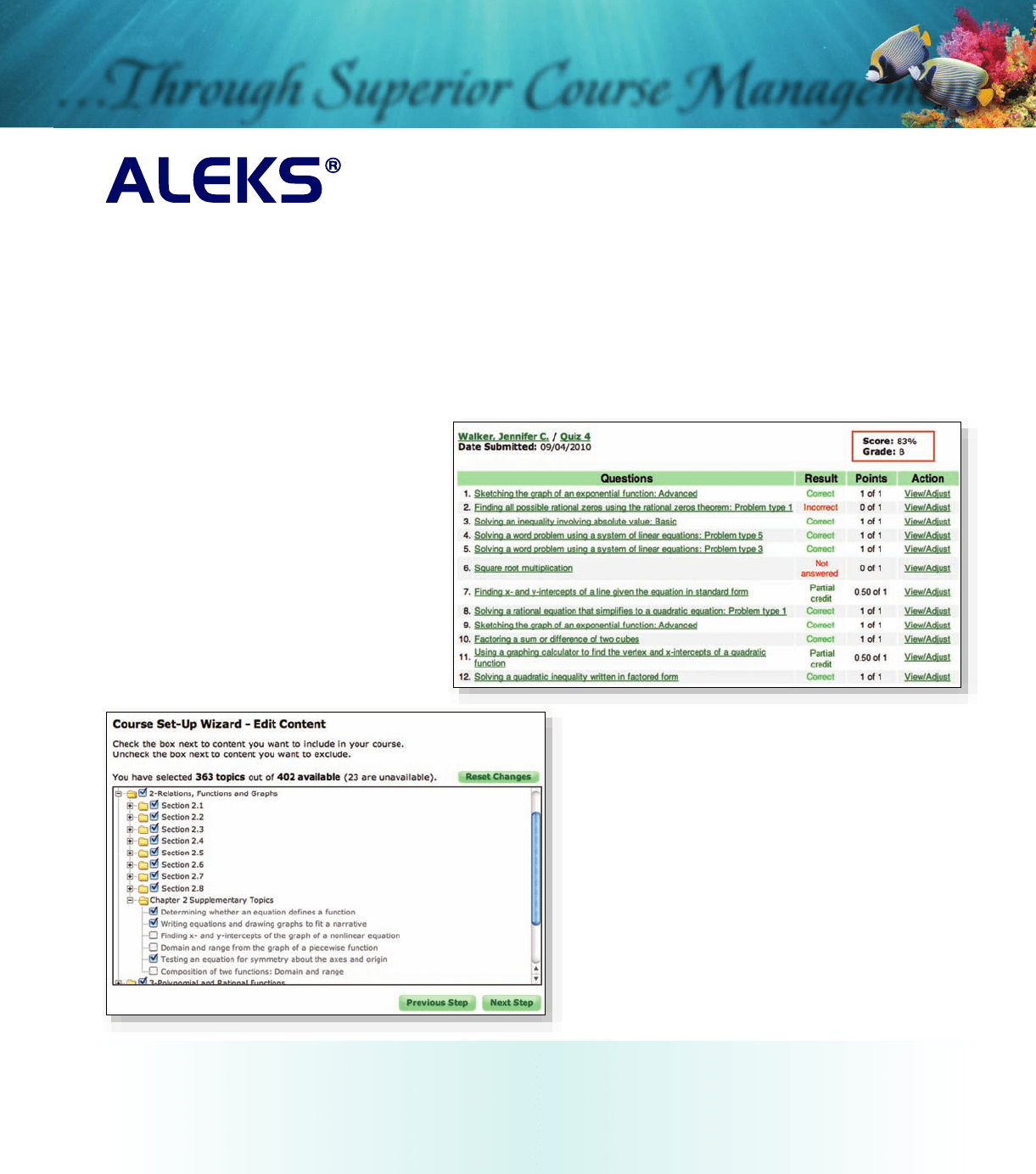
Partial Credit On Assignments: ▶
With the addition of many more multipart
questions to ALEKS College Algebra,
instructors now have the option to have
ALEKS automatically assign partial credit to
students’ responses on multipart questions
in an ALEKS Homework, Test, or Quiz.
Instructors can also manually adjust scores.
◀
Supplementary Textbook
Integration Topic Coverage:
Instructors have access to ALL course topics
in ALEKS College Algebra, and can include
supplementary course topics even if they are
not specifically tied to an integrated textbook’s
table of contents.
To learn more about how other instructors have
successfully implemented ALEKS, please visit:
www.aleks.com/highered/math/implementations
ALEKS includes an Instructor Module with powerful, assignment-driven features and extensive content flexibility to
simplify course management so instructors spend less time with administrative tasks and more time directing student
learning. The ALEKS Instructor Module also includes two new features that further simplify course management and
provide content flexibility: Partial Credit on Assignments and Supplementary Textbook Integration Topic Coverage.
For more information about ALEKS, please visit: www.aleks.com/highered/math
“ Overall, both students and I have been very pleased with ALEKS. Students like the flexibility
it offers them. I like that students are working where they need to be and can spend as much
time reviewing as they need. . . . Students have made such comments as ‘I never liked math
in high school but this is kind of fun,’ or ‘I never understood this in high school but now I do.’”
—Linda Flanery, Instructor, Sisseton Wahpeton College
cob19545_fm_i-xxxviii.indd Page xv 22/12/10 4:24 PM user-f467cob19545_fm_i-xxxviii.indd Page xv 22/12/10 4:24 PM user-f467 /Volume/204/MHDQ268/wea25324_disk1of1/0073525324/wea25324_pagefiles/Volume/204/MHDQ268/wea25324_disk1of1/0073525324/wea25324_pagefiles

Increased Student Engagement . . .
▶
Chapter Openers highlight Chapter Connections, an interesting
application exercise from the chapter, and provide a list of other
real-world connections to give context for students who wonder
how math relates to them.
▶
Examples throughout the text feature word problems, providing
students with a starting point for how to solve these types of
problems in their exercise sets.
Making mathematics meaningful requires that students experience a connection between the
mathematics they study, and its impact on the world they live in. This text is the result of a powerful
commitment to provide applications of the highest quality, and greatest interest, having close ties to the
examples, and with carefully monitored levels of difficulty. We particularly made an effort to supply
these in sufficient quantity to be used for in-class illustrations, included as homework assignments, and
employed in the construction of quizzes and tests, without exhausting their supply prematurely. Many
applications were born of our own diverse experiences, with others coming from a curious, even
visionary folly that enables one to seize on the everyday events of life, and to see the mathematics in
the background. These were supported by a substantial library of reference and research tools, with
an eye toward history, current events, and modern trends. —The Authors
▶
Application Exercises at the end of each section are the hallmark of
the Coburn series. Never contrived, always creative, and born out of
the author’s life and experiences, each application tells a story and
appeals to a variety of teaching styles, disciplines, backgrounds, and
interests. The authors have ensured that the applications reflect the
most common majors of college algebra students.
▶
Math in Action Applets, located online, enable students to work
collaboratively as they manipulate applets that apply mathematical
concepts in real-world contexts.
“
I think the book has very modern applications and quite a few
of them. The calculator instructions are very well done.
”
—Nezam Iraniparast, Western Kentucky University
▶
“
The students always want to know ‘When am I ever going to have
to use algebra anyway?’ Now it will not be hard for them to see for
themselves some REAL ways.
”
—Sally Haas, Angelina College
xvi
Throu
g
h Meanin
g
ful A
pp
lication
s
ggpp
More on Functions
CHAPTER OUTLINE
2.1 Analyzing the Graph of a Function 188
2.2 The Toolbox Functions and Transformations 202
2.3 Absolute Value Functions, Equations,
and Inequalities 218
2.4 Basic Rational Functions and Power Functions;
More on the Domain 230
2.5 Piecewise-Defined Functions 245
2.6 Variation: The Toolbox Functions in Action 259
CHAPTER CONNECTIONS
Viewing a function in terms of an equation, a
table of values, and the related graph, often
brings a clearer understanding of the
relationships involved. For example, the power
generated by a wind turbine is often modeled
by the function , where P is the
power in watts and v is the wind velocity in
miles per hour. While the formula enables us
to predict the power generated for a given wind
speed, the graph offers a visual representation
of this relationship, where we note a rapid
growth in power output as the wind speed
increases. This application appears as
Exercise 107 in Section 2.2.
Check out these other real-world connections:
䊳
Analyzing the Path of a Projectile
(Section 2.1, Exercise 57)
䊳
Altitude of the Jet Stream
(Section 2.3, Exercise 61)
䊳
Amusement Arcades
(Section 2.5, Exercise 42)
䊳
Volume of Phone Calls
(Section 2.6, Exercise 55)
P 1v2
8v
3
125
187
EXAMPLE 2
䊳
Identifying Functions
Two relations named f and g are given; f is pointwise-defined (stated as a set of
ordered pairs), while g is given as a set of plotted points. Determine whether each
is a function.
( ), and (6, 1)
Solution
䊳
The relation f is not a function, since is paired
with two different outputs: and .
The relation g shown in the figure is a function.
Each input corresponds to exactly one output,
otherwise one point would be directly above the
other and have the same first coordinate.
13, 2213, 02
3
4, 510, 12,f: 13, 02, 11, 42, 12, 52, 14, 22, 1 3, 2 2, 13, 6 2,
Now try Exercises 11 through 18
䊳
(4, 2)
(2, 1)
(1, 3)
(0, 5)
(4, 1)
(3, 1)
x
y
55
5
5
g
M
t
h
i
A
t
i
A
l
t
l
t
d
l
i
bl
t
d
t
t
k
“
The amount of technology is great, as are the applications.
The quality of the applications is better than my current text.
”
—Daniel Russow, Arizona Western College–Yuma
cob19545_fm_i-xxxviii.indd Page xvi 22/12/10 4:24 PM user-f467cob19545_fm_i-xxxviii.indd Page xvi 22/12/10 4:24 PM user-f467 /Volume/204/MHDQ268/wea25324_disk1of1/0073525324/wea25324_pagefiles/Volume/204/MHDQ268/wea25324_disk1of1/0073525324/wea25324_pagefiles
In mathematics, it would be difficult to overstate the importance of examples that set the stage
for learning. Not a few educational experiences have faltered due to an example that was too
difficult, a poor fit, out of sequence, or had a distracting result. In this series, a careful and
deliberate effort was made to select examples that were timely and clear, with a direct focus on
the concept or skill at hand. Everywhere possible, they were further designed to link previous
concepts to current ideas, and to lay the groundwork for concepts to come. As a trained educator
knows, the best time to answer a question is often before it’s ever asked, and a timely sequence of
carefully constructed examples can go a long way in this regard, making each new idea simply the
next logical, even anticipated step. When successful, the mathematical maturity of a student grows
in unnoticed increments, as though it was just supposed to be that way. —
The Authors
xvii
Through Timely Examples
▶
Side by side graphical and algebraic solutions illustrate the
difference between problem-solving methods, emphasize the
connections between algebraic and graphical information,
and enable students to understand why one method might be
preferable to another for any given problem.
▶
Titles have been added to examples to
highlight relevant learning objectives
and reinforce the importance of speaking
mathematically using vocabulary.
▶
Annotations located to the right of the
solution sequence help the student recognize
which property or procedure is being
applied.
▶
“Now Try” boxes immediately following
examples guide students to specific matched
exercises at the end of the section, helping
them identify exactly which homework
problems coincide with each discussed
concept.
Graphical Solution
䊳
The complete graph of g shown in Figure 3.30 confirms the analytical solution
(using the zeroes method). For the intervals of the domain shown in red:
, the graph of g is below the x-axis . The point (3, 0)
is on the x-axis . As with the analytical solution, the solution to this
“less than or equal to” inequality is all real numbers. A calculator check of the
original inequality is shown in Figure 3.31.
Now try Exercises 121 through 132
䊳
62
8
x
2
y
g
(x)
8
10
3
2
Figure 3.30
Figure 3.31
3g132 0 4
3g1x26 0 41q, 32 ´ 13, q2
Figure 3.29
WORTHY OF NOTE
Since was a zero of
multiplicity 2, the graph “bounced
off” the x-axis at this point, with no
change of sign for g. The graph is
entirely below the x-axis, except at
the vertex (3, 0).
x 3
EXAMPLE 8
䊳
Solving a Quadratic Inequality
Solve the inequality .
Analytical Solution
䊳
Begin by writing the inequality in standard form: . Note this is
equivalent to for . Since , the graph of g will
open downward. The factored form is , showing 3 is a zero and a
repeated root. Using the x-axis, we plot the point (3, 0) and visualize a parabola
opening downward through this point.
Figure 3.29 shows the graph is below the x-axis (outputs are negative) for all
values of x except . But since this is a less than or equal to inequality, the
solution is .
a 0
101234567
x
x 僆 ⺢
x 3
g1 x21x 32
2
a 6 0g1 x2x
2
6x 9g1 x2 0
x
2
6x 9 0
x
2
6x 9
“
The modeling and regression
examples in this text are excellent,
and the instructions for using the
graphing calculator to investigate
these types of problems are great.
”
—Allison Sutton, Austin
Community College
“
The authors have succeeded with numerous
calculator examples with easy-to-use instructions
to follow along. I truly enjoy seeing plenty of
calculator examples throughout the text!!
”
—David Bosworth, Huchinson Community College
Now
try
Exer
cis
e
s
121
thro
“
The examples support the exercises which is very
important. The chapter is very well written and is
easy to read and understand.
”
—Joseph Lloyd Harris, Gulf Coast Community College
cob19545_fm_i-xxxviii.indd Page xvii 22/12/10 4:25 PM user-f467cob19545_fm_i-xxxviii.indd Page xvii 22/12/10 4:25 PM user-f467 /Volume/204/MHDQ268/wea25324_disk1of1/0073525324/wea25324_pagefiles/Volume/204/MHDQ268/wea25324_disk1of1/0073525324/wea25324_pagefiles
